m法群桩基础整体刚度等代模拟分析

刘 润 舟

(南昌铁路勘测设计院有限责任公司，江西 南昌 330002)

m法群桩基础整体刚度等代模拟分析

刘 润 舟

(南昌铁路勘测设计院有限责任公司，江西 南昌 330002)

总结基于“m”法的单柱弹簧模型和双柱框架模型2种等代模拟群桩基础整体刚度的方法,对2种等代桩基模型进行比较分析，验证了等代模型的正确性，为类似工程提供参考。

群桩基础，整体刚度，等代模拟，m法

1 概述

多跨超静定桥梁结构有限元分析时，通常应建立上、下部结构的整体模型，并考虑群桩基础刚度的影响才能真实反映上、下部结构之间的相互作用。在铁路桥梁[1]和轨道交通高架桥[2]设计中均要求满足桥墩纵、横向线刚度[3]的要求，大跨度刚构桥及门式刚架结构墩、梁刚度合理分配，都必须先计算群桩基础整体刚度。

2 群桩基础整体刚度计算方法

现行桥涵设计规范推荐按m法计算弹性桩的位移和作用效应，其中，m为非岩石水平抗力系数的比例系数。非岩石地基的抗力系数随埋深成比例增大，深度z处的地基水平抗力系数Cz=m×z，而岩石地基的抗力系数不随岩层埋深变化，Cz=C0，为常数。

群桩基础中的单桩与土相互作用类似弹性地基梁，即土体反力和土体变形成比例，可以采用幂级数解法求单位水平力、单位竖向力和单位弯矩作用下的位移表达式，见图1。

等代模拟[4-6]就是在相同的外力作用下，使原结构和模拟结构具有相同的位移[7-9]，这样可以简化计算，避免建立复杂的桩体土体相互作用三维实体模型，又能满足工程设计精度要求。

首先由m法计算出承台底平面刚度系数：产生竖向单位位移时竖向反力之和rcc；产生水平单位位移时水平反力之和raa；产生单位转角位移时水平反力之和rαβ；产生单位转角位移时反弯矩之和rββ。由此可得相应柔度系数：竖向单位力时产生的竖向位移δPP；

水平单位力时产生的水平位移δHH；单位弯矩时产生的转角位移δMM；单位弯矩时产生的水平位移δMH。

2.1等代模型1：单柱弹簧模型

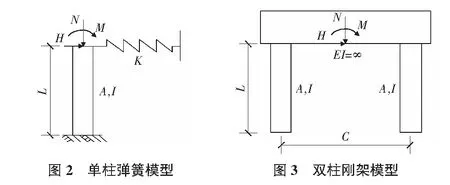
单柱弹簧模型是比较常用的等代模型，由刚度系数换算单柱长度L、截面高度h,截面宽度b及弹簧刚度K,将以上参数输入软件就可以等代群桩基础参与有限元分析，见图2。通过柔度系数换算上述参数，公式如下：

2.2等代模型2：双柱刚架模型

双柱刚架模型是另一种比较常用的等代模型，由刚度系数换算双柱长度L、柱截面惯性矩I、柱截面面积A、柱中心距C、高度h,截面宽度b及弹簧刚度K,将以上参数输入软件就可以等代群桩基础参与有限元分析,见图3。通过柔度系数换算上述参数，公式如下：

3 算例分析

某直线铁路桥梁下部结构采用4φ1.2 m钻孔灌注桩基础，桩长20 m，桩基中心距3.0 m，作用于承台底群桩基础重心处的荷载为竖向力N=12 000 kN，弯矩M=11 000 kNm，水平力H=600 kN，桩身采用C25混凝土，Ec=2.9×107kPa，地基土平均内摩擦角a=24°，桩侧地基系数的比例系数m=10 000 kPa/m2, 桩底地基系数的比例系数m0=30 000 kPa/m2。由以上参数计算可得单位力产生的单位位移，如表1所示。

表1 柔度系数表

以上柔度系数可以转化为刚度系数，相应刚度系数如下：

竖向刚度系数γcc=7 252 042.89 kN/m，水平刚度系数γaa=482 487.68 kN/m;

转动刚度系数γββ=21 321 754.67 kNm/rad，弯剪刚度系数γaβ=-1 219 052.63 kN/rad。

根据刚度系数或柔度系数，计算等代模型1和等代模型2的相关参数如表2所示。

表2 等代模型参数表

为验证等效模型的准确性，在Midas有限元分析软件中建立以上两个等代模型，分别采用等代模型法、节点刚度系数法进行计算，桥梁通辅助工具、桥梁博士基础设计工具，结果见表3，图4～图6。

表3 承台底位移计算结果

等代模拟法可以计算群桩基础整体刚度，进而计算承台底位移，但无法计算基础单桩的内力情况，而由规范编制的一些计算工具如桥梁通辅助计算工具只能计算出桩顶竖向力，桥梁博士可在计算承台底位移的同时计算基桩内力，如表4所示。

表4 基桩内力计算结果

模型最大桩顶轴力/kN桩顶剪力/kN桩顶弯矩/kNm规范法4865.915048.9桥梁通辅助工具4833.3——桥梁博士基础设计4868.615052.9

4 结语

基于“m”法模拟群桩基础整体刚度是群桩基础计算中的常用方法，文章对2种等代桩基模型进行比较分析，并验证了等代模型的正确性。运用等代模型法或承台底节点刚度系数法可以将群桩基础简化后输入有限元分析软件，和桥墩及梁体一同分析运算，充分体现了上部结构、下部结构及土的相互作用，广泛应用于桥墩线刚度计算、超静定结构的大跨度预应力连续刚构桥及预应力门式刚架墩等复杂结构计算中。

[1] TB 10093—2017,铁路桥涵地基与基础设计规范[S].

[2] 薛宇光.高架车站模拟分析[J].铁道勘测与设计,2010(4):62-66.

[3] TB 10093—2017，铁路无缝线路设计规范[S].

[4] 鲍卫刚，谌启发.虎跳门大桥桩基等效模拟计算[J].桥梁建设,2000(1):69-71.

[5] 杜振华.桥梁群桩基础的等代模拟及有限元分析[J].科技创新与应用,2015(11):12-13.

[6] 程翔云.群桩基础等代模型的改善[J].公路,2006(1):13-15.

[7] 鲍卫刚.桥梁承台桩基柔度的模拟[J].华东公路,1992(5):16-17.

[8] 刘祚秋.桩、土、刚性承台相互作用下桩基内力计算新方法[J].中山大学学报,2004(4):33-37.

[9] 李 杰，朱 勤.桩基等代计算中的比拟杆件法[J].中外公路,2002(4):44-46.

Equivalentanalysisofintegralstiffnessofpilegroupfoundationbasedon“m”method

LiuRunzhou

(NanchangRailwaySurveyandDesignInstituteCo.,Ltd,Nanchang330002,China)

Summary of integral stiffness of pile group foundation based on “m” method, comparison of two similar models, such as single column spring model and two column frame model. The theoretical models have testified their validity, provide a reference for the similar projects concerned.

pile group foundation, integral stiffness, equivalent similation, “m” method

U445.551

A

1009-6825(2017)27-0136-02

2017-07-17

刘润舟(1982- )，男，高级工程师