基于分数时延信道模型的低复杂度信道估计方法
2017-11-01马子骥周冰航李元良
马子骥,彭 强,周冰航,李元良,唐 涛
(湖南大学 电气与信息工程学院,长沙 410082)

基于分数时延信道模型的低复杂度信道估计方法
马子骥,彭 强,周冰航,李元良,唐 涛
(湖南大学 电气与信息工程学院,长沙 410082)
由于多载波系统无线信道固有的稀疏特性,压缩感知技术(compressed sensing, CS)已被应用于正交频分复用(orthogonal frequency division multiplexing,OFDM)系统的信道估计中以提高频谱利用率。然而,传统的时域普通采样方法会导致信道恢复字典不够精细,无法精确反映传输信道路径特性。针对这一问题,提出采用多径稀疏分数时延信道模型来模拟OFDM系统的无线多径信道,利用在接收端进行时域过采样方法细化信道恢复字典以提高信道估计精度。同时,针对过采样引起的压缩感知测量矩阵的扩大而导致重构算法的复杂度增加的问题提出采用广义正交匹配追踪算法(generalized orthogonal matching pursuit,GOMP)以降低计算复杂度。仿真结果表明接收端时域过采样方法能准确检测到信道的分数时延且采用的GOMP算法能将传统的OMP算法的复杂度降低近80%,验证了所采用的信道估计方法的可靠性和有效性。
压缩感知;匹配追踪;分数时延;过采样
0 引 言
正交频分复用(orthogonal frequency division multiplexing,OFDM)系统是一种多载波系统,每一个载波具有较低符号率[1]。研究表明散射环境下OFDM系统无线信道在信号空间维度上呈现出“稀疏”特性,其多径信道由多条路径组成,但只有少数路径占据大部分发送功率[2-3],针对这一特点,压缩感知(compressed sensing,CS)技术已被应用于OFDM系统信道估计中,它是一种能用较少的测量开销去估计稀疏信号的技术[4]。传统的OFDM系统信道估计方法大都基于信道多径时延为整数倍采样周期这一理想情况进行。然而,现实环境中,各传输路径的延时不可能恰巧为采样周期的整数倍,这一现象可称之为分数时延,而这将直接影响信道估计的精度。文献[5-7]中提到了各种基于压缩感知的信道估计方法。然而分数时延的问题并未得到重视,这些方法在信道环境恶劣的情况下都有较为明显的性能下限。文献[8-10]证明了在时域利用过采样可以得到信道路径分数时延特性。根据文献[11],基于压缩感知的信道估计充分利用了信道冲激响应的时域稀疏特性,表明若路径最大时延不超出保护间隔,则在时域进行信道估计可以取得比常见的频域信道估计更高的精度。文献[12-13]研究了在多径衰落信道中采用过采样估计信道的时延特性,表明通过过采样方法得到多径时延特性可以改善信道估计性能。然而文献[12-13]采用了在发送端进行过采样的策略,需增加额外的发送带宽。另一方面,基于压缩感知的信道估计算法在近几年获得了极大的关注,其中较为知名的算法有:基于L1范数最小化的基追踪(basis pursuit, BP)算法[14]、基于贪婪迭代的匹配追踪(matching pursuit, MP)算法和正交匹配追踪(orthogonal matching pursuit, OMP)算法[15-16]等。其中OMP算法具有重构精度高,计算速度快的优点。目前已经出现的基于CS的信道估计算法,信道恢复的精度已经能够达到较高的水平。然而,传统的CS求解算法需要反复迭代计算,居高不下的算法复杂度问题是其推广应用的较大障碍。
本文致力于研究信道的分数时延特性,通过在接收端进行过采样以获取多径的分数时延。以典型城市6径信道(typical urban 6,TU6)为例,进一步研究在多径传输环境下的信道估计。本文采用的信道估计方法是一种基于压缩感知的信道估计方法,在计及更为一般的信道路径分数时延模型,为了准确检测到分数时延,与文献[12-13]在发送端与接收端都进行过采样不同,本文仅在接收端进行过采样,无需增加额外的发送带宽。同时,为了克服由于过采样而引起的压缩感知测量矩阵的扩大而导致重构算法的复杂度增加的问题,在不牺牲信道估计性能的前提下,采用广义正交匹配追踪算法(generalized orthogonal matching pursuit,GOMP)进行稀疏信号重构[17]。GOMP 算法是一种OMP算法的改进算法,它通过降低OMP算法的迭代次数以降低计算复杂度。

1 系统模型
用来仿真的系统框图如图1所示。

图1 系统框图Fig.1 System block diagram
发送信号U含K个有效子载波信号,其中包含M个导频符号和K-M个数据符号,表示为
U=[U0,U1,…,UK-1]T
(1)
(1)式中,U的每一项为
(2)
(2)式中:pm为第m个导频符号;dk是第k个数据符号;C=K/M为导频间隔。
快速傅里叶变换(fast Fourier transformation,FFT)矩阵F为
(3)
重排矩阵Q为
(4)
重排矩阵用于重新排列有效子载波的正频率和负频率部分,由K×K的单位阵IK和零矩阵Z组成。K+和K-分别为正频率和负频率子载波数目。
信号U与重排矩阵Q以及FFT逆矩阵F-1相乘后得到OFDM符号s
s=F-1QU
(5)
s添加循环前缀(cyclic prefix,CP)后,再经过转换周期为Ts的数模转换器形成基带传输信号。最后经过上变频调制后经加性高斯白噪声多径信道发送到接收端。
在接收端,接收信号r(t)为
(6)
(6)式中:hl和τl分别表示第l条传播路径的路径损耗和时延;n(t)为加性高斯白噪声。
r(t)通过一个截止频率为Ts/2的低通滤波器进行滤波,随后再经过一个采样频率为1/Ts的模数转换器,最后去除信号的CP。去除CP后的接收信号r为
r=Gs+n
(7)
(7)式中:G和n分别为时域信道矩阵和时域加性高斯白噪声。
接收端的处理是发送端处理的逆过程,采用与发送端相同的FFT矩阵F和重排矩阵QT。接收信号V为
V=QTFr=QTLQU+N
(8)
(8)式中:L=FGF-1=diag(H)是对角矩阵,对角元素为信道频率响应H=[H0,H1,…,HN-1]T,N=QTFn为频域加性高斯白噪声。由此可以得到信道频率响应为
(9)
(10)
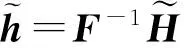

2 基于压缩感知的信道估计
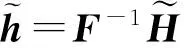
图2为本文采用的信道估计方法流程图。
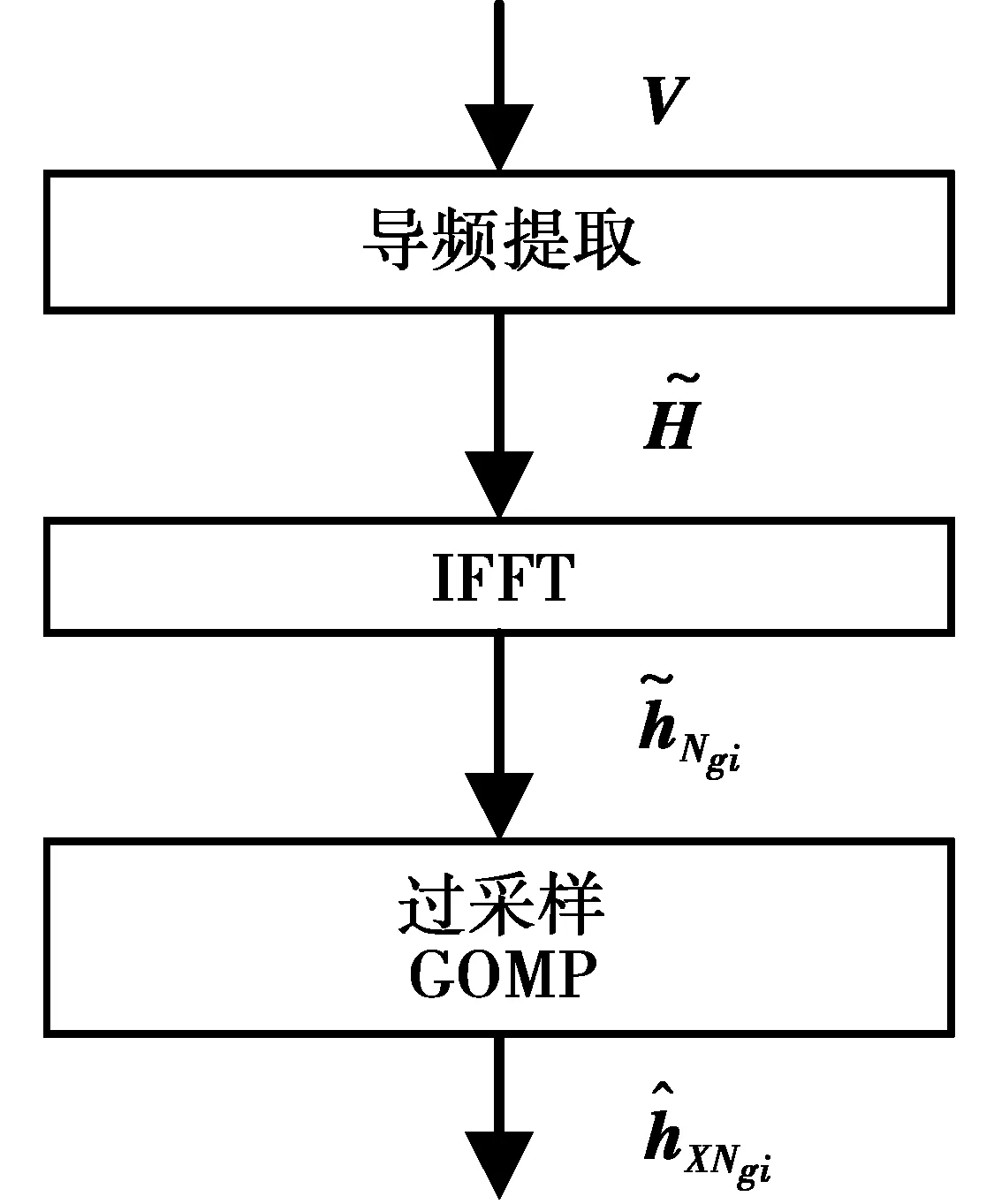
图2 信道冲激响应估计Fig.2 Proposed impulse response estimation

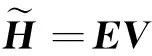
(11)
(11)式中,E是导频提取矩阵以提取接收导频。
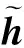
(12)

定义过采样因子X为信号的过采样的倍数,FX和QX分别为FFT矩阵F和重排矩阵Q扩大为X倍的矩阵,则频率响应HXN可以从冲激响应hXN=[h0,h1,…,hXN-1]T计算获得
(13)
(13)式中:Qs为导频抽取矩阵,其包含导频结构以提取接收导频处的信道频率响应,nXN为XN维的加性高斯白噪声。
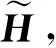
(14)
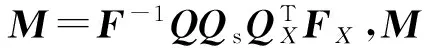
(15)
信道最大传播时延不超过保护间隔Ngi,相应地,过采样冲激响应可缩小为
hXNgi=[h0,h1,…,hXNgi-1]T
(16)
相应地,测量矩阵缩小为
MNgi,XNgi=[Mi,n]0≤i (17) (18) 图3是保护间隔为1/8,过采样因子X=1的不同大小FFT矩阵下得到的测量矩阵,表明随着FFT矩阵的增大测量矩阵变得更稀疏。由于在OFDM系统中采用的FFT矩阵很大,所以用于本文的测量矩阵非常稀疏。将稀疏测量矩阵用于压缩感知能够降低基于压缩感知的重构算法的计算开销[18]。 图3 不同大小FFT矩阵下的测量矩阵Fig.3 Measurement matrix for different FFT size 3.1 基于GOMP算法的信道估计 为解决OMP算法收敛慢,计算复杂度高的缺点,本文采用GOMP算法进行稀疏信道估计。GOMP算法的具体实现如下。 3)假设已迭代了i-1次,对于第i次迭代: 步骤1识别:取e=MNgi,XNgiri-1中前n个最大值的索引集en。 步骤2合并:di=di-1∪en,将测量矩阵中对应的列向量并入原子集中:Yi=[Yi-1,Men]。 步骤5判断:若i≥η或‖ri‖2<σ2,则停止迭代,反之则令i=i+1,返回步骤1。 与OMP算法不同,GOMP算法在每次迭代时从MNgi,XNgiri-1中选取前n(n≥1)个最大值的索引值,再利用选取的原子进行估计和残差更新,利用索引集加快算法收敛,进而降低算法的计算复杂度。因此一般情况下算法迭代η/n次即可完成原稀疏信道的精确重建,这大大缩短了运行时间。关于n的取值,给出引理1。 引理1在GOMP算法中,假设每次迭代选择n个原子,则当n满足(19)式所示的关系时,GOMP算法可以实现原稀疏信道的重建[17]。 (19) (19)式中:η和M分别为信道的稀疏度和导频的个数。 3.2 计算复杂度分析 本节分析GOMP算法的计算复杂度,在第2章中,观测冲激响应向量的维数从N缩小到了保护间隔长度。例如,如果保护间隔为1/8,则该向量维数减少了87.5%。根据3.1节,压缩感知重构算法需对测量矩阵的列向量和残差进行内积计算,而测量矩阵的列向量是稀疏的,矩阵的大部分元素为0,这能大大降低算法的计算复杂度。此外,本文采用的GOMP算法是一种低复杂度算法,它能进一步降低算法的计算复杂度。 OMP算法每一次迭代得到一个残差r和测量矩阵MNgi,XNgi的内积,其计算量为O(X(Ngi)2)。OMP算法中使用了最小二乘(least square,LS)算法,其计算量为O(η2Ngi)。OMP总的计算量为 O(ηNgi(XNgi+η2)) (20) (20)式中:Ngi为保护间隔长度;X为过采样因子;η为稀疏度。 而GOMP的计算量为 O((η/n)Ngi(XNgi+η2)) (21) 为了更形象地对比计算复杂度,举例说明:设发送了10个OFDM符号,η=6,Ngi=64,n=5,X=2。OMP算法计算量利用(20)式算得:10×(6×64×(2×64+62))=629 760。利用(21)式算得GOMP算法的计算量:10×((6/5)×64×(2×64+62))=125 952。比较这2种算法的计算量GOMP算法相比OMP算法节省的计算开销为 (22) 本章进行仿真结果分析,采用的评估指标为误比特率 (bit error rate,BER),同时分析了计算复杂度。表1为仿真采用的信道模型[19]参数,表2为采用的系统仿真参数。 表1 TU6信道参数 注:1)0.05 μs为添加的路径分数时延,不加0.05 μs时对应整数时延信道。 表2 仿真参数 注:1)X为过采样因子,确定过采样倍数。 4.1 误比特率分析 图4为TU6整数时延信道估计的BER性能,表明在信道路径时延为整数时延的情况下,采用过采样的OMP算法和GOMP算法与采用普通采样的OMP算法和GOMP算法信道估计都保持较好的BER性能。图5为TU6分数时延信道估计的BER性能,分数时延为0.05 μs,令所有信道路径分数时延均为0.05 μs,如果进行普通采样,采样点将会偏移0.05 μs。图5显示采用普通采样的OMP算法和GOMP算法均存在较高的BER,这是因为信道存在分数时延。为了检测0.05 μs的分数时延,在接收端进行过采样,令过采样因子X为普通采样的2倍,从图5中可见采用过采样的OMP算法和GOMP算法均可以得到更佳的BER性能。 图4 TU6整数时延误比特率Fig.4 BER in TU6 Integer delay channel 图5 TU6信道分数时延误比特率Fig.5 BER in TU6 fractional delay channel 4.2 算法复杂度对比 图6对比了在不同过采样因子X下OMP算法与GOMP算法的计算量。表明随着过采样因子X的增加,OMP算法和GOMP算法的计算量都在增加。但GOMP算法相比传统的OMP算法计算量更小。 图6 计算量对比Fig.6 Computational complexity comparison 系统仿真环境:内存8G,CPU型号为i3-4160,主频3.6 GHz,matlab2011b。在分数时延信道模型下,算法的时间复杂度对比如表3,由表3可知,在过采样因子X=1的情况下,GOMP算法比OMP算法节省了约79%的时间,在过采样因子X=2的情况下,GOMP算法比OMP算法节省了约80%的时间,这与3.2节中分析的算法理论计算量是一致的。 表3 时间复杂度对比 本文在引入多径分数时延信道模型的基础上,采用接收端过采样技术,实现了基于压缩感知算法的稀疏信道估计。由于过采样仅仅在接收端进行,有效地避免了传输带宽的增加,即无需额外提高发送功率。由此实现了信道恢复字典的精细化,提高了在多径分数时延情况下的信道估计精度。再结合GOMP算法,能够在不牺牲已获得优势的情况下,相比于传统的OMP算法,将算法的计算复杂度降低了近80%。 [1] WEINSTEIN S B, EBERT P M. Data transmission by frequency division multiplexing using the discrete Fourier transform [J]. IEEE Transactions on Communication Technology, 1971, 19(5): 628-634. [2] VUOKKO L, KOLMONEN V M, SALO J, et al. Measurement of large-scale cluster power characteristics for geometric channel models [J]. IEEE Transactions on Antennas and Propagation, 2007, 55(11): 3361-3365. [3] BAJWA W U, HAUPT J, SAYEED A M, et al. Compressed Channel Sensing: A new approach to estimating sparse multipath channels [J].Proceedings of the IEEE, 2010, 98(6): 1058-1076. [4] DONOHO D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [5] MA Z J, LIU H L, HIGASHINO T, et al. Low-Complexity channel estimation for ISDB-T over doubly-selective fading channels [C]//Intelligent Signal Processing and Communications Systems (ISPACS), 2013 International Symposium on. Naha, Okinawa, Japan: IEEE, 2013: 114-118. [6] GYUU S, MA Z J, OKADA M. Low complexity channel estimation based on compressed sensing for OFDM system [C]//2013 International Conference on Embedded Systems and Intelligent Technology. Nong Khai, Thailand: IEICE, 2013: 55-58. [7] 王东梅,候晓赟.非整数倍路径时延下的OMP信道估计方法 [J].电路与系统学报,2013, 18(1): 304-309。 WANG Dongmei, HOU Xiaoyun. OMP channel estimation method for non-integer multipath delay environment [J].Journal of circuits and systems, 2013, 18(1): 304-309. [8] TEPEDELENLIOGLU C, CHALLAGULLA R. Low-complexity multipath diversity through fractional sampling in OFDM [J]. IEEE Transactions on Signal Processing, 2004, 52(11): 3104-3116. [9] WU J X, ZHENG Y R. Oversampled orthogonal frequency division multiplexing in doubly selective fading channels [J]. IEEE Transactions on Communications, 2011, 59(3): 815-822. [10] PENG B, ROSSI S P, DONG H F, et al. Time-domain oversampled OFDM communication in doubly-selective underwater acoustic channels [J]. IEEE Communications Letters, 2015, 19(6): 1081-1084. [11] HAYASHI K, SAKAI M, KAMENOSONO T, et al. Compressed sensing based channel estimation for uplink OFDMA systems [C]//Signal and Information Processing Association Annual Summit and Conference. Klong Luang, Pathumthani, Thailand: IEEE, 2014: 1-7. [12] PADERNA R, HIGASHINO T, OKADA M, et al. Modified orthogonal matching pursuit based ISDB-T channel estimation over fractional delay channel [C]//Communications and Information Technologies(ISCIT), 2014 14th International Symposium on. Incheon, Korea: IEEE, 2014: 336-340. [13] PADERNA R, HIGASHINO T, OKADA M. Improved channel estimation for ISDB-T using modified orthogonal matching pursuit over fractional delay TU6 channel [C]//Signal and Information Processing Association Annual Summit and Conference(APSIPA), 2014 Asia-Pacific. Klong Luang, Pathumthani, Thailand: IEEE, 2014:1-5. [14] HUANG J Z, BERGER C R, ZHOU S L, et al. Comparison of basis pursuit algorithms for sparse channel estimation in underwater acoustic OFDM [C]// OCEANS 2010. Sydney, Australia: IEEE, 2010:1-6.2010:1-6. [15] SUN T, SONG Z Q, ZHANG Y J. Matching pursuit based sparse channel estimation using pseudorandom sequences [C]// 2012 5th Global Symposium on Millimeter Waves (GSMM). Harbin, China: IEEE, 2012: 33-37. [16] ABOUTORAB N, HARDJAWANA W, VUCETIC B. Application of compressive sensing to channel estimation of high mobility OFDM systems [C]// 2013 IEEE International Conference on Communications(ICC). Budapest, Hungary: IEEE, 2013: 4946-4950. [17] WANG J, KWON S, SHIM B. Generalized orthogonal matching pursuit [J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6202-6216. [18] PADERNA R, HIGASHINO T, OKADA M. Reduced-complexity channel estimation for ISDB-T one-seg using modified orthogonal matching pursuit [C]// International Conference On Advances In Computer Science and Electronics Engineering (CSEE), New Delhi, India: IEICE, 2014: 167-171. [19] European Telecommunications Standards Institute (ETSI). TS 102 831 V1.2.1, Digital Video Broadcasting (DVB); Implementation guidelines for a second generation digital terrestrial television broadcasting system(DVB-T2)[EB/OL]. [2016-09-20]. http://www.etsi.org/deliver/etsi_ts/102800_102899/102831/01.02.01_60/ts_102831v010201p.pdf. (编辑:张 诚) Lowcomplexitychannelestimationmethodbasedonfractionaldelaychannelmodel MA Ziji, PENG Qiang, ZHOU Binghang, LI Yuanliang, TANG Tao (School of Electrical and Information Engineering, Hunan University, Changsha 410082, P.R. China) Due to the inherent sparse feature of the wireless channel in multi-carrier system, compressed sensing techniques are applied in the channel estimation of the OFDM system to improve spectrum utilization. However, the conventional time-domain sampling method causes the imprecision to the channel recovery dictionary, which can’t accurately reflect the characteristics of the transmission channel path. To solve this problem, a multipath sparse fractional delay channel model is used to simulate the OFDM wireless multipath channel. In addition, a time-domain oversampling based generalized orthogonal matching pursuit (GOMP) algorithm at the receiver is exploited to improve the estimation accuracy and keep a relatively low computational complexity which is increased due to the time-domain oversampling. Simulation results demonstrate that the time-domain oversampling can effectively detect the fractional delay. In contrast to the conventional OMP algorithm, the GOMP algorithm reduces the computational complexity by 80%. Hence, it verifies the reliability and the validity of the proposed method in this paper. compressed sensing; matching pursuit; fractional delay; oversampling s:The Central State-Owned Capital Management and Budget Project ([2013] 470);The Fundamental Research Funds for the Central Universities(2014-004);The National Nature Science Foundation of China (61540012);The National Doctoral Fund of China (2014M562100);The Hunan Provincial Science and Technology Department Funds (2015JC3053);The Ministry of Education Cooperative Education Project(201601004010) TN911.7 A 1673-825X(2017)05-0611-07 马子骥(1978-),男,湖南人,博士,讲师。主要研究方向为无线通信技术、数字信号处理。E-mail:zijima@hnu.edu.cn 彭 强(1989-),男,湖南人,硕士研究生。主要研究方向为无线通信。E-mail:perry@hnu.edu.cn 周冰航(1973-),男,湖南人,硕士,工程师。主要研究方向为嵌入式与信息处理。E-mail:hn_zhoubh@qq.com 李元良(1970-),男,湖南人,硕士,讲师。主要研究方向为数字信号处理。E-mail:16744301@qq.com 唐 涛(1991-),男,湖南人,硕士研究生。主要研究方向为数字信号处理。E-mail:tangtao911014@163.com。 2016-10-13 2017-05-05 马子骥 zijima@hnu.edu.cn 中央国有资本经营预算项目([2013]470号);中央高校基本科研项目(2014-004);国家自然科学基金(61540012);中国博士后科研基金(2014M562100);湖南省科技计划重点项目(2015JC3053);教育部产学合作协同育人项目(201601004010) 10.3979/j.issn.1673-825X.2017.05.006

3 GOMP算法与算法复杂度分析


4 仿真与分析


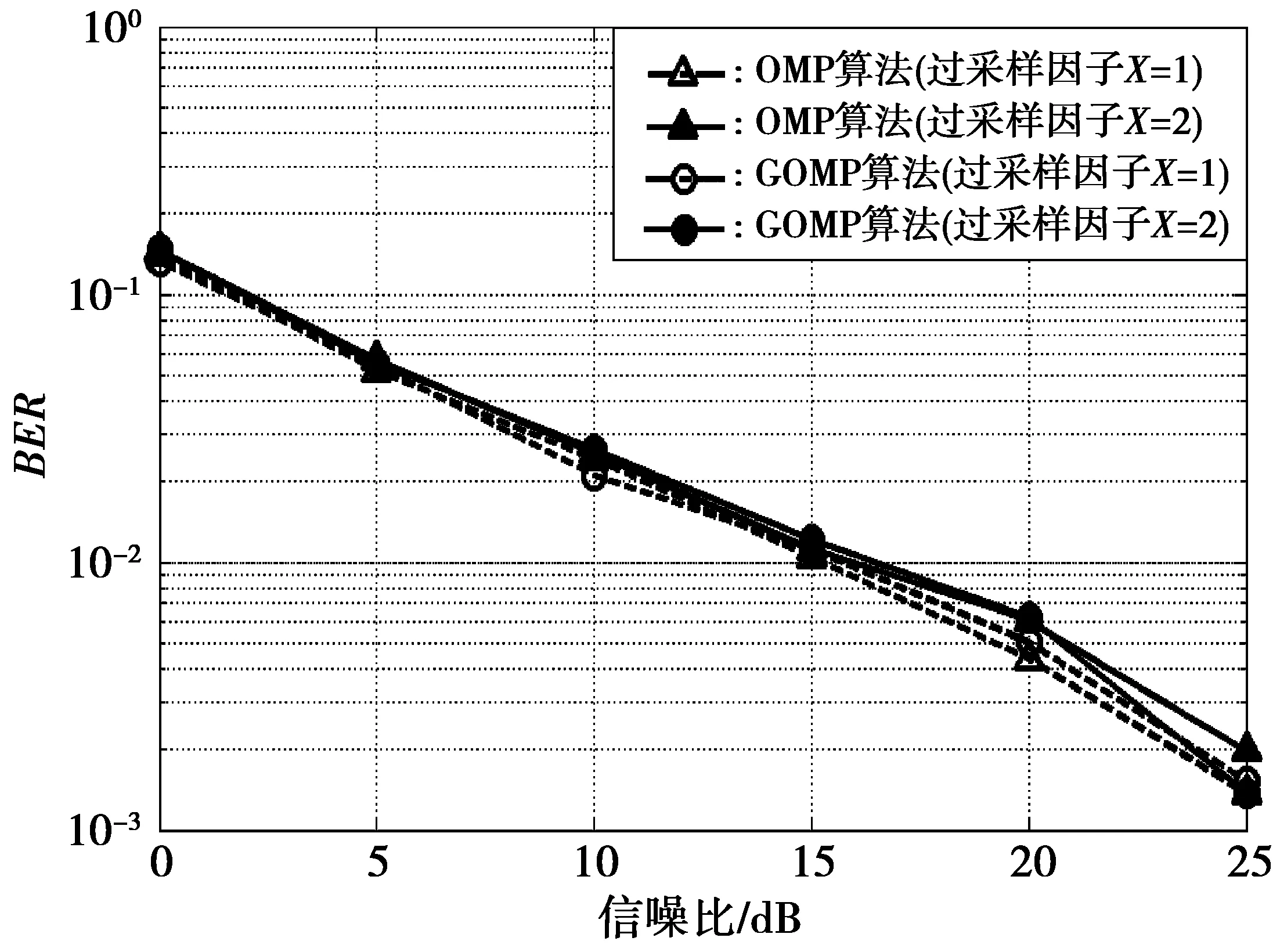
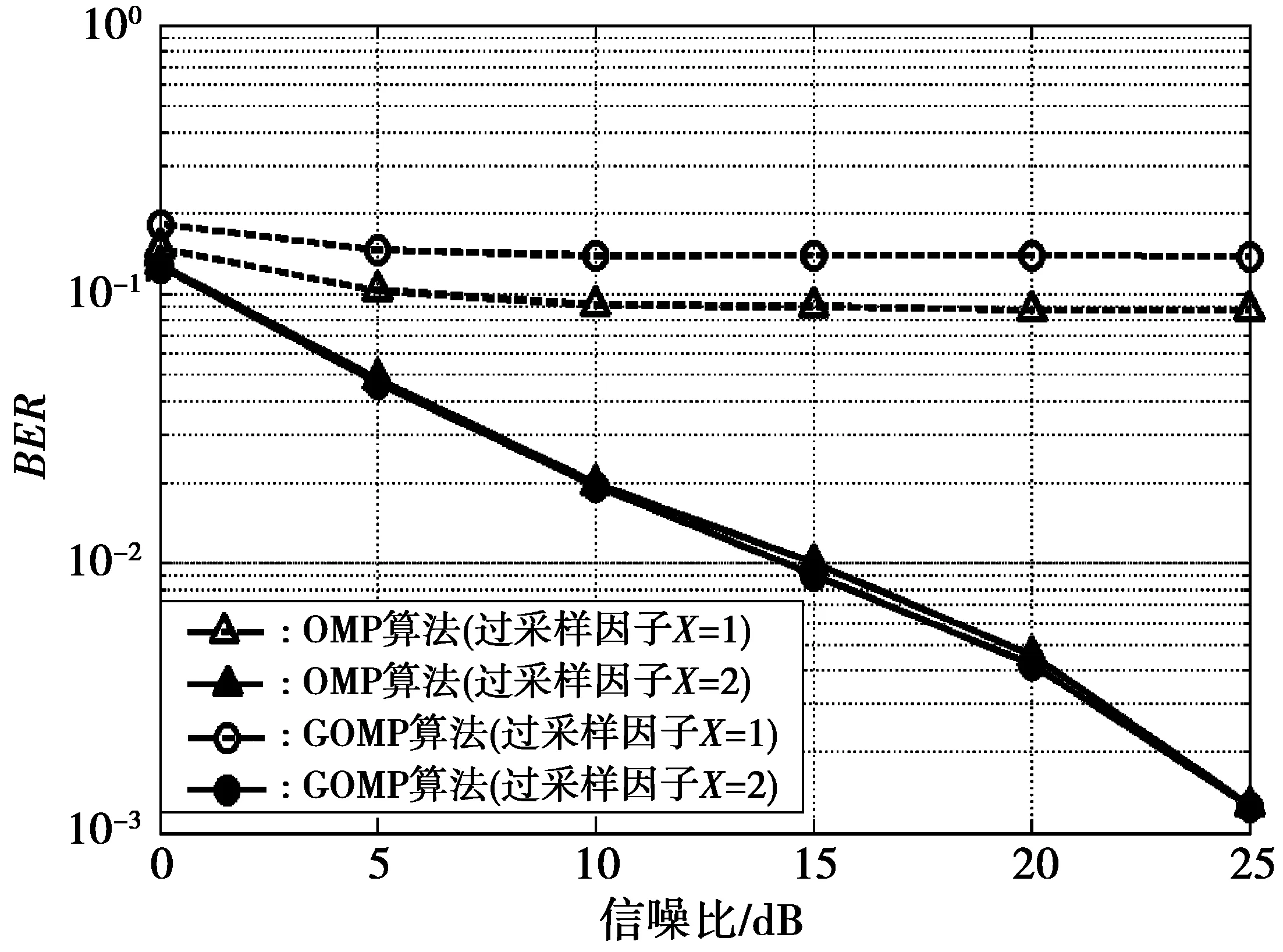


5 总 结





