大规模MIMO系统中基于空时相关性的导频减小算法
2017-11-01张进彦尹礼欣
金 凤,张进彦,尹礼欣
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)

大规模MIMO系统中基于空时相关性的导频减小算法
金 凤,张进彦,尹礼欣
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
在大规模多输入多输出(multiple input multiple output,MIMO)系统信道估计过程中,基站向用户端发送导频信号。由于导频数量与基站发射天线的数量成正比,传统信道估计过程会产生巨大的导频开销,尤其是对于采用频分双工通信方式的 (frequency-division duplexing,FDD)大规模MIMO系统。为了解决这一问题,通过利用无线MIMO信道的空间公共稀疏性和时间相关性,提出一种基于压缩感知(compressed sensing,CS)技术的导频开销减小算法,其中,空时相关性用来提高信道估计精度。该算法能够在未知大规模MIMO系统信道稀疏度的情况下,自适应地获取精确的信道状态信息。分析和仿真结果表明提出的算法在减少导频开销方面优于局部公共支撑算法,同时能够维持良好的信道估计性能。
大规模多输入多输出;空时相关性;信道估计;压缩感知
0 引 言
大规模MIMO(multiple input multiple output)技术作为5G通信的关键技术,具有显著的优势来提高无线系统的容量和可靠性。通过在基站端部署大规模天线,大规模MIMO系统可以极大地增强频谱效率与能量效率[1]。
在大规模MIMO系统中,精确的信道状态信息(channel state information, CSI)的获取对于下行信道波束复用、资源分配以及信号处理等起着尤为重要的作用。然而,由于基站端具有大规模天线,每个用户需要根据成百上千的发射天线来对信道进行估计,这导致了高比例的导频开销[2]。因此,如何选择一种合理有效的方式来减小导频开销是下一代绿色无线通信系统最具挑战的问题。为了减小信道估计开销,许多研究采用时分双工(time-division duplexing,TDD)通信方式[3]。在TDD通信中,由于用户数量较少以及基站强大的信号处理能力,利用信道互易性可以直接从上行信道的测量结果中推断出下行信道状态信息。然而,由于相邻小区需要复用有限的正交导频,TDD通信方式会出现严重的导频污染问题。与TDD系统相比,频分双工(frequency-division duplexing,FDD)大规模MIMO系统具有低迟延和对称通信量的优势[4],并且它目前已经广泛应用于无线通信系统。因此,本文利用FDD系统来实现对下行大规模MIMO信道估计的研究。
本文考虑的是瑞利衰落的大规模MIMO- OFDM(multiple-input multiple-output-orthogonal frequency division multiplexing)系统信道模型。传统MIMO系统配备很少的发射天线,因此导频开销不是严重的问题。但是对于FDD通信方式的大规模MIMO系统来说是不切实际的,因为基站端配备了大量的天线。因此,我们需要结合大规模MIMO-OFDM系统的性能提出一种合理的信道估计方式来减小导频开销。通常情况下,基站会架设在很高的位置,基站端具有有限的局部散射,并且随着基站天线数的增多,信道往往表现出稀疏性[5]。因此,利用信道的稀疏性,将压缩感知(compressed sensing,CS)理论应用到大规模MIMO信道估计中成为目前很受欢迎的一种技术。事实上,许多文献已应用CS技术来改善信道估计的性能[6-9]。例如,文献[7]提出一种基于CS技术的低阶矩阵近似算法来提高TDD通信方式下大规模MIMO系统信道估计性能,但是该理论不适用于FDD系统。文献[8]依据FDD通信方式下大规模MIMO系统信道的时间相关性和稀疏性提出一种减小导频开销的方式,但是随着发射天线数量的增多,不同发射天线的导频序列的干扰消除将会很困难。文献[9]利用连续信道脉冲响应(channel impulse response, CIR)的公共支撑集提出一种新颖的适用于大规模MIMO系统的稀疏信道估计机制,但是该文献只考虑了一个发射接收天线对的情况,并且算法中使用支撑向量来确定CIR向量中非零元素的位置,很大程度上加剧了信道估计复杂度。
针对FDD通信方式下的大规模MIMO系统,本篇论文联合利用大规模MIMO信道的时间相关性和公共稀疏性提出了一种基于CS技术的低导频开销信道估计方式。在下行信道,基站向用户端发射随机导频信号,用户根据接收的导频信号对大规模MIMO信道进行估计,并将最终估计结果反馈给基站。在用户端,联合利用大规模MIMO信道的空时相关性,本文设计了一种信道估计算法,通过该算法可以获取CIR向量的公共稀疏支撑集,进而实现低导频开销的信道估计。仿真结果证实与传统算法相比,提出算法可以在大大减小导频开销的同时维持很强的信道估计性能。
1 系统模型
1.1 联合空时相关性的大规模MIMO信道
研究表明,时域无线宽带信道通常表现出稀疏性。由于无线信道多径传播的特点, CIR向量通常具有稀疏性,即CIR向量系数接近于零的元素或数值为零的元素相对较多。不同发射接收天线对的CIR向量具有相似的路径延迟[10],因此不同发射接收天线对表现出空间相关性,可用公式表示为
sup(g1,n)=sup(g2,n)=…=sup(gM,n)
(1)
(1)式中:M为基站端发射天线数;n为OFDM符号下标数;gm,n表示第m个发射天线和一个用户间的时域CIR向量;sup(gm,n)表示gm,n的稀疏支撑集。通常路径延迟比路径增益慢得多[11],因此时域CIR向量中非零元素的位置变化很慢可近似为常数。也就是说,相邻L个OFDM信号具有公共稀疏性,可表示为
(2)
由(1)式和(2)式可知,对于L个连续的OFDM信号,无线MIMO信道表现出空间公共稀疏性和时间相关性。本文联合利用信道的空时相关性来设计FDD大规模信道估计算法以减小导频开销。
1.2 大规模MIMO系统
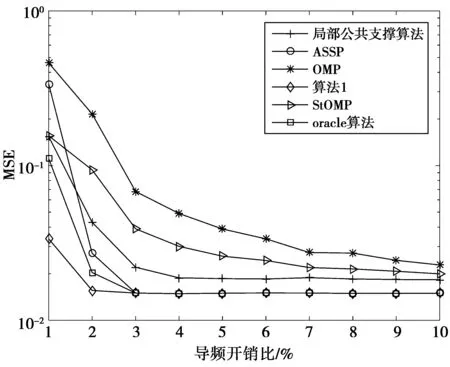
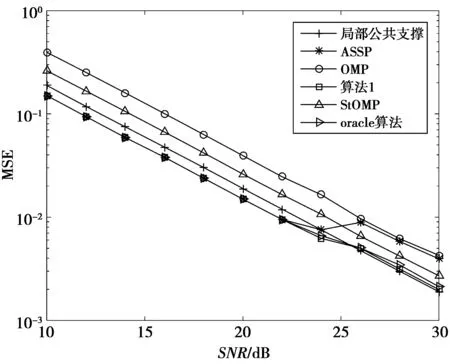
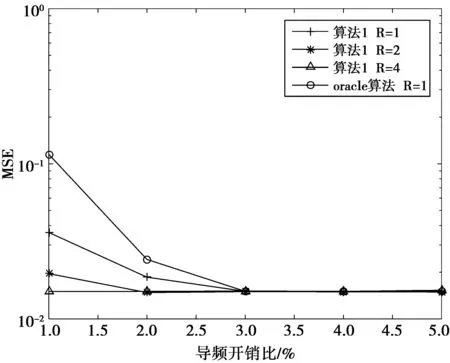
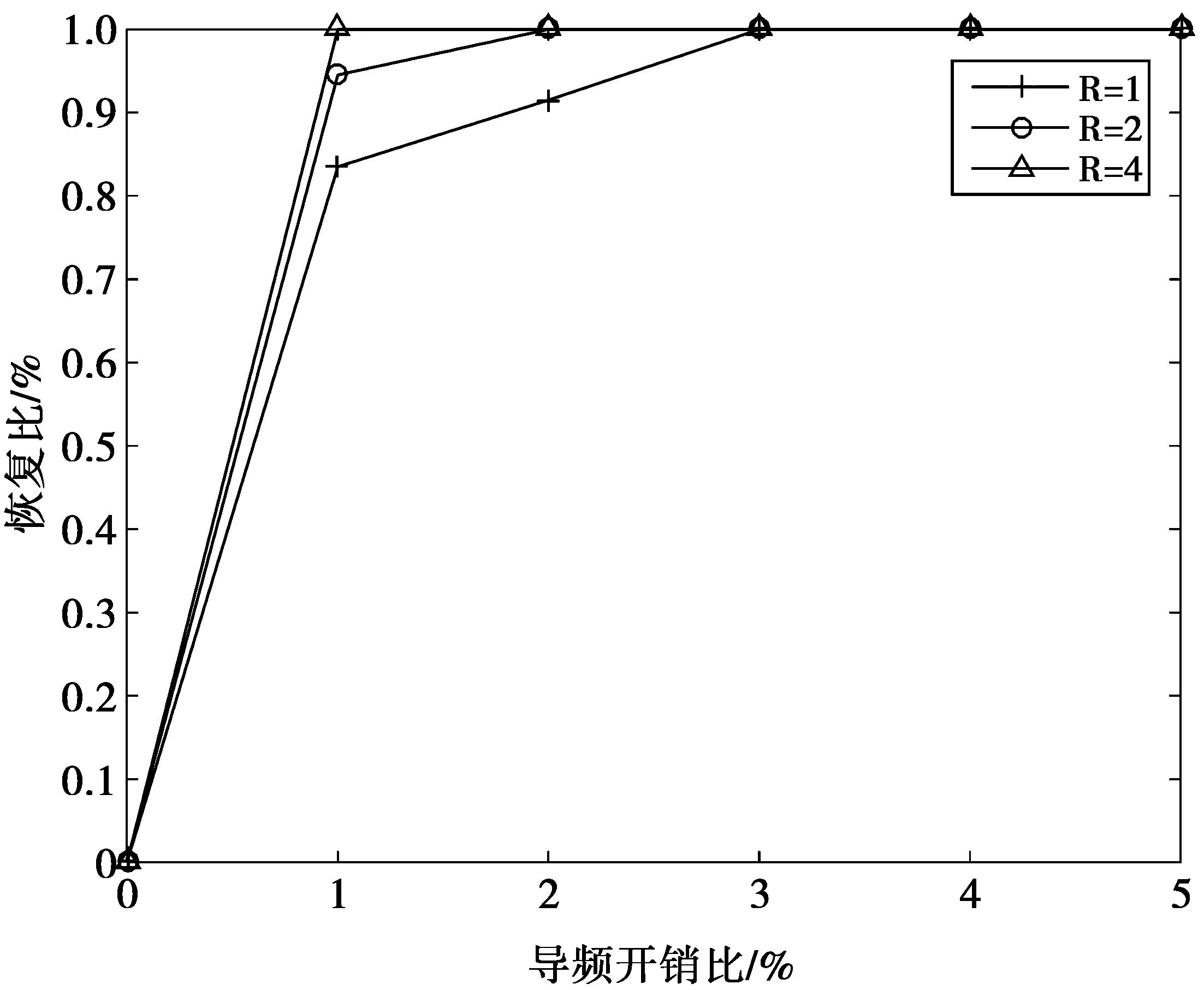
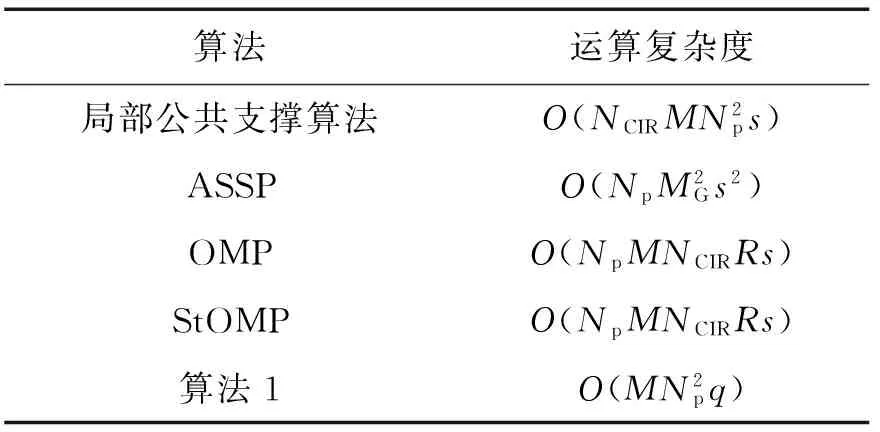
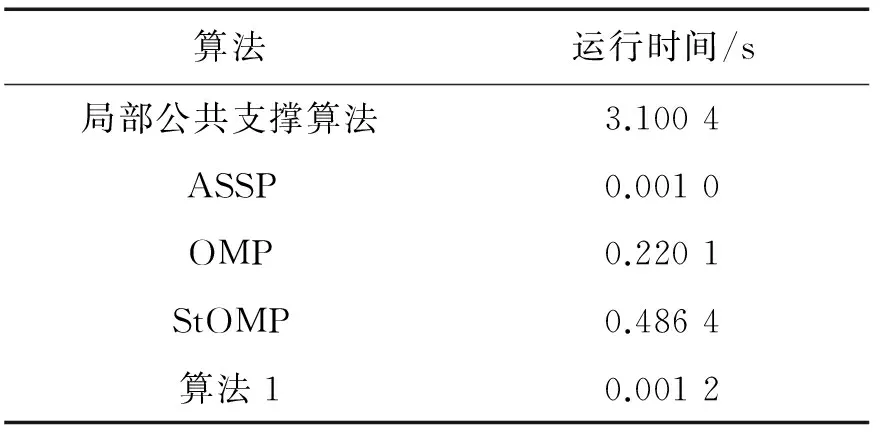
考虑一个单小区大规模MIMO-OFDM系统,该系统工作在FDD模式下,基站端配备M根天线,用户配备单根天线。假设每个包含导频的OFDM符号有NFFT个子载波,由NP个导频子载波以及NFFT-NP个数据子载波和保护间隔组成。在基站端,假设所有发射天线的导频占用完全相同的子载波,第m根发射天线的导频序列pm,维数为Np×1;μn={cn,1,…,cn,Np}表示随机导频子载波的下标集,可以从序列{1,2,…,NFFT}中随机获取。利用无线MIMO信道的稀疏性,可以大大减小用于信道估计的导频开销。NCIR表示时域CIR向量的长度,由于导频子载波的数量有限,存在NP< (3) (4) 对(4)式进一步简化,可得 (5) 对于一个无线大规模MIMO信道,L个连续的OFDM信号具有相同的导频模型,由(5)式可知每个OFDM信号导频为 (6) 则L个连续的OFDM信号接收的导频信号可表示为 (7) i=1,2,…,NCIR (8) (9) 由Jacks衰落模型可以得到CIR矩阵复杂增益的时间相关性,表示为 (10) (11) (11)式中:wi表示M×Np维与LMMSE估计相关的系数[12],表示为 (12) (13) (14) 利用(1)式和(2)式的空时相关性,本文提出算法1,在未预知稀疏度的条件下,通过处理L个相邻OFDM信号的接收导频以实现对大规模MIMO信道的估计,而且需要的导频开销较小,算法1具体步骤如下 步骤2若B(p)>A(q),则不再继续迭代,执行步骤11;否则进入步骤3。 步骤3相关性测试。 步骤4更新支撑集。Λ1(p)=Ω(p)∪Λ1(p-1)。 步骤5裁剪支撑集。 步骤7更新残留矩阵。 步骤8若B(p)>B(p+1),转至步骤9,否则转至步骤10。 步骤9令p=p+1,Ω(p)=Λ2(p-1),继续执行步骤2。 步骤10令q=q+1,A(q)=B(p),继续执行步骤2。 算法1与文献[9]中的局部公共支撑算法相比具有以下几方面差异:①局部公共支撑算法利用一个支撑向量来确定CIR向量的非零元素位置,该算法仅考虑一个发射—接收天线对的情况并从一个低维度测量向量中重构一个高维度稀疏向量。相反,在算法1中使用公共支撑集来确定CIR向量中的非零元素位置然后进行LMMSE估计,并且考虑许多发射—接收天线对的情况,利用大规模MIMO信道的空时相关性从低维度测量矩阵中恢复高维度稀疏矩阵,这种方式很大程度上减小了算法的运算时间,并能高效地恢复原始信号。②局部公共支撑算法需要预知信道稀疏度以实现对信道的估计,然而算法1可以自适应地获取稀疏度并完成矩阵估计。通过利用大规模MIMO信道的时间相关性和公共稀疏性,算法1设置自适应迭代停止标准B(p)>A(q),其中p,q分别为迭代下标和阶段值,停止标准随着残留矩阵的改变而改变,从而提高了信道估计的精确度。 为了验证提出的算法对于FDD大规模MIMO系统具有有效性,本文进行了如下仿真,系统参数为:OFDM子载波数N=4 096,基站端配备的天线数M=64,假设所有发射天线发送完全相同的随机导频,导频开销比为(Np/N)×100%,多普勒频移fd=70 Hz,每根天线中相邻OFDM信号的时间间隔Ts=0.5 ms,多径信道的最大延迟扩展为4.88 μs,相邻子载波间隔为7.5 kHz,CIR向量的长度NCIR=4.88 μs×7.5 kHz×4 096≈150,假设CIR向量中随机分布的非零元素个数为15个。 3.1 导频开销比对MSE性能的影响 图1比较了局部公共支撑算法、ASSP(adaptive structed subchannel pursuit)算法[11]、StOMP(stagewise orthogonal matching pursuit)算法[13]、OMP(orthogonal matching pursuit)算法[14]以及本文提出的算法1在不同导频开销时的归一化均方误差(mean squared error,MSE)性能。为进一步体现算法1的估计性能,给出了oracle[9]算法,该算法假设用户端已知信道稀疏度,属于算法1的特例。系统假设相邻OFDM信号数为R=1,信噪比SNR=20 dB。从图1中可以看出算法1的性能优于OMP算法、StOMP算法、局部公共支撑算法和ASSP算法,因为该算法利用MIMO信道的空时相关性,通过自适应地获取信道稀疏度,改善了信道估计性能。ASSP算法在矩阵估计过程中采用的是LS估计,LS估计没有LMMSE估计性能好。当导频开销比大于等于3%时,算法1与oracle算法具有相似的MSE性能。这表明算法1在低导频开销时能够可靠地获取信道稀疏度和稀疏支撑集。 图1 不同算法的导频开销比对MSE的影响Fig.1 MSE comparison of different algorithms versus pilot overhead ratio 3.2 信噪比对MSE性能的影响 图2比较了局部公共支撑算法、ASSP算法、OMP算法、StOMP算法、算法1以及oracle算法在不同信噪比时的MSE性能,其中假设相邻OFDM信号数为R=1,导频开销比为5%。从图2中可以看出随着SNR的增加,所有算法的MSE逐渐减小,且算法1的性能优于其它几种算法。 图2 不同算法的SNR对MSE的影响Fig.2 MSE comparison of different algorithms versus SNR 3.3 时间相关性对MSE性能的影响 图3比较了算法1在有无利用时间相关性时的MSE性能,仿真中R=1,2,4,SNR=20 dB。相邻OFDM信号数R=1和R=2,4分别表示没有和有利用无线MIMO信道的时间相关性,由图3可以看出,通过利用时间相关性,算法1表现出良好的信道估计性能。 图3 有无时间相关性时,MSE随导频开销比的变化情况Fig.3 MSE versus pilot overhead ratio with and without exploiting the temporal correlation 3.4 时间相关性对恢复比的影响 图4比较了算法1在有无利用时间相关性时的恢复比,仿真中R=1,2,4,SNR=20 dB。经过观察可知R=1和R=4时,算法1精确地恢复未知信号所需的导频开销比分别为3%和1%。因此利用时间相关性,算法1可以在精确恢复未知信号的同时减小导频开销。 图4 有无时间相关性时,恢复比随导频开销比的变化情况Fig.4 Recovery ratio versus pilot overhead ratio with and without exploiting the temporal correlation 3.5 运算复杂度和运行时间对比 表1 运算复杂度对比 注:MG为每个天线组中天线个数,s为信道稀疏度。 表2给出5种算法的平均运行时间运算时间。仿真中SNR=20 dB,R=1,导频开销比为3%。通过比较,可以观察出算法1比局部公共支撑算法、OMP算法和StOMP算法运行时间更短。由理论分析可知,算法1是选择与残留矩阵最匹配的几个列的下标,而OMP算法、StOMP算法和局部公共支撑算法每次只选择与残留矩阵最匹配的1个列的下标。与此同时算法1可以自适应地获取信道稀疏支撑集,OMP算法、StOMP算法和局部公共支撑算法则需要根据预设的稀疏度经过多次计算得到稀疏支撑集。ASSP算法采用LS估计比算法1运行的时间略短。局部公共支撑算法运算时间最长,因为该算法利用支撑向量b来计算LMMSE估计。 表2 运行时间对比 本文针对FDD大规模MIMO系统设计了一种基于空时相关性的信道估计算法。该算法不需要将稀疏度作为先验信息,而是经过反复计算自适应地获取信道稀疏支撑集并重构原始信号。仿真结果表明,提出的算法能够降低导频开销并保持良好的信道估计性能。 [1] 陈慧慧,凌荣桢,景小荣.基于空间相关性的大规模MIMO信道压缩反馈算法[J].重庆邮电大学学报:自然科学版,2015,27(5):589-594. CHEN Huihui, LING Rongzhen, JING Xiaorong. Compressed channel feedback for spatial correlated massive MIMO systems[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2015, 27(5): 589-594. [2] MARZETTA T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE Transactions on Wireless Communications,2010,9(11): 3590-3600. [3] LARSSON E G, EDFORS O, TUFVESSON F, et al. Massive MIMO for next generation wireless systems[J]. IEEE Communications Magazine,2014,52(2):186-195. [4] CHAN P W C, LO E S, WANG R R, et al. The evolution path of 4G networks: FDD or TDD[J]. IEEE Communications Magazine, 2006, 44(12): 42-50. [5] RAO X, LAU V K N. Distributed compressive CSIT estimation and feedback for FDD multi-user massive MIMO systems[J]. IEEE Transactions on Signal Processing, 2014, 62(12): 3261-3271. [6] 叶新荣.基于压缩感知重构算法的MIMO-OFDM稀疏信道估计方法研究[D].南京:南京邮电大学,2014. YE Xinrong. Research on sparse channel estimation in MIMO-OFDM systems based on compressed sensing reconstruction algorithms[D]. Nanjing :Nanjing University of Posts and Telecommunications,2014. [7] NGUYEN S L H, GHRAYEB A. Compressive sensing-based channel estimation for massive multiuser MIMO systems[C]//2013 IEEE Wireless Communications and Networking Conference(WCNC),USA: IEEE, 2013: 2890-2895. [8] DAI L, WANG Z, YANG Z. Spectrally efficient time-frequency training OFDM for mobile large-scale MIMO systems[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(2): 251-263. [9] CHOI J W, SHIM B, CHANG S H. Downlink pilot reduction for massive MIMO systems via compressed sensing[J]. IEEE Communications Letters, 2015, 19(11): 1889-1892. [10] SHEN W, DAI L, GAO Z, et al. Spatially correlated channel estimation based on block iterative support detection for massive MIMO systems[J]. Electronics Letters, 2015, 51(7): 587-588. [11] DAI L, GAO Z, WANG Z. Joint channel estimation and feedback with low overhead for FDD massive MIMO systems[C]//2015 IEEE/CIC International Conference on Communications in China(ICCC), China: IEEE, 2015: 1-6. [12] CHO Y S, KIM J, YANG W Y, et al. MIMO-OFDM wireless communications with MATLAB[M]. John Wiley & Sons: Chichester. England 2010. [13] DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094-1121. [14] 杨真真,杨震,孙林慧.信号压缩重构的正交匹配追踪类算法综述[J].信号处理,2013,29(4):486-496. YANG Zhenzhen, YANG Zhen, SUN Linhui. A survey on orthogonal matching pursuit type algorithms for signal compression and reconstruction[J]. Journal of Signal Processing, 2013, 29(4): 486-496. (编辑:张 诚) PilotreductionusingspatialandtemporalcorrelationinmassiveMIMOsystems JIN Feng, ZHANG Jinyan, YIN Lixin (Chongqing Key Lab of Mobile Communications Technology, Chongqing University of Post and Communications, Chongqing 400065, P. R. China) In the massive multiple input multiple output (MIMO) systems, the base station sends pilot signals for channel estimation at users. Since the number of pilots is proportional to the number of transmit antennas, pilot overhead required by conventional channel estimation can be prohibitively large, especially for frequency-division duplexing (FDD) massive MIMO. To solve this problem, we present a pilot overhead reduction algorithm based on compressive sensing (CS) techniques by utilizing the spatially common sparsity and temporal correlation in wireless MIMO channels, whereby the spatial and temporal correlation is exploited to improve the channel estimation accuracy. The proposed algorithm can adaptively acquire the accurate channel state information without the knowledge of the sparsity level of massive MIMO channel. Analysis and simulation results show that the proposed algorithm outperforms Locally Common Support Algorithm in pilot overhead reduction, and it is capable of achieving good channel estimation performance. massive MIMO; spatial and temporal correlation; channel estimation; compressive sensing(CS) The Changjiang Scholars and Innovative Research Team in University of China(IRT1299) TN92 A 1673-825X(2017)05-0642-07 金 凤(1993-),女,河北人,硕士研究生,主要研究方向为移动通信。E-mail:2530299308@qq.com。 张进彦(1992-),山东人,硕士研究生,主要研究方向为移动通信。E-mail:913577355@qq.com。 尹礼欣(1993-),安徽人,硕士研究生,主要研究方向为移动通信。E-mail:790740805@qq.com。 2016-11-28 2017-05-26 金 凤 2530299308@qq.com 长江学者和创新团队发展计划(IRT1299). 10.3979/j.issn.1673-825X.2017.05.010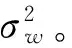
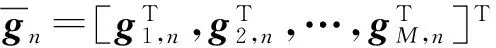
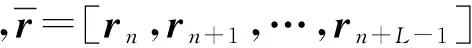

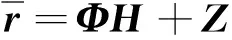
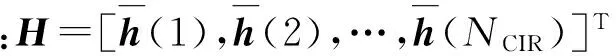
2 提出的信道估计算法
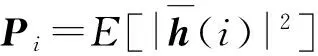
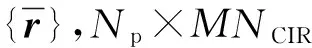
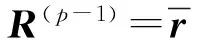

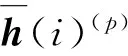
3 仿真实现及分析
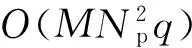
4 结 语



