合理展开封头曲面的研究

2017-11-01郑鹏飞赵菊娣林大钧

东华大学学报（自然科学版） 2017年4期

关键词：椭圆形封头曲面

郑鹏飞，王波，赵菊娣，林大钧，安琦

(1.华东理工大学机械与动力工程学院，上海 200237；2.义乌工商职业技术学院机电信息学院，浙江义乌 322000)

合理展开封头曲面的研究

郑鹏飞1， 2，王波2，赵菊娣1，林大钧1，安琦1

(1.华东理工大学机械与动力工程学院，上海 200237；2.义乌工商职业技术学院机电信息学院，浙江义乌 322000)

根据测地线的短程性与线上各点测地曲率为零的几何特性，采用在不可展的封头曲面上构建由测地线与法截线交织成线网的方法来获得椭圆形封头和球形封头展开图的边界，并建立对应的数学模型，结合计算机编程，为参数化展开封头曲面提供简便、稳定可靠的方法.以曲面理论面积为评判标准，该方法展开精度高于工程上常用的几种近似展开方法和CAD软件的展开精度.

测地线；封头；不可展曲面；数学模型；展开精度

在机械制造领域中经常会涉及曲面展开问题，特别是对不可展曲面的近似展开.不可展曲面的近似展开是航空航天、船舶制造和化工设备行业中的一项重要技术.国内外学者为此进行了广泛研究，提出了各种曲面展开方法与技术[1-5]，如有限元法、几何逼近法[6]、力学模型法[8-9]、能量方程法[11-12]、三维软件法[7]、三角网格法[10，13]等.金玲等[6]利用AutoCAD对刚结构管构件进行曲面展开，但这类管构件属于可展曲面，并未涉及不可展曲面的展开技术.黄鹏[7]利用CATIA软件进行二次开发，对不可展曲面进行分割提取并展开.韩林等[8]利用弹簧-质点模型，将曲面三角化，以三角点作为质点，三角边为弹簧，构建能量方程，计算质点的约束力，虽可进行曲面展开，但其计算过程较复杂，且计算量较大.现阶段针对化工设备中的封头曲面展开的相关研究较少.化工设备中椭圆形封头和球形封头的制造方法是将封头曲面分成若干等分，利用画法几何原理在平板上展开各部分，然后模压各块展开的平板使之成为封头曲面，再将模压成型的各部分封头曲面焊接成整体封头.制造过程中如何在平板上展开封头曲面，将直接影响成型封头的形状、精度及板材成本.

椭圆形封头的几何形状为半个回转椭球面，与球面一样，均属于不可展曲面.目前采用的几种封头曲面近似展开方法缺乏合理性.本文采用在不可展曲面上构建测地线和法截线线网的方法来展开椭圆形封头和球形封头，简称测法结合法，并选择展开面积和理论面积之比作为评价标准，以评价其合理性.

1 建立数学模型

图1 回转椭球面展开图解模型Fig.1 A flattening graphical model of ellipsoid

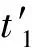
1.1测地线与法截线交点的确定

设o1点在oxyz坐标系中的坐标为o1(x0， 0，z0)，则有

(1)

又o1点满足

(2)

由(1)和(2)可得

(3)

图1中坐标系o1x1y1z1与坐标系oxyz的转换关系为

(4)

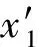
x1轴在oxyz坐标系中的斜率为

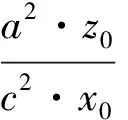
(5)

将式(1)代入式(5)中得

(6)

由此将式(3)和(6)代入式(4)中可得

(7)

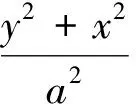
(8)

将式(7)代入式(8)中求解，可得当z1=0时o1x1y1z1平面与回转椭球面的交线为G+E+F=1.

其中：

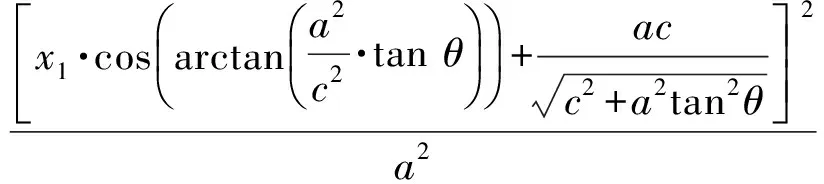
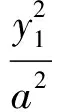
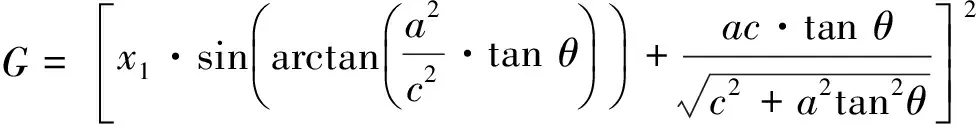
经整理得：

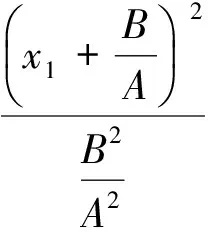
(9)

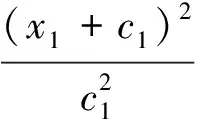
(10)

式(9)中A、B为

(11)

另外，铅垂面π1与回转椭球面的交线Ⅰ的方程为

(12)

正垂面π与回转椭球面的交线Ⅱ的方程为

(13)

将式(1)、(3)与式(13)结合可得

(14)

则交线Ⅰ与交线Ⅱ的交点为

(15)

由式(15)可解出交点的x，y，z坐标值为

(16)

其中J(θ)，H(θ)，K(θ)为

(17)

1.2椭圆离心角

根据x，y，z可分别求出图1中ψ与θ的函数关系以及θ与θ′的函数关系，下面分别述之

1.2.1ψ与θ的函数关系

由图1可知

(18)

由式(18)可得

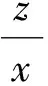
(19)

将式(16)中的x和z代入式(19)可得

(20)

1.2.2θ与θ′的函数关系

(21)

由此可得

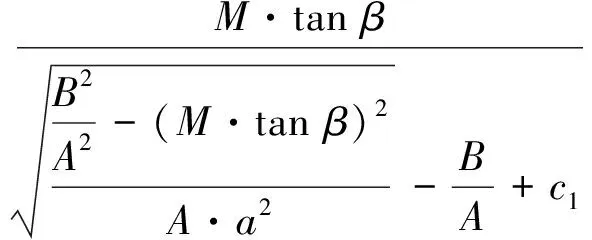
(22)

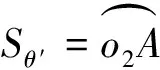
(23)

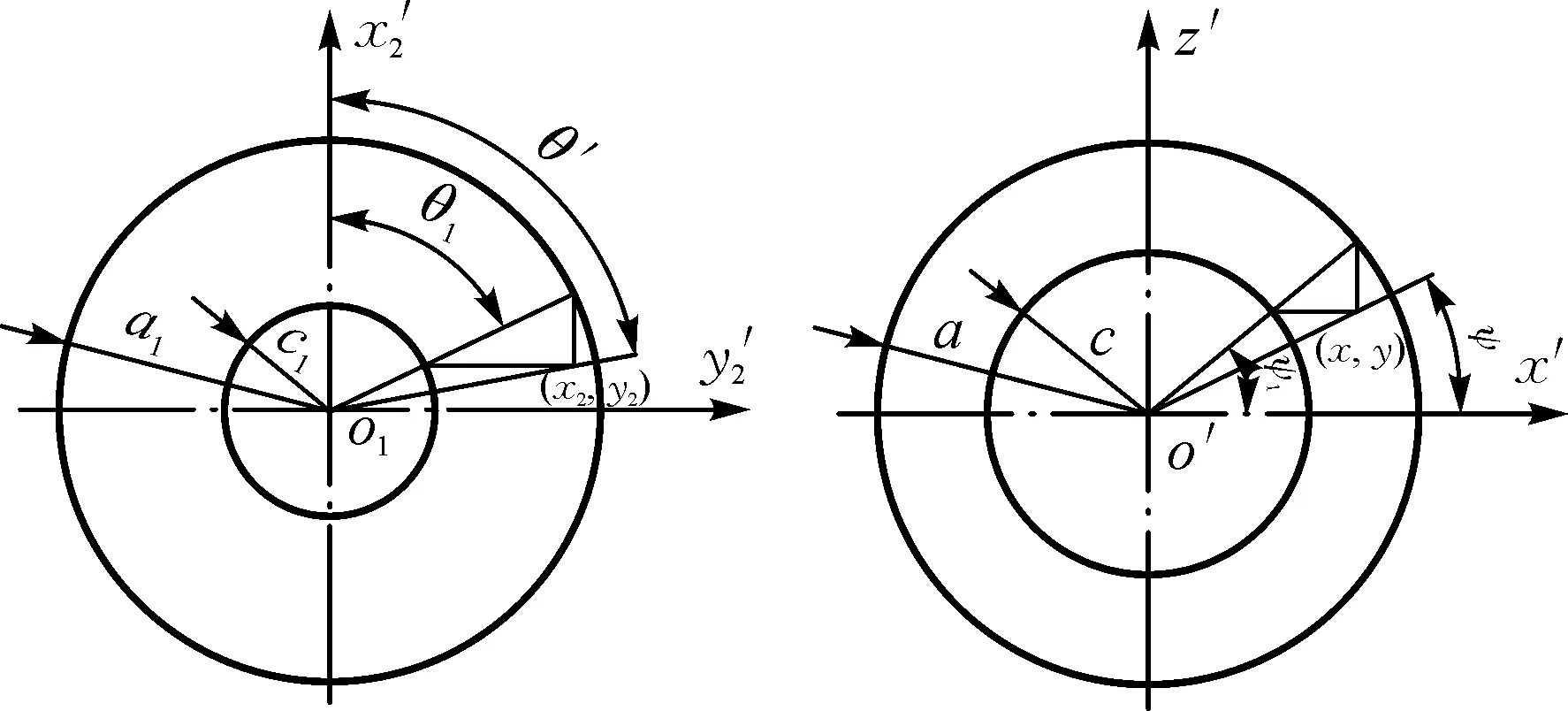
图2 圆心角与离心角的关系Fig.2 Relationship between the center angle and centrifugal angle

1.3展开图平面坐标系

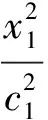
令x1=c1·sint，y1=a1·cost，则有

由此得Sθ ′弧上各点的曲率半径为

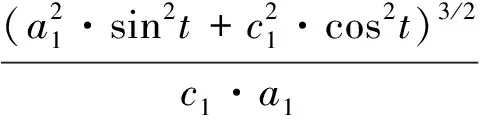
(24)

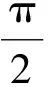
(25)

图3 展开图坐标系Fig.3 Coordinate system of flattening

式(25)即为椭圆形封头曲面展开的数学模型，由该式可求得某一块曲面展开边界上各点的S和L坐标值，最后将所求得的一系列点光滑连接即得到一条展开曲线.以此方法可得到椭圆形封头位于π1、π2两平面之间曲面的展开图.

2 算例验证

因椭圆形(回转椭球面)与球形(球面)均为不可展曲面，所以此类封头制造中采用了各种近似的展开方法，包括CAD软件.但理论上不可展的曲面不管用何种方法进行展开，客观上均有误差存在.以展开面积与理论面积之比作为评判标准，可用来鉴别各种展开方法的优劣.

2.1椭圆形、球形封头的理论面积

球形封头的理论面积计算过程较为简单，可由球表面积计算公式得到.椭圆形封头的理论面积A理论，则可根据回转椭球面方程：r={a·cosφ·cosα1，a·cosφsinα1，c·sinφ}，由式(26)计算得到.

(26)

2.2测法结合法展开椭圆形、球形封头的面积

为了验证测法结合法的有效性，现对椭圆形封头和球形封头分别进行测试.椭圆形封头：长半轴长为5 m，短半轴长为3 m，其理论表面积为117.368 m2；球形封头：球半径为R=5 m，其理论表面积(一半)为：157.080 m2.

根据上述椭圆形、球形封头的尺寸，针对不同的β角度值，自动计算并绘制其展开效果图，如图4所示.表1列出了两种封头曲面的理论面积与展开面积的比较结果，可见本法精度高达99%.

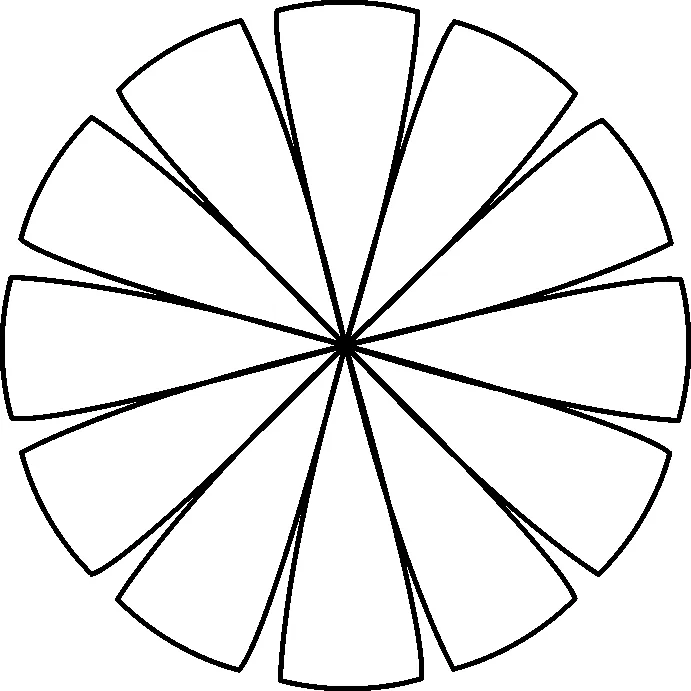
(a) 椭圆形

(b) 球形

表1 椭圆形和球形封头曲面展开面积误差对比表

2.3各种展开方法的展开面积比较

以球形封头为例，各种近似展开方法的展开面积误差结果如表2所示.将球面分成12份，当R=1 250 mm 时，球面理论面积：A理论=19.635 m2.由表2可知，用测地线法展开的面积误差最小(0.002 6%)，精度最高.

表2 不同展开法的面积误差对比表

3 结语

本文提出了一种通过在封头曲面上构建测地线与法截线线网而进行曲面展开的几何方法，并通过椭圆形封头和球形封头曲面展开算例验证了该方法的正确性和精确性.此法也可拓展为测地线法在封头曲面上建立全测地线网进行曲面的展开.因球面测地线比较简单，并且本文篇幅有限，故文中未对球面的测地线网构建过程进行详细描述，仅给出了结果以便与各种近似展开方法进行对比.

在封头曲面上构建线网这一几何模型是建立在曲面展开数学模型的基础上.根据数学模型进行计算机参数化的曲面展开，本文提出了形、数、计算机结合解决问题的有效路径.以封头曲面的理论面积与展开面积之比作为评价各种近似展开方法优劣的标准，为判断展开封头曲面的合理性提供了技术参考.在后续的研究工作中，可考虑更多的曲面展开评价指标，如拼缝长度等，提出更多合理的自由曲面上的测地线计算、复杂不可展曲面的测地线展开法等.

[1] GAN M C， TAN S T， CHAN K W. Flattening developable bi-parametric surfaces[J]. Computers & Structures， 1996， 58(4)：703-708.

[2] ZHANG Q L， LUO X Q. Finite element method for developing arbitrary surfaces to fattened forms[J]. Finite Elements in Analysis and Design， 2003(39)：977-984.

[3] 张文俊，刘婷，张贤杰，等.整体壁板数字化展开建模方法[J].航空制造技术，2016，508(13)：56-61.

[4] 潘炜，吴慧，李铁瑞，等.基于曲面展开的自由曲面网格划分[J].浙江大学学报(工学版)，2016，50(10)：1973-1979.

[5] 崔晓坤，陈明.快速可展窄带曲面设计[J].计算机应用研究，2012， 29(10)：3997-4000.

[6] 金玲，陈浩，张云飞.钢结构设计中复杂曲面的计算机展开[J].上海应用技术学院学报(自然科学版)，2010，10(2)：97-100.

[7] 黄鹏.样板设计中曲面展开问题及展开方法研究[J].航空制造技术，2014(S1)：155-157.

[8] 韩林，刘斌.基于弹簧-质点模型的三角网格曲面展开算法及其应用[J].华侨大学学报(自然科学版)，2011，32(6)：601-606.

[9] 梁堰波，徐伟辰，李吉刚，等.基于力学模型的曲面展开通用算法[J].计算机工程与设计，2012，33(9)：3539-3543.

[10] 詹雯，周来水，陈功.一种复杂曲面展开的通用算法[J].机械制造与自动化，2007，36(1)：83-87.

[11] WANG C C L， SMITH S S F， YUAN M M F. Surface flattening based on energy model[J].Computer-Aided Design， 2002，34(11)：823-833.

[12] 严国彪，刘斌.一种基于能量模型的曲面展开改进算法[J].华侨大学学报(自然科学版)，2011，32(2)：135-139.

[13] 陈功，周来水，安鲁陵，等.一种通用的复杂曲面展开方法研究[J].中国机械工程，2007，18(24)：2914-2920.

(责任编辑：杨静)

由表3可知：从检出率上看，本文算法的检出率相比模板匹配算法和分层检测算法分别高出了15．80%和23．97%，达到97．32%；从平均耗时上看，本文算法比前两种算法分别减少了24．30%和6．66%．不论从检出率还是检出速度上，本文算法均能满足印刷工业的要求．

StudyonReasonableFlatteningofHeadSurface

ZHENGPengfei1， 2，WANGBo2，ZHAOJudi1，LINDajun1，ANQi1

(1.School of Mechanical and Power Engineering，East China University of Science and Technology，Shanghai 200237， China；2.School of Mechanical Information， Yiwu Industrial & Commercial College， Yiwu 322000， China)

According to the two geometric characteristics of geodesics that the path between two points is the shortest and the geodesic curvature at every point equals zero， the boundary of the flattening ellipsoidal head or spherical head is computed by weaving a mesh with geodesics and normal sections on the undevelopable head surface. A simple， stable， reliable and parameterized undevelopable surface flattening method is proposed， and the corresponding mathematical model is established by its computer programming. The theoretical area of surface is used as the criteria for evaluation. It can be seen from the experimental examples that the flattening accuracy of the method is higher than other usual methods and CAD software aided method.

geodesic； head； undevelopable surface； mathematical model； flattening accuracy