薄壁圆柱壳的动态优化设计方法

王 娇， 于 涛， 张曰浩， 韩清凯

(1.烟台大学a.机电汽车工程学院；b.山东省高校先进制造与控制技术重点实验室；c.工程实训中心， 山东 烟台 264005；2.大连理工大学 机械工程学院， 辽宁 大连116023)

薄壁圆柱壳的动态优化设计方法

王 娇1a， 1b， 于 涛1a， 1b， 张曰浩1c， 韩清凯2

(1.烟台大学a.机电汽车工程学院；b.山东省高校先进制造与控制技术重点实验室；c.工程实训中心， 山东 烟台 264005；2.大连理工大学 机械工程学院， 辽宁 大连116023)

为了降低薄壁圆柱壳模态共振条件下的振动幅值与振动应力水平以及提高抗高周疲劳能力，研究薄壁圆柱壳的不同厚度和材料参数对其振动应力的影响，并采用有限元法计算薄壁圆柱壳关键位置节点处的动应力和振动响应.研究结果表明，薄壁圆柱壳存在最优的厚度值，其厚度增加到一定程度可以有效地降低薄壁圆柱壳的动应力.然而，改变薄壁圆柱壳的材料参数对其振动应力的影响较小.

薄壁圆柱壳； 动态优化设计； 振动应力； 振动位移

由于先进航空发动机要求尽可能高的推重比/功重比和工作效率，因而其结构形式往往精巧而复杂.然而，所采用的结构效率更高的薄壁构件如盘鼓组合结构等处于高温、高压、高转速的工作状态时，特别是存在复杂边界条件和载荷条件的情况下易于产生高阶共振现象.因此，在工程实际中，由于振动过大、封严齿碰摩等原因，薄壁圆柱壳容易发生裂纹损伤[1].

机械结构的动态优化设计，是指在结构动力修改和预测分析过程中，首先判断结构的薄弱环节，然后根据条件和可能进行的试探修改，使用优化方法进行设计过程[2-3].目前，旋转薄壁构件的动态优化设计过程存在很大局限.薄壁圆柱壳的结构动态优化设计的目标为：在保证高周疲劳强度(即特定共振频率下的振动应力幅值满足高周疲劳强度安全要求)的基础上，确定最小的结构尺寸.由于薄壁圆柱壳的振动特性、边界条件和载荷条件比较复杂[4]，在进行结构优化时，特别需要对薄壁结构的振动特性与响应规律进行深入研究，在此基础上才能实现高质量、低成本的薄壁结构动态优化设计，减小试验件检验，满足薄壁构件的工程应用需求.动态优化设计技术是薄壁构件振动分析、试验与验证的动态设计理论与方法体系的重要组成部分.

1 结构优化的内容和方法

以动应力为目标，薄壁圆柱壳结构优化设计是对薄壁圆柱壳有限元模型进行谐响应分析，以获得某阶固有频率和振型下的动应力. 考虑到发动机的实际结构情况，一般不容许对薄壁圆柱壳宽度和直径做设计上的改动，因此，本研究只以薄壁圆柱壳壁厚参数、材料参数作为设计变量，对薄壁圆柱壳进行结构优化分析.

(1) 优化目标. 以提高抗高周疲劳能力为目标，对薄壁圆柱壳进行优化分析.针对薄壁圆柱壳在气动激励条件下产生特定模态(m=1，m为轴向半波数；n=3，n为轴向半波数模态)的共振状态[5]，进行壳体厚度、壳体材料的改变，对比分析振动响应与振动应力的变化规律，以降低关键部位振动应力的水平.

(2) 设计参数的约束条件. 当薄壁圆柱壳的结构、材料参数变化时，其固有频率和响应将会改变.为了使薄壁圆柱壳的动态响应满足振动设计，达到设计目标，在薄壁圆柱壳的材料参数和厚度变化范围一定(2.2～3.2 mm)等约束条件下，进行合理的结构优化.

(3) 优化设计方法. 根据薄壁圆柱壳工作的实际情况给出其动应力的求解方法，采用数值方法进行优化计算[6-10].研究薄壁圆柱壳结构参数(厚度、材料参数)对其关键位置(第一个篦齿后一周节点)动应力的影响来进行薄壁圆柱壳的动态设计.

2 基于薄壁圆柱壳厚度的动态优化设计方法

考察篦齿结构对薄壁圆柱壳的振动响应和振动位移的影响，建立带有篦齿结构的薄壁圆柱壳. 对两种不同厚度(2.2 和3.0 mm)下的薄壁圆柱壳进行谐响应分析，研究圆柱壳的壁厚对其振动响应和振动位移的影响.薄壁圆柱壳的有限元模型如图1所示，模型采用Solid 186单元划分网格，单元数为11 952个，节点数为41 760个，薄壁圆柱壳与盘采用24个螺栓连接，因此，采用约束24个螺栓处节点的全部自由度，更加接近真实的边界条件.模型的弹性模量为2.06×1011Pa，密度为7 850 kg/m3，泊松比为0.3.应用ANSYS有限元软件，采用模态叠加法对薄壁圆柱壳进行谐响应分析，扫频范围为900～1 600 Hz，步长为1 400，阻尼比为0. 0003 (DMPRAT命令).为了模拟叶片和轮盘传递给薄壁圆柱壳的激振力，对其施加一个等效的力矩(一对力偶)，经过多种激励载荷方法的施加，只有上述方法能够获得m=1和n=3下振型的固有频率.将一对力偶作用在薄壁圆柱壳与盘连接处，激振力为100 N，激励力的位置如图1所示.

图1 薄壁圆柱壳施加一对力偶的有限元模型Fig.1 Finite element model of thin-walled cylindrical shell with force applied

2.1关键部位篦齿处的振动响应和振动应力分布

带有篦齿结构的薄壁圆柱壳厚度为2.2 和3.0 mm 时的振动幅值和振动应力分别如图2和3所示.

由图2可知，薄壁圆柱壳厚度增加后，其相应的振动幅值最大值由2.53×10-6m降低至2.21×10-7m，下降了约90%，说明圆柱壳厚度对其振动幅值的影响较大.由图3可知，随着薄壁圆柱壳厚度的增加，其最大振动应力由2.13 MPa下降至0.17 MPa，降低了92%，降低幅度比较大.

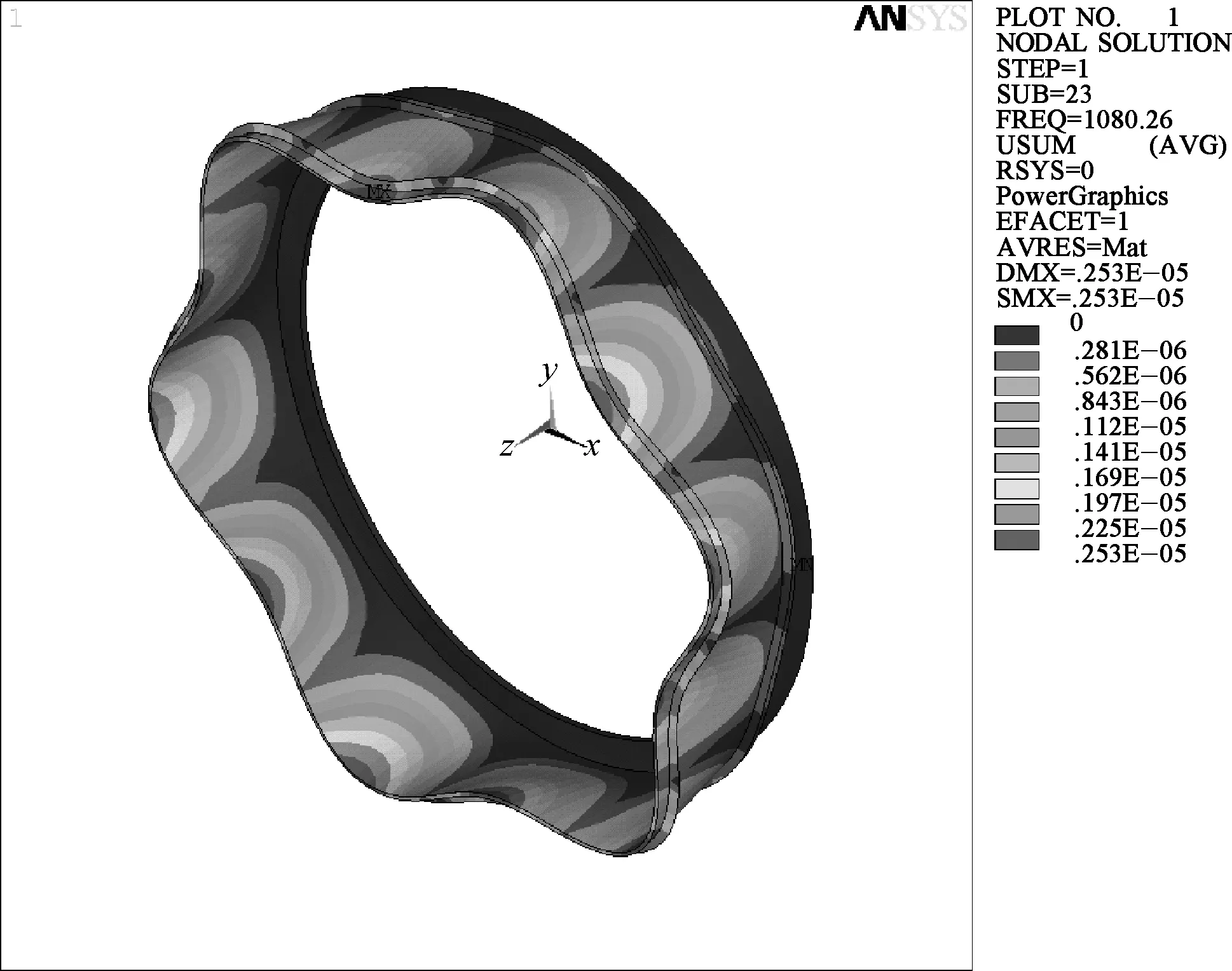
(a) 厚度为2.2 mm (b) 厚度为3.0 mm

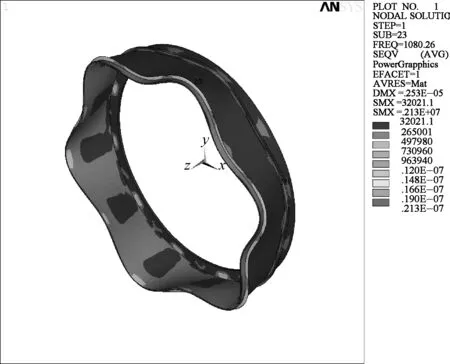
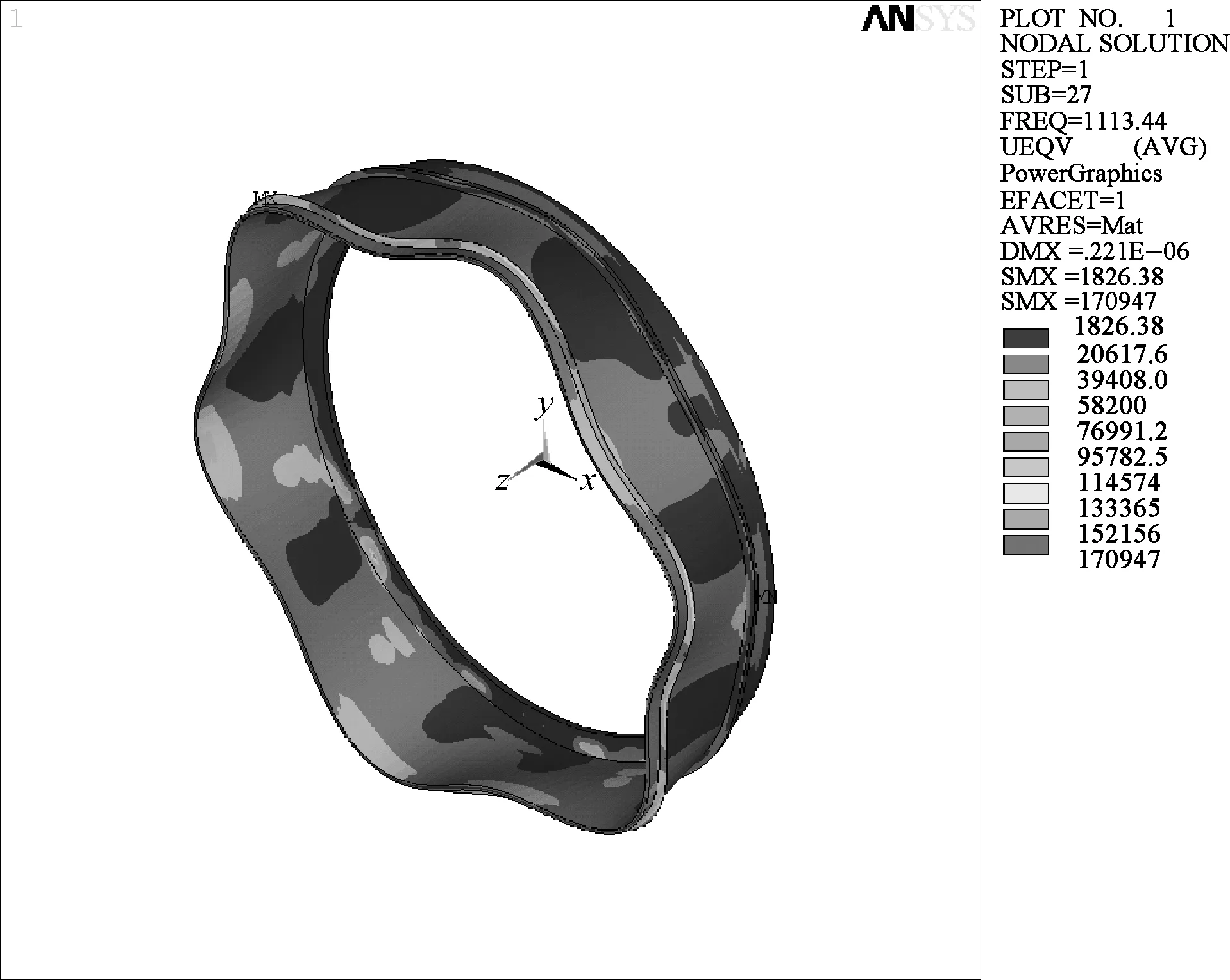
(a) 厚度为2.2 mm (b) 厚度为3.0 mm

2.2厚度变化对壳结构振动的影响变化规律分析

改变薄壁圆柱壳的厚度对其进行优化，厚度分别设置为2.2、 2.4、 2.6、 2.8、 3.0和3.2 mm.取第一个篦齿后壳体上的一个圆周的节点，对比分析响应和应力，寻找振动响应和振动应力随厚度变化的规律.第一个篦齿后(距离约束端为76.5 mm的位置)一周(144个节点)的节点应力如图4所示.

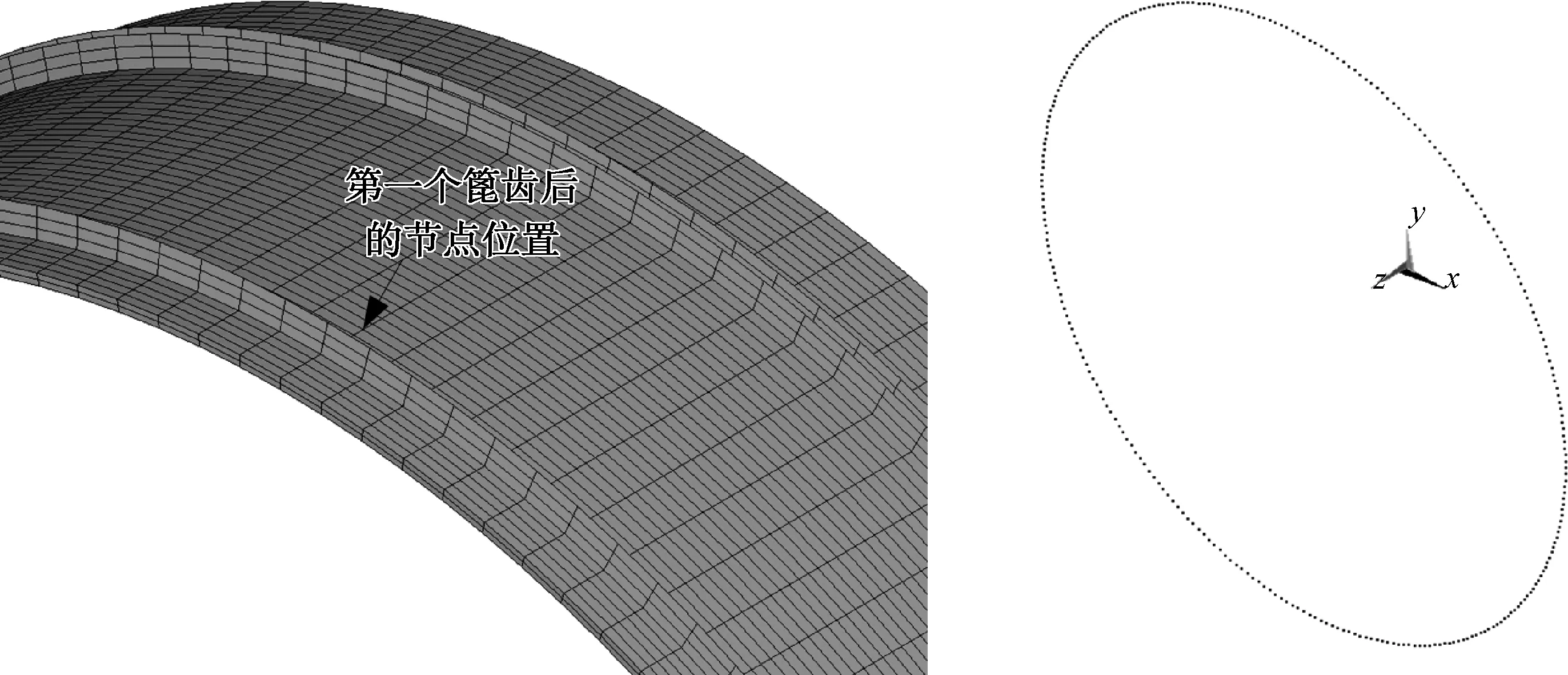
图4 薄壁圆柱壳第一个篦齿后的一周节点Fig.4 The nodes after the first labyrinth of thin-walled cylindrical shell

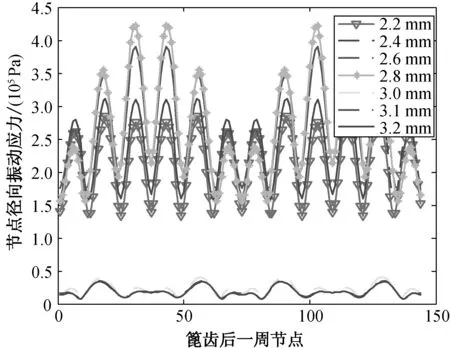
不同厚度薄壁圆柱壳对应的篦齿后一周节点(提取m=1，n=3振型)的径向振动应力如图5所示，厚度的整体影响规律如图6(a)所示.

由图6(a)可知，随着薄壁圆柱壳的厚度增加，第一篦齿后的相应的节点应力逐渐增大，但是当厚度增加到3.0 mm后，薄壁圆柱壳的节点径向振动应力突然降低，且降低的幅度较大，说明薄壁圆柱壳的厚度存在最优值，改变薄壁圆柱壳的厚度可以降低薄壁圆柱壳的振动应力.

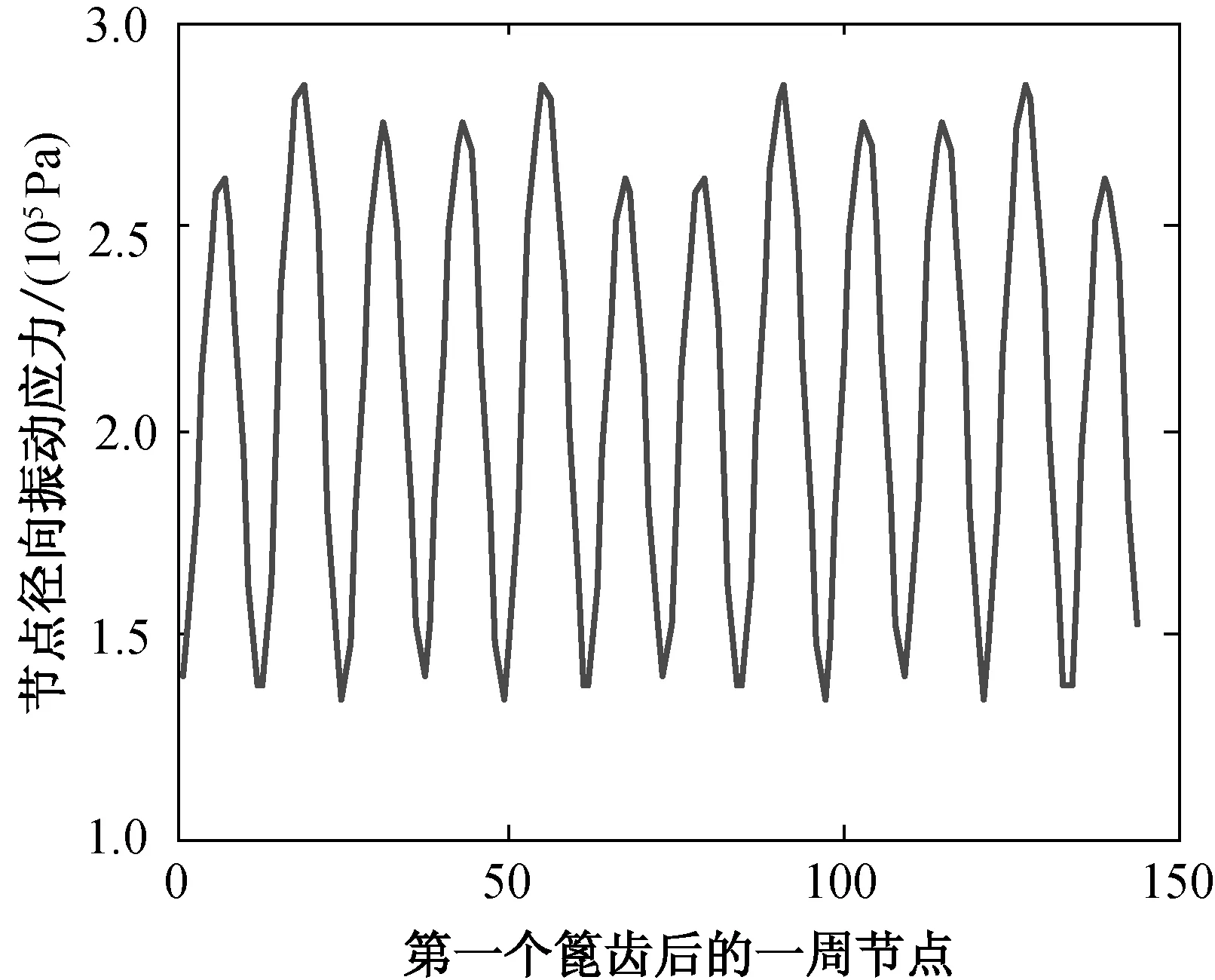
(a) 厚度为2.2 mm

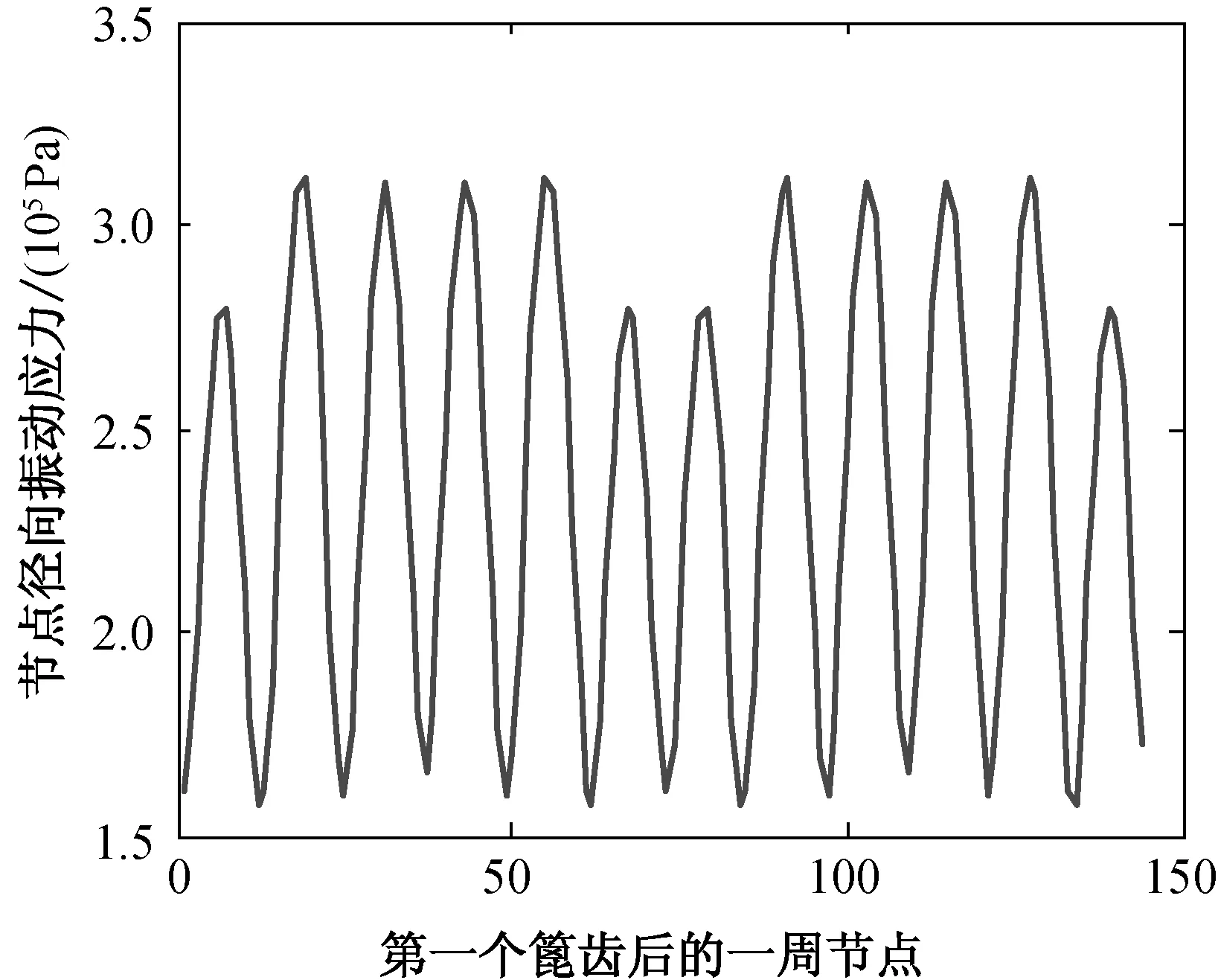
(b) 厚度为2.4 mm

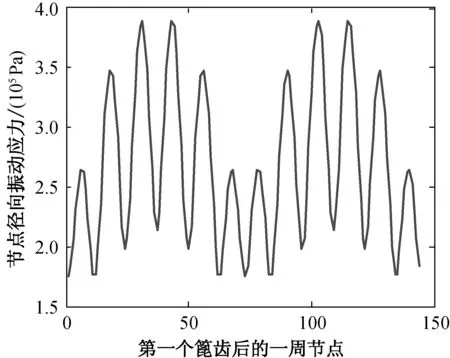
(c) 厚度为2.6 mm

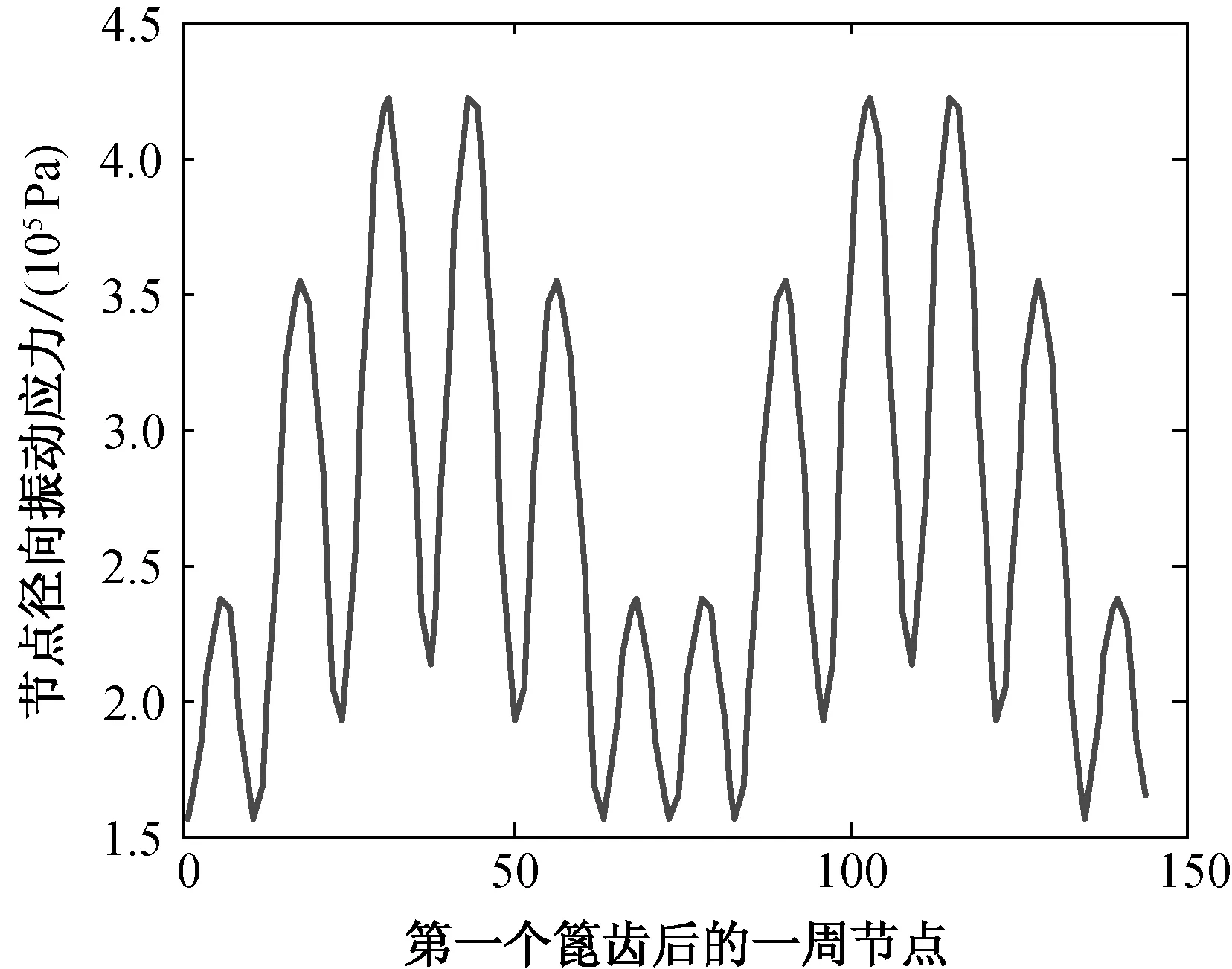
(d) 厚度为2.8 mm

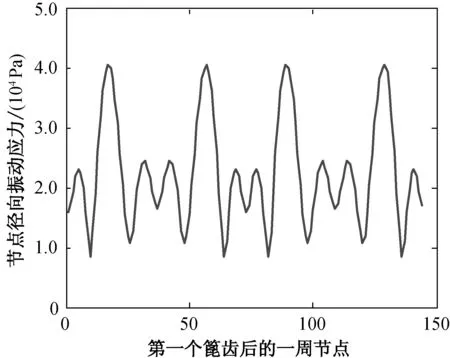
(e) 厚度为3.0 mm

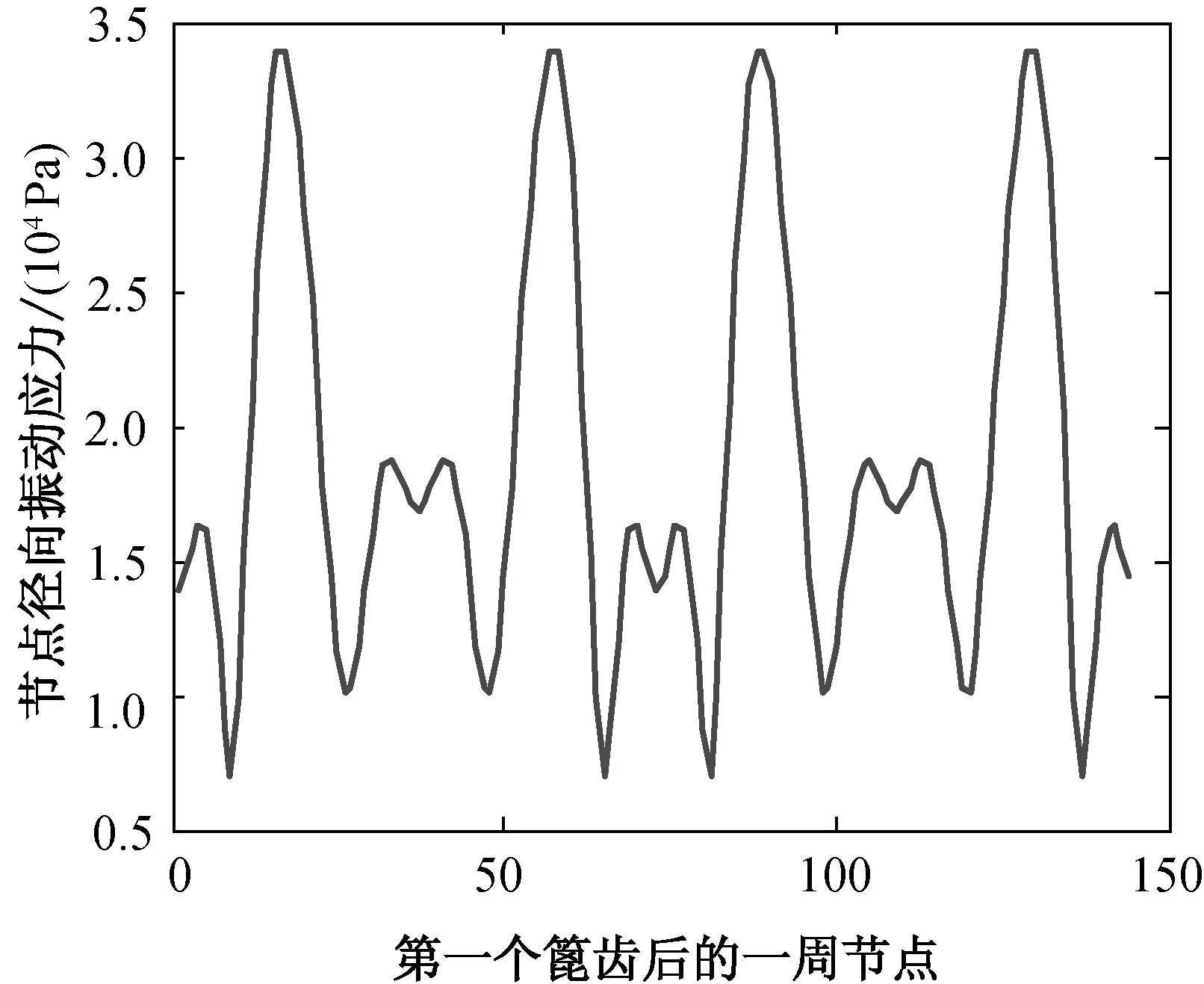
(f) 厚度为3.2 mm

图5不同厚度薄壁圆柱壳对应的篦齿后一周节点的径向振动应力
Fig.5Radialvibrationstressofthenodesafterthefirstlabyrinthofthin-walledcylindricalshellwithlabyrinthunderdifferentthickness

为了获得降低薄壁圆柱壳振动应力的最优厚度值，在薄壁圆柱壳壁厚为2.8～2.9 mm之间取了5个壁厚，分别为2.83、 2.84、 2.85、 2.86和2.88 mm，并对其进行谐响应分析，获得不同厚度下的第一个篦齿后的振动应力，结果如图6(b)所示.由图6(b)可知，当厚度增加到2.84 mm后，薄壁圆柱壳的节点应力突然降低，且降低的幅度较大，说明薄壁圆柱壳的厚度为2.84 mm时为最优厚度值.

(a)

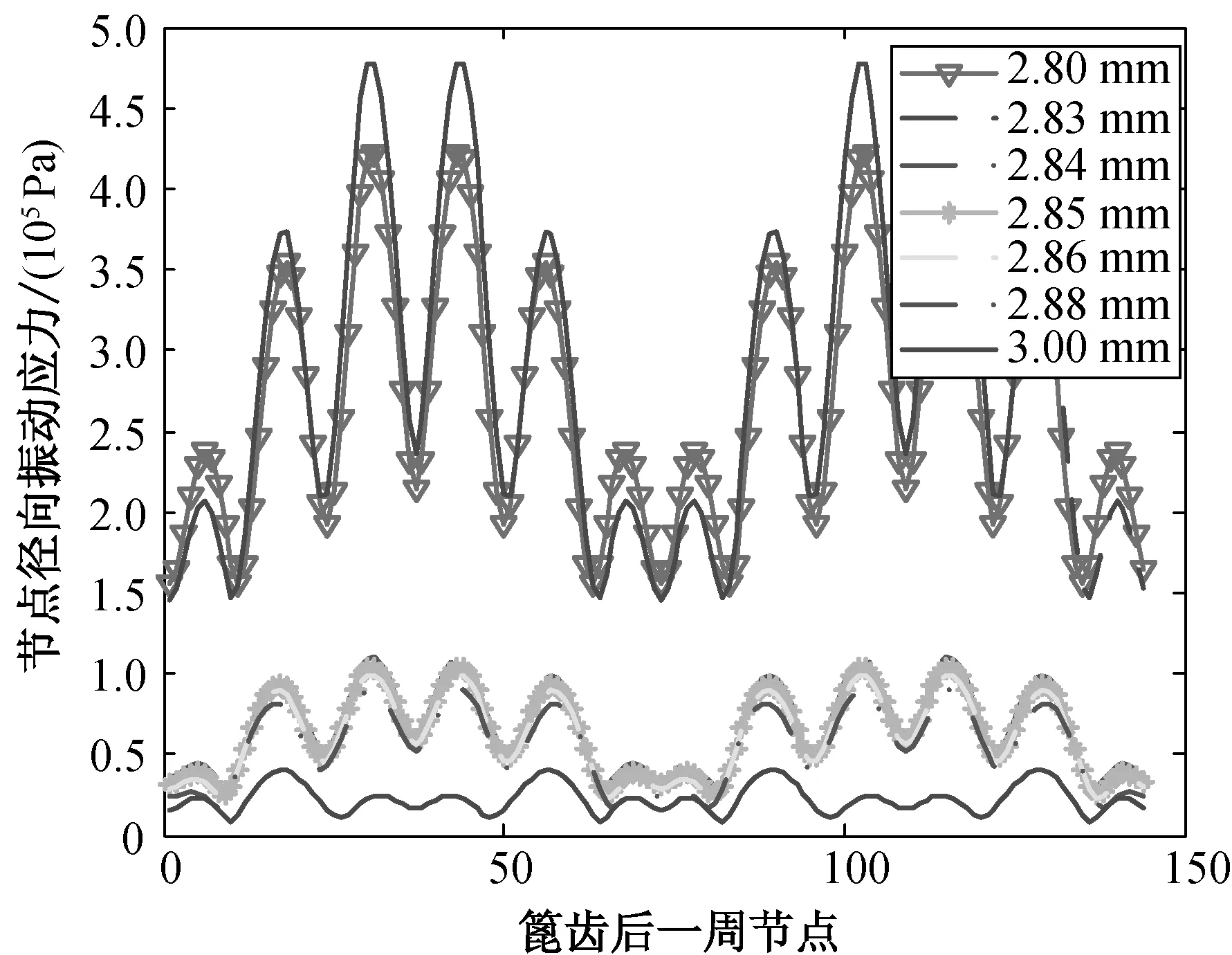
(b)

3 基于薄壁圆柱壳材料参数的动态优化设计方法

为了研究材料参数(如弹性模量)对薄壁圆柱壳结构优化设计的影响，采用了与真实结构件相同的钛合金材料，其材料的弹性模量为1.09×1011Pa，密度为4 480 kg/m3，泊松比为0.3.由于钛的弹性模量取值在105～120 GPa之间，因此分别取弹性模量为105、109、115 和120 GPa，在薄壁圆柱壳厚度分别为2.2和3.0 mm条件下进行谐响应分析，获得弹性模量对薄壁圆柱壳关键位置节点应力的影响，结果如图7所示.由图7可知，对于同一种材料，弹性模量对薄壁圆柱壳的振动应力影响较小，在薄壁圆柱壳达到最优厚度时(3.0 mm)，振动应力下降明显.

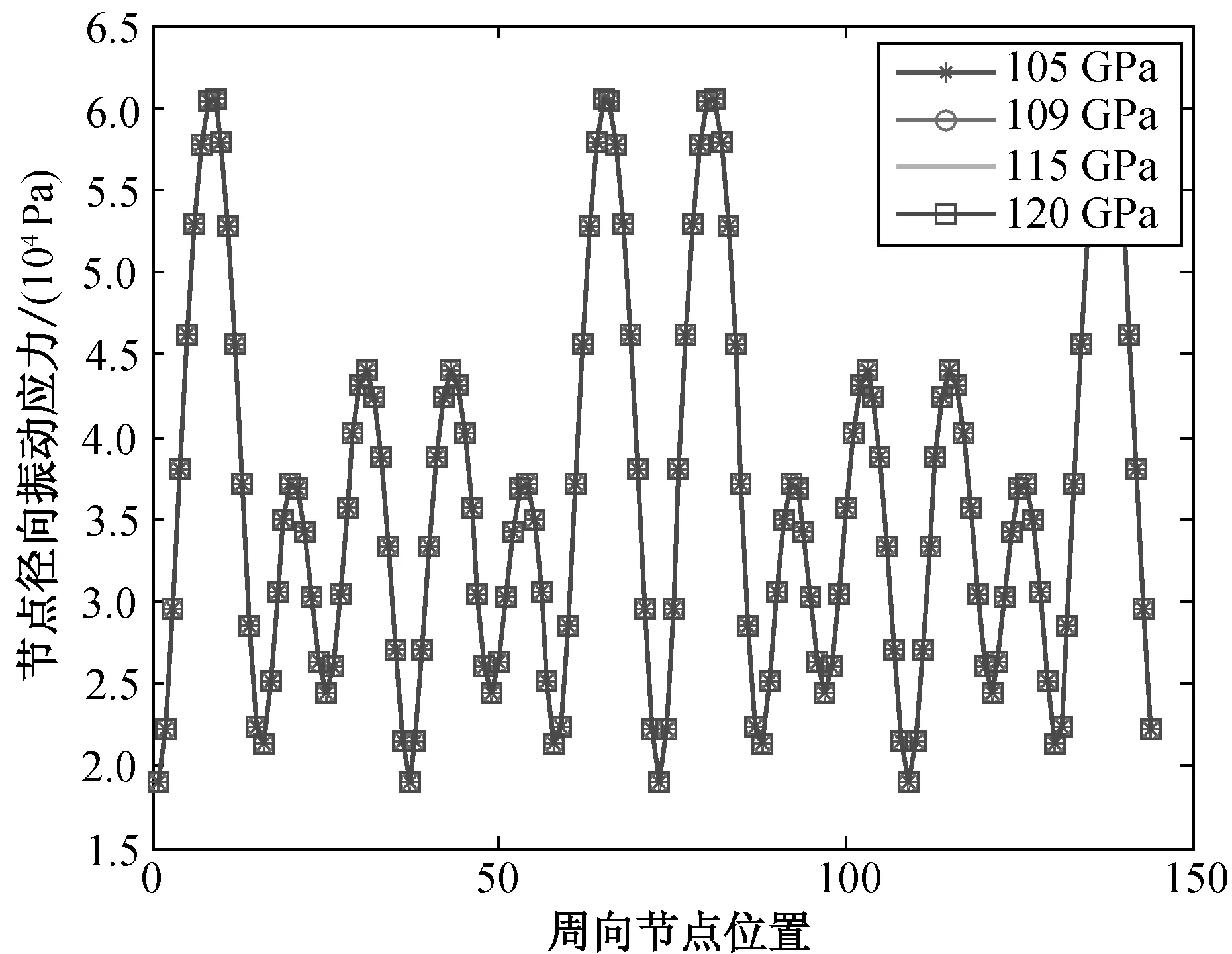
(a) 厚度为2.2 mm

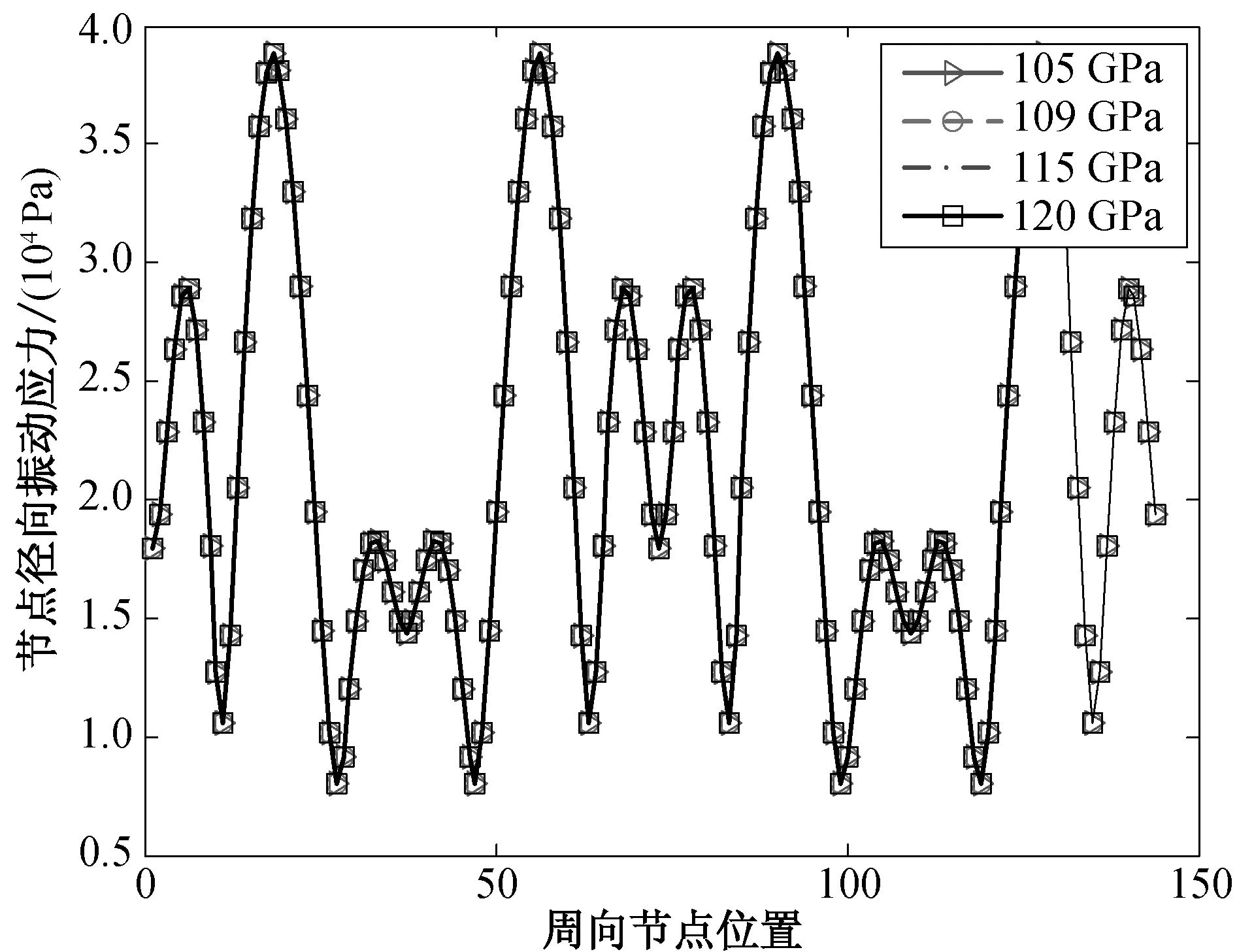
(b) 厚度为3.0 mm

4 结 语

针对薄壁圆柱壳动态优化设计目标，通过改变薄壁圆柱壳的厚度和材料，降低了其在模态共振条件下的振动响应与振动应力水平、提高了抗高周疲劳能力，并且可以在一定范围内改变其振动特性.利用有限元动响应与动应力计算的方法得到的结果如下：

(1) 随着薄壁圆柱壳的厚度增加，相应的节点应力随着厚度的增加而增大，但是薄壁圆柱壳的厚度存在最优值，当厚度增加到3.0 mm后，薄壁圆柱壳的节点应力突然降低，且降低的幅度较大，说明薄壁圆柱壳的厚度达到一定值时，可以使薄壁圆柱壳的振动应力降至最低.

(2) 对于同一种材料，不同弹性模量对薄壁圆柱壳的振动应力影响较小.

[1] 晏砺堂，朱梓根.结构系统动力特性分析[M].北京：北京航空航天大学出版社，1989：371-377.

[2] 赵宁，吴立言，刘更，等.叶片-轮盘结构动态特性形状优化设计[J].燃气涡轮试验与研究，1999，12(3)：45-47.

[3] 张志强，郭京波.机械动态优化设计综述[J].石家庄铁道学院学报，2005，18(1)：74-76.

[4] 刘彦琦，秦朝烨，褚福磊.不同边界条件下旋转薄壁圆柱壳的振动特性[J].清华大学学报(自然科学版)，2012，52(1)：5-9.

[5] 孙述鹏.转动薄壁圆柱壳的动力学特性研究[D].哈尔滨：哈尔滨工业大学航天学院，2013.

[6] 毛佳，江振宇，陈广南.轴压薄壁加筋圆柱壳结构优化设计研究[J].工程力学，2011，28(8)：183-192.

[7] 徐士代，汪凤泉，路淼.基于特征值灵敏度修改的叶轮结构改进设计[J].流体机械，2004，32(8)：18-20.

[8] 吴元动，漆文凯.某发动机模拟机匣的模态分析与模型验证[J].机械科学与技术，2010，29(11)：1487-1492.

[9] GUO D， ZHENG Z， CHU F. Vibration analysis of spinning cylindrical shells by finite element method[J]. International Journal of Solids and Structures， 2002，39(3)：725-739.

[10] LIEW K M， NG T Y， ZHAO X， et al. Harmonic reproducing kernel particle method for free vibration analysis of rotating cylindrical shells[J]. Computer Methods in Applied Mechanics and Engineering， 2002，191(37)：4141-4157.

(责任编辑：杨静)

DynamicOptimizationDesignMethodofThin-WalledCylindricalShell

WANGJiao1a， 1b，YUTao1a， 1b，ZHANGYuehao1c，HANQingkai2

(a. School of Electromechanical and Automotive Engineering；b. Key Laboratory of Advanced Manufacturing and Control Technology in Universities of Shandong；c. Engineering Training Center， 1.Yantai University， Yantai 264005， China；2.School of Mechanical Engineering， Dalian University of Technology， Dalian 116023， China)

The influence of different thickness and material parameters on the dynamic stress of thin-walled cylindrical shell is studied so that to reduce the vibration amplitude and dynamic stress of thin-walled cylindrical shell under the condition of modal resonance， and improve the ability of anti-high cycle fatigue. The dynamic stress and vibration amplitude of the key position of thin-walled cylindrical shell are calculated by the finite element method. The results show that the thickness of thin cylindrical shell has the optimal value， and the dynamic stress can be reduced effectively by increasing the thickness of thin-walled cylindrical shell to a certain extent. The material parameters of the thin-walled cylindrical shells have little effect on the vibration stress.

thin-walled cylindrical shell；dynamic optimization design； vibration stress； vibration amplitude

V 232.6

A

1671-0444 (2017)04-0490-06

2016-12-30

国家自然科学基金资助项目(11502227)；山东省自然科学基金资助项目(ZR2014EEP006)；山东省科技发展计划资助项目(2013YD02045)

王 娇(1985—)，女，吉林辽源人，讲师，博士，研究方向为非线性振动、阻尼涂层减振等.E-mail：zoe_wangjiao@163.com