叶菜根系图像的变分水平集分割算法

冯太锐, 苗玉彬, 朱云开, 赵 爽

(1. 上海交通大学 机械与动力工程学院, 上海 200240; 2. 上海交通大学 医学院附属新华医院, 上海 200092)

叶菜根系图像的变分水平集分割算法

冯太锐1, 苗玉彬1, 朱云开2, 赵 爽1

(1. 上海交通大学 机械与动力工程学院, 上海 200240; 2. 上海交通大学 医学院附属新华医院, 上海 200092)

植物根系图像分割是根系构型特征提取和分析的前提. 针对传统图像分割方法在处理叶菜根系弱边缘图像中存在分割精度和稳定性较差的问题, 提出了一种基于改进C-V(Chan-Vese)模型的变分水平集分割算法. 该算法不仅保留了C-V模型对于处理弱边缘图像的适用性, 并针对叶菜根系图像局部灰度不均的特点引入了图像梯度信息, 改进了原C-V模型. 通过对小白菜根系样本图像的分割处理试验，证明了变分水平集分割算法的有效性. 研究结果表明， 相比传统的阈值处理、边缘检测及区域生长等算法, 本文算法能更加精细地解决叶菜根系图像弱边缘和局部灰度不均的问题, 并在分割精度和算法稳定性上具有明显的优势. 变分水平集算法应用于叶菜根系构型观测系统中, 可以有效地提高观测精度.

叶菜根系; 图像分割; 变分水平集方法; C-V模型

在植物生理学等学科研究中, 根系构型参数的准确测定是一个极为重要的课题. 由于根系生长介质不透明且形态复杂多变, 难以对其进行直接观测. 实际研究中通常采用的挖掘法、剖面法等传统方法，不仅耗时耗力, 而且容易损毁根系, 影响试验结果. 然而, 机器视觉技术可以在不破坏植物根系原有特征的基础上, 对其构型参数进行更加准确且快速的测定, 因此在相关学科研究中得到了广泛的应用. 在利用机器视觉技术对植物根系进行观测的过程中, 根系图像的分割是对根系构型参数进行提取和分析的前提与基础.叶菜根系构型复杂, 其图像存在弱边缘和局部灰度不均的缺陷, 因此一直是根系图像分割中的难点.

国外对植物根系观测技术的研究已经较为深入. 一些成熟的研究成果已经转化为了商业产品并投入市场, 如CID Bio-Science公司推出的CI-600 Root Scanner for Root Monitoring系统、Regent Instruments公司推出的Win RHIZO根系测量系统以及Bartz Technology Corporation公司推出的 BTC I-CAP图像采集和批量处理系统等等. 国内的研究起步较迟, 目前还处于理论研究阶段, 不过近年来在根系图像分割领域的研究发展快速. 文献[1] 提出了一种结合遗传算法和误差反向传播算法的神经网络算法, 通过构造三层前馈网络并以图像边缘特征向量为输入信号对人工神经网络进行训练， 仿真实验证明了该方法对于植物根系图像边缘检测问题有着更好的抗噪性能和准确度. 文献[2] 提出了一种基于多尺度小波变换和自适应阈值原理的图像边缘检测算法, 相比传统分割算法有着更好的抗噪性, 且分割出的轮廓更加接近真实轮廓. 文献[3] 研究了现有典型图像分割技术的特点，并提出了一种基于高斯滤波和Hessian矩阵的根系图像分割方法, 设计实现了以Matlab为环境的根系分割及定量分析系统. 目前, 根系分割基本都是以图像像素点及其邻域为基础构造算法, 然而对于灰度不均匀的叶菜根系弱边缘图像往往会出现误分割的现象.

本文利用变分水平集的原理, 构造了一种基于C-V(Chan-Vese)模型的叶菜根系图像分割算法. 在利用C-V模型的全局特性处理叶菜根系图像弱边缘和噪声问题的基础上, 针对图像局部灰度不均的特点在能量泛函中引入了图像梯度能量信息, 最终获得了分割效果和稳定性更好的改进C-V模型分割算法, 能够进一步提高叶菜根系构型测定的精度.

1 材料与方法

1.1算法概述

变分水平集方法是近几十年来飞速发展的一种图像处理方法, 其算法稳定、精度高且易于处理图像的拓扑结构变化, 其可广泛应用于图像分割、图像增强、目标跟踪、三维图像重建等领域中, 尤其在医学图像领域内有着独特的优势和极为广泛的应用[4-10].

变分水平集方法的实质是建立与图像信息相关的能量泛函, 并通过建立偏微分方程求解能量泛函最小值. 水平集模型的建立主要利用图像边缘和区域两类信息得以实现[11-15], 即边缘型分割模型和区域性分割模型. 传统的C-V模型是一种区域型分割模型, 该模型基于图像全局信息建立能量泛函从而对目标进行分割, 在处理弱边缘图像的分割中有着较为理想的效果. 本文以C-V模型为基础, 设计了一种针对叶菜根系弱边缘图像分割问题的改进C-V模型算法. 算法的具体实现过程如下: 首先, 建立传统的变分水平集C-V模型; 然后, 通过引入图像梯度信息建立改进C-V模型; 最后, 对获得的改进C-V模型水平集演化方程进行数值实现.

1.2基于图像全局信息的C-V模型

Chan等[14]提出的添加了惩罚项后的C-V模型能量泛函如式(1)所示.

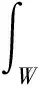
(1)

式中:u0为待处理图像的灰度函数;c1和c2为演化曲线C内部和外部的图像像素灰度平均值;λ1和λ2为取值为正值的权重参数, 一般取λ1=λ2=1;φ为水平集函数；H(φ)为Heaviside函数；W为待处理图像的全图像域. 当取得该能量泛函的最小值时, 演化曲线内外的灰度将趋于均匀, 于是不同灰度的目标和背景区域就被分割开来. 式(1)的后两项分别为长度约束项和面积约束项, 分别通过约束轮廓曲线长度和轮廓线内区域面积来影响演化.

利用变分原理和梯度下降流可得演化偏微分方程如式(2)所示.

(2)

为了提高计算效率, 式(2)中已用正则化的Dirac函数δε(φ)代替φ.c1和c2可根据定义由式(3)和(4)计算.

(3)

(4)

式(2)～(4)为C-V模型的水平集函数演化偏微分方程.

另外, 为避免水平集函数的周期性重复初始化, 本文将Li模型[15]中的符号距离保持项引入C-V模型. 引入该惩罚项后的演化偏微分方程如式(5)所示.

(5)

添加了符号距离保持项的C-V模型将根据全局灰度信息驱动轮廓曲线进行演化, 并且增强了演化过程的稳定性, 因此有着抗噪性能良好和对演化曲线初始位置不敏感的优点. 但是, 也仍然存在明显的弊端: 一方面, 其利用全局信息的特点使其计算量增大, 导致演化速度不够理想; 另一方面, 在叶菜根系图像分割处理过程中, 图像样本往往会存在一定程度的灰度不均匀的现象, 添加了符号距离保持项的C-V模型仅仅采用均值区分目标和背景, 可能出现分割效果不好或者误分割的问题. 针对上述问题, 本文在C-V模型的能量泛函中添加了图像梯度能量项, 从而构造出引入图像梯度信息的改进C-V 模型.

1.3引入图像梯度信息的改进C-V模型

在不考虑噪声的理想情况下,当演化达到稳定时, 演化曲线应当停留在目标边缘处. 强边缘图像中的边缘点往往是图像灰度梯度最大的点, 这一点对于边缘相对较弱的叶菜根系图像分割仍然具有参考意义. 考虑在传统的C-V模型中添加一个含梯度向量通量的惩罚项, 当演化曲线停留在边缘点时该惩罚项取到较小值, 由此可驱使演化曲线向着图像边缘附近运动. 构造的梯度能量惩罚项如式(6)所示.

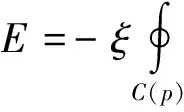
(6)

式中:C(p)为演化曲线;u0为待处理图像的灰度梯度;N为演化曲线的单位法向量. 由变分原理可得式(6)的梯度下降流如式(7)所示.

(7)

添加梯度能量惩罚项后, 根据变分法和梯度下降流可得改进C-V模型的水平集演化方程如式(8)所示, 该方程为本文算法的核心方程.

(8)

1.4水平集演化方程的数值实现

水平集函数初始化后, 在改进C-V模型水平集演化方程的驱动下, 零水平集上的曲线将逐步演化最终达到目标真实轮廓处. 该方程在数值实现中的关键在于对拉普拉斯算子()中的偏导数部分的数值进行近似处理, 对此可以采用有限差分方法实现. 有限差分方法分为前向差分、后向差分、中心差分等格式. 由于中心差分具有二阶精度, 高于前向差分和后向差分的一阶精度, 且实现复杂程度相差无几, 本算法采用中心差分格式.

将水平集演化方程表示为如下形式, 并采用中心差分格式近似代替式中有偏导数的项, 由此得到数值迭代计算如式(9)所示.

(9)

式中: Δt为时间步长;u0为待分割图像;φn+1为第n次迭代演化后的水平集函数. 其中, 参数μ,ν,γ,ξ需通过对叶菜根系样本进行大量试验对比来选定合适的值. 长度约束项参数μ和面积约束项参数ν取较小值时更易分割出细小的根系分支, 但也容易受到噪声的影响而误分割; 反之, 则曲线演化更加平滑且抗噪性更好, 但容易忽略一些较细小的根系目标. 符号距离保持项可以使水平集函数自动靠近符号距离函数从而避免重复初始化, 但其参数γ取值过小则无法达到效果, 取值过大则会影响曲线演化的效率, 甚至造成演化方向错误. 梯度能量项参数ξ直接影响了曲线演化对根系图像边缘的敏感性, 但取值过大则容易受到噪声的干扰而影响分割效果. 经过样本试验对比, 最终选定模型参数为：μ=65,ν=1.5,γ=0.001,ξ=10.0. 在叶菜根系样本的品种及生长期相同的情况下, 该参数组合的分割效果最为理想.

2 试验及分析

2.1水平集分割模型的演化过程

利用基于C-V 模型的变分水平集方法对小白菜根系样本图像进行处理, 所得的演化进程记录如图1所示. 由图1可知, 该模型对于弱边缘问题有较好的处理效果, 并没有因为边缘较弱而产生分割效果差或明显的误分割.

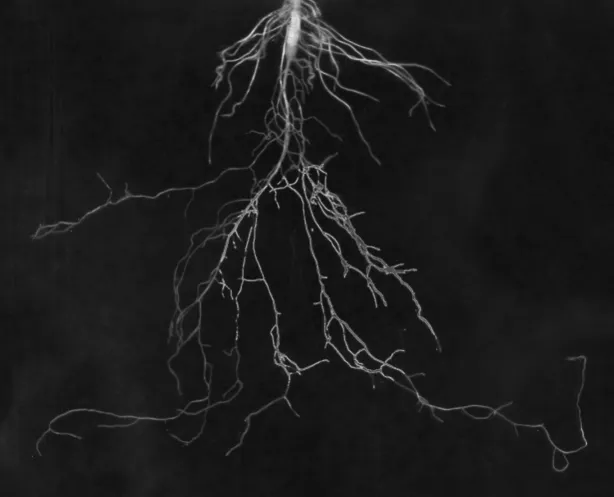
(a) 迭代50次

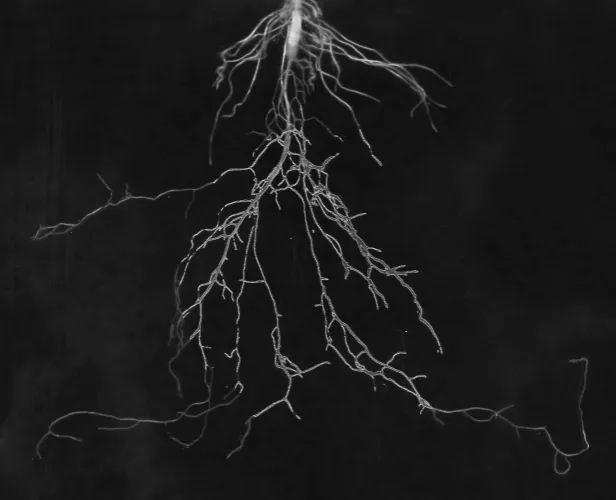
(b) 迭代100次

(c) 迭代200次

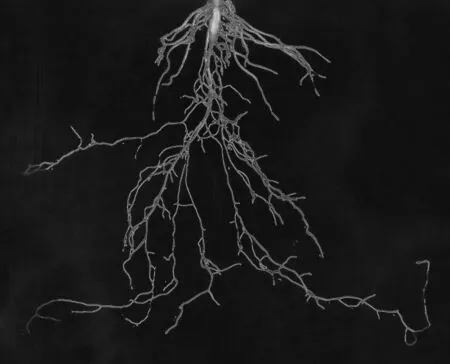
(d) 迭代500次

利用本文提出的基于改进C-V模型的变分水平集方法对小白菜根系样本图像进行处理, 并与原C-V模型的结果进行对比, 结果如图2所示. 由图2可知, 在同样迭代250次的情况下, 改进C-V模型相对于原C-V模型分割出的根系轮廓范围更广.

观察图2可以发现, 在根系目标的局部灰度不均处, 改进C-V模型对边缘的敏感度大大提升, 为算法引入梯度信息所产生的效果. 在迭代250次的条件下算法改进获得的小白菜根系细节样本图像如图3所示, 原C-V模型在灰度不均的位置演化受到了阻碍, 而改进C-V 模型则将该处轮廓较好地分割了出来, 即加速了演化进程.

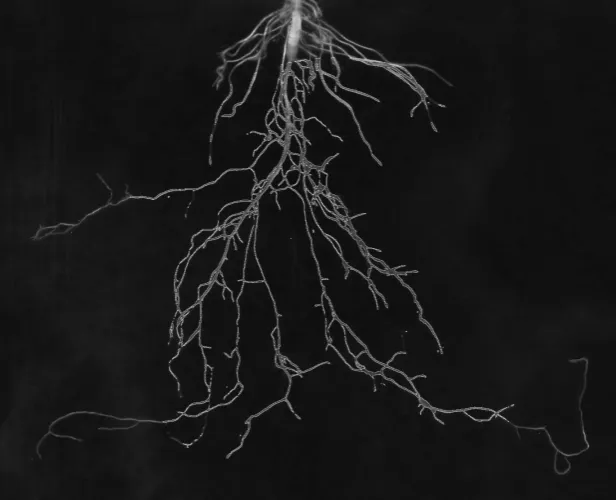
(a) C-V模型

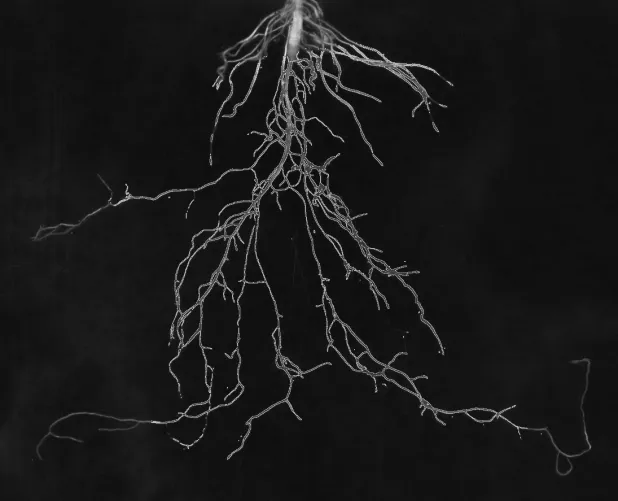
(b) 改进C-V模型

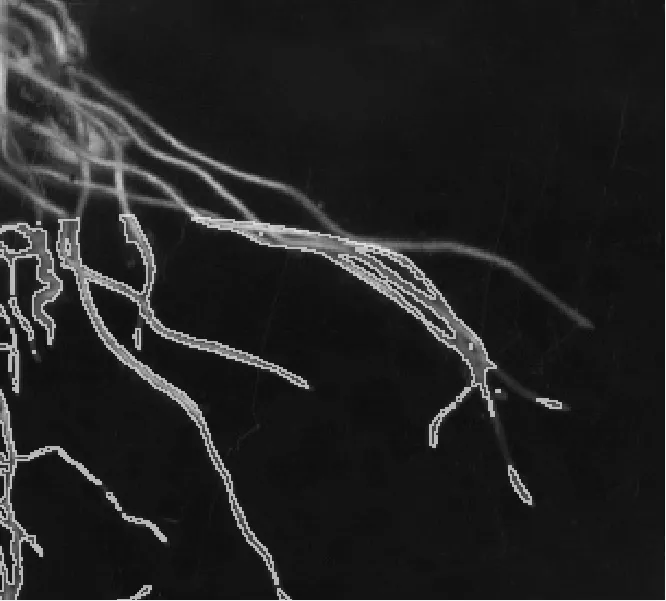
(a) C-V模型

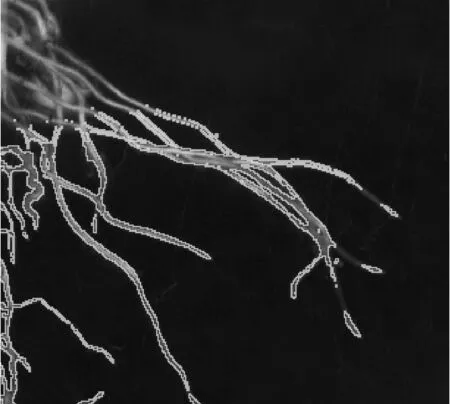
(b) 改进C-V模型

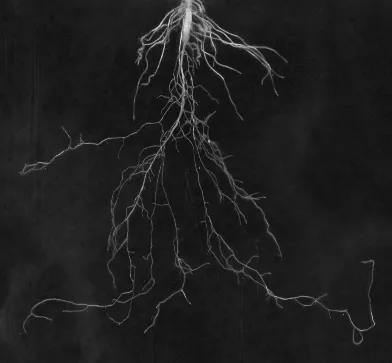
(a) 1号样本

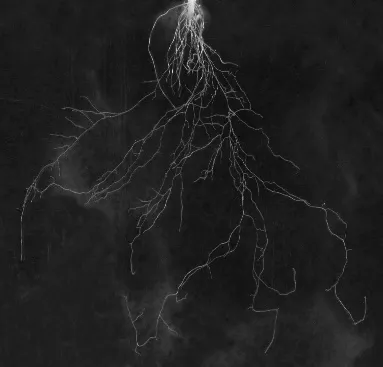
(b) 2号样本

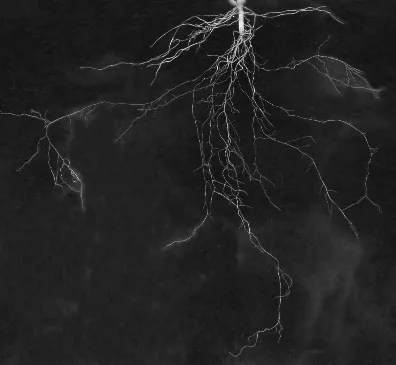
(c) 3号样本

为了比较改进C-V模型在演化效率上的优势, 本文在对小白菜根系1～3号样本图像(如图4所示)的处理过程中记录其演化完成所需的计算时间, 结果如表1所示. 测试环境为Intel(R) Core(TM) i5-4460 CPU @ 3.20 GHz, 由表1可以发现，改进C-V模型的算法在计算速度上具有一定程度的提升.

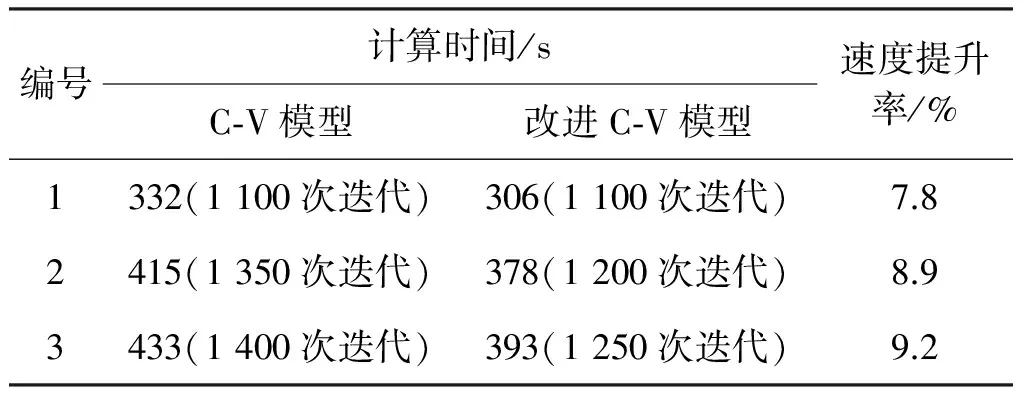
表1 小白菜根系图像分割完成所需计算时间Table 1 Computing time to segment pakchoi cabbage images

2.2小白菜根系图像分割结果

以小白菜根系样本原图像(见图4)为处理对象, 分析3种典型的传统图像分割算法的处理结果,并与本文的叶菜根系图像分割算法进行对比.

采用基于阈值分割的Otsu最佳全局阈值法[16]对小白菜根系样本图像进行分割处理所得的结果如图(5)所示. 由图5(a)和5(c)可知, Otsu最佳全局阈值法取得了较为良好的分割处理结果, 但在图5(b)中发现， Otsu阈值法所分割的图像出现了过分割的现象. 由此可见, Otsu最佳全局阈值法用于叶菜根系的分割存在稳定性欠佳, 尤其对于背景灰度不均匀的图象很容易出现误分割的问题.

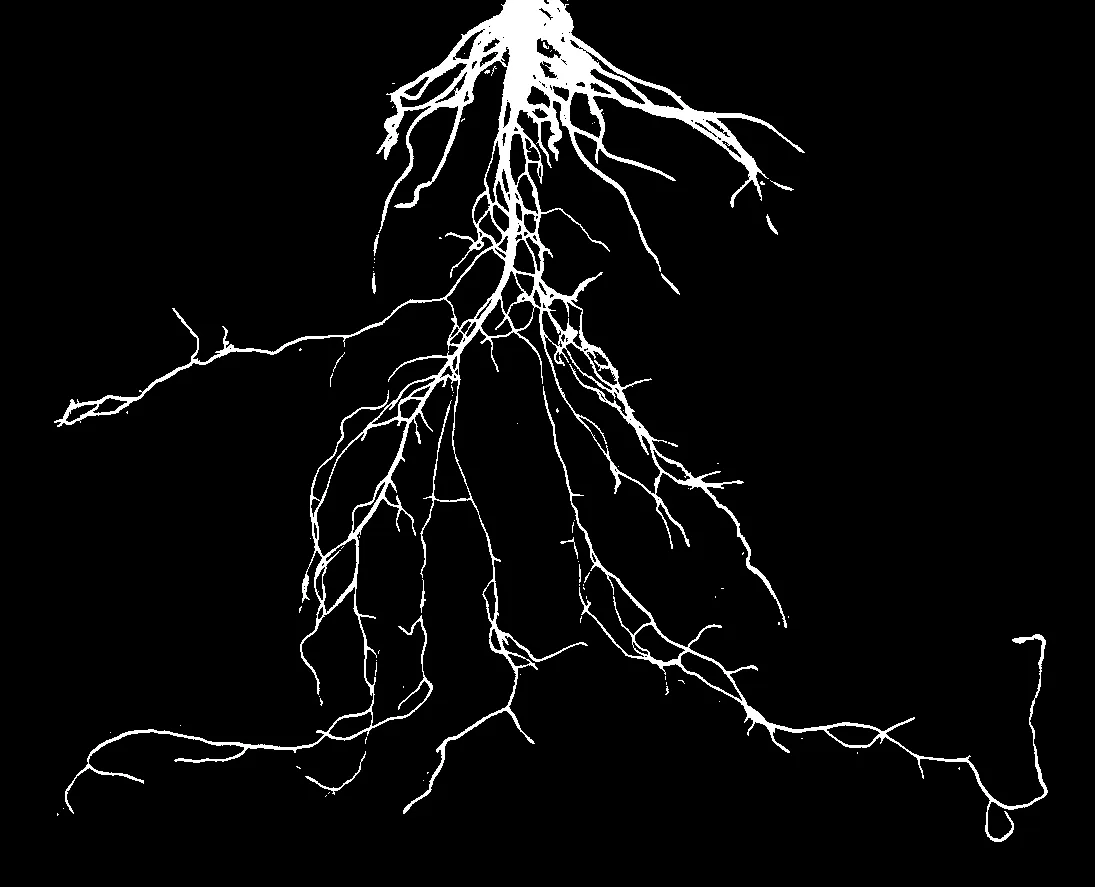
(a) 1号样本

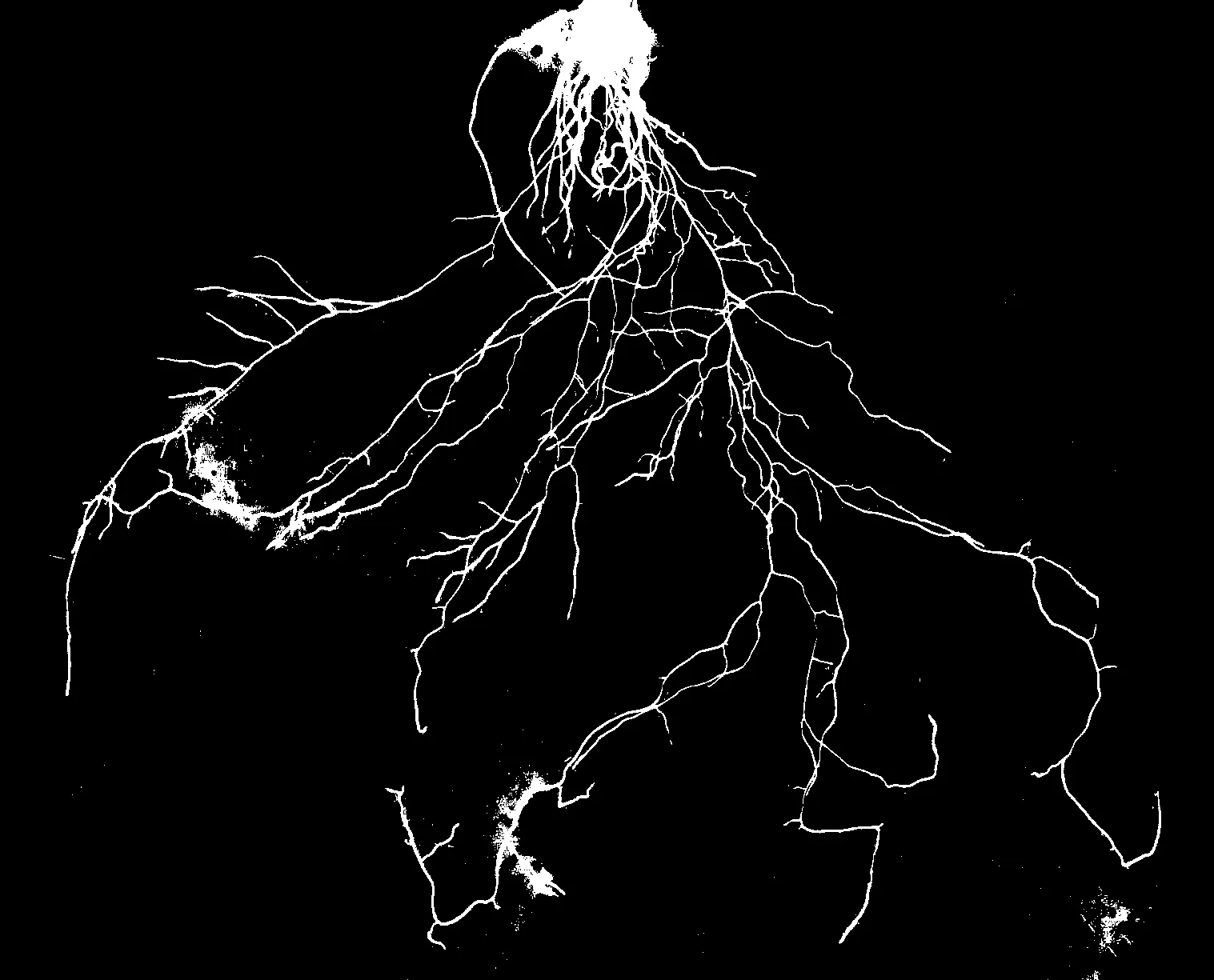
(b) 2号样本

(c) 3号样本

采用基于边缘分割[16-18]的LoG边缘检测器对小白菜根系样本图像进行边缘提取的结果(单像素轮廓图)如图6所示. 在图6(a)和6(c)中LoG边缘检测器取得了基本清晰的轮廓图, 但在图6(b)中可发现，该方法检测出了大量非边缘点的背景噪声. 由此可知, 尽管LoG边缘检测器能基本实现根系边缘的提取, 但算法稳定性较差, 对噪声及边缘模糊现象较为敏感. 除此之外, 由于小白菜根系图像边缘较弱, 该方法提取到的边缘点也存在大量断枝，出现不连续的现象.

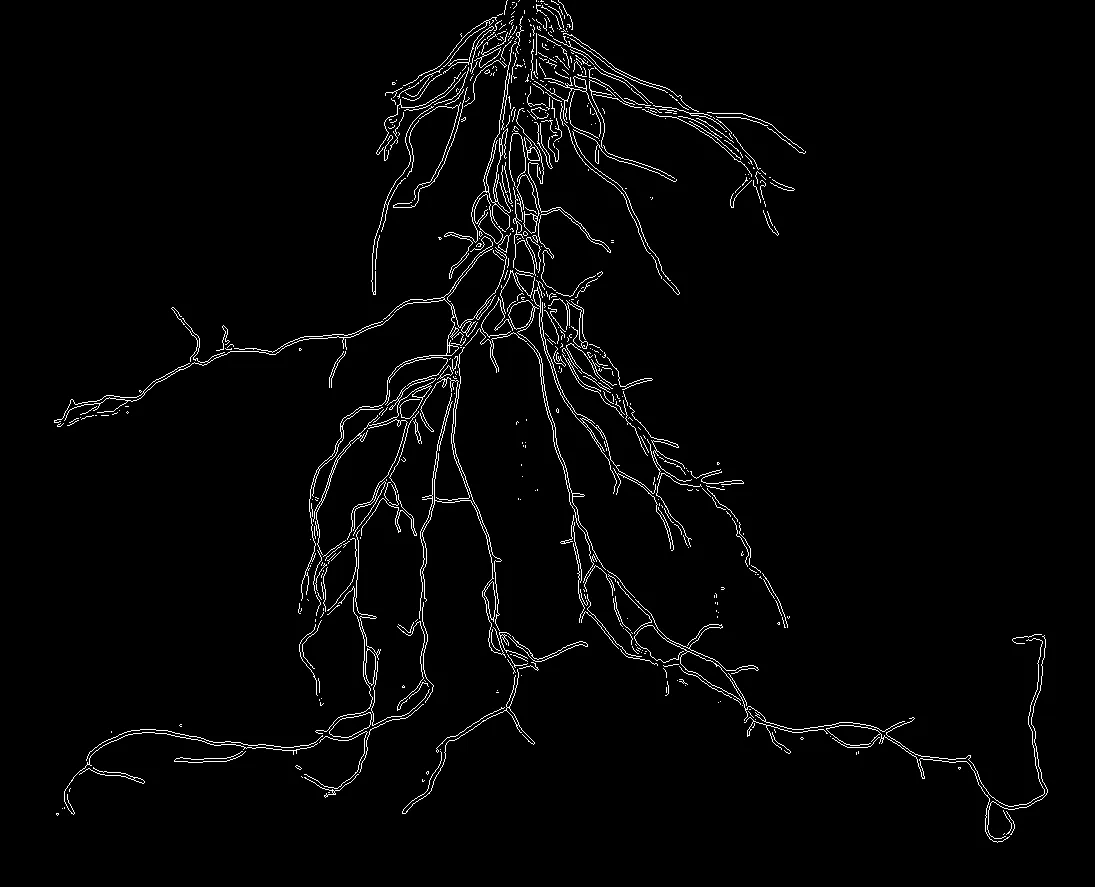
(a) 1号样本

(b) 2号样本

(c) 3号样本

采用基于区域分割的区域生长法[16]对小白菜根系样本图像进行分割处理的结果如图7所示.图7(a)可见区域中生长法同样取得了较好的分割效果, 但是在图7(b)和7(c)中同时出现了部分根系分支区域的过分割和欠分割现象. 其中，欠分割现象的产生是由于分支断裂而未能继续生长而分割出目标, 过分割则是由于灰度不均匀导致生长准则失效.

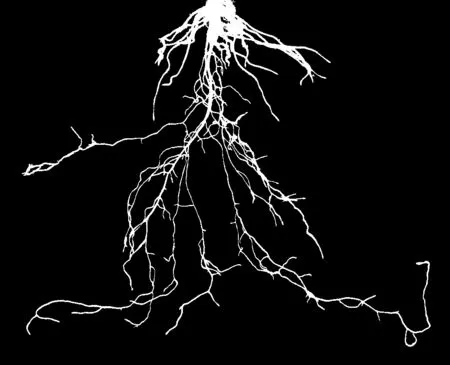
(a) 1号样本

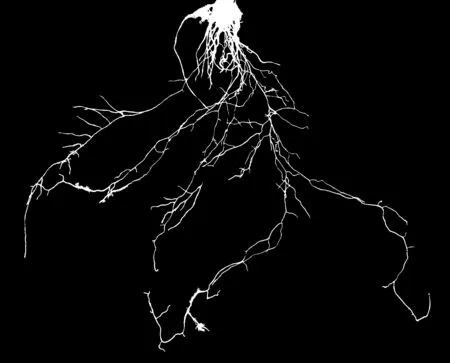
(b) 2号样本

(c) 3号样本

采用本文提出的叶菜根系图像分割算法对小白菜根系样本图像进行分割处理的结果如图8所示. 由图8(a)～8(c)可知, 本文提出的算法均取得了良好的分割效果. 1～3号样本的分割结果在噪声点、背景灰度不均匀处、根尖细节模糊处等区域均未出现过分割或欠分割现象. 由此可表明，本文算法对于背景灰度不均匀的叶菜根系弱边缘图像的分割有着更好的效果和稳定性.

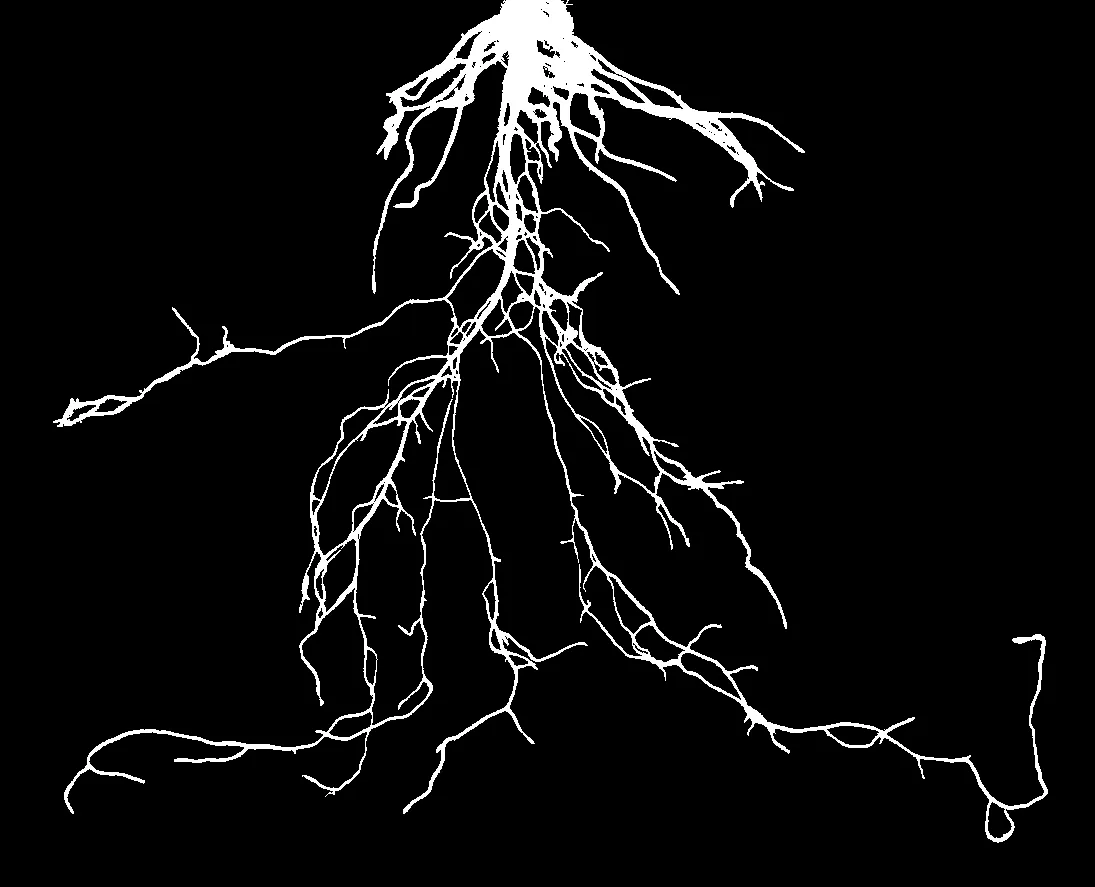
(a) 1号样本

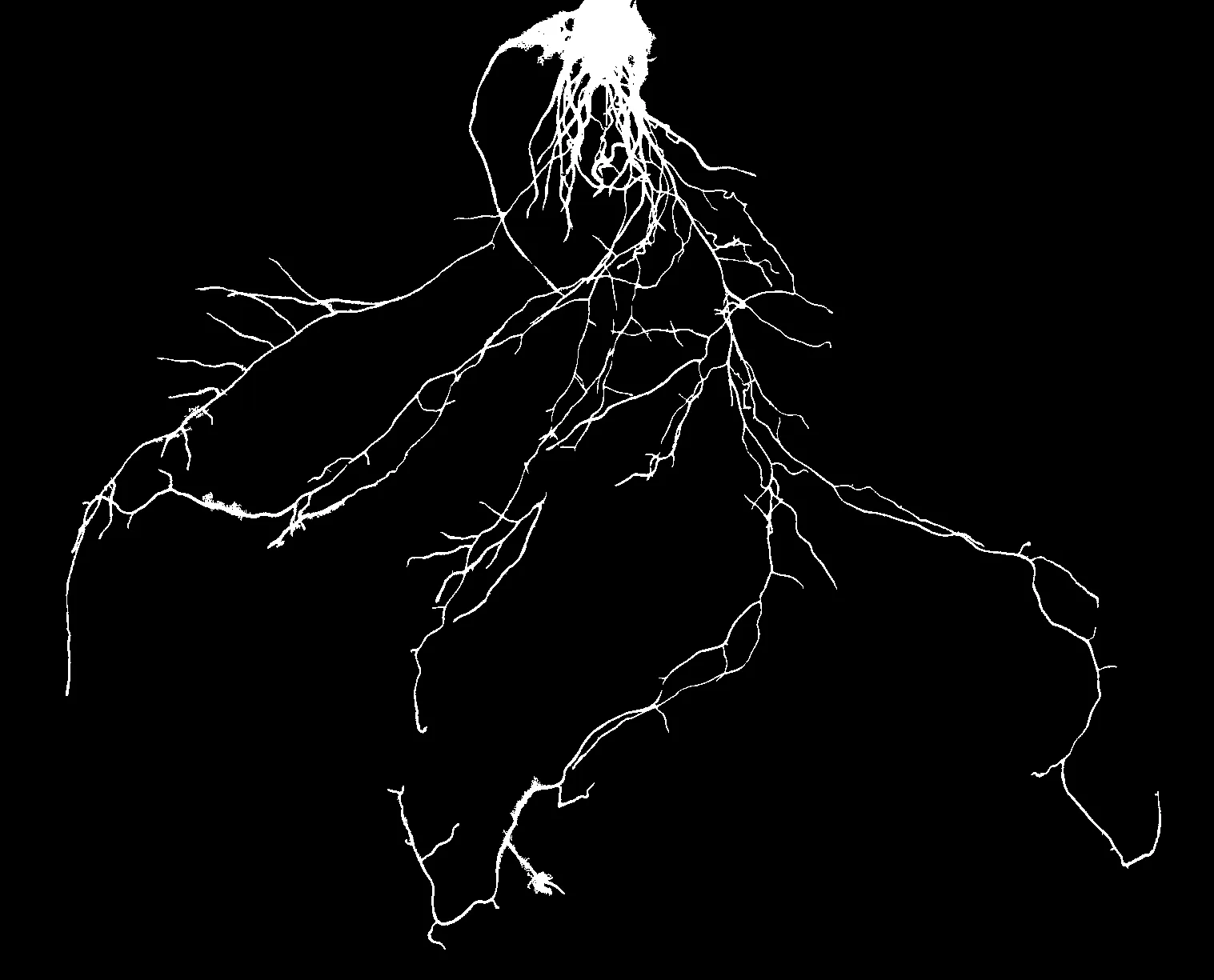
(b) 2号样本

(c) 3号样本

3 结 语

本文针对传统算法在叶菜根系弱边缘图像分割中效果不理想的问题, 展开了对变分水平集方法的研究, 设计了一种基于改进C-V模型的叶菜根系图像分割算法. 该算法保留了C-V模型对于处理弱边缘图像的适用性, 抗噪性能良好; 引入了Li模型中的符号距离保持项以避免周期性重复初始化水平集函数, 增加了算法演化的稳定性, 降低了对初始演化曲线的敏感性; 引入了图像的梯度信息, 改进曲线演化的进程从而能更好地处理叶菜根系图像中的局部灰度不均匀现象, 并在一定程度上提高了演化速度. 试验表明， 本文提出的基于改进C-V模型的叶菜根系图像分割算法有较好的分割精度和稳定性, 相比传统算法，其能更好地解决叶菜根系图像中弱边缘及局部灰度不均匀的问题.

[1] 宋文龙, 郭婧, 贾鹤鸣. 基于遗传BP网络的植物根系图像边缘检测[J]. 东北林业大学学报, 2011, 39(12): 121-123.

[2] 宋文龙, 闵昆龙, 邢奕, 等. 基于小波变换的自适应阈值植物根系图像边缘检测[J]. 北京科技大学学报, 2012, 34(8): 966-970.

[3] 朱鑫. 基于图像处理的植物根系分割及定量分析系统的研究与实现[D]. 重庆: 重庆大学计算机学院, 2014.

[4] OSHER S, SETHIAN J. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49.

[5] 朱湘君. 一种基于管状特征的水平集算法及其在医学图像血管分割中的应用[D]. 上海: 上海交通大学生命科学技术学院, 2009.

[6] 田杰, 胡秋霞, 马孝义. 基于高斯分布改进C-V模型的植物病斑彩色图像分割[J]. 农业工程学报, 2013, 29(16): 166-173.

[7] 周娟. 基于形状学习和曲线演化的医学图像分割研究[D]. 上海: 上海交通大学电子信息与电气工程学院, 2009.

[8] 薛维琴. 基于管状约束活动轮廓模型的血管分割方法研究[D]. 长春: 中国科学院研究生院长春光学精密机械与物理研究所, 2013.

[9] 何瑞英. 含边缘信息的C-V模型[J]. 计算机工程与应用, 2012, 48(18): 181-186.

[10] EPSTEIN C L, GAGE M. The curve shortening flow [M]. In Wave Motion: Theory, Modeling, and Computation: Springer-Verlag, 1987.

[11] KASS M, WITKIN A, TERZOPOULOS D. Snakes: Active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321-331.

[12] CASELLES V, CATTE F, COLL T, et al. A geometric model for active contours in image processing[J]. Numerische Mathematik, 1993, 66(1), 1-31.

[13] ADALSTEINSSON D, SETHIAN J A. A fast level set method for propagating interfaces[J]. J Comput Phys, 1995, 118(2): 269-277.

[14] CHAN T, VEST L, Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2), 266-277.

[15] LI C, XU C, GUI C, et al. Level set evolution without re-initialization: A new variational formulation[J].Computer Vision and Pattern Recognition, 2005, 1(1): 430-436

[16] GONZALEZ R C， WOODS R E. 数字图像处理[M].3版.阮秋琦，阮宇智，等译. 北京: 电子工业出版社, 2011: 450-496.

[17] CASTI P, MENCATTINI A, SALMERI M. Estimation of the breast skin-line in mammograms using multidirectional Gabor filters[J]. Computers in Biology and Medicine, 2013, 43(11): 1870-1881.

[18] JI R, QI L. Crop-row detection algorithm based on random hough transformation[J]. Mathematical and Computer Modelling, 2011, 54(3): 1016-1020.

(责任编辑:杨静)

SegmentationofLeafyVegetableRootImagesBasedonVariationalLevelSetMethod

FENGTairui1,MIAOYubin1,ZHUYunkai2,ZHAOShuang1

(1. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Xin Hua Hospital Affiliated to Shanghai Jiao Tong University School of Medicine, Shanghai 200092, China)

The segmentation of plant root image is the precondition of root feature extraction and analysis. In order to improve segmentation accuracy and stability in leafy vegetable root images with weak contour, a variational level set segmentation algorithm based on improved C-V(Chan-Vese) model was presented. The algorithm remained the applicability of C-V model to segmentation of images with weak contour, and moreover, it had been improved by introducing the image gradient information to solve the problem of grayscale non-uniformity. The validity of the algorithm was proved by segmenting root images of pakchoi cabbage. The results show that comparing with the traditional segmentation algorithms such as threshold method, Gaussian-Laplacian edge detector and region growing method, the presented algorithm can better solve the problems of weak contour and grayscale non-uniformity and achieve better segmentation precision and robustness. Variational level set method can be applied in leafy vegetable root observing and measuring system to effectively improve the system precision.

leafy vegetable roots; image segmentation; variational level set method; C-V model

TP 391.41

A

1671-0444 (2017)04-0552-07

2017-04-05

上海市科研计划资助项目(16391901700)；上海市卫生局青年课题资助项目(20134y038);上海交通大学医工交叉课题资助项目(YG2013MS15)

冯太锐(1994—)，男，安徽蚌埠人，硕士研究生，研究方向为机器视觉与数字图像处理. E-mail: fengtairui@sjtu.edu.cn

苗玉彬(联系人)，男，副教授，E-mail: ybmiao@sjtu.edu.cn