一种基于NFP非凸几何的船舶中间产品堆场布局优化方法

申兴旺， 鲍劲松， 王 越， 殷士勇

(东华大学 机械工程学院， 上海 201620)

一种基于NFP非凸几何的船舶中间产品堆场布局优化方法

申兴旺， 鲍劲松， 王 越， 殷士勇

(东华大学 机械工程学院， 上海 201620)

针对现代船舶制造过程中堆场空间资源浪费和布局不合理的现状，提出了一种基于NFP(no-fit polygon)非凸几何的船舶中间产品堆场布局优化方法.该方法以不规则多边形来表示结构件轮廓，将非凸多边形分割处理为简单凸多边形，用遗传算法对结构件在堆场中的排序进行优化.通过计算NFP实现船舶中间产品堆场的布局优化，解决非凸几何结构件在堆场中的布局问题. 试验结果表明，该方法可以有效提高船舶中间产品堆场的空间资源利用率.

船舶中间产品； 堆场布局优化； 非凸几何； NFP； 遗传算法

在当前船舶制造的模式结构中，大多数船舶建造是将中间产品作为生产的基本单元.由于结构件数量众多、形状不一且尺寸较大，通常在建造车间将中间产品建造成型后，经过各种制造工艺在船台将其合拢为整船，再对整船进行一系列整修工作，才算完成整个建造流程. 由于船体较为庞大，中间产品的体积和质量也较大，超过了一般车间生产的工件，而且在建造和存放的过程中不能叠放中间产品，故而这些中间产品在成型和合拢这两步中要占用很大的场地空间，这种划分出来临时放置中间产品的区域即称为“堆场”.

随着造船工艺水平的不断提高和建造规模的不断扩大，中间产品的堆场空间资源紧缺和堆场布局不合理已成为影响船舶建造生产效率的重要因素. 针对实际生产过程中存在的这一问题，研究船舶堆场布局的优化方法是非常必要的.但这一问题较为复杂，不同生产过程的约束条件也大不相同，导致堆场结构件在布局中无法达到最优. 堆场的布局问题可以简化为排样问题，以结构件的形状作为切入点，通过不规则多边形解出其临界多边形(no-fit polygon， NFP)来解决排样这一类问题. 目前，所采用的大多数NFP方法只能计算两个凸多边形的NFP，而非凸几何形状的NFP问题尚未得到解决. 在实际的船舶建造过程中，中间产品堆场中的结构件形状不规则，存在一些非凸几何形状的结构件，增加了堆场布局的难度. 假如能对这些非凸结构件进行更为合理的摆放，这对提高船舶中间产品的堆场空间资源利用率以及减少资源浪费将是十分有利的.

文献[1-2]针对二维不规则形状的排样问题做出了大量说明，同时指出对于此类问题的解决，NFP方法和遗传算法是一个非常重要的研究方向. Song等[3]对建造过程进行了分块，将场地布局放在了重要位置，并提出一种在初级阶段进行场地布局的综合方法，但这种方法的场地利用率不高.Caprace等[4]将三维布局问题简化为三维装箱问题，运用启发式算法对空间进行分配与调度优化.为了对不规则排样进行简化，将不规则多边形转化为矩形，使用最小包络矩形算法进行排样[5]，但该算法在包络时会产生大量空白区域.文献[6]在最小矩形包络算法的基础上研究了多边形两两组合的算法，该方法能有效提高板材利用率，但比较复杂，计算量较大.张志英等[7]通过最小包络多边形的方法，将复杂的分段形状进行最小包络处理.王蕾等[8]运用了网格划分法，将中间产品和堆场场地进行网格划分，并使用0-1矩阵来描述分段所占的场地空间，从而完成优化过程.文献[9-10]提出了基于遗传算法的排样方法，此方法的质量不高，效率尚待提高. 张志英等[11]对粒子群算法进行了改进，优化了中间产品调度序列，效果良好.马少辉等[12]从遗传算法出发，对调度序列进一步优化，并进行了算法验证，其利用率尚有提升空间. 纵观国内外研究现状，NFP方法在解决排样问题方面的应用很多，但将其结合遗传算法应用于中间产品堆场布局优化中的研究很少，将这种方法加以改进和优化，可以有效解决船舶中间产品堆场空间资源利用率低下的问题.

1 问题提出

1.1问题的描述

目前，针对堆场布局优化的研究还比较少，主要是由于船舶堆场中的约束条件众多，优化过程相对复杂，且效果不明显. 对中间产品堆场中存放的不规则结构件进行合理布局设计，首先可以忽略三维结构件的高度信息，投影到二维平面中，简化为二维排样问题，从而降低研究难度. 对于形状较为规则的结构件的优化已达到一定程度，而对于形状不规则尤其是非凸几何的结构件，由于布局过程较为复杂，优化效果不太理想，还存在一定的提升空间，因此具有较大的研究价值. 对于此类结构件，可以采用求解其NFP方法来进行处理.

NFP的研究已有几十年了，其对于解决不规则的几何多边形的碰撞重叠问题而言是一个很有效的方法. NFP的概念最先是由Albano和Sapuppo[13]提出的，它很好地确定了两个多边形的相对位置关系，而且对两个不规则的多边形提供了一系列的可能位置，这些位置之间正好接触而不会重叠. NFP方法在许多图形处理的相关领域都得到了很好的应用，也可用于堆场布局优化，以解决不规则形状结构件的摆放问题.

对于两个不同的多边形A和B，它们之间的NFP(简写为NFPAB)可以作如下定义：多边形A是固定住的，然后在多边形B上选择出一个参考点P，确定一个初始位置，将多边形B沿着多边形A做环绕一周的运动. 在环绕过程中，多边形B上至少需要有一点和A的边保持一个正好接触的状态，在此过程中多边形B不能进行旋转操作. 其中，在多边形B上选择的参考点P环绕一圈的运行轨迹就称为NFPAB，即多边形B相对于A位置的临界多边形. NFP的生成过程如图1所示，两个多边形始终保持恰好接触但不重叠.

1.2非凸多边形的NFP处理

对于非凸几何多边形NFP处理，目前多采用分割法，即将非凸多边形做凸化处理，简单来说就是将其分割为凸多边形. 在进行分割处理后，多边形的个数越少，复杂度将会越低，计算效率会越高. 本文所采用的凸化处理方法如下所述：从非凸多边形的一个顶点开始，沿着一个方向依次判断这个顶点是否为凹点，并进行记录，直到把所有顶点判断完毕；然后将第一个凹点和第二个凹点相连接之后做分割，第三个凹点和第四个相连，依次进行分割直到最后一个凹点. 若此非凸多边形只存在唯一的凹点，则取此凹点较近的一个对角线进行分割，最终使其凸化. 如果凹点的数目为大于1的奇数，则将最后一个凹点与第一个凹点相连接进行分割. 然而，经过第一次的凹点处理分割之后，特殊情况下可能仍存在凹点(例如图2，连接P2和P5进行分割之后明显还有凹点P2).对于这种情况，需要做进一步的处理，即需要重新查看每个分割后的多边形是否还有凹点，然后重复之前的步骤，从而可将非凸多边形完全分割为凸多边形.

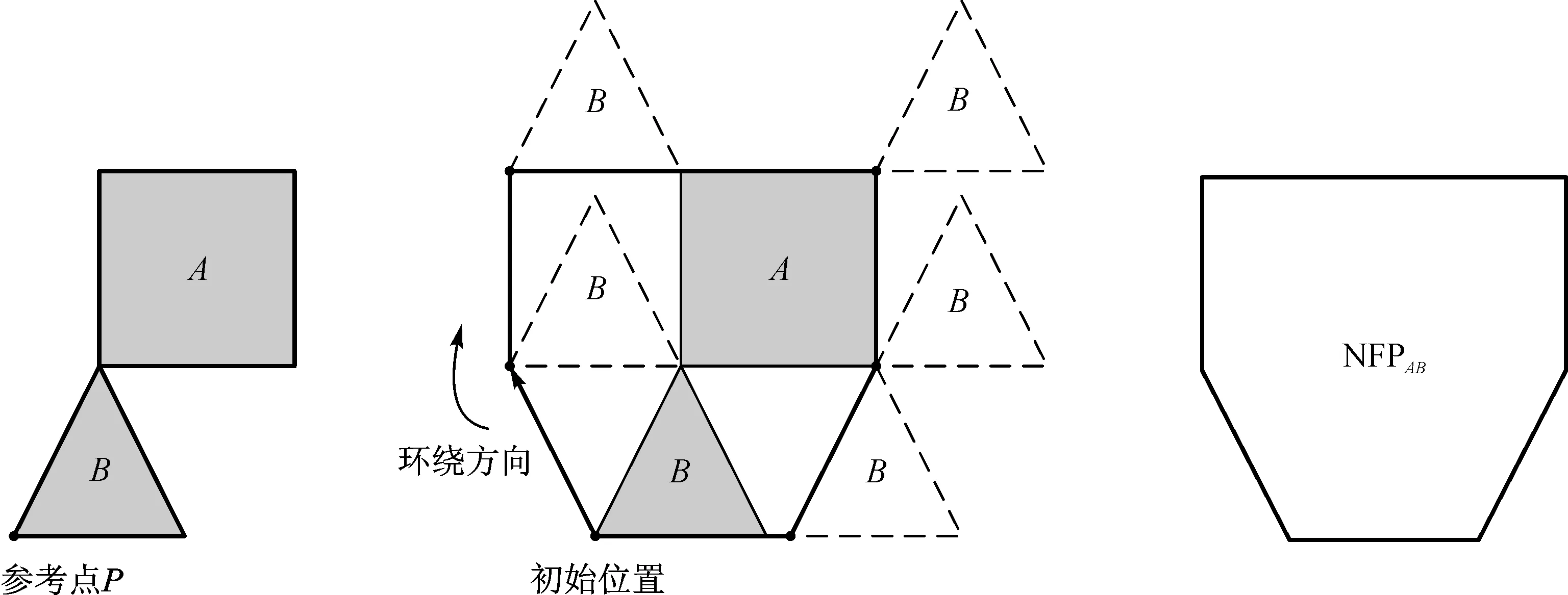
图1 NFP生成过程示意图Fig.1 The illustration of creating NFP

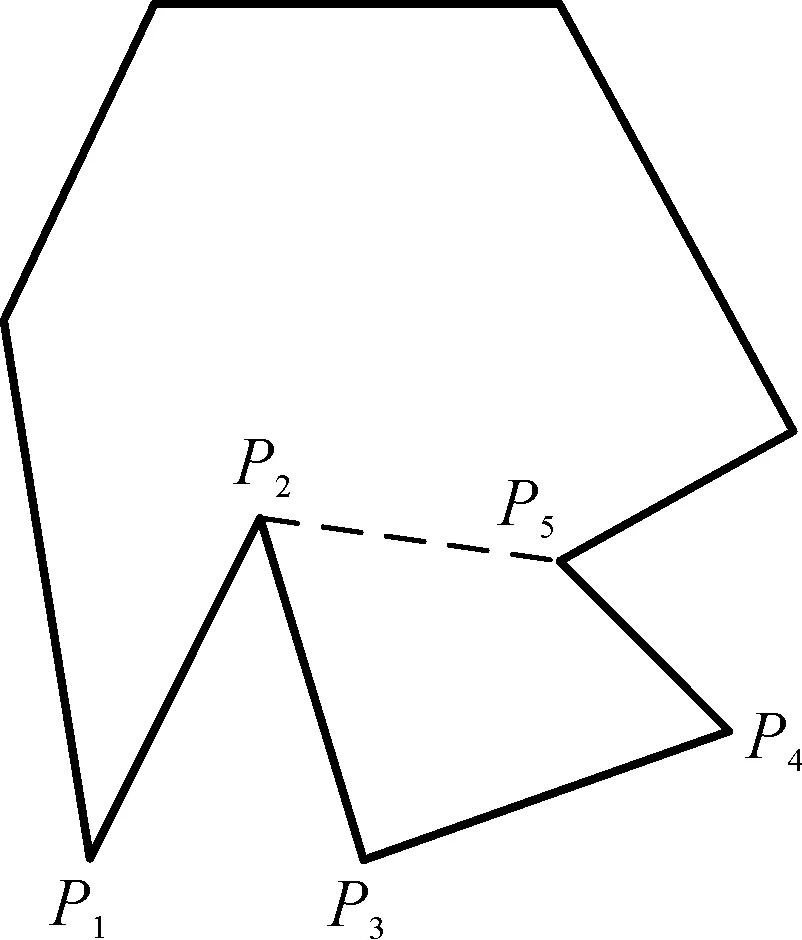
图2 相邻凹点分割过程Fig.2 Splitting process of the polygon with nearby concave points

1.3基于NFP的堆场布局描述

在排样问题当中，NFP可以给出接触但不重叠的可能位置，这已成为一种处理二维不规则多边形的基本方法. 同样地，NFP方法也可以应用于堆场布局问题. 对于堆场中形状不规则的结构件，尤其是非凸几何形状的多边形，其给堆场布局优化带来了很大难度，非凸的部分空间不能被利用，从而造成空间资源浪费，若能对这些空间合理布局，则利用率将得到提升. 具体处理过程是：首先判断是否为非凸几何形状，若是，则进行上文的凸化处理，分割为凸多边形；其次计算两个结构件的NFP，以保证两个结构件在堆场中不重叠，依次计算随后放入的结构件与之前多边形的NFP，直到所有结构件放入为止. 对于计算出的NFP，确定其所占面积足够小，这样布局出来的结构件就可以占用更小的空间，相当于提高了堆场空间的利用率. 将NFP方法运用于堆场布局过程，这种处理方法是十分有效的，也有利于提高船舶建造的生产效率.

2 基于GA的NFP堆场布局优化方法

2.1结构件编码方法

我曾经也为生在偏僻的农村而感到命运不公，力不从心，总是在困境中苦苦挣扎。在读书的时候，当我看到班上城市同学身上那种优越感，也曾失落过。

一条染色体代表一种布局方案，在进行染色体编码设计时，采用十进制编码，将待布局结构件的顺序号作为染色体的编码. 假设待布局结构件有9个，则随机选择的其中一条染色体编码可为<6， 2， 3， 9， 5， 1， 8， 4， 7>.

2.2适应度函数

设计适应度函数时采用以结构件的布局顺序进行堆场布局，将布局后的总面积利用率作为评价染色体的适应度，即适应度函数如式(1)所示.

(1)

式中:Ai为第i个已布局结构件的面积；Ay为需要进行布局的堆场面积；n为已布局结构件的个数.

2.3选择算子

设种群规模为M，在某一代种群中，它的第i条染色体的适应度值为fi，则该种群中所有个体的适应度如式(2)所示.

(2)

将fi所占F的比例组成一个轮盘，随机转动来进行轮盘区域的选择，轮盘的指针落在fi所占的区域，则选中此染色体i.

2.4交叉与变异算子

交叉算子采用线性顺序交叉方法(linear-order crossover， LOX)来实现交叉过程，该方法的优点是对染色体片段间的相对位置可较好保留. 两条染色体的交叉过程如图3所示.

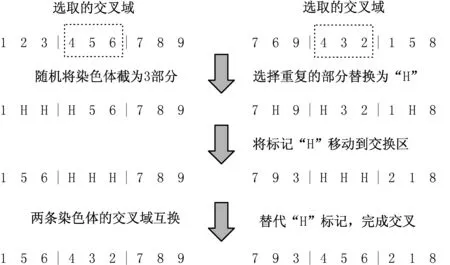
图3 两条染色体的交叉过程Fig.3 The crossover process of two chromosomes

变异的操作：随机选取染色体中的两个互不相同的位置，对这两个位置的数字进行交换完成变异操作.对于<6， 2， 3， 9， 5， 1， 8， 4， 7>这条染色体，互换第二个和最后一个位置，则变异之后的染色体变为<6， 7， 3， 9， 5， 1， 8， 4， 2>.

2.5堆场布局优化过程

对船舶的中间产品堆场进行布局优化，将结构件放入堆场中进行摆放，使得堆场的空间资源利用率达到最优. 在堆场布局优化过程中，可按照如下步骤来完成.(1)对结构件进行预处理，将不规则的几何形状(包括非凸几何多边形)转化为简单多边形；(2)通过使用遗传算法，对堆场布局进行优化，产生一个接近最优的结构件摆放顺序，这一步非常重要，摆放次序的合理与否对堆场的空间利用率产生直接影响；(3)将摆放顺序中的第一个结构件摆放于堆场中，并根据左下原则置于堆场的左下角，然后按顺序取第二个结构件，并计算出这两个结构件之间的NFP；(4)对NFP上的位置是否最优进行评估，计算上步得到的NFP面积，使其尽量小，确定最优的布局摆放方法；(5)对前两个结构件进行整理优化，合成一个新的多边形，再计算第三个结构件与新的多边形之间的NFP；(6)继续按顺序取下一个结构件，重复上述过程直到在堆场中将所有结构件摆放完毕.

本文所用的NFP方法进行堆场布局优化过程如图4所示.

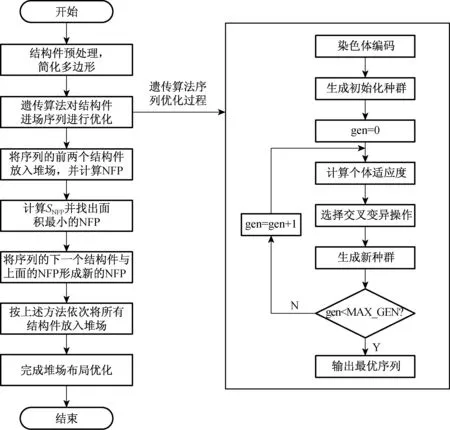
图4 堆场布局优化过程Fig.4 The process of yard layout optimization

3 试验与分析

为证明本文所述堆场布局优化方法的有效性，通过以下实例进行验证. 选取一个矩形堆场空间，将实际生产过程中的几个船舶中间产品放入堆场中，进行堆场布局，首要保证所有中间产品均能放入堆场中，如图5所示，有9个中间产品将要放入堆场中.

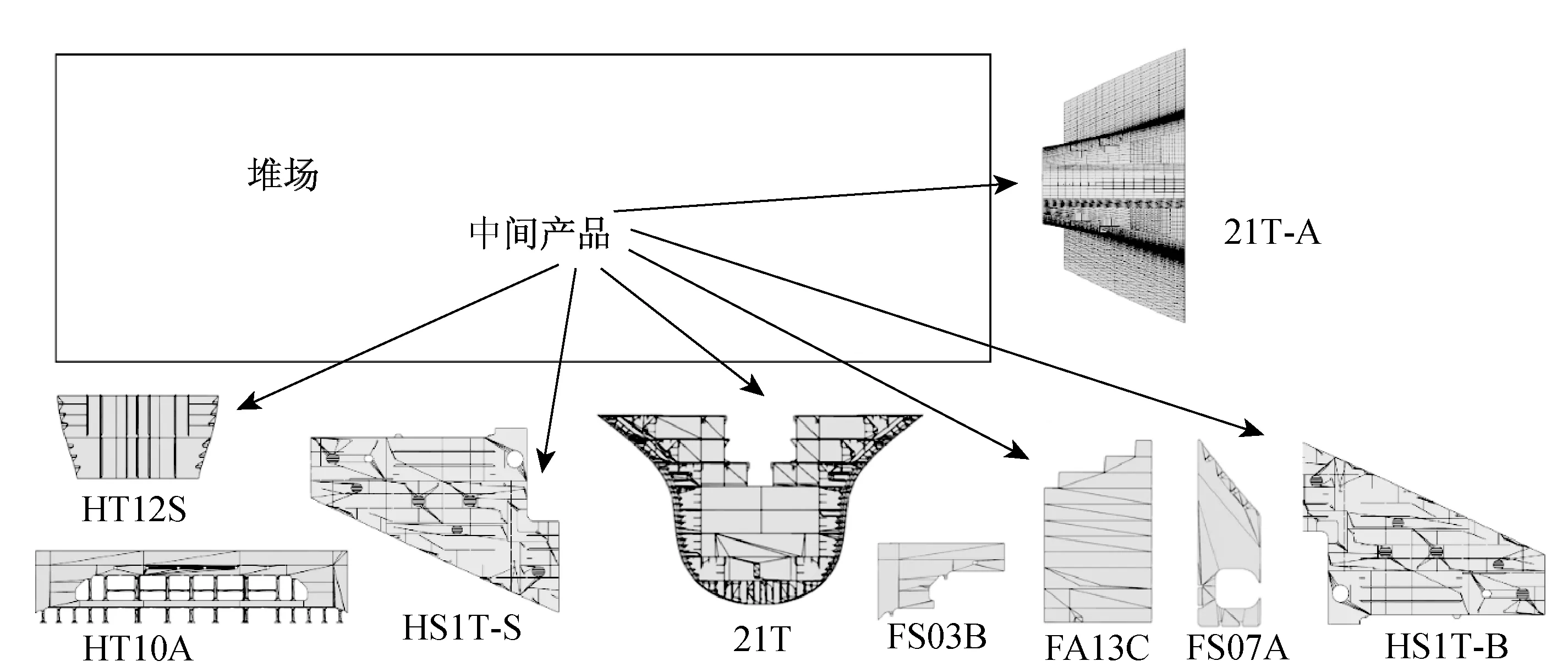
图5 中间产品放入堆场示意图Fig.5 The illustration of allocating intermediate products into a yard

方法1：采用最小包络矩形法，布局优化结果如图6所示.

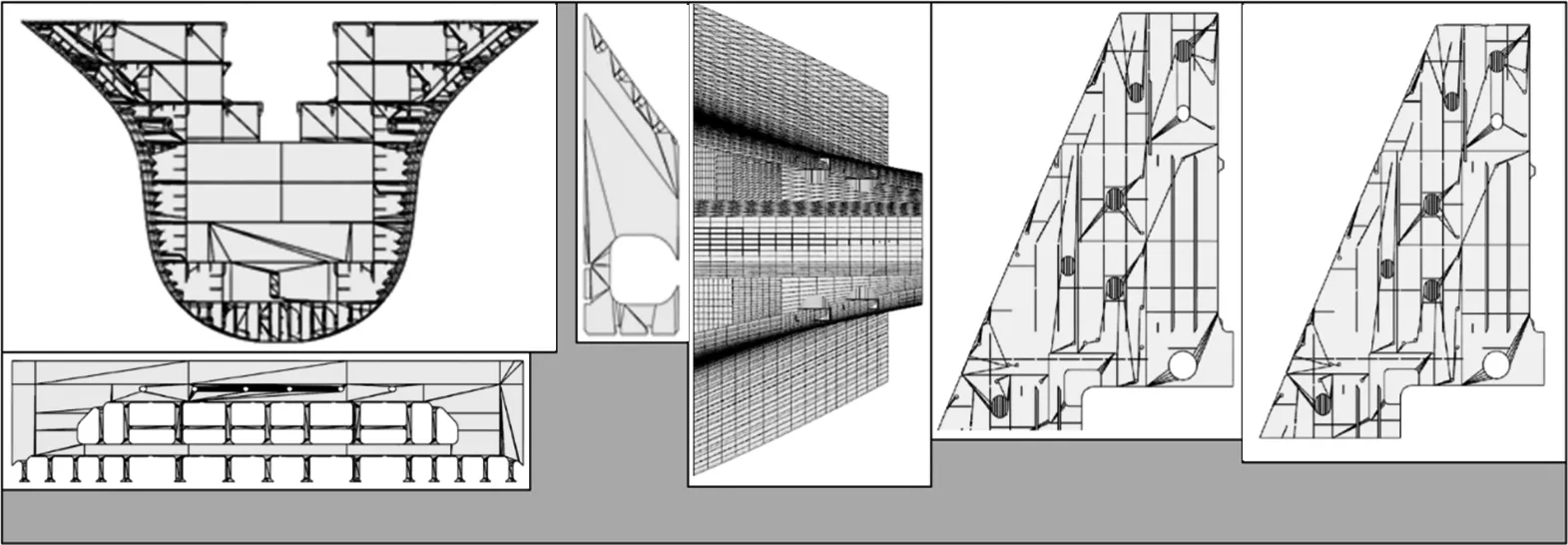
图6 最小包络矩形法布局优化结果Fig.6 The improved layout result by minimum envelope rectangle

方法2：采用只考虑凸多边形的方法，布局优化结果如图7所示.

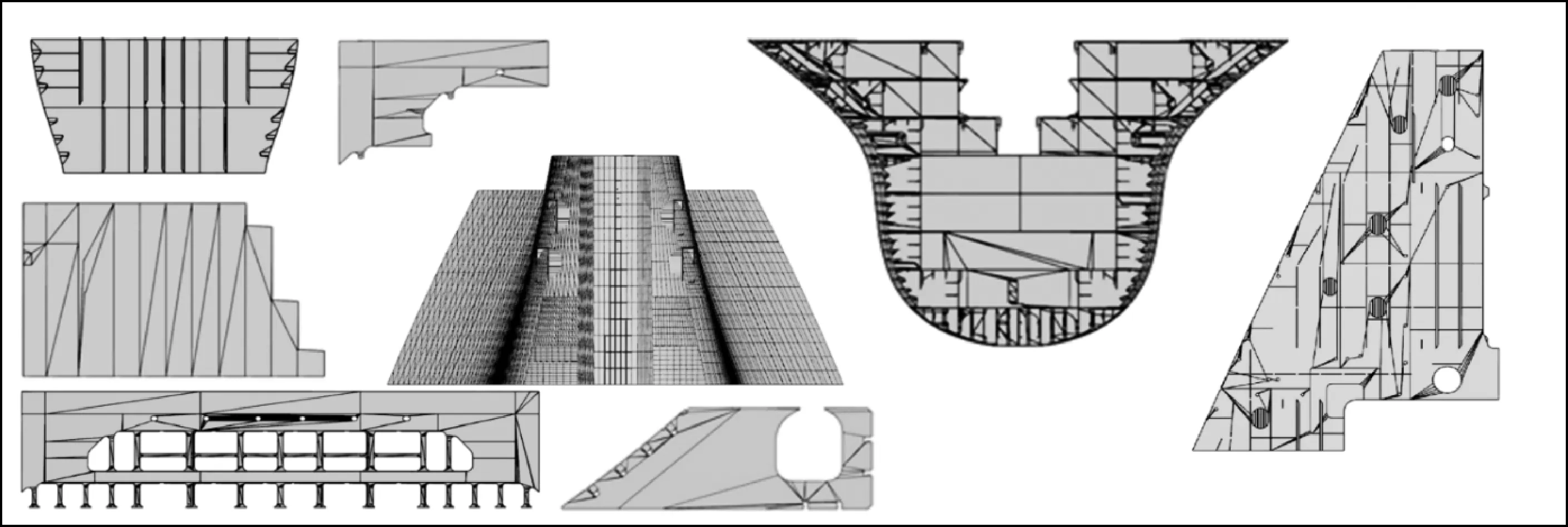
图7 只考虑凸多边形的布局优化结果Fig.7 The improved layout result only concerning convex polygons

方法3：采用考虑非凸多边形的方法，布局优化结果如图8所示.

上述3种方法的布局结果分析如表1所示.

表1 布局结果对比

从表1可以看出，方法3在堆场空间利用率上得到了大幅提升. 相对于方法1，最小包络矩形处理过程简单，但对于大尺寸不规则结构件，包络矩形中的边角空间有很大浪费，空间利用率不高. 方法2的空间利用率要稍好一些，处理过程相对方法3简单，但未能对非凸多边形合理利用. 方法3将非凸多边形凸化处理，用遗传算法对布局的结构件序列进行优化，得到了合理的堆场布局，空间利用率大大提升. 由案例分析发现，基于NFP的非凸几何将对堆场布局优化过程产生重大影响，合理解决会对空间资源紧缺的船舶堆场提供帮助.

4 结 语

本文对非凸几何形状的结构件在船舶中间产品堆场中的布局优化提供了一种解决方法，通过计算不规则多边形的NFP，在保证不重叠的基础上将结构件在堆场中进行合理放置.通过遗传算法对结构件的放置顺序进行优化，从而达到在满足布局要求的情况下提高场地利用率的目的. 采用实例进行分析验证，通过与其他方法比较可以发现，本方法的堆场空间利用率比最小包络矩形法和仅考虑凸多边形的高，且可以在堆场中放入更多的结构件. 合理利用非凸几何，对进一步提高堆场空间利用率和布局的最优化具有显著影响. 但该方法的计算效率尚待加强，暂不能应对大规模的场景，否则会显著影响效率.同时本文提出的方法在验证过程中缺少约束，情景环境较为理想，实际上这些约束因素会对真实的堆场布局过程造成影响，后续研究将从这方面着手，进一步提高本方法的实用性和计算效率.

[1] HOPPER E，TURTON H. A review of the application of meta-heuristic algorithms to 2D strip packing problems[J]. Artificial Intelligence Review， 2001，16(4)： 257-300.

[2] KATHRYN A D， WILLIAM B D. Solution approaches to irregular nesting problems [J]. European Journal of Operational Research， 1995，84(3)：506-521.

[3] SONG Y J， WOO J H. New shipyard layout design for the preliminary phase & case study for the green field project[J]. International Journal of Naval Architecture and Ocean Engineering， 2013， 5(1)： 132-146.

[4] CAPRACE J D， PETCU C， VELARDE M G. Optimization of shipyard space allocation and scheduling using a heuristic algorithm [J]. Journal of Marine Science and Technology， 2013，18(3)：404-417.

[5] 陈小雨.二维不规则零件自动优化排样算法的研究[D].哈尔滨：哈尔滨理工大学计算机科学与技术学院，2012.

[6] ELKERAN A. A new approach for sheet nesting problem using guided cuckoo search and pairwise clustering[J]. European Journal of Operational Research， 2013，231(3)：757-769.

[7] 张志英，杨克开，于瑾维.面向船体分段建造的二维不规则空间调度方法[J].上海交通大学学报，2012，46(4)：651-656.

[8] 王蕾，张志英.基于规则的船体曲面分段空间调度方法[J].上海交通大学学报，2009，43(11)：1709-1714.

[9] FISCHER A D， DAG L H. Employing subgroup evolution for irregular-shape nesting[J]. Journal of Intelligent Manufacturing， 2004，15(2)：187-199.

[10] FRANCIS E， TAY H， CHONG T Y. Pattern nesting on irregular-shaped stock using genetic algorithms[J]. Engineering Applications of Artificial Intelligence，2002， 15(6)：551-558.

[11] 张志英，杨克开，于瑾维，等.改进粒子群算法的动态空间调度方法[J].哈尔滨工程大学学报，2009，30(12)：1344-1350.

[12] 马少辉，王景秋，陆春霞，等.动态空间调度的混合遗传算法[J].运筹与管理，2013，22(2)：99-104.

[13] ALBANO A， SAPUPPO G. Optimal allocation of two-dimensional irregular shapes using heuristic search methods[J]. Systems， Man and Cybernetics， IEEE Transactions on， 1980， 10(5)： 242-248.

(责任编辑：杜佳)

AMethodforImprovingtheYardLayoutofNon-convexGeometryShipbuildingIntermediateProductsBasedonNFP

SHENXingwang，BAOJinsong，WANGYue，YINShiyong

(College of Mechanical Engineering， Donghua University， Shanghai 201620， China)

Aiming at the situation of the waste of yard space and unreasonable layout problems during modern shipbuilding process， an optimized method based on NFP(no-fit polygon) is proposed to improve the layout yard of concave intermediate shipbuilding products. This method represents the outlines of parts with irregular polygons， divides concave polygon into several simple convex polygons， uses genetic algorithm to improve the order of the parts， and optimizes the layout by calculating the NFP to resolve the layout problems of non-convex parts in a yard. The experimental results show that this method can efficiently elevate the utilization ratio of the space resources of the shipbuilding intermediate products yard.

shipbuilding intermediate products； yard layout optimization； non-convex geometry； NFP； genetic algorithm

TH 181

A

1671-0444 (2017)04-0478-06

2016-12-28

国家自然科学基金资助项目(51475301)

申兴旺(1992—)，男，河南林州人，硕士研究生，研究方向为智能制造与测控.E-mail：814457915@qq.com

鲍劲松(联系人)，男，副教授，E-mail：bao@dhu.edu.cn