一种基于最小二乘圆动态特征分析的圆度误差稳健评估方法①
2017-11-01曹志民吕秀丽宋鸿梅赵丽华
曹志民 吕秀丽 韩 建 吴 云 宋鸿梅 赵丽华
(1.东北石油大学 a.电子科学学院;b.博士后科研流动站;2.大庆油田博士后科研工作站)
一种基于最小二乘圆动态特征分析的圆度误差稳健评估方法①
曹志民1,2吕秀丽1a韩 建1a吴 云1a宋鸿梅1a赵丽华1a
(1.东北石油大学 a.电子科学学院;b.博士后科研流动站;2.大庆油田博士后科研工作站)
针对现有圆形工件圆度误差测量与评估方法大多仅从整圆全局的角度出发,而对局部圆度动态误差特性关注不足的问题,设计了一种基于局部最小二乘圆参数动态特征的工件圆度高稳健评估方法。首先,通过随机选取均匀分布的固定数目原始点进行初始圆参数拟合,在初始圆参数约束下对原始数据点进行划分;接下来,对每一个划分结合随机采样一致性(RANSAC)技术实现局部圆度参数的动态计算;最终在局部圆参数统计特征的支持下实现了局部和全局圆度误差的评估。实验结果表明:所提方法能够稳定有效地实现工件圆度的评估。
圆度 圆形工件 局部误差 RANSAC 最小二乘
随着仪器仪表和机械技术的飞速发展,现代自动化仪器仪表和机械产品的工艺复杂度越来越高。关键零件的性能对相关产品的性能和寿命至关重要,其中使用最多的基本零件是圆形和圆柱形,因此圆度(圆度形变)测量一直以来都是学术界的研究热点[1~3]。国际标准化组织ISO/TS针对圆度误差的表示问题[4,5]给出了4种常用的方法:最小二乘圆(Least Square Circle, LSC)、 最大内接圆(Maximum Inscribed Circle, MIC)、最小周长圆(Minimum Circumscribed Circle, MCC)和最小区域圆(Minimum Zone Circle,MZC)。
这4种方法分别通过构造标准参考圆,并利用实测数据与标准参考圆间峰值或谷值距离给出相应的误差表示。显然,4种常用的标准参考圆表示条件的圆度误差计算都属于一种全局误差表示,且这种误差对噪声和野值点非常敏感。实际应用中,除了关心工件截面整体圆度外,很多情况下需要对工件局部圆度误差进行测量和评估,进而可根据分析结果进行工件生产工艺和应用领域的改进、评估。显然,对于利用局部数据进行圆度评估问题,也需要通过给出类似参考圆的方法来实现,然而,以上4种方法中,只有最小二乘参考圆能够适应局部数据圆拟合,其他3种方法都无法给出局部数据参考圆的精确估计。而实际应用中,局部圆度偏差等缺陷往往对工件质量有着不可忽略的影响,如外套管件外压圆筒局部圆度偏差对局部弯曲应力的影响等[6]。针对这一问题,笔者提出了一种基于最小二乘圆动态特征分析的(局部)圆度误差测量和评估方法。
1 最小二乘圆度测量方法
1.1 最小二乘法原理
数据拟合或参数估计问题一般可以转化为最小二乘拟合或估计问题[7,8]。最小二乘问题是数学中的一种逼近优化方法[9]。对于具有如下关系的物理模型:
y=f(z;x1,x2,…,xn)
(1)
其中f是一个由参数x1,x2,…,xn定义的期望函数,z为控制变量或数据,y是关于数据z和模型参数x1,x2,…,xn的期望输出。经过m次测量(m≥n),可以得到m组观测数据(zi,yi)(i=1,2, …,m)。由于测量误差或噪声的存在,观测数据(zi,yi)不一定完全满足期望函数(1)。为此,期望通过调整参数x1,x2,…,xn来实现如下目标函数的最小化:

(2)
式(2)最小化的一个必要条件是▽g(x1,x2,…,xn)=0。根据期望函数的不同,最小二乘问题可分为线性最小二乘和非线性最小二乘问题。对于线性最小二乘问题,有:
f(z;x1,x2,…,xn)=x1zn-1+…+xn-1z+xn
(3)
那么,对应的最小二乘问题的观测方程为:
(4)
其中,[ε1,ε2,…,εm]T为期望模型的误差向量。一般的,式(4)为一个超定方程组,写成矩阵形式为:Ax=b+ε。那么,最小二乘拟合或估计问题最终形式可描述为如下最优化问题:
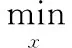
(5)
在矩阵A满秩的情况下,参数向量的解析解x=(ATA)-1ATb。
对于非线性最小二乘问题来说,可结合必要
条件▽g(x1,x2,…,xn)=0完成最小二乘问题的求解。
1.2 最小二乘圆
由以上分析可知,最小二乘拟合需要确定期望函数,最终求解相关参数。对于圆拟合,需要通过一系列的数据点坐标(ui,vi)来拟合如下二维圆方程:
(ui-uo)2+(v-vo)2=r2
(6)
f((x,y);xo,yo,r)=x2+y2+xo2+yo2-2xxo-2yyo-r2
(7)
对应的最小化目标函数为:
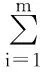
(8)
令α=r2,最小化目标函数为:
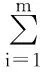
(9)
取g(xo,yo, α)对α的偏导数,有:

(10)
即:
(11)
取g(xo,yo,α)对xo的偏导数,有:


(12)
即:
(13)
同理,取g(xo,yo, α)对yo的偏导数可得:
(14)
式(13)展开后有:

(15)
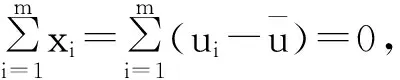
(16)
同理,有:
(17)

(18)
2 基于最小二乘圆动态特征分析的局部圆度评价
在可能存在野值点和噪声的情况下,笔者结合随机采样一致性(RANdom Sampling and Consensus, RANSAC)技术进行局部圆度拟合,并记录相应的圆参数,最终利用最小二乘圆拟合方法进行(局部)圆度评价,在给出目标整体圆度评价的基础上同时给出局部圆度动态变化情况等细节信息。具体的算法步骤如下:

b. 初始化参考圆个数为Nc=0和参考圆参数向量为空集。
c. 利用样本点关于初始参考圆圆心的角度信息将数据点分为N等份 (N的选择需要保证每份不能少于k1个点)。

3 实验结果与分析
为了验证笔者算法的有效性,采用了两组典型的圆度测试数据集[10,11],如图1所示。

图1 实验采用的两组数据集
对以上两组数据集分别计算了4种标准参考圆下的圆度误差和笔者所提算法给出的两种基于局部最小二乘圆动态特征的圆度误差,图2给出了笔者算法得到的局部最小二乘圆参数直方图,最终实验结果见表1、2(其中笔者方法给出的圆参数为所有局部最小二乘圆参数的均值)。

图2 两组数据局部最小二乘参数直方图

参数LSCMICMCCMZC笔者方法uc/mm0.02420.0066-0.00570.00540.1451vc/mm0.00770.00280.00770.0079-0.1041r/mm1.43961.01431.9641-1.4812圆度误差0.96180.05850.96240.9574Epv:2.5575Estew:0.5132

表2 数据集2的圆度误差测量结果对比
由图2可知,圆度测量数据的局部确实存在较大变动,需要进行局部圆度的动态参数测量。从表1、2的最终圆度误差测量结果中可以看到,通过笔者方法进行的圆度误差测量除了能够体现局部参数动态变化外,还能很好地给出圆度参数计算和圆度误差评估。
4 结束语
针对工业生产中复杂环境下圆形工件圆度测量的局部误差测量需要,通过对测量数据进行局部最小二乘圆拟合并记录局部拟合圆参数变化情况,设计了基于局部最小二乘圆动态特征的圆度测量和评估方法。通过对不同测量误差分布特征的测量数据进行的圆度误差测量实验,验证了笔者方法的有效性,为复杂工业生产环境下圆形工件圆度测量和评估提供了一种稳定有效的方法。
[1] 罗钧,林于晴,刘学明,等.改进蜂群算法及其在圆度误差评定中的应用[J].机械工程学报,2016,52(16):27~32.
[2] 吴伟仁,姜黎,张之敬,等.以计算几何为基础的圆度误差评定方法[J].宇航学报,2012,33(6):816~822.
[3] 郑静娜,李红玉,郑斯文,等. 利用回溯搜索优化算法(BSA)测量圆度误差[J].辽宁大学学报(自然科学版),2015,42(4): 320~324.
[4] ISO/TS 12181-1,Geometrical Product Specifications (GPS)—Roundness,Part 1: Terms, Definitions and Parameters of Roundness[S]. Geneva:ISO, 2003.
[5] ISO/TS 12181-2,Geometrical Product Specifications (GPS)—Roundness,Part 2:Specification Operators[S].Geneva:ISO, 2003.
[6] 陈聪,王月,李玮,等.稳压器电加热元件外套管失稳分析[J].化工机械,2014,41(3): 327~331.
[7] Markovsky I,Huffel S V.Overview of Total Least-squares Methods[J].Signal Processing, 2007, 87(10): 2283~2302.
[8] Stoica P,Sodeerstrom T.Bias Correction in Least Squares Identification[J].International Journal of Control,1982, 35(3): 449~457.
[9] 索振鹏,宫爱玲.最小二乘法与灰度重心结合实现圆度检测[J].化工自动化及仪表,2016,43(9):910~912.
[10] Huang J.A New Strategy for Circularity Problems[J]. Precision Engineering, 2001, 25(4):301~308.
[11] Jywe W Y, Chen C K, Liu C H.The Min-Max Problem for Evaluating the Form Error of a Circle[J].Measurement,1999,26(4):273~282.
ARobustRoundnessErrorEvaluationMethodBasedonDynamicFeatureAnalysisofLeastSquareCircles
CAO Zhi-min1,2, LV Xiu-li1a, HAN Jian1a, WU Yun1a, SONG Hong-mei1a, ZHAO Li-hua1a
(1a.SchoolofElectronicScience; 1b.StationforPost-doctoralStudiesWork,NortheastPetroleumUniversity; 2.Post-doctoralResearchCenter,DaqingOilfield)
Considering the fact that existing circular workpieces’ roundness error measurement and evaluation mostly starts with a global manner for the measured circle and pay less attention to the dynamic error characteristics of local roundness, a robust roundness evaluation method for circular workpieces based on local least square circle fitting was proposed, in which, having equally-distributed initial points of fixed number selected randomly for parameter fitting and then having all data points divided into several local sections by employing initial entire circle parameters; and then for each local section, having random sampling and consensus (RANSAC) technology adopted to estimate dynamic local circle parameters and finally, having local and entire circle errors evaluated under the support of statistical feature of local circle parameters. Experiential results illustrate that the proposed method can stably perform robust roundness evaluation efficiently of the circular workpiece.
roundness,circular workpiece,local error, RANSAC,least square
国家自然科学基金项目(51374072)。
曹志民(1980-),讲师,从事图像/视频信号、石油勘探开发多源信号处理及模式识别等的研究,dahai0464@sina.com。
TH13
A
1000-3932(2017)06-0563-05
2016-11-26,
2017-05-04)
