像素自相关矩阵的阈值自适应角点检测算法

邓小炼，杜玉琪，王长耀，王晓花



像素自相关矩阵的阈值自适应角点检测算法

邓小炼1，杜玉琪1，王长耀2，王晓花1

（1. 三峡大学理学院，宜昌 443002； 2. 中国科学院遥感与数字地球研究所，北京 100101）

针对Harris角点检测算法中角点响应函数（corner response function，CRF）系数阈值与非极大值抑制系数阈值需要人为设定所造成的可变性和随机性等问题，该文提出一种通过计算图像每个像素的自相关矩阵行列式值，构造特征角点图像进行自适应阈值分割的改进Harris角点检测算法。该算法首先通过计算原图像经过方向滤波和低通滤波后各像素的自相关矩阵行列式值，以此构造特征角点图像；然后采用OTSU算法计算特征角点图像分割阈值，从而筛选出预选区域；最后结合改进的非极大值抑制方法提取有效角点。通过5组角点检测对比试验结果数据分析，不同类型图像的角点检测准确率均有提高，高分二号遥感影像的角点检测准确率提高27.06个百分点，可以初步得出，该算法相比传统Harris角点检测算法不但能够自动计算角点检测的最佳阈值，而且能够更准确地定位角点和去除边缘伪角点，从而提高了角点检测的精确度，该研究可为农业遥感影像数据检测提供参考。

图像处理；算法；角点检测；自相关矩阵；特征角点图像；非极大值抑制

0 引 言

角点通常是指图像中梯度值与梯度变化率都非常大的像素点以及图像边缘曲线曲率极大的像素点，它能反映出图像的局部特征，在降低信息数据量的同时有效地保留了图像的重要特征[1]。角点检测在目标识别[2]与跟踪、光流计算、图像配准[3]、相机标定、运动估计、三维测量[4]与重构等计算机视觉处理中发挥着极其重要的作用。此外，图像配准和镶嵌的自动化是农作物长势遥感监测和信息快速获取的关键技术之一；遥感变化检测技术也是耕地快速高效提取和动态监测方法的关键技术之一。因此，角点检测在农业信息化领域也发挥着极其关键作用。

目前，角点检测的方法主要分为两类：基于图像灰度信息的方法和基于图像边缘轮廓特征[5]的方法。前者主要通过计算曲率[6]及梯度进行角点检测，如SUSAN算法[7]，Harris算法[8-9]和Morevec算法[10]。而后者需要对图像预分割、轮廓链码提取和角点检测[11-12]3个步骤，如基于边界链码的角点检测[12-14]，基于边界曲率的角点检测[15]，基于边界小波变换的角点检测[16]。在基于图像灰度信息的方法中，Harris角点检测算法效果较为理想，在纹理较丰富的区域可提取大量特征点，对图像旋转、灰度变化、噪音和视点变换不敏感。众多学者在此基础上进行了改进，如赵萌等[17]提出一种针对高斯函数参数值自适应的Harris算法，但该算法需要在选定区域中设置多个值，并对不同值生成的预选角点响应函数采用约束准则筛选出最大值，算法较为复杂且运算时间较长；Mikolajczyk等[18]构建了具有尺寸不变的Harris-Laplace算子和仿射不变的Harris-affine算子；王玉珠等[19]应用B样条函数替代了Harris算法中的高斯函数；Gevrekic等[20]提出的方法改进了Harris算法在光照改变条件下的稳定性；龙中杰等[21]应用领域像素取差法和Susan去角点的特性改进Harris算法；毛雁明等[22]提出双阈值法解决了非极大值抑制时不易设置阈值的问题；李海等[23]使用直线检测算法来进行角点的自动提取，在进行非极大值抑制时回避了阈值设定；Mokhtarian等[24]提出CSS(curvature scale space)算法图像进行几何变换时相当稳定，在多尺度空间下也能具有很好的鲁棒性；Awrangjeb等[25]提出了基于CPDA(chord-point distance accumulation)角点检测算法，采用点到弦距离累加CPDA来代替曲率的计算；周志艳等[26]提出的Harris角点检测算法针对角点响应函数进行改进，然而图像灰度标准差的选择对角点的数量以及角点的匹配精度具有很大的影响。

本文针对Harris算法中角点响应函数系数阈值和非极大值抑制系数阈值的设定具有很大的随机性和动态可变性，容易造成角点检测效果不理想，因此提出一种新的思路：直接利用图像像素的自相关矩阵计算得出特征角点图像，之后进行自适应的阈值分割，并采用改进的非极大值抑制方法对预筛选结果进行处理，最终检测出具有较高定位精度的最佳角点。此外，除了常见的JPG、BMP等图像格式之外，本文改进算法更适用于遥感多光谱影像，因为遥感影像的波段数较多，图像特征相比通用图像格式更多，可以反映出更多的在可见光波段无法反映的地物光谱特征，因此更有利于角点检测。

1 Harris角点检测原理

Harris角点检测算法是通过微分运算和自相关矩阵来检测角点的，其中微分运算能够反映像素点在任意方向灰度的变化量[27]，因而能够有效地区分出角点和边缘点。设像素点(,)的灰度值为(,)。若以像素点(,)为中心的小窗口，在,方向上分别移动微小的位移,，则灰度(,)变化的表达式为

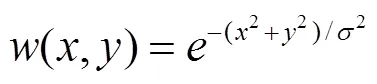
()的矩阵形式为

由以上各式得出(,)的性质主要由自相关矩阵决定，由于自相关矩阵的特征值不易计算，通常选择计算每个像素点的角点响应函数CRF

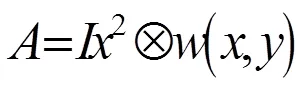
系数为Harris算法的经验常数，一般为0.04～0.06。以每个像素点为中心取其3×3的邻域，若中心像素点的角点响应函数值大于某个设定的阈值并且是该邻域的最大值，则该像素点可判定为角点[28]。

2 改进的自适应Harris角点检测算法

2.1 改进算法的思想

Harris角点检测算法是一种经典的角点检测算法，虽然具有旋转和仿射变换不变性，但在实际应用中仍存在一些不足：1）Harris算法在提取角点时，需要在设定阈值的基础上进行非极大值抑制，而且阈值的设置决定了角点提取的准确度，阈值设定偏大则会引起角点的丢失，偏小则会导致提取大量伪角点；2）Harris算法中的角点响应函数中的系数需要随图像的变化进行人为调整，智能化程度低，使其在实际应用中效率降低。针对上述问题，本文提出一种基于图像像素自相关矩阵的改进的Harris角点检测算法：首先，对图像做方向滤波，再进行高斯平滑，减少噪声点的干扰；然后计算图像像素的自相关矩阵行列式，以此构造特征角点图像；最后对特征角点图像进行OTSU阈值分割筛选出预选区域，结合改进的非极大值抑制方法提取邻域最佳角点。该算法舍弃了经典Harris算法中的角点响应函数和非极大值抑制阈值2个参数，直接从与图像角点检测真正相关的像素自相关矩阵入手，避免了Harris算法需要设定2个阈值的随机性和不确定性等缺点。无需人为调整阈值大小，通过OTSU计算得出自适应阈值，以期提高工作效率和角点检测精度，突出体现角点检测智能化的特点。具体改进算法的流程图如图1所示。

图1 基于像素自相关矩阵的角点检测算法流程图

2.2 改进算法的实现步骤

由于Harris角点检测响应函数CRF受系数影响，所以角点提取的效果依赖于系数的设定，因此对于某一幅图像可能需要多次人工交互调整系数才能获得理想的检测结果。考虑到人为设定系数的随机性，本文对经典的Harris角点检测算法进行了改进，通过计算图像像素的自相关矩阵行列式来构造特征角点图像，在此基础上通过OTSU算法计算特征角点图像的自适应分割阈值来筛选出角点预选区域，最后采用改进的非极大值抑制方法来判定邻域最佳角点，这样避免了人为设定所造成的误差，提高了检测效率与精确度。

2.2.1 计算像素自相关矩阵构造特征角点图像

计算灰度图像上像素点(,)在水平方向与垂直方向上的梯度、及其乘积，通过高斯平滑函数(,)对其进行滤波计算，得出图像像素的自相关矩阵，在此应该注意掌握高斯平滑窗口的尺寸，以不超过7×7为宜。若窗口选择偏大在卷积运算过程中会导致角点位置的偏移；若窗口选择偏小会由于噪声点的影响呈现出较多的伪角点。计算图像每个像素自相关矩阵的行列式，在此基础上构造特征角点图像。

2.2.2 对特征角点图像进行OTSU阈值分割

1类和2类以及整幅图像的灰度均值1，2，T分别为

1类和2类的方差分别为

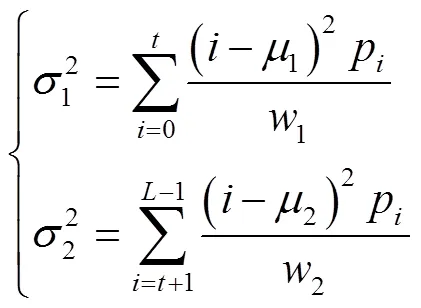
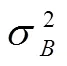
以此对特征角点图像进行阈值分割，筛选出预选区域。

2.2.3 使用非极大值抑制方法提取最佳角点

为了提高检测效率以及准确性，本文根据Neubeck[30]等改变模板窗口大小以及分块处理的方法，采用改进的非极大值抑制算法对图像预选区域进行阈值分割并提取角点，具体算法步骤如下。

首先，计算图像像素自相关矩阵行列式得出图像的梯度变化剧烈区域，将这些预选区域划分成多个尺寸为(+1)×(+1) 像素的正方形子区，如图2所示；其次，设定一个窗口为3×3像素的正方形模板，在该子区中对应的每个正方形模板搜索梯度为极大值的候选点，图2中的黑点表示该子区中筛选出的候选点集；最后，对该子区中的候选点集结合自适应阈值做完整邻域的角点检测。依照上述方法对整体预选区域执行非极大值抑制，剔除边缘上的伪角点，从中检测出图像的最佳角点。该方法可以减少运算量，快速精准地检测出角点。

图2 改进的非极大值抑制方法示意图

3 试验与结果分析

3.1 试验方法

为了验证本算法角点检测的性能，选择角点特征比较明显的5幅图像，包括经典的立方体图像，某高校宿舍楼图像，某大厦图像，以及高分二号遥感图像作为数据源，采用经典的Harris算法和本文提出的改进算法进行仿真试验，并对检测结果进行数据对比分析。试验环境为Inter(R) Core(TM)2处理器、2GB内存、64位Window7操作系统、Matlab R2014b

3.2 试验结果

角点检测试验结果如图3～图7所示。图3－图7分别为针对立方体、高校宿舍楼、建筑大厦图像及高分二号遥感影像进行的角点提取的对比试验结果。

图3 立方体图像角点检测算法结果对比

图4是采用高校宿舍楼图像进行角点提取的对比试验结果，其中图4a为原图，图4b为对原图进行自相关行列式计算得出的特征角点图像，图4c为采用经典的Harris算法和本文改进算法提取的角点差异图，图4d为局部差异图。图4c和图4d中红色十字为Harris算法提取结果，绿色圆圈为本文算法提取结果。

注：图c, d中红色十字为Harris算法提取结果，绿色圆圈为本文算法提取结果。下同。

图5 Harris与本文算法高层建筑物图像角点检测结果对比

除了通用的图像格式数据外，针对角点检测是遥感图像配准和镶嵌自动化的关键步骤，本文进行了针对高分二号遥感影像的2组试验（图6，图7）。其中图6为高分二号遥感影像GF2_PMS2_E116.7_N40.0_20160609_L1A0001633143北京首都国际机场的部分图像开展角点检测试验。图7是应用高分二号遥感影像GF2_PMS1_E82.7_N44.7_20160626_L1A0001666662中农作物植被的部分影像进行的角点提取的对比试验结果。

图6 Harris与本文算法高分二号遥感融合影像角点检测结果对比

图7 农作物植被部分遥感影像Harris算法与本文算法角点检测结果对比

从以上2种算法的角点检测结果差异图中可以直观看出本算法角点检测结果优于经典Harris算法，具体数据见表1和表2列出。其中表1包含图像不同算法的重要参数，表2中的标志点数表示标记出的角点数，正确数表示检测出的真正角点数，漏检数表示未被检测出的角点数，误检数表示检测出的伪角点数，准确率为检测出的角点数与图像总角点数之比。

表1 所有附图参数一览表

表2 角点检测统计

从以上对比试验结果以及表格分析可得出，图3为简易的立体几何图形，其Harris算法的准确率比改进算法低30.51个百分点，图4和图5为建筑物图像，其Harris算法的准确率比改进算法分别低13.36个百分点和3.07个百分点，图6和图7为高分二号遥感影像，其Harris算法的准确率比改进算法分别低7.55个百分点和27.06个百分点，对于不同类型的图像，改进算法的准确率均有提升。Harris算法容易误提取出边缘上的伪角点，角点提取的准确率不高，并且角点定位存在偏差。这些缺点取决于Harris算法采用了较为单一固定的系数和非极大值抑制系数的阈值，使该算法只能针对某些特定图像提取较好的结果，而在实际应用中，并不适应其他图像。若要改善提取效果，则需反复试验更改2个阈值，增大工作量降低运算效率。本算法避免了阈值的反复设定，应用OTSU算法直接从特征角点图像中计算出分割阈值，从而筛选出预选区域，最后通过改进的非极大值抑制方法检测出最佳角点。改进的算法具有较好的智能性，避免了设定Harris算法中角点响应函数系数阈值与大抑制系数阈值的随机性和主观性，能够获得更多的有效角点，减少了伪角点的提取，并且具有较高的定位精度。从图4d、图5d、图6d中可以明显看出，本论文算法较传统算法能够更准确地定位角点。图3d中的六棱柱最上面的2个角点均未能检出，主要原因是图像已经过拉伸处理，原图中这两个角点的灰度值很低，在单阈值情况下较难检测出来，可以考虑分窗口检测，每个窗口单独计算阈值，这样提取效果会更好些。图5c和图6c的Harris算法角点提取总数虽然比本文算法的角点提取总数多，但是很多角点都是位于图像的边缘轮廓，并非图像中有价值的角点，相比而言，本文算法所提取出的角点更有实际价值。

4 结 论

本文针对经典Harris角点检测算法中角点响应函数的系数和阈值的随机性以及需要设定非极大值抑制系数阈值等方面的不足，提出采用自相关矩阵和自适应阈值相结合的改进算法。应用自相关矩阵对图像进行处理，提取特征角点图像，在此基础上应用OTSU分割算法得到自适应阈值，避免了人为设定阈值的随机性和反复性，并提出改进的非极大值抑制方法。与经典的Harris算法相比较，本算法有如下几个优势：1）通过直接计算图像像素的自相关矩阵行列式来构造特征角点图像，改进优化了角点检测模型；2）可以不依赖于人为设定参数，提高了角点检测的智能性和时效性；3）能够较准确地定位角点并剔除伪角点，具有更好的检测性能，针对农作物植被遥感图像角点检测的准确率校经典Harris算法提高27.06个百分点；4）能够针对多种图像格式进行角点检测，具有更强的适应性。如何更为客观地评价角点检测结果，构造更为有效的角点检测分析模型，拓展其在农业信息化领域的作用，也是值得进一步研究的方向。

[1] Chen Jie, Zou Lihui, Zhang Juan, et al. The comparison and application of corner detection algorithms[J]. Journal of Multimedia, 2009, 4(6): 435－441.

[2] Paul J, Oechslein B, Erhardt C, et al. Self-adaptive corner detection on MPSoC through resource-aware programming original[J]. Journal of Systems Architecture the Euromicro Journal, 2015, 61(10): 520－530.

[3] 姚国标，邓喀中，张力，等. 基于 Harris-Affine 的宽基线立体影像LSM匹配方法[J]. 中南大学学报，2014，45(8)：2661－2668.

Yao Guobiao, Deng Kazhong, Zhang Li, et al. Least square matching method for wide baseline stereo images based on Harris-Affine features[J]. Journal of Central South University, 2014, 45(8): 2661－2668. (in Chinese with English abstract)

[4] Mokhtarian F, Mohanna F. Performance evaluation of corner detectors using consistency and accuracy measures[J]. Computer Vision and Image Understanding, 2006, 102(1): 81－94.

[5] 邢远秀，章登义，赵俭辉. 利用多尺度弦角尖锐度累积的自适应角点检测算子[J]. 武汉大学学报信息科学版，2015，40(5)：617－627.

Xing Yuanxiu, Zhang Dengyi, Zhao Jianhui. An adaptive threshold corner detector based on multi-scale chord-angle sharpness accumulation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 617－627. (in Chinese with English abstract)

[6] Chen Suting, Meng Hao, Zhang Chuang, et al. A KD curvature based corner detector[J]. Neurocomputing, 2016, 172(2): 434－441.

[7] Smith S M, Bpady J M. SUSAN-A new approach to low level image processing[J]. International Journal of Computer Vision, 1997, 23(1): 45－47.

[8] Harris C G, Stephes M J. A combined corner and edge detector[C]//Proceeding of Fourth Alvey Vision Conference, 1988: 147－151.

[9] Cordelia Schmid, Rrger Mohr. Christian bauckhage evaluation of interest point detectors[J]. International Journal of Computer Vision, 2000, 37(2): 151－172.

[10] Moravec H P. Towards automatic visual obstacle avoidance[C]//Proceedings of the 5th International Joint Conference on Artificial Intelligence, 1977: 584－590.

[11] 赵斌，周军. 基于改进棋盘的角点自动检测与排序[J]. 光学精密工程，2015，23(1)：237－244.

Zhao Bin, Zhou Jun. Automatic detection and sorting of corners by improved chessboard pattern[J]. Opt. precision Eng, 2015, 23(1): 237－244. (in Chinese with English abstract)

[12] Zhang W C, Shui P L. Contour-based corner detection via angle difference of principal directions of anisotropic Gaussian directional derivatives[J]. Pattern Recognition, 2015, 48(9): 2785－2797.

[13] 陈华伟，吴禄慎，袁小翠. 基于链码改进算法的钢轨表面缺陷识别[J]. 计算机工程与设计，2015，36(11)：3097－3101. Chen Haiwei, Wu Lushen, Yuan Xiaocui. Rail surface defect detection based on improved chain-code algorithm[J]. Computer Engineering and Design, 2015, 36(11): 3097－3101. (in Chinese with English abstract)

[14] 李振华，江耿红，徐胜男，等. 基于轮廓多边形拟合的红外与可见光图像配准算法[J]. 系统工程与电子技术，2015，37(12)：2872－2878.

Li Zhenhua, Jiang Genghong, Xu Shengnan, et al. Image registration algorithm for infrared and visible images based on contour polygon fitting[J]. Systems Engineering and Electronics, 2015, 37(12): 2872－2878. (in Chinese with English abstract)

[15] Mokhtarian F, Bober M. Robust image corner detection through curvature scale space[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1988, 6(1): 121－128.

[16] 侯北平，李平，宋执环. 纸浆纤维的形状特征提取应用研究[J]. 浙江大学学报：工学版，2006，40(7)：1132－1136.

Hou Beiping, Li Ping, Song Zhihuan. Applied study on paper fibre shape characteristics extraction[J]. Journal of Zhejiang University: Engineering Science, 2006, 40(7): 1132－1136. (in Chinese with English abstract)

[17] 赵萌，温佩芝，邓星，等. 一种参数自适应的Harris角点检测算法[J]. 桂林电子科技大学学报，2016，36(3)：215－219. Zhao Meng, Wen Peizhi, Deng Xing, et al. A parameter adaptive Harris corner detection algorithm[J]. Journal of Guilin University of Electronic Technology, 2016, 36(3): 215－219. (in Chinese with English abstract)

[18] Mikolajczyk K, Schmid C. Scale and affine invariant interest point detector[J]. International Journal of Computer Vision, 2004, 60(1): 63－86.

[19] 王玉珠，杨丹，张小洪. 基于B样条的改进型Harris角点检测算法[J]. 计算机应用研究，2007(2)：192－194.

Wang Yuzhu, Yang Dan, Zhang Xiaohong. Improved harris corner detection algorithm based on B-spline[J]. Application Research of Computers, 2007(2): 192－194. (in Chinese with English abstract)

[20] Gevrekci M, Gunturk B K. Reliable interest point detection under large illumination variations[C]//IEEE International conference on Image Processing, ICIP, 2008: 869－872.

[21] 龙中杰，王吉芳，左云波. 一种改进的Harris与Susan相结合的角点检测方法[J]. 计算机应用与软件，2013，30(12)：133－136.

Long Zhongjie, Wang Jifang, Zuo Yunbo. An improved corner detection algorithm with the combination of harris and susan[J]. Computer Applications and Software, 2013, 30(12): 133－136. (in Chinese with English abstract)

[22] 毛雁明，兰美辉，王运琼，等. 一种改进的基于Harris的角点检测方法[J]. 计算机技术与发展，2009，19(5)：130－133.

Mao Yanming, Lan Meihui, Wang Yunqiong,et al. An improved corner detection method based on harris[J]. Computer Technology and Development, 2009, 19(5): 130－133. (in Chinese with English abstract)

[23] 李海，张宪民，陈忠. 基于直线检测的棋盘格角点自动提取[J]. 光学精密工程，2015，23(12)：3480－3489.

Li Hai, Zhang Xianming, Chen Zhong. Automatic corner detection of checkerboard based on LSD[J]. Opt.precision Eng2015, 23(12): 3480－3489. (in Chinese with English abstract)

[24] Mokhtarian F, Suomela R. Enhancing the curvature scale space corner detector[C]//Proc. of Scandinavian Conf. Image Analysis. Bergen, Norway: Int. Assoc. Pattern Recognition, 2001: 145－152.

[25] Awrangjeb M, Lu G J. Robust image corner detection based on the chord-to-point distance accumulation technique[J]. IEEE Transactions on Multimedia, 2008, 10(6): 1059－1072.

[26] 周志艳，闫梦璐，陈盛德，等. Harris 角点自适应检测的水稻低空遥感图像配准与拼接算法[J]. 农业工程学报，2015，31(14)：186－193.

Zhou Zhiyan, Yan Menglu, Chen Shengde, et al. Image registration and stitching algorithm of rice low-altitude remote sensing based on Harris corner self-adaptive detection[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(14): 186－193. (in Chinese with English abstract)

[27] 邓淇元，曲长文，江源. 基于圆环模板的改进Harris角点检测算法[J]. 系统工程与电子技术，2016，38(4)：949－954. Deng Qiyuan, Qu Changwen, Jiang Yuan. Improved corner detection algorithm based on circle mask via harris[J]. Systems Engineering and Electronics, 2016, 38(4): 949－954. (in Chinese with English abstract)

[28] 吴鹏，徐洪玲，李雯霖，等. 基于区域检测的多尺度Harris角点检测算法点检测[J]. 哈尔滨工程大学学报，2016，37(7)：969－973.

Wu Peng, Xu Hongling, Li Wenlin, et al. Multi-scale Harris- corner detection algorithm based on region detection[J]. Journal of Harbin Engineering University, 2016, 37(7): 969－973. (in Chinese with English abstract)

[29] Otsu N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man and Cybernetics, 1979, 9(1): 62－66.

[30] Neubeck A, van Gool L. Efficient non-maximum suppression[C]//Proceedings of the 18th International Conference on Pattern Recognition, 2006, 3: 850－855.

An adaptive threshold corner detection algorithm based on auto-correlation matrix of image pixel

Deng Xiaolian1, Du Yuqi1, Wang Changyao2, Wang Xiaohua1

(1443002,;2100101,)

Harris algorithm is a classical corner detection algorithm. It can extract corners of image quickly and has a certain degree of anti-noise ability, but it has corner location error to some extent. It needs to artificially set 2 threshold parameters, and it can not easily eliminate false corners such as edge points, so it has somewhat lower accuracy of corner detection. For above-mentioned reasons, a modified Harris corner detection algorithm based on auto-correlation matrix of image pixel was proposed in this paper, and the purpose was not only to solve the problem of the variability and randomness of setting thresholds for corner response function (CRF) and non-maximum suppression in Harris algorithm, but also to improve the accuracy of corner location. In our paper, the most important innovation is embodied in 2 aspects: One is avoiding to set 2 thresholds of traditional Harris corner detection algorithm artificially, the other is locating corner more accurately by modified non-maximum suppression method. Firstly, original image was filtered by directional filtering and Gaussian low-pass filtering, and feature corner image was constructed by calculating determinant of every pixel’s auto-correlation matrix. Potential corners of image could be heightened effectively, which had more significant intensity than other surrounding pixels, and could be recognized easily in feature corner image. Secondly, in order to improve intelligent level of the modified algorithm, we selected adaptive OTSU algorithm to determine segmentation threshold. The segmentation threshold of feature corner image could be calculated by OTSU algorithm, and the pre-selected regions were obtained. So the search range of corner detection was significantly decreased. On the basis, an optimized non-maximum suppression method was adopted in our research, which could divide each pre-selected region into several 3×3 square subranges, and correct corners were extracted from potential corners of each square subrange, false corners were eliminated effectively. Finally, in order to validate the efficiency and reliability of the modified algorithm, 5 groups of comparison experiments were performed in our research. Five images, including generic image format (jpg, bmp), and multi-band remote sensing image format (GF-2 data), were selected to test performance of the modified algorithm and Harris algorithm, which contained the total of detection corners, the number of correct corners, the number of false corners, the number of omissive corners, and the detection rate of correct corners. According 5 groups of comparison experiments, the accuracy of corner detection in different types of images is improved, for crop vegetation remote sensing image, the accuracy of corner detection is improved by 27.06 percentage points. We can draw a conclusion that the improved algorithm can not only calculate the optimal threshold automatically, but also locate the corners more accurately. Therefore, our modified algorithm can greatly improve the precision of corner detection. The proposed algorithm is more accurate and efficient than traditional algorithm, its adaptive characteristic makes it easy to be integrated in an image processing system or image registration module, and it has higher feasibility and application value. Experiments also show that there is some insufficiency to be improved in our research, for example, some corners in picture of cubes could not be detected correctly with either our modified algorithm or Harris algorithm. In our future research, we propose to partition an image into several sub-image blocks, and independently determine each sub-image block’s segmentation threshold by OTSU algorithm, so that the corners not prominent in full image can be significantly strengthened in sub-image blocks, and can be detected correctly. The research could provide reference for agricultural remote sensing image data detection.

image processing; algorithms; corner detection; auto-correlation matrix; feature corner image; non-maximum suppression

10.11975/j.issn.1002-6819.2017.18.018

TP391.41

A

1002-6819(2017)-18-0134-07

2017-03-09

2017-08-11

遥感科学国家重点实验室课题(Y6Y00200KZ)

邓小炼，男，重庆人，博士，副教授，主要从事遥感信息处理，模式识别，变化检测等方面的研究。Email：345937408@qq.com