振动激励下枣树力传递效果室内模拟试验

付 威，张志元，刘玉冬，潘俊兵，崔 健，丁 凯，张慧明



振动激励下枣树力传递效果室内模拟试验

付 威，张志元，刘玉冬，潘俊兵，崔 健，丁 凯，张慧明※

（石河子大学机械电气工程学院，石河子 832003）

为了提高林果振动采收的作业效率，根据果品在振动过程中瞬时加速度的变化，研究其振动采收时力的传递效果，降低激振功耗。该文以红枣振动采收为研究对象，建立红枣“枝-柄-果”的双摆振动模型，分析系统振动过程中的固有频率，获得系统的固有振动频率为14.69、17.26 Hz；利用振动试验测试系统，进行扫频试验，测得枣树发生共振频率的范围集中出现在12～24 Hz；当振幅分别为3、5、7 mm时，频率在12～24 Hz时进行枣树的定频振动试验，通过DHDAS分析软件分析，获得枣树的振动频率和瞬时加速度的关系；对受迫振动的红枣采用3D高速摄像技术进行运动分析，获得红枣在空间的最大瞬时加速度值，通过统计计算分析，红枣的最大瞬时惯性力值均大于果柄最大拉断力6 N。试验表明在振幅为7 mm、频率为17 Hz时，红枣振动采收过程中，力的传递效果较好。该研究可为红枣收获机激振系统的设计提供理论依据和技术参考。

振动；力学性能；试验；红枣；激振频率

0 引 言

新疆以其独特的地理位置和气候条件，非常适宜栽植品质优良的红枣[1-2]。据统计，截止2015年底，新疆红枣栽植面积已突破52万hm2，跃居全国首位。目前，新疆枣树已到盛果期，红枣采收完全依靠人工，作业效率低，成本高，已成为新疆红枣产业持续发展的瓶颈[3]。因此，亟需采用机械化作业，提高红枣采收效率，降低人工成本[4]。红枣的机械化采收主要采用振动方式将树上红枣振落。振动过程中，收获机械以一定振幅和频率击打枣树的主干或侧枝，从激振部位开始产生振动，并沿主干将激振力传递给侧枝和枣吊，最后传递到红枣，在空间上红枣将产生多维激励，当红枣惯性力大于与枣-柄连接力时，红枣完成掉落，实现振动采收。

为提高果品采收效率，降低果树损伤，减少能量损耗，国内外已对果品收获的振动参数与采收效果进行相关研究。Logavi等[5]对柑橘果实采摘的最优频率和幅值进行了深入研究；Mateev等[6]建立了酸樱桃在不同振动条件下采净率的概率统计模型；Castro-García等[7]从形态学角度建立了橄榄树受迫振动的动力学模型；He Long等[8]研究单一树枝的能量传递，分析振动频率对落果率的影响；Upadhyyaya等[9]用单摆模型对果-柄系统进行了振动模态分析；Rand等[10]通过双摆模型对“枝-果-柄”间的耦合振动关系进行了研究，Cooke等[11-12]通过对双摆模型添加阻尼等约束条件，进一步对该模型进行优化。Du等[13-17]对甜樱桃及山核桃机械振动式采机理进行了初步探究，从树木形态学对能量传递的影响进行了试验研究；瞿维等[18-20]对杏果实振动采收速度规律等进行了试验研究；王长勤等[21]对核桃树在不同激振频率下果实的采净率进行了试验研究；王业成等[22-23]对黑加仑在不同振动频率、振幅、激振位置的采收率进行了试验研究；刘继展等[24]建立了一种面向穗轴激励输入的果穗振动仿真模型，并对模型进行了仿真分析。

通过上述研究可知，针对红枣振动采收的力传递效果研究未见报道。本文以红枣为研究对象，研究振动频率和振幅对枣树力传递效果的影响，并进行红枣力传递效果的振动试验，为红枣收获机整机的激振系统设计提供理论依据和技术支持。

1 试验台的组成及工作原理

1.1 试验台的组成

试验设备主要有DC-300-3/SV-0505电动振动试验系统（苏州苏试试验仪器有限公司研制），该电动振动系统主要由DC-300-3电动振动台台体、SV-0505水平滑台、自制夹具、功率放大器SA-3、RC-2000振动控制器、YMC92系列动态数据采集器、压电式加速度传感器DH311E 、DHDAS 软件及电脑及相关处理软件等组成。试验台的组成如图1所示。

1.冷却出风口 2.DC-300-3电动振动台台体 3.联接器 4.滑台台面 5.可调夹具 6.滑台支座 7.水平滑台 8.底座 9.电脑 10.YMC92系列动态数据采集器 11.信号放大器 12.RC-2000振动控制器 13.功率放大器

1.2 试验台的工作原理

电动振动试验台利用了“弗莱明左手法则”，通有交变电流的线圈在恒定磁场中会产生交变的直线运动。如图1所示的振动台体内安装有励磁线圈，直流电经由功率放大器供给其恒定的励磁电流，产生稳恒磁场。工作时，RC-2000振动控制系统发出的指令产生一定频率的正弦交流信号并通过功率放大器后驱动振动台体2内的驱动线圈，振动台体内的动圈将产生交变直线运动，经由联接器3传递给滑台台面4，固定在夹具5上的树体便同滑台一起运动。同时，固定在树体上加速度传感器会将树体运动产生的加速度信号传输给动态数据采集器11，实时测得的数据在DHDAS分析软件中存储。

2 力的传递效果理论分析

为了研究红枣树受迫振动的力传递效果，首先建立红枣的力传递模型，分析其频率、振幅和采收效果的关系。可将红枣的“枝—柄—果”近似地看作一个动态模型，可以简化成振动模型中的双摆[25-28]。简化后的模型，如图2所示，以枣柄与果枝结点为原点，建立如图所示坐标系，将枣柄与果枝、枣柄与红枣简化为两个结点，设定弹性系数为，黏性阻尼系数为；果柄、红枣的质量分别为、，g；枣柄长为，mm；为便于计算，将红枣视为半径为的椭圆球，mm；、分别为椭圆球的半长轴与半短轴，mm；为果柄在轴方向的偏转角，rad；为红枣在轴方向内的偏转角，rad；为红枣在轴方向内的偏转角，rad。根据拉格朗日方程

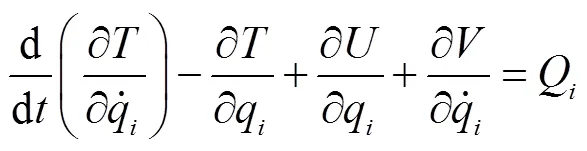
式中为动能，J；为势能，J；为瑞利耗散函数；q为广义坐标；Q为外力，N。

注：是以枣柄外端为原点建立的坐标系，是以枣的几何中心为原点建立的坐标系；为枣柄在轴方向的偏转角，rad；为红枣在轴方向内的偏转角，rad；为红枣在轴方向内的偏转角，rad；为点与枣柄质心间距，mm；为枣柄长度，mm；为红枣半长轴，mm；为红枣半短轴，mm；为椭圆球的半径，mm；为枣柄的质量，g；为红枣的质量，g；1、2、3为弹性系数；1、2、3为黏性阻尼系数。

Note:is coordinate system based on the outer end of the jujube stem,is coordinate system based on the jujube’s center；is the deflection angle of jujube stem in the-axis direction, rad;is the deflection angle of jujube in the-axis direction, rad;is the deflection angle of jujube in the-axis direction, rad;is the distance between thepoint and the center of the jujube stem, mm;is the length of jujube stem, mm;is the half-long axis of jujube, mm;is the semi-short axis of jujube, mm;is the ellipsoid radius, mm;is the mass of jujube, g;is the mass of jujube, g;1,2,3is coefficient of elasticity;1,2,3is viscous damping coefficient.

图2 “果-柄-枝”双摆模型

Fig.2 Double pendulum model of “fruit- handle –branch”

枣柄与红枣的动能

枣柄与红枣的势能

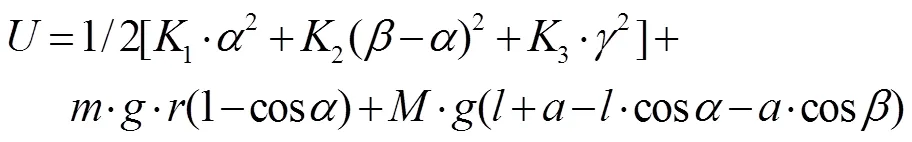
瑞利耗散函数

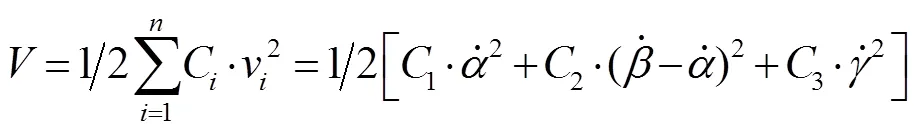
其中J为果柄重心关于点的转动惯量，kg·m2；J为红枣关于轴的转动惯量，kg·m2；J为红枣关于轴的转动惯量，kg·m2；C为黏性阻尼系数；V为角加速度，rad/s2；=1, 2, 3。

由于振动过程中，主要是振幅和频率的变化[29]，的角度变化非常小，所以与之差趋于零，即

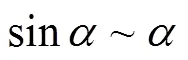
忽略黏性阻尼系数和弹性系数，联立（2）、（3）、（4）代入（1）式化简可得

式中、为动态模型所受外力，N。

将（5）、（6）式写成矩阵形式

其中{}为外力矩阵，即有

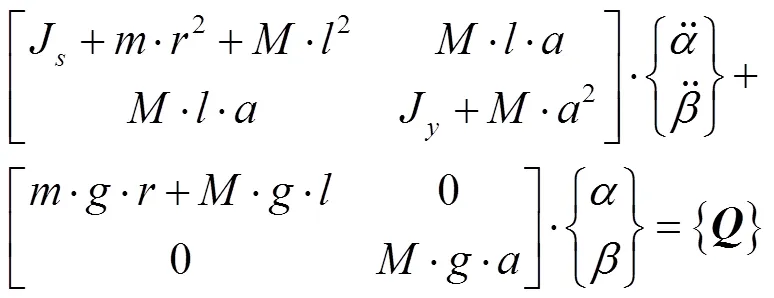
当外力为零时，（7）式可化简为

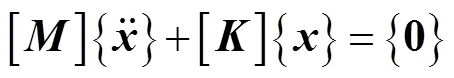
设上式的解x具有以下形式

式中A为常数；为角频率，rad/s；为相位角，rad。

则（8）式的特征方程为

化简得

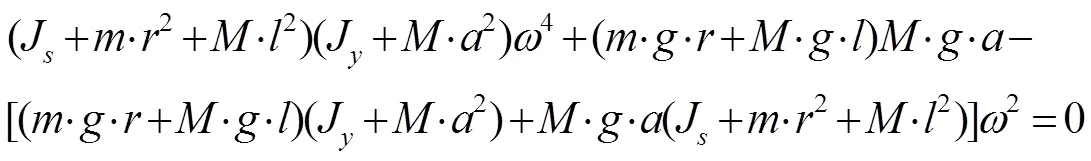
则频率为：

本次试验以骏枣为研究对象，共进行5次测试，每次测试30个骏枣，通过试验测得：枣柄质量为（0.08±0.02） g；骏枣质量为（13±5） g；骏枣半长轴为（27.5±2.5 ）mm；枣柄长度为（3.75±0.95 ）mm；骏枣半短轴为（11.5±4.5） mm。将上述数值中最大值和最小值分别代入（11）、（12）式，可得系统的固有振动频率分别为=14.69、17.26 Hz。

3 振动扫频试验

为获得不同果枝的共振频率，首先对选取的样本树进行了扫频试验，分析扫频试验结果，获得不同果枝发生共振时的激振频率与振幅。

3.1 样本树的结构

选取5年生俊枣树（新疆生产建设兵团第一师十一团五连红枣高效栽培示范园）为试验样本。试验前先去掉枣树根部，枣树主干高1为0.4 m，树冠高度2为2 m，树冠最大直径为1.5 m，根据果树形态学，样本树被划分为主干、主枝、二次枝及枣吊部分，根据树形结构，建立枣树4个力的传递路径Ⅰ、Ⅱ、Ⅲ、Ⅳ，如图3所示。

3.2 试验过程及分析

试验时，将样本树主干的下端0.2 m处通过自制夹具竖直固定在振动试验台上。3个传感器沿滑台振动方向水平分别固定于对应路径（Ⅰ、Ⅱ、Ⅲ、Ⅳ）的主枝上，其中编号为1的传感器距离夹持点0.3 m处，编号为2、3的传感器分别沿间隔距离为0.15 m顺序固定，根据相应路径进行扫频试验，如图3所示。

注：h1为枣树主干高，h2为树冠高度，D为树冠最大直径，Ⅰ、Ⅱ、Ⅲ、Ⅳ为不同路径。

根据前期预试验以及振动试验台所承载能力，将振动控制器频率参数设置在0～24 Hz内，振幅分别设为3、5、7 mm进行振动扫频试验，获得各测试点的共振频率。如图4所示为时域频域图，其中图4a是在扫频过程中压电式传感器的电压值与时间变化；图4b是在时域内选中区域的测试点的瞬时加速度与时间变化；图4c是在频域内选中部分共振出现时，测试点的频率值与时间对应关系，图中不同颜色的曲线表示各测试点振幅随频率的变化。在0～280.0 s测试时间内，3个测试点共振发生的时间都集中在200.0～253 s，在共振时域内又可以分为4个时间段，即第1段时间204～213.5 s、第2段时间213.5～222.5 s、第3段时间225.5～235.5 s、第4段时间245.5～252.5 s。从频域图中可知，靠近激振源（滑台）的加速度传感器（编号为1的传感器）先达到最大幅值（mV），此时共振频率较小；随着扫频的频率增加，其余2个测试点的瞬时加速度幅值也先后达到最大幅值（mV），对应的共振频率增大。根据每个路径扫频结果可知，共振的发生，随着与激振源的距离逐渐增大，振动频率也逐渐增大，每个路径中的3个测试点获得共振频率为12～24 Hz。

4 振动效果试验

4.1 定频振动试验

4.1.1 试验方法

为研究振动频率和振幅对样本树各枝干瞬时加速度的影响，进行了定频振动试验。根据扫频试验结果，在12～24 Hz频域内进行定频振动试验。振动频率分别为12、13、14、……、24 Hz共13个振动频率，振幅分别为3、5、7 mm，测试路径为4个路径。试验总次数为

定频试验时，共布置6个压电式加速度传感器，其中加速度传感器1布置在主干上，其余5个加速度传感器2-6沿每个路径按编号由低到高布置，各传感器间距为150 mm（由于振动能量沿路径传递过程中枝干分叉点处能量损失最大，因此传感器避开分叉点）。

注：图a是加速度传感器电压值随时间变化；图b为图a电压值与传感器对应灵敏度的比值（截取其中一段共振区域）；图c为共振点（3、5、7 mm振幅时）的振幅与频率变化关系；Input0-1 A为编号为1的传感器；Input0-2 A为编号为2的传感器；Input0-3 A为编号为3的传感器。

Note: Fig.a is the changes on voltage of acceleration sensor with time; Fig.b is Fig.the ratio of voltage value to sensitivity of the sensor (intercepting one of the resonance area); Fig.c is the relationship between the amplitude and frequency of the resonance point (3,5,7 mm amplitude); Input0-1 A is the number 1 sensor; Input0-2 A is the number 2 of the sensor; Input0-3 A is the number 3 of the sensor.

图4 振动扫频图谱

Fig.4 Vibrational sweep pattern

4.1.2 结果分析

如图5所示，定频试验获得不同路径（Ⅰ、Ⅱ、Ⅲ、Ⅳ）的瞬时加速度与激振频率关系图。定频测试范围12～24 Hz，瞬时加速度的值主要分布在3～40 m/s2。路径I：当振幅分别为3、5、7 mm时，3456第一次出现共振时的频率分布在14～16 Hz，56的加速度幅值变化较大；路径II：当振幅分别为3、5、7 mm时，2、3、4、5、6第一次出现共振时的频率分布在14～15 Hz，456的加速度幅值变化较大；路径II：当振幅分别为3、5、7 mm时，123456第一次出现共振时的频率分布在13～16 Hz，3456的加速度幅值变化较大；路径IV：当振幅分别为3、5、7 mm时，56第一次出现共振时的频率分布在14～15 Hz，56的加速度幅值变化较大；第二次出现共振时的频率分布在16～18 Hz，其中56在测试区间内的加速度出现最大值。利用Design-expert对加速度与频率进行相关性分析，如表1所示。瞬时加速度123的有正相关性，相关系数值均大于0.6，而瞬时加速度456的正相关性随着测试点距离振源越远，正相关性越不明显。通过分析可知，距离激振源越远，发生共振时的瞬时加速度变化就越大，瞬时加速度值随振幅的增加变化不明显；枣树的分叉点和直径对共振幅值的变化影响较大[30]，且路径的分叉点越多，瞬时加速度变化越小。

4.2 力的传递效果试验

4.2.1 试验方法

为观察振动试验效果，研究定频试验时共振所发生的各枝干瞬时加速度与果实振动效果的关系。随机选取4颗骏枣，并编号枣1、枣2、枣3、枣4，将对应的红枣质量进行3次称量并计算平均值，枣1的质量(16.159±0.002) g，枣2的质量(10.593±0.001) g，枣3的质量(17.596±0.003 )g，枣4的质量(12.376±0.003) g。选取弹性和刚度与枣柄相似的胶线作为枣柄，将红枣布置在样本树各路径的不同位置，模拟红枣的“枝－柄－果”挂接形式。通过3D高速摄像机（FASTECIMAGING-TS4，最大分辨率为1 280×1 024 dpi，在最大分辨率时每秒500帧）对红枣的空间运动轨迹进行拍摄，观察红枣在激振器的作用下产生多维激励。用3D ProAnalyst分析软件对红枣的空间运动进行后处理，获得红枣的在空间的最大瞬时加速度值。

图5 样本树测试点加速度图

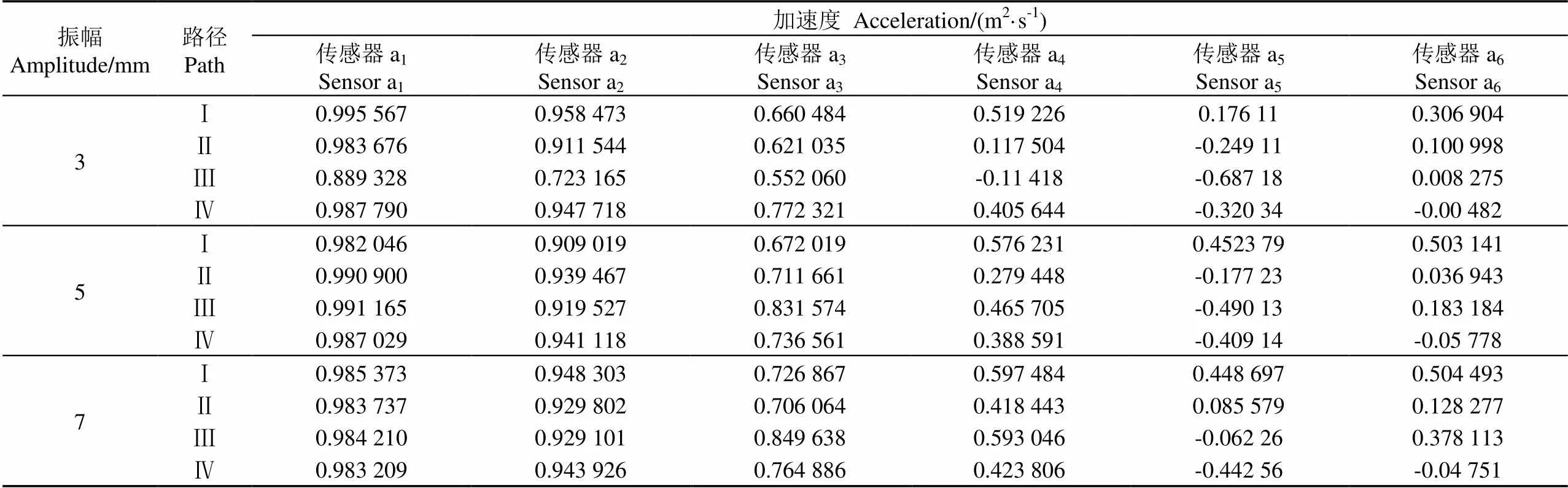
表1 振幅和加速度的相关系数

试验时，首先利用3D坐标板对样本树进行标定，如图3所示。根据红枣在树枝上的不同结果位置，将红枣依次地布置在样本树上。按定频试验顺序安排4个路径的试验,每个路径4个红枣，具体试验步骤与定频试验相同，共156组试验。

4.2.2 结果分析

通过3D ProAnalyst分析软件对定频试验中3D高速摄像机所拍摄的红枣在空间运动的轨迹进行分析。由于试验数据数量较大，在利用ProAnalyst分析软件进行试验分析时，选取在振动过程中振动变化较为平稳的一段（约500帧）作为此次的试验数据采集样本，通过统计分析，找出每个红枣在该段的最大瞬时加速度及最小瞬时加速度，并计算出每个红枣瞬时速度（共13个）的平均值和变异系数，如表2所示，分别是振幅为3、5、7 mm时4颗试验红枣的瞬时加速度。根据台架试验红枣果柄的最大拉断力为6 N[31]，由=（其中为红枣的质量；为红枣的加速度）可计算出该试验过程中，红枣受到激励产生的惯性力。根据测试4个路径中挂接的红枣产生的瞬间惯性力值，均大于6 N，可知红枣均能够从枣树上振落。

通过表2分析可知：当振幅越大时，红枣的最大瞬时加速度整体呈逐渐增大趋势，其变异系数也变化不大，即在样本枣树振幅允许的范围内，振幅越大，每个红枣的最大加速度值也相对较大，越容易振落红枣；在相同振幅，不同路径，红枣的质量越大，红枣振动的瞬时加速度也相对较大，可知红枣的质量越大，振动过程中越容易振落。

表2 定频时红枣的加速度（振幅3、5、7 mm）

5 结 论

1）应用拉格朗日方程，建立红枣“枝—柄—果”的双摆振动模型，计算得系统在振动过程中的固有频率为14.69、17.26 Hz；

2）为获得不同果枝的共振频率，对选取的样本树进行了扫频试验，通过扫频试验结果分析得样本树的共振频率为12～24 Hz；

3）通过对样本树振动频率与瞬时加速度进行分析，枣树不同路径第一次发生共振频率13～18 Hz，与理论分析计算得到的振动频率基本一致；

4）通过对振幅为3、5、7 mm时红枣进行力传递效果试验：在一定的振幅范围内，振幅越大，红枣振动的瞬时加速度整体呈增大趋势，红枣所产生的瞬间惯性力越大，越容易振落，力的传递效果越明显。

[1] 魏文涛，高卫东，史玉光，等. 新疆地区气候与环境变化对沙尘暴的影响研究[J]. 干旱地理，2004，27(2)：137－141.

Wei Wentao, Gao Weidong, Shi Yuguang, et al. Influence of climate and environment change on dust storms in sinkiang[J]. Arid Land Geography, 2004, 27(2): 137－141. (in Chinese with English abstract)

[2] 付威，何荣，曲金丽，等.自走式矮化密植红枣收获机的设计[J]. 农机化研究，2014，36(4)：106－109.

Fu Wei, He Rong, Qu Jinli, et al.Design of self-propelled dwarf and close planting jujube harvester[J]. Journal of Agricultural Mechanization Research, 2014, 36(4): 106－109. (in Chinese with English abstract)

[3] 胡灿，鲁兵，侯书林，等. 新疆红枣收获机的研究现状与发展对策[J]. 中国农机化学报，2016，37(7)：222－240.

Hu Can, Lu Bing, Hou Shulin, et al.Research status and development countermeasures on harvesting machinery of jujube in Xinjiang[J]. Journal of Chinese Agricultural Mechanization, 2016, 37(7): 222－240. (in Chinese with English abstract)

[4] 张亚欧，坎杂，李成松，等.矮化密植红枣收获机捡拾装置的设计[J]. 农机化研究，2016，38(4)：71－75.

Zhang Yaou, Kan Za, Li Chengsong, et al.Design of dwarf and close planting jujube harvester pickup device[J]. Journal of Agricultural Mechanization Research, 2016, 38(4): 71－75. (in Chinese with English abstract)

[5] Loghavi M, Mohseni S H. The effects of shaking frequency and amplitude on detachment of lime fruit[J]. Iran Agricultural Research, 2005, 24(2): 27－38.

[6] Mateev L M, Kostadinov G D. Probabilistic model of fruit removal during vibratory Morello harvesting[J]. Biosystems Engineering, 2004, 87(4): 425－435.

[7] Castro-García S, Blanco-Roldán G, Gil-Ribes J, et al. Dynamic analysis of olive trees in intensive orchards under forced vibration[J]. Trees-Structure and Function, 2008, 22(6): 795－802.

[8] HeLong, Zhou Jianfeng, Du Xiaoqiang, et al. Energy efficacy analysis of a mechanical shaker in sweet cherry harvesting[J]. Biosystems Engineering, 2013, 116(4): 309－315.

[9] Upadhyyaya S K, Rand R H J, Cooke R. Dynamics of fruit tree trunk impact[J]. Transactions of the ASAE, 1981, 24(4): 846－855.

[10] Rand R H, Cooke J R.Vibratory fruit harvesting: A non-linear theory of fruit-stem dynamics[J]. Journal of Agricultural Engineering Research, 1970, 15(4): 347－363.

[11] Cooke J R, Rand R H. Vibratory fruit harvesting: A linear theory of fruit-stem dynamics[J].Journal of Agricultural EngineeringResearch, 1969, 14(3): 195－209.

[12] Parchomchuk P, Cooke J R. Vibratory harvesting: An experimental analysis of fruit-stem dynamics[J]. Transactions of the ASAE, 1971, 14(1): 20－24.

[13] Du X Q, Chen D, Zhang Q, et al. Dynamic responses of sweet cherry trees under vibration excitations[J]. Biosystems Engineering, 2012, 111(3): 305－314.

[14] 陈度，杜小强，王书茂，等. 振动式果品收获技术机理及研究进展[J]. 农业工程学报，2011，27(8)：195－200.

Chen Du, Du Xiaoqiang, Wang Shumao, et al. Mechanism of vibratory fruit harvest and review of current advanced[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(8): 195－200. (in Chinese with English abstract)

[15] 杜小强，倪柯楠，潘珂，等. 可调振幅单向拽振式林果采收机构参数优化[J]. 农业工程学报，2014，30(16)：25－32.Du Xiaoqiang, Ni Kenan, Pan Ke, et al. Parameter optimization of stroke-adjustable and monodirectional pulling fruit harvester[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(16): 25－32. (in Chinese with English abstract)

[16] 杜小强，倪柯楠，武传宇. 基于外旋轮线轨迹的果品振动采收机构研究[J]. 农业机械学报，2016，47(3)：59－66.

Du Xiaoqiang, Ni Kenan, Wu Chuanyu. Vibratory harvesting mechanism for tree fruit based on epitrochoid[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 59－66. (in Chinese with English abstract)

[17] 仇高贺，杜小强，武传宇. 基于ADAMS柔性体的山核桃树振动仿真研究[C]// 2012中国农业机械学会国际学术年会论文集.

Chou Gaohe, Du Xiaoqiang, Wu Chuanyu. Chinese hickory vibratory analysis base on rigid-flexible coupling dynamics[C]//Proceedings of the international academic annual meeting of China Agricultural Machinery Society 2012. (in Chinese with English abstract)

[18] 瞿维，王春耀. 受迫振动下杏果实树枝能量传递初探[J].西北农林科技大学学报：自然科学版，2014，42(7)：223－227.

Qu Wei, Wang Chunyao. Energy transfer of apricot fruit branch under forced vibration[J]. Journal of Northwest A&F University: Nat. Sci. Ed., 2014, 42(7): 223－227. (in Chinese with English abstract)

[19] 蔡菲，王春耀，王学农，等. 基于高速摄像技术的振动落果惯性力研究[J]. 西北农林科技大学学报：自然科学版，2013，41(4)：208－212.

Cai Fei, Wang Chunyao, Wang Xuenong, et al. Inertia force of fruits abscised by vibration based on high-speed video canera technology[J]. Journal of Northwest A&F University: Nat. Sci. Ed., 2013, 41(4): 208－212. (in Chinese with English abstract)

[20] 范雷刚，王春耀，刘春霞，等. 振动参数对果树采收影响的试验研究[J]. 农机化研究，2016，38(10)：165－168.

Fan Leigang, Wang Chunyao, Liu Chunxia, et al. Experimental study on the impact of vibration parameters on fruit trees[J]. Journal of Agricultural Mechanization Research, 2016, 38(10): 165－168. (in Chinese with English abstract)

[21] 王长勤，许林云，周宏平，等. 偏心式林果振动采收机的研制与试验[J]. 农业工程学报，2012，28(16)：10－16.

Wang Changqin, Xu Linyun, Zhou Hongping, et al. Development and experiment of eccentric-type vibratory harvester for forst-fruits[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(16): 10－16. (in Chinese with English abstract)

[22] 王业成，陈海涛，林青. 黑加仑采收装置参数的优化[J]. 农业工程学报，2009，25(3)：79－83.

Wang Yecheng, Chen Haitao, Lin Qing. Optimization of parameters of blackcurrant harvesting mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(3): 79－83. (in Chinese with English abstract)

[23] 王业成，陈海涛，邱立春. 黑加仑干枝的试验模拟分析[J]. 农业工程学报，2011，27(增刊2)：45－49.

Wang Yecheng, Chen Haitao, Qiu Lichun. Modal experiment analysis on blackcurrant branches[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(Supp.2): 45－49. (in Chinese with English abstract)

[24] 刘继展，唐善齐，单帅，等. 机器人采摘葡萄果穗振动仿真与试验[J]. 农业机械学报，2016，47(5)：1－8.Liu Jizhan, Tang Shanqi, Shan Shuai, et al. Simulation and test of grape fruit cluster vibration for robotic harvesting[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(5): 1－8. (in Chinese with English abstract)

[25] 朱晓东，金永磊. 参数激励双摆的建模与动力学分析[J]. 苏州大学学报：工科版，2007，27(3)：47－51.

Zhu Xiaodong, Jin Yonglei. Modeling of parametrically excited double pendulum and dynamical analysis[J]. Journal of Suzhou University (Enginering Science Edition), 2007, 27(3): 47－51. (in Chinese with English abstract)

[26] 原大宁，马建平，杨润，等. 基于双摆模型的单晶炉提拉系统摆动现象动力学分析[J]. 西安理工大学学报，2008，24(2)：177－181.

Yuan Daning, Ma Jianping, Yang Run, et al. Dynamic simulation of oscillation phenomenon of single-crystal growth furnace lifting system basedon double pendulum model[J]. Journal of Xi’an University of technology, 2008, 24(2): 177－181. (in Chinese with English abstract)

[27] 山本博昭，川村登. 柑橘の機械収穫に関する基礎研究（第2報）―振動中の果実－果梗系の力学と作用力について[J]. 農業機械学会誌，昭和50年4月，38(1)：53－62.

[28] 孙艳平，康庄，孙艳秋. 复杂椭圆形薄板和椭球体转动惯量[J]. 辽宁科技大学学报，2011，34(4)：352－354.

Sun Yanping, Kang Zhuang, Sun Yanqiu. Moment of inertia on complex oval plate and complex ellipsoid[J]. Journal of University of Science and Technology Liaoning, 2011, 34(4): 352－354. (in Chinese with English abstract)

[29] 郑兆昌，庞家驹，王勖成，等. 机械振动[M]. 北京：机械工业出版社，1980.

[30] Du X Q, Wu C Y, He L Y, et al. Dynamic characteristics of dwarf Chinese hickory trees under impact excitations for mechanical fruit harvesting[J]. Int J Agric & Biol Eng, 2015, 8(1): 17－25.

[31] 杨红英. 矮化密植红枣采收装置采收部件的设计及试验研究[D]. 石河子：石河子大学，2013.

Yang Hongying. Design and Experimental Study of Harvest parts of Dwarf and Close Planting Jujube Harvest device[D]. Shihezi: Shihezi University, 2013. (in Chinese with English abstract)

Simulation experiment in lab on force transfer effect of jujube under vibration excitation

Fu Wei, Zhang Zhiyuan, Liu Yudong, Pan Junbing, Cui Jian, Ding Kai, Zhang Huiming※

(832003,)

In recent years, jujube planting area in Xinjiang has been increasing, and jujube harvest depends entirely on manual work that is characterized by low efficiency and high cost, which has become the bottleneck of the sustainable development of Xinjiang jujube industry. Therefore, mechanized operation is in urgent need. In order to improve the efficiency of vibration harvesting for fruits to reduce power consumption in excitation, the effect of force transfer in vibration harvesting was studied based on the changes in instantaneous acceleration of fruits in vibration,. Aimed to vibration harvesting of jujube, the preset study analyzed natural frequencies in system vibration through simplifying “branch-stalk-fruit” of jujube to a double-pendulum vibration model firstly, and then constructed Lagrange’s double-pendulum multi-degree-of-freedom vibration equation, and the natural vibration frequencies of the system were obtained (14.69 and 17.26 Hz respectively). Based on electrodynamic vibration test stands, experiment of frequencies scanning was conducted for the whole jujube tree. In the resonance, with the gradual increase of the distance to excitation source, resonance frequency increased gradually. The resonant frequency of 3 test points in each path ranged from 12 to 24 Hz, which provided reference for constant frequency test. In order to investigate the effect of vibration frequency and amplitude on instantaneous acceleration of each branch of the sample tree, vibration test for constant frequency of jujube was carried out at the amplitude of 3, 5 and 7 mm, respectively, and the frequency of 12-24 Hz. DHDAS analysis showed a correlation between vibration frequency and instantaneous acceleration of jujube. The longer the distance to excitation source, the greater the change of instantaneous acceleration in resonance. Instantaneous acceleration showed no obvious changes with the increase of amplitude. The bifurcation point and diameter of the tree had great influence on the resonance amplitude; and the more the bifurcation points of the path, the smaller the change of instantaneous acceleration. The motion of jujube under forced vibration was analyzed using 3D (three-dimensional) high-speed camera technology to reveal the maximum instantaneous acceleration value of jujube in space. Statistical analysis demonstrated that the maximum instantaneous inertia force of jujube was greater than the maximum breaking load of fruit stalk (6 N). With the increase of amplitude, the maximum instantaneous acceleration of jujube increased gradually, and its variation coefficient did not change obviously. That was, within the range of the amplitude of the sample jujube tree, the maximum acceleration value of each jujube was relatively large and jujube was more likely to fall with the increase of amplitude. With the same amplitude and different paths, the larger the mass of jujube, the larger the instantaneous acceleration of jujube vibration, suggesting that large mass of jujube is correlated with easy falling in vibration. With different amplitudes and the same path, the smaller the trunk diameter of each path of the sample tree, the larger the average value of vibration acceleration of jujube, which suggested that trunk diameter was also one of the main factors affecting jujube vibration harvest. This study can provide a theoretical basis and technical reference for the design of the excitation system for jujube harvest.

vibration; mechanical properties; experiments; jujube; vibration frequency

10.11975/j.issn.1002-6819.2017.17.009

S233.75

A

1002-6819(2017)-17-0065-08

2017-04-24

2017-08-02

国家自然基金项目（51365049）；石河子大学高层次人才项目（4004303）；石河子大学青年人才项目（2013ZRKXYQ-YD22）

付威，博士，副教授，主要从事林果收获机械相关研究。石河子 石河子大学机械电气工程学院，832003。Email：fuwei001@126.com

张慧明，实验师，博士研究生，主要从事田间作业机械相关研究。石河子 石河子大学机械电气工程学院，832003。Email：a_an_07@qq.com