基于模糊神经网络的短时交通流预测方法研究

程山英

(江西科技师范大学 数学与计算机科学学院，南昌 330038)

基于模糊神经网络的短时交通流预测方法研究

程山英

(江西科技师范大学 数学与计算机科学学院，南昌 330038)

为满足交通控制和诱导系统的实时性需求，减少交通拥挤状况，降低交通事故突发频率，需要对短时交通流进行预测;当前的短时交通流预测方法是采用K-近邻的非参数回归对其进行预测，预测过程中没有将预测模型中关键因素对交通流的影响进行详细的说明，导致预测结果不准确，存在短时交通流预测误差较大的问题;为此，提出一种基于模糊神经网络的短时交通流预测方法;该方法首先以历史短时交通流数据样本序列为基础，将提取的关联维数作为短时交通流的混沌特征量，然后以该特征量为依据，对短时交通流数据进行聚类，使相同的短时交通流聚合类样本比不同的交通流聚合类样本更为贴近，采用高斯过程回归对短时交通流预测模型进行建设，建设过程中利用差分方法对短时交通流预测序列进行平稳化操作之后，对短时交通流预测模型进行训练，将GPR模型引入至短时交通流预测过程中，得到交通流预测方差估计值，并确定交通流预测值置信区间，由此实现短时交通流的预测;由此实现短时交通流的预测;实验结果证明，所提方法可以准确地预测交通运输系统的实时状况，为车辆行驶的最佳路线进行了有效引导，减少了自然影响方面和人为因素对短时交通流预测结果的干扰，为交通部门对交通路况的控制管理提供了依据。

模糊神经网络；短时交通流；预测方法

0 引言

如今，私家车越来越多，导致交通堵塞，以及交通事故突发的状况时有发生。而短时交通流预测不仅可以减少道路上突发状况的发生频率，而且还可以为出行者的路径选择和出行时间提供参考。是交通管理方面十分重要的组成部分[1-2]。也正是因为短时交通流预测的深远影响，使其成为了人们关注的热点问题[3]。但是由于短时交通流预测具有不确定性、灵活性、不稳定性等特点，导致大多数的预测方法无法对短时交通流进行高效、准确、稳定地预测，经常出现预测效果不理想，预测结果与实际路况偏差大等问题[4]。在这种情况下，如何增强短时交通流预测的稳定性，减少预测所用时间，提高预测的效率和准确性成为亟待解决的问题[5]。而基于模糊神经网络的短时交通流预测方法，可以对短时交通流进行安全、可靠有效地预测，是解决上述问题的可行途径[6]。鉴于短时交通流预测对人们日常生活具有很大的意义，所以引起了广大研究学者的高度重视，同时也出现很多优秀的预测方法[7]。

文献[8]提出了一种基于K近邻非参数回归的短时交通流预测方法。该方法首先对交通流的空间特征进行提取，利用特征提取结果对道路网进行划分，然后以划分结果为基础，采用Elman神经网络对道路网中的多断面短时交通流同时进行预测，最后以多断面短时交通流数据量为依据，对该方法进行验证。该方法预测效率较高，但是存在过程繁琐的问题。文献[9]提出了一种基于SVM的短时交通流预测方法。该方法首先利用SVM的独立成分，分析获得同一道路上各观测点交通流量独立源信号，然后采用支持向量机预测模型，对独立源信号进行预测与建模，最后依据遗传算法的优化参数将上述模型转化为短时交通流量数据，并获得预测结果。该方法虽然较为简单，但是存在预测结果偏差大的问题。文献[10]提出了一种基于ICA的短时交通流预测方法，该方法首先分析短时交通流的特性，从原理上描述非参数回归方法对短时交通流预测的适用性，然后依据应用非参数回归，对短时交通流预测的关键影响因素进行讨论，最后以讨论结果为依据，完成对短时交通流的预测。该方法虽然用时较短，但是存在预测效率低的问题。

针对上述产生的问题，提出一种基于模糊神经网络的短时交通流预测方法。仿真实验证明，所提方法可以对短时交通流进行准确有效地预测。

1 基于模糊神经网络的短时交通流预测方法

1.1 短时交通流混沌关联维特征提取与交通流数据聚类

为了提高短时交通流预测效率，以历史短时交通流数据样本序列为基础，将提取的关联维数作为短时交通流的混沌特征量，然后以该特征量为依据，对短时交通流数据进行聚类。交通流中的混沌特征一般表现为无明显规则与次序、非同期性复杂的折叠与扭曲，所以必须利用关联维数对交通流的混沌特征进行描述。

假设，将关联维数当作短时交通流聚类的混沌特征量，以短时交通流特征相空间的重构为依据，将相空间的一维时间序列在多维相空间中可以进行扩展。由此提取短时交通流混沌关联维特征。本文对短时交通流特征相空间的重构不做研究。利用对交通流特征相空间重构的分析，可以得到相空间的重构时间序列为：

Xi=(xi,xi+τ,…,xi+(m-1)τ)T

(1)

其中:Xi代表短时交通流特征相空间重构时间序列，i代表短时交通流特征数量，xi代表短时交通流特征相空间重构时间序列中的子集，τ代表影响上述相空间重构的参数，m代表相空间维数，T代表相空间重构的控制阈值。利用上述相空间重构中的m维相空间，相点xj除了到xi本身的距离可以远于r，否则不得远于r，则相点数目Q可表示为：

(2)

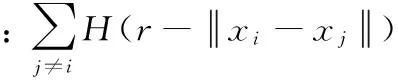
(3)

其中:N代表相空间重构中的向量数目，2代表为了排除重复的计数，CN(r)代表关联函数。利用范数对两个相点间的距离进行描述，由此可以获得两个相点间的距离，也可以称为两个矢量间最大的分差量：

(4)

N=m-(m-1)τ

(5)

对相点中存在的关联相点对数占全部可能的N(N-1)/2种配对比例进行计算，并将其称为关联维数，则有公式如下：

(6)

其中:Cm(r)代表上述中的关联维数，通过上述得到的关联维数，就是短时交通流聚类的混沌特征量，通过此关联维数完成短时交通流的聚类。短时交通流的聚类就是将短时交通流数据划分为几个类，使相同的短时交通流数据聚合类样本，比不同的短时交通流数据聚合类样本更为贴近。以上述的短时交通流混沌关联维特征为基础，对短时交通流数据进行聚类，具体过程如下。

假设，输入n个交通流数据样本{x1,x2,…,xn}，利用短时交通流混沌关联维特征，在上述样本中选取出U个短时交通流数据聚类中心，通过{z1,z2,…,zn}对其进行描述。

假设，将n个短时交通流数据样本通过下列原则，按顺序进行划分到距离最近的类别ωj中，则有公式为：

(7)

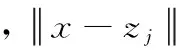
(8)

(9)

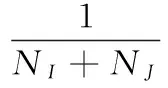
(10)

其中:zIJ代表短时交通流数据ωI、ωJ的合并中心，NI和NJ分别代表数据聚类的控制阈值，zI和zJ分别代表新的聚类中心。假设l>d2，则结束迭代。将有相同混沌关联特征的短时交通流数据依据上述过程合并成一类，由此实现短时交通流数据的聚类。

1.2 短时交通流预测

以1.1各项数据为基础，利用高斯过程回归对短时交通流进行预测。预测过程中，利用差分方法对短时交通流预测序列进行平稳化操作之后，对短时交通流预测模型进行训练，将GPR模型引入至短时交通流预测过程中，得到交通流预测方差估计值，并确定交通流预测值置信区间，从而完成对短时交通流的预测。则短时交通流的预测问题可表示为：

Yi+1=f(Xi)+ε

(11)

其中:Yi+1代表i+1时刻的短时交通流预测值，f(Xi)代表与第i+1时刻短时交通流的相关预测因子，f代表短时交通流的预测模型，ε代表未知短时交通流统计特性预测的噪声。

因为实际短时交通流预测序列，具有非平稳性，综上可知短时交通流的预测模型，有隐含零均值的假设，容易对短时交通流预测产生误差，所以需要采用差分法对交通流预测序列，进行稳定化处理之后再完成短时交通流预测模型的训练与预测，假设短时交通流预测序列为{Ai:i=1,…,n}，那么差分之后的预测序列为{▽BxO=xO-xO-B:O=B+1,B+2…}，式中,B代表差分间隔，O代表当前预测值，▽BxO代表第B+1时刻的短时交通流预测因子，为了将原有的短时交通流预测序列实现平稳化，必须先确定差分间隔B，依据时间序列的分析理论，可利用样本自相关函数对选取的短时交通流数据进行详细分析，将短时交通流数据样本的自相关函数估计值的相关周期，作为差分间隔B的估计值，则样本的自相关函数估计值可表示为：

(12)

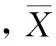
YO+1=xO-B+1+▽BxO+1=xO-B+1+h(▽BxO)

(13)

其中:YO+1代表第O+1时刻的短时交通流预测值，xO-B+1代表原短时交通流序列中第O-B+1时刻的预测值，h(▽BxO)代表短时交通流均值预测函数。综上所述，短时交通流预测方法如下：

1)对原有的短时交通流预测序列{Ai:i=1,…,n}，利用样本自相关函数得到样本ACF的估计值，并依据样本ACF估计的差分间隔B，转2)。

2)以原有的短时交通流预测序列为基础，得到差分序列{▽BxO=xO-xO-B:O=B,B+1,…}，对其进行归一化处理，并对公式(14)给出的数据集进行训练。

(14)

3)假设，短时交通流预测超参数初始值为θ0，在训练短时交通流数据集D时，计算出最佳超参数θ*。

4)进入短时交通流预测，依据对数据集的测试，获得短时交通流预测因子Bxm*=xm-xm-B，并将预测因子带入短时交通流预测模型中，得到预测值为ym + 1*=xm-B + 1+h*(Bxm*)，式中，h*(Bxm*)代表最佳超参数的表达式，综上所述，同样可对该次的短时交通流预测方差估计值进行计算。

5)对短时交通流预测误差进行计算，如果需要再次预测，则返回4)。

6)对累计的短时交通流预测误差进行计算，并对预测结果进行分析与评价，由此完成了对短时交通流的预测。

2 仿真实验结果与分析

为证明基于模糊神经网络的短时交通流预测方法的可行性，需要进行一次仿真实验。在Matlab的环境下搭建短时交通流预测实验仿真平台。实验数据取自于北京三环道路的全天交通流量，利用本文所提方法对实验数据进行预测，观察本文所提方法的整体有效性和可靠性。表1是不同方法下全天短时交通流预测的相对误差率(%)对比。相对误差率公式为：

(15)

表1 不同方法下全天短时交通流预测相对误差率对比

分析表1可知，文献[9]所提方法的全天短时交通流预测相对误差率，要高于本文所提方法的相对误差率，由于文献[9]所提方法在进行短时交通流预测时，利用SVM的独立成分，分析的是同一道路上各观测点交通流量独立源信号，并没有根据不同路径的具体情况进行分析，导致在进行短时交通流预测时，相对误差率较大，而本文所提方法在进行短时交通流预测时对各种短时交通流数据进行聚类，针对不同交通流数据类进行预测，所以相对误差率较小，证明本文所提方法在进行短时交通流预测时具有稳定性。表2是不同方法下，高峰时段的短时交通流预测相对误差率(%)对比。

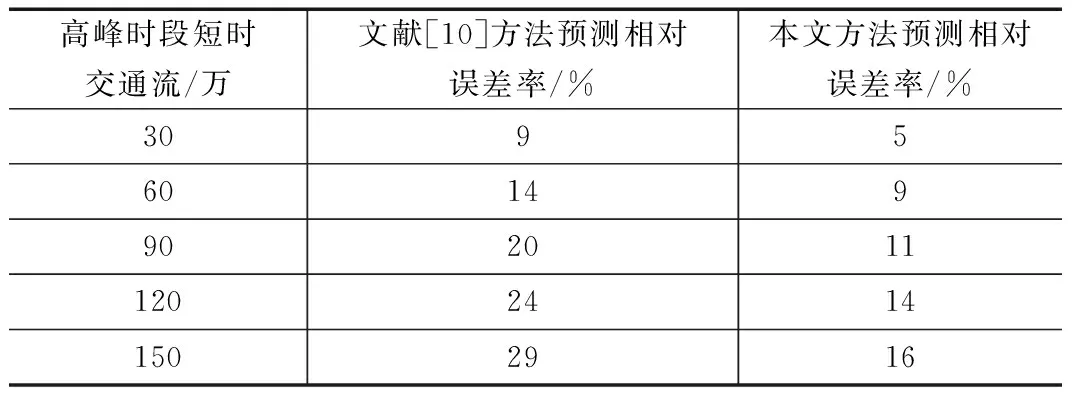
表2 不同方法下高峰时段交通流预测相对误差率对比

通过表2可以看出，在高峰时段，文献[10]所提方法下的短时交通流预测相对误差率较高。由于上下班属于路况的高峰期，所以短时交通流的预测相对误差率会比较大。文献[10]所提方法依据非参数回归，对短时交通流预测的关键影响因素进行讨论，以讨论结果为依据，完成对短时交通流的预测，并没有进行具体实验分析，由于讨论结果与实际应用得到的结果有很大差别，所以使文献[10]所提方法下的短时交通流预测效果不是很理想，存在预测的相对误差率较大的问题，依据表1对本文所提预测方法的分析，说明本文所提方法优于文献所提方法，证明本文所提方法具有可实践性。图1是不同方法下短时交通流预测耗时(s)对比。

图1 不同方法下短时交通流预测耗时对比

由图1可知，在相同数量的短时交通流下，本文所提方法在进行短时交通流预测时，耗时较少，文献[8]、文献[9]和文献[10]所提方法预测耗时较多，这主要是因为在利用本文所提方法进行短时交通流预测时，采用高斯过程回归法，并利用样本自相关函数法对选取的短时交通流数据进行详细分析，此操作减少短时交通流预测所用时间，提高预测效率，进一步证明本文所提方法的可扩展性。图2是不同方法下短时交通流数据聚类时间(s)对比。

图2 不同方法下短时交通流数据聚类时间对比

分析图2可知，文献[8]和文献[10]所提方法的短时交通流数据聚类时间，比本文方法的交通流聚类时间要多，文献[9]所提方法的聚类时间曲线波动虽然不大，但上升趋势很明显，与之相比的本文所提方法，在短时交通流数据为200万之前，聚类时间曲线略有上升趋势，但在200万之后得到了缓冲，聚类时间又有所减少，说明本文所提方法的数据聚类速度很快，为交通流的预测节省时间。图3是不同方法下短时交通流预测准确率(%)的对比。

通过图3可知，文献[8]所提方法在短时交通流预测准确率方面优于文献[9]和文献[10]所提方法，但是与本文所提方法做对比，预测准确率有一定的差距。本文所提方法相应的预测准确率较高，是因为利用对短时交通流的特征提取、交通流数据聚类等过程完成短时交通流预测。预测准确率变化曲线说明本文所提方法的适用性和实用性都很强，可以广泛地应用于短时交通流预测中。

图3 不同方法下短时交通流预测准确率对比

仿真实验证明，本文所提方法可以准确地对短时交通流进行预测，具有较好的稳定性和灵活性。

3 结束语

采用当前方法对短时交通流进行预测时，无法安全准确地对其进行预测，存在短时交通流预测偏差大的问题。提出一种基于模糊神经网络的短时交通流预测方法。并通过仿真实验证明，所提方法可以准确地对短时交通流进行预测，为该领域的钻研提供支撑和依据。

[1] 周 桐,杨智勇,孙棣华,等.分车型的高速公路短时交通流量预测方法研究[J].计算机应用研究,2015,32(7):1996-1999.

[2] 梁 轲,谭建军,李英远.一种基于MapReduce的短时交通流预测方法[J].计算机工程,2015,41(1):174-179.

[3] 康 军,段宗涛,唐 蕾,等.高斯过程回归短时交通流预测方法[J].交通运输系统工程与信息,2015,15(4):51-56.

[4] 张洪宾,孙小端,贺玉龙.短时交通流复杂动力学特性分析及预测[J].物理学报,2014,63(4):51-58.

[5] 杨春霞,符义琴,鲍铁男,等.基于相似性的短时交通流预测[J].公路交通科技,2015,32(10):124-128.

[6] 谭国平,刘如通,谭林风.基于车辆合作的拥塞检测机制研究[J].电子设计工程,2016,24(21):118-121.

[7] 袁 磊,梁丁文,蔡之华,等.基于正交差分演化无迹卡尔曼滤波的短时交通流量预测方法[J].计算机应用,2015,35(11):3151-3156.

[8] 黄 杰,李 军,郭 翔.递推SOM神经网络在短时交通流预测中的应用[J].公路,2015,36(4):1-5.

[9] 徐健锋,汤 涛,严军峰,等.基于多机器学习竞争策略的短时交通流预测[J].交通运输系统工程与信息,2016,16(4):185-190.

[10] 罗向龙,焦琴琴,牛力瑶,等.基于深度学习的短时交通流预测[J].计算机应用研究,2017,34(1):91-93.

Short-term Traffic Flow Prediction Method Based on Fuzzy Neural Network Research

Cheng Shanying

(College of Math and Computer of the Jiangxi Science & Technology Normal University, Nanchang 330038,China)

In order to satisfy the real time demand of traffic control and guidance system, reduce the occurrence of traffic congestion, reduce the frequency of traffic accident emergency, need to forecast the short-term traffic flow. Current short-term traffic flow prediction method is using K - nearest nonparametric regression to forecast and predict the process of no will be key factors in the prediction model of traffic flow in detail, the influence of lead to inaccurate prediction results, the problems of short-term traffic flow prediction error is bigger. For this, put forward a kind of short-term traffic flow prediction method based on fuzzy neural network. This method firstly on the basis of the history of short-term traffic flow data sample series, the extracted correlation dimension as a short-term traffic flow of the chaos characteristics, and then based on the characteristics, the clustering of the short-term traffic flow data and make the same short-term traffic flow aggregation class samples than the aggregation of different traffic flow class samples more press close to, by using the Gaussian process regression of short-term traffic flow forecasting model, using the finite difference method in the process of construction of short-term traffic flow forecasting sequences with smooth operation, after training for short-term traffic flow prediction model, introducing the Gaussian model to short-term traffic flow prediction in the process, get the traffic flow forecasting variance, and traffic flow prediction confidence interval were determined, thus realizing short-term traffic flow prediction. The realization of short-term traffic flow prediction. The experimental results show that the proposed method can accurately predict the transportation system of the real-time condition, the best way for vehicle is the effective guidance, reduces the impact on natural and human factors interference, the result of the short-term traffic flow prediction for the traffic department to provide a basis for the control of road traffic management.

fuzzy neural network; short-term traffic flow; prediction method

2017-04-21；

2017-05-09。

江西省科技计划指导性项目(2015ZBAB201007)；江西科技师范大学校级科研重点项目(2016XJZD006)； 江西省高校人文社会科学研究项目(TQ1505)。

程山英(1979-)，女，江西南昌人，硕士，讲师，主要从事智能交通方向的研究。

1671-4598(2017)08-0155-04

10.16526/j.cnki.11-4762/tp.2017.08.040

U491

A