基于信息融合的模拟电路故障的特征提取与融合方法
2017-11-01宝石,许军
宝 石,许 军
(装甲兵工程学院 控制工程系,北京 100072)
基于信息融合的模拟电路故障的特征提取与融合方法
宝 石,许 军
(装甲兵工程学院 控制工程系,北京 100072)
在模拟电路故障诊断中,故障特征的提取是一个非常重要的环节,其提取结果的好坏将直接影响最终的诊断正确率;对现有文献研究发现,每种特征提取方法单独使用时都有一定的局限性,为了能够更加充分地提取模拟电路故障特征,提出了小波包分析与主元分析并行应用的方法,并将两种方法提取的特征向量依据不同规则进行了三种类型的融合,方便对比实验;为获取最优小波特征,提出了特征偏离度,并以此为标准选择最优小波基;最后,通过设计一种改进的神经网络分类器模型,将融合后的三种特征向量送入其中进行仿真验证,得出最终诊断结果;结果表明,该方法能够有效克服单一特征提取方法提取不充分的缺点,提高故障诊断的正确率,并且融合因子μ适中时诊断正确率最高。
特征提取;特征融合;故障诊断
0 引言
在模拟电路故障诊断研究中,如何快速、有效、全面地提取反映电路状态的故障信息特征,是进行电路故障诊断和测试的难点和关键。目前常用的故障特征提取方法种类很多,如时、频域特征法、主元分析法(PCA)、小波分析法、基于统计理论的特征提取法、EDM分解、局域均质算法(LMD)等[1]。每种方法都有自己的优点,同时也有一些不足,使用时往往不能充分提取故障特征,导致丢失部分细节信息或特征向量维数较高等。本文利用信息融合的思想,将主元分析法和小波包分析法并行同时应用,相互取长补短,能够有效提高故障样本提取效率。通过构建不同融合模型和验证不同融合因子,设计对比实验。最后,将融合后特征向量送入设计好的神经网络分类器进行训练和诊断[2]。该方法尽可能多地利用了故障样本信息,以此来保证最终的结果能够更加准确。
1 模拟电路故障特征提取方法
1.1 主元分析法
主元分析法作为模拟电路故障诊断特征提取方法,能够在提取主要故障特征的同时对一些高维样本进行降维处理[3]。
设原始数据样本为X=(xij)m×n,m为每个样本数据维数,n为样本个数。对X进行标准化处理,得到标准化数据矩阵Y=(yij),其中:
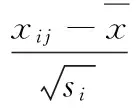
(1)
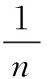
利用matlab软件计算出矩阵R的特征值λi和对应特征值的特征向量ai(i=1,2,…m)。将λi从大到小进行排λ1≥λ2≥λ3≥…λm,计算前面r个特征值的累计主成份贡献率。
(2)
选取累计方差贡献率达到90%以上的前r个特征值对应的特征向量构成特征子[4]。
1.2 小波包分析法
与小波分析相比较,小波包可以对其没有完成细分的高频部分进行进一步分解,从而精确地刻画出信号在各个频带下的局部信息,更有效的提取电路的故障特征[5]。因此,小波包变换可以将各频带上变化不明显的频率特征以显著的能量变化形式表现出来,再据此能量构造各故障模式下的特征向量。具体步骤如下:
1)对输出信号s进行n层小波包分解,提取共2n个小波包分解系数Xi。
2)依据各个小波包系数,重构各频带信号Si。
(3)
3)计算各频带信号的总能量。Ei表示Si的能量。则:
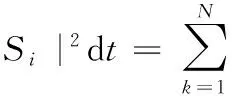
(4)
其中:xi(k)为Si的离散点的幅值,频带内信号个数(长度)为N。
4)根据Ei构造一个以能量为元素的特征向量T,并进行归一化处理[6]。
T=[E0,E1,…E2n-1]
归一化后,
t=[E0,E1,…E2n-1]
其中,
(5)
1.3 最优小波基的选择
在进行小波包分解时,小波基函数的种类对分解结果有很大的影响。因此,所选的小波基是否最佳对特征提取的重要性不言而喻。特征偏离度Db表示的是故障特征与正常状态特征之间的偏离程度。本文将以此作为选择标准来确定最优小波基[7]。
(6)
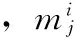
2 基于信息融合的特征提取和融合方法
小波包变换和主元分析从不同角度对输出信号进行特征提取,为了能够更加充分和全面的利用故障样本中所包含的信息,避免使用单一方法所带来的不足,文中将两种方法并行应用,并对提取到的特征进行有效的融合,以达到更佳的分类效果。图1是特征提取与融合的过程框图。
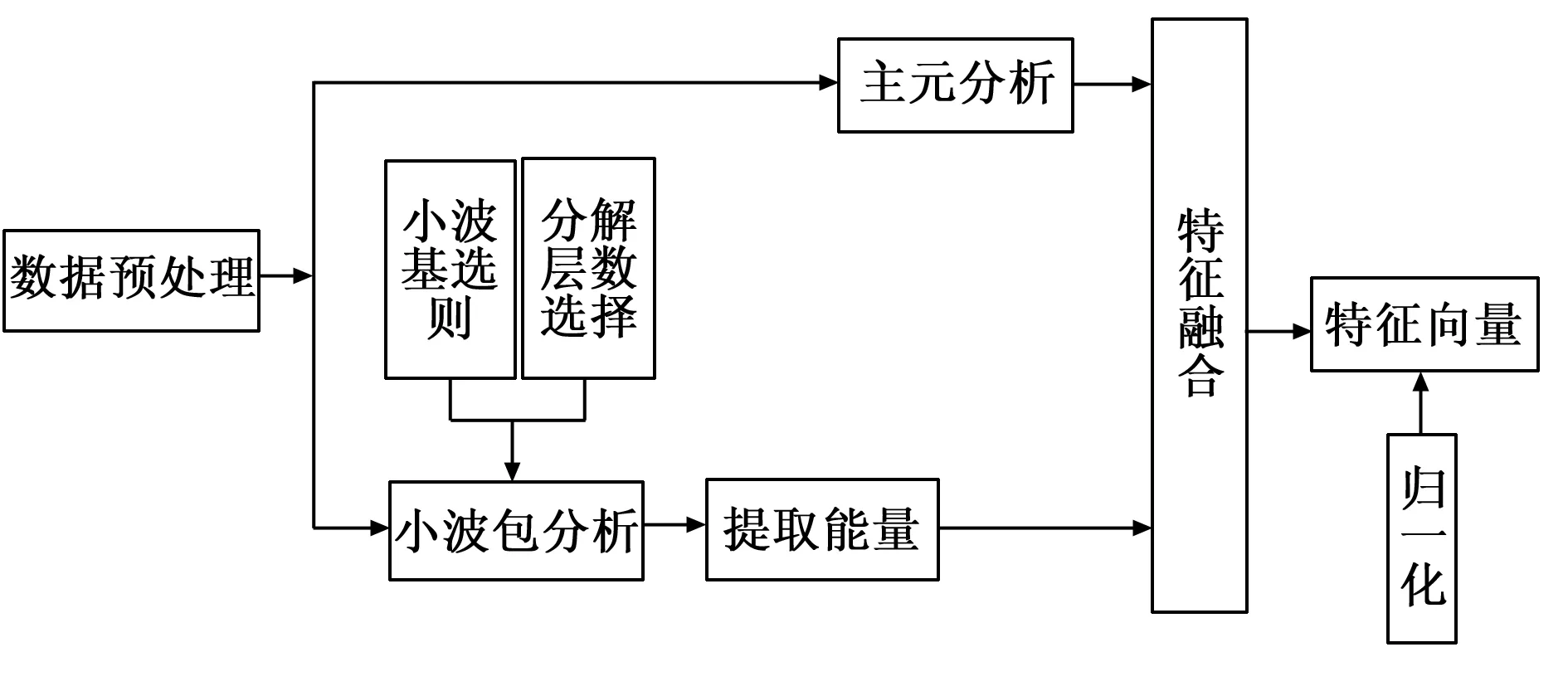
图1 特征提取与融合框图
具体方法步骤如下:
1)对待诊断电路用Mutisim软件进行建模,进行灵敏度分析,选择灵敏度较大的元件进行故障设置。
2)对采集到样本数据进行预处理,将其与标准响应信号做差,得到差值信号[8]。
原始样本数据为X=(x1,x2,…xn),无故障标准信号的数据样本为(xs)m×1,m为样本维数,n为样本个数,则预处理后样本为Xd=(x1-xs,x2-xs,…,xn-xs)。
3)对差值信号进行PCA特征提取,根据主成分贡献率选择合适的主元个数,构建新的特征向量。主元个数的选取要适中,过多或过少都不利于对信号的特征提取。
4)对差值信号进行小波包能量提取。首先确定最优小波基函数以及分解层数,计算各个频带的能量并归一化,构成特征向量。
5)将PCA特征和小波能量特征进行融合,形成融合后的特征向量,并对其进行归一化处理,送入分类器进行诊断。本文提出了三种不同的融合模型,同时还研究了不同融合模型因子μ对结果产生的影响。
假定PCA选取的主元个数为r,最终构成了一个r维特征向量a=[a1,a2,…,ar]T;小波包分解层数为n,最终提取的能量特征向量为t维,即特征向量b=[b1,b2,…bt]T;分别验证以下三种融合模型结果。设融合后特征向量为c。其中,0<μ<1,β=1-μ。
1)整体间隔模型:
2)单间隔模型:
3)双间隔模型:
为了避免数据大小不平衡带来的不利影响,同时保证下一步分类快速方便,将融合后特征向量c进行归一化处理得到c*,将其变为[0,1]之间数据,归一化方法如下[9]:
cmax表示样本ci中最大值,cmin表示样本ci中最小值。
3 仿真验证
本文中实验举例选用国际标准的测试电路Sallen-Key带通滤波器电路进行验证。按照上述故障特征提取和融合方法完成后,送入神经网络分类器进行故障诊断并验证结果。本文中使用的仿真软件为Mutisium10.0,算法的实现由Matlab R2013a完成。图2为Mutisium仿真的电路图模型。
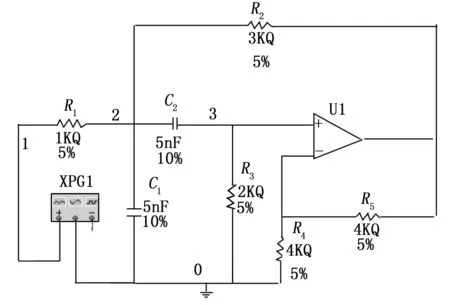
图2 带通滤波器电路图模型
其中各个元件的标称值分别为R1=1 kΩ,R2=3 kΩ,R3=2 kΩ,R4=R5=4 kΩ,C1=C2=5 nF 。电阻的容差为5%,电容的容差为10%。节点1为输入激励点,节点5为唯一输出响应点。实验中,激励信号选择基频为10 kHz,幅值为5 V,占空比10%的方波信号。下面按照实验步骤进行实验验证:
1)首先进行灵敏度分析[10],从而确定故障集。图3是各个元件对输出响应点5的灵敏度仿真分析结果图。
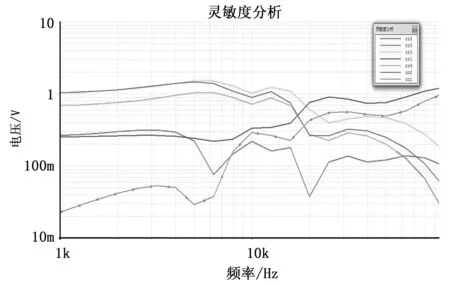
图3 灵敏度分析结果图
图中横、纵坐标分别为频率和输出响应电压。通过灵敏度分析可以看出R2,R3,C1,C2灵敏度较高。因此选取故障集包括R2↑,R2↓,R3↑,R3↓,C1↑,C1↓,C2↑,C2↓和正常模式共9种故障模式,令正常模式为M0,其余依次为M1-M8。表示元件参数在[+5%(+10%),+50%]之间,表示元件参数在[-5%(-10%),-50%]之间。本文中进行故障设置时,统一将其偏离幅度设置为50%。
2)在Multisim10.0仿真环境下分别对各种故障模式进行40次蒙特卡洛分析,得到原始采样数据。其中25次用于训练,15次用于测试。图4是时40次蒙特卡洛仿真分析图。其中元件参数变化服从高斯分布。
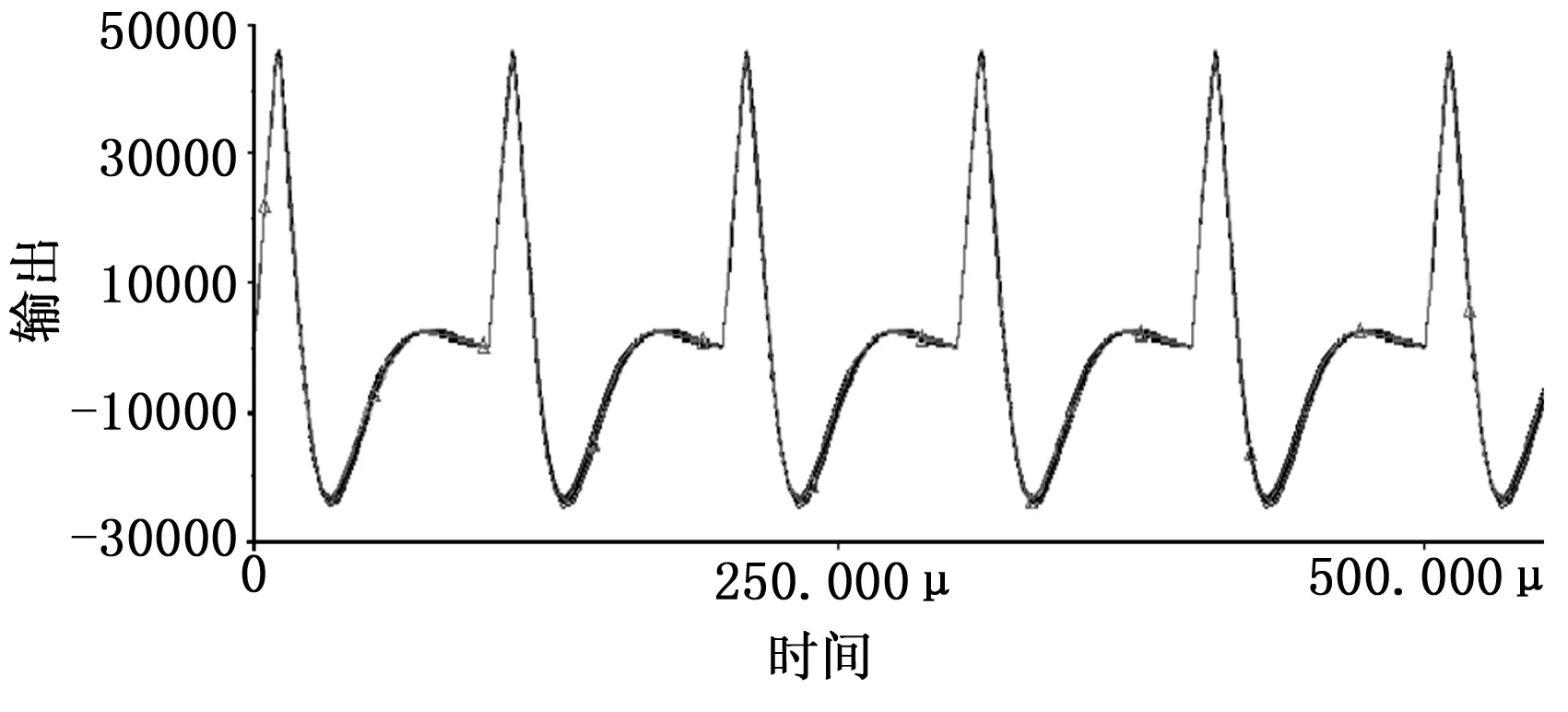
图4 R2↓时40次蒙特卡洛图
这样得到的是一个连续的响应曲线。为了便于分析和处理,我们对其进行采样,一共采集200个点,得到一个规模为200×360原始数据。然后与标准信号做差,得到差值信号,留待下一步分析。
3)对信号进行特征提取。
(1)对差值信号进行PCA特征提取。在Matlab中对预处理后的样本数据进行主元分析,所利用的程序代码如下:
[coeff,score,latent,tsquared,explained]=pca(P)
其中,P为样本数据矩阵,latent为特征值矩阵,score主成分分数,explained主元方差贡献率。
通过分析发现,当主元个数为8时,累计主元贡献率已达99.1%,远远超过90%。所以PCA提取的特征向量样本维数为8即可。
(2)对差值信号进行小波包能量提取。首先根据公式(6)进行最优小波包选取,本文选择Haar、db2、db3三种小波基函数进行特征偏离度计算。部分结果如表1。
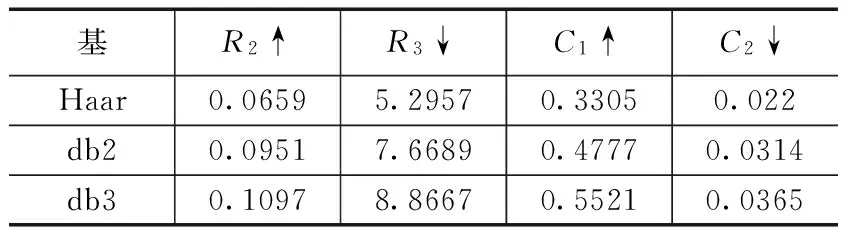
表1 不同小波基特征偏离度
从表中可以看出,db3小波基特征偏离度明显大于前两种,因此本文选择db3小波基函数。
利用Matlab小波工具箱中db3小波基函数对预处理信号进行3层小波包能量特征提取,分别计算出8个频带内的能量,归一化后得到8维特征向量[11]。主要程序代码如下:
clear;
clc;
t=wpdec(x,3,'db3','shannon');
plot(t);
for i=1:8;
cfs=wpcoef(t,[3,i-1]);
rcfs=wprcoef(t,[3,i-1]);
E(i)=norm(rcfs.^2)
end
[e,ps]=mapminmax(E)
图5为小波包分解结构和节点(3,1)的信号波形图。
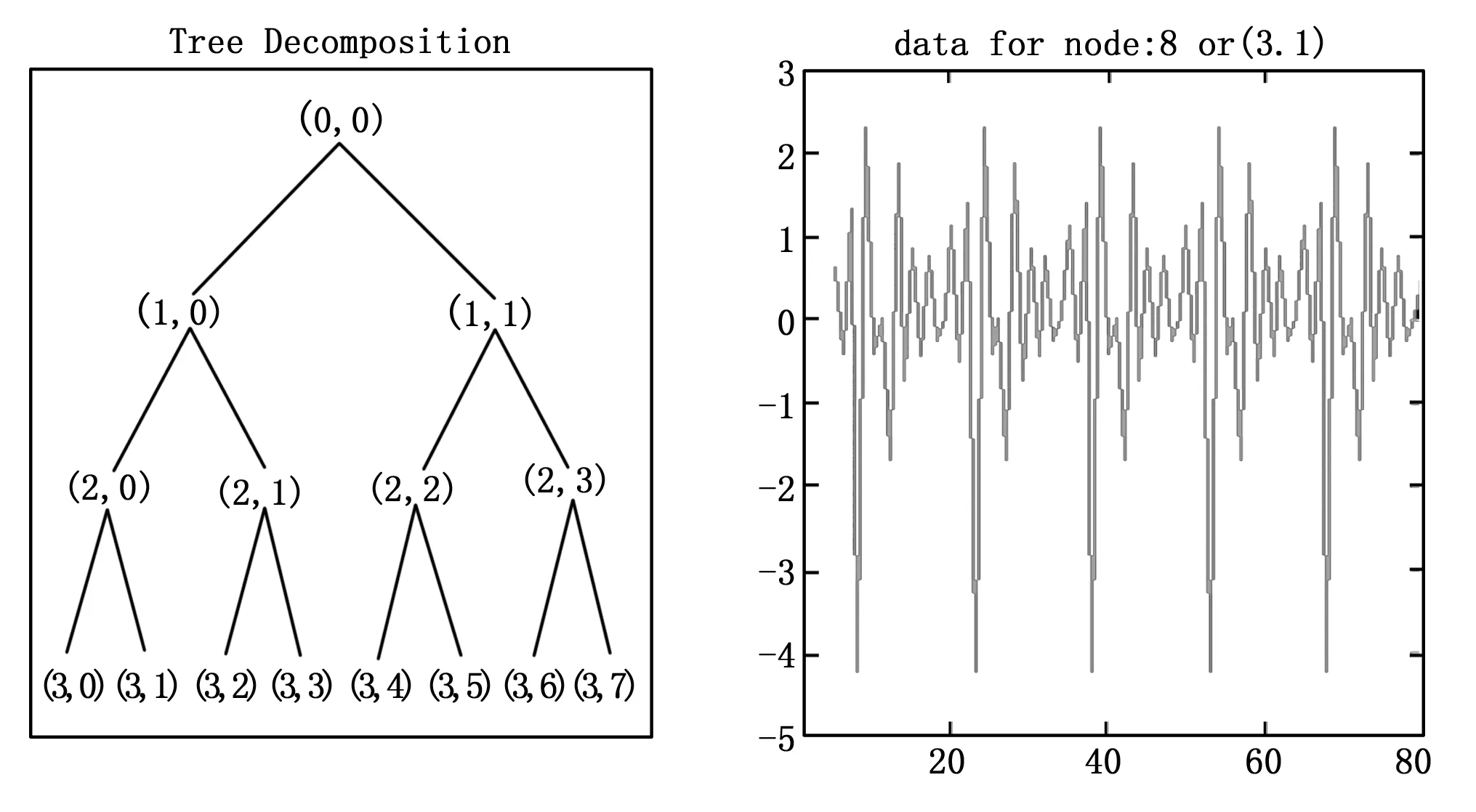
图5 三层小波包分解树
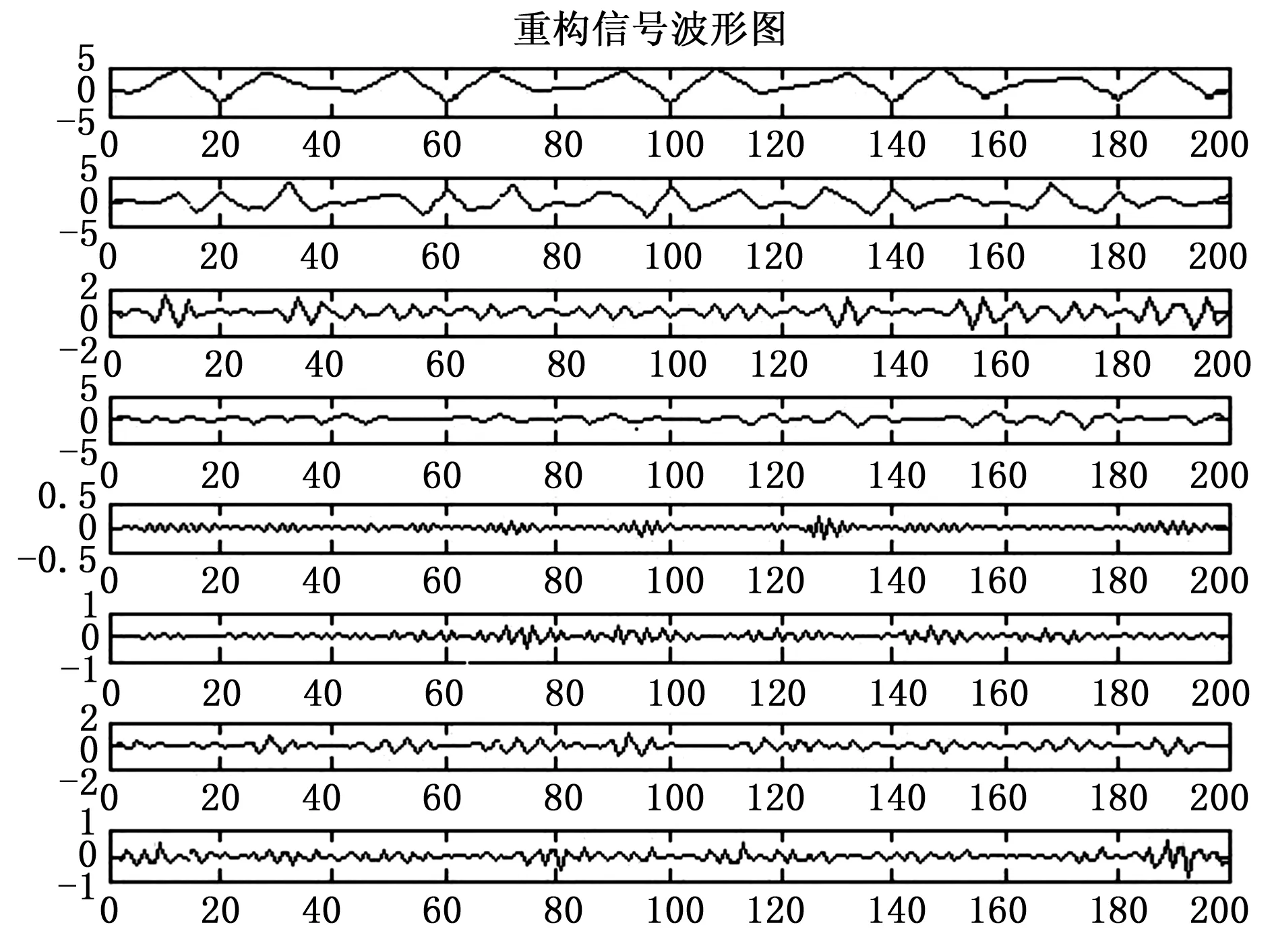
图6 重构信号波形图
建立:
net=newff(PR,[14,4],{‘tansig’’logsig’},’traingdm’);
训练:[net,tr]=train(net,P,T);
仿真:y=sim(net,P);
利用225组训练数据对神经网络进行训练学习,然后用另外135组测试数据进行结果验证。各种故障模式下神经网络期望的二进制输出如表2所示。
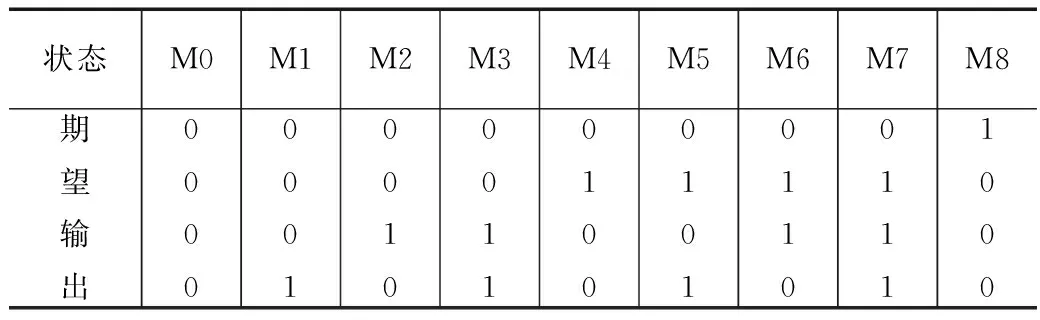
表2 神经网络期望输出二进制表
5)仿真结果对比分析。
下表是不同融合模型因子对应的诊断正确率。
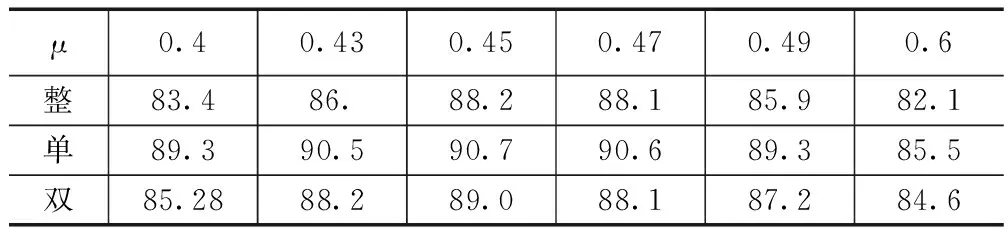
表3 不同融合因子对应诊断正确率 %
融合因子μ越大,说明PCA特征在融合后特征向量中占比越多。从表中可以看出,μ过大或过小都不会有最佳融合效果,当在0.46左右时,每种模型的诊断正确率都达到高。而相对比较,单间隔模型诊断正确率最高。
下表是μ=0.46,时,各种诊断方法正确率对比结果,特征融合采用单间隔模型。
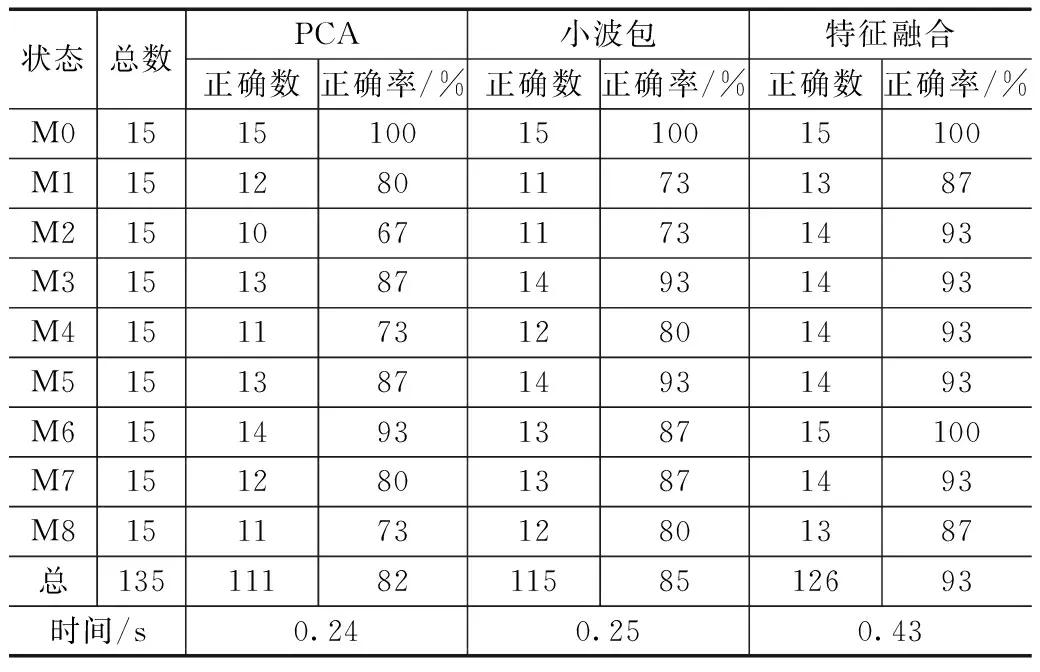
表4 测试样本诊断结果对比
可以看出,虽然诊断时间变长,特征融合模型的诊断正确率明显高于其单独使用时的诊断正确率。对于实时性要求不是非常高的模拟电路故障诊断来说,这种方法还是很有意义的。
4 结论
本文利用信息融合的思想,采用了主元分析与小波包分析并行提取故障特征的方法,并按照三种不同的融合模型进行了特征向量的融合。通过设计改进的神经网络分类器模型来对融合后特征向量进行故障诊断与结果验证。通过仿真计算,结果表明,该方法可以有效提高故障诊断正确率。
[1] 唐静远.模拟电路故障诊断的特征提取及支持向量机集成方法研究[D].成都:电子科技大学,2009.
[2] 廖 薇,许春冬,刘锦高.基于神经网络的模拟电路故障诊断研究[J].微电子学与计算机,2010,27(5).
[3] Aminan M, Aminan F.Neural network based analog-circuit fault diagnosis using wavelet transform as preprocessor[J].IEEE Trans on Circuits Syst-Ⅱ,2000,44(3):151-156.
[4] 陈绍炜,吴敏华,赵 帅.基于PCA和ELM的模拟电路故障诊断[J].计算机工程与应用,2015,51(11).
[5] 谢 涛.基于(多)小波(包)、神经网络及优化的模拟电路故障诊断研究[D].长沙:湖南大学,2011.
[6] 孙永奎.基于支持向量机的模拟电路故障诊断方法研究[D].成都:电子科技大学,2009.
[7] 何 星,王宏力,陆敬辉.基于优选小波包和ELM的模拟电路故障诊断[J].仪器仪表学报,2013,34(11):14-19.
[8] 吴明岩.基于信息融合的模拟电路故障诊断研究[D].大连:大连理工大学,2011.
[9] 唐圣学,蔡红军,李志刚.基于小波与神经网络的模拟电路故障诊断融合方法[J].2015,46(1).
[10]刘美容,张立玮.基于小波分解和模糊聚类的模拟电路软故障诊断[J].微电子学与计算机,2014,31(12).
[11] 潘 强,熊 波.基于灵敏度特性函数的特征提取与故障诊断[J].电子测量技术,2014(1):122-126.
[12] 吴 凡,张 莉. 基于小波神经网络的模拟电路故障诊断技术[J].计算机测量与控制,2014,22(11).
Feature Extraction and Fusion Method for Analog Circuit Fault Based on Information Fusion
Bao Shi, Xu Jun
(Academy of Armored Forces Engineering,Beijing 100072,China)
In the fault diagnosis of analog circuits, the extraction of fault features is a very important link, and the result of extraction has a direct impact on the final correctness of fault diagnosis.Because of the limitation of single fault feature extraction and to extract the fault characteristics more fully ,a method of fault feature extraction based on wavelet packet analysis and principal component analysis (PCA) is proposed, and three different feature vector fusion models are proposed. In order to obtain the optimal wavelet feature, the characteristic deviation degree is proposed, and the optimal wavelet basis is selected as the standard. Finally, an improved neural network classifier model is constructed, and the results of the fusion are sent into it to verify the results. The specific algorithm and simulation examples are given in this paper, The results show that the proposed method can effectively improve the correctness of fault diagnosis compared with single fault feature extraction method, and when the fusion factor is moderate, the correctness of diagnosis is the highest.
feature extraction; feature fusion; fault diagnosis
2017-02-22;
2017-03-10。
宝 石(1992-),辽宁阜新人,硕士研究生,主要从事检测技术与自动化装置方向的研究。
1671-4598(2017)08-0001-04
10.16526/j.cnki.11-4762/tp.2017.08.001
TP273
A
