张力腿筋腱桩基水平安装误差影响分析
2017-11-01,,,,
,,,,
(1.中海石油(中国)有限公司深圳分公司,深圳 518000;2.中国船级社海工技术中心,北京 100007)
张力腿筋腱桩基水平安装误差影响分析
高静坤1,王一江1,梁园华2,韦斯俊2,孙政策2
(1.中海石油(中国)有限公司深圳分公司,深圳 518000;2.中国船级社海工技术中心,北京 100007)
在设计海况下,计算张力腿平台筋腱桩基在不同水平安装误差情况下的张力时历,由此得到桩基水平安装误差距离与张力关系,根据该结果计算不同重现期海况中筋腱桩基水平安装误差对张力的修正值。根据整体性能分析得到的张力结果对筋腱强度进行校核,同时考虑安装误差修正项的影响。认为,在进行整体性能的筋腱张力和强度分析时,考虑筋腱桩基水平安装误差很重要。
张力腿平台;筋腱桩基;安装误差;修正
目前用于张力腿平台(TLP)锚固基础形式包括桩基、重力式基础、吸力基础、浅基础等,也可以是各种基础形式的组合[1-3]。筋腱将平台和桩基础连接,平台主体受到的载荷通过筋腱传递到桩基础进而传递给地基。张力腿筋腱可以直接与桩基础连接,也可以通过基盘与桩基连接,组成独立式的群桩基础。桩基础不仅受到张力筋腱的拔拉力,且作为置于海洋中的结构承受着包括地震等各种载荷。桩基础的设计选择及其安装制造方法对张力腿平台整体的工作性能有极大的影响[4]。桩基安装精度也会影响张力筋腱载荷传递,从而影响张力腿平台在复杂海洋环境载荷中的整体性能。目前,国内的研究更多地关注桩基础在海底受到土壤作用对其结构的影响[5-6]。而关于桩基安装对筋腱及平台性能的研究较少。针对TLP采用筋腱直接与桩基础连接的形式,联合利用水动力分析软件HARP和海洋工程分析软件Orcaflex,以中国南海海域对水深在400 m左右某潜在开发油田为例,对张力腿筋腱桩基水平误差影响进行分析。
1 计算原理和方法
1.1 耦合计算原理
TLP整体性能采用时域耦合方法进行模拟,首先使用频域方法计算平台水动力系数和波浪激励力,然后与张力腿筋腱和立管系统耦合进行时域动态求解。平台的一、二阶波浪激励力、附加质量系数和附加阻尼系数都可以在频域内求解,然后整个TLP系统的耦合动力计算可在时域内进行。TLP系统的时域运动方程为[7]
(1)
式中:M表示广义质量矩阵;A∞表示无穷频率附加质量矩阵;X表示平台位移矢量;K(t)表示延迟函数矩阵;D表示线性阻尼系数矩阵;C表示平台回复力系数矩阵。方程右边的外力FExternal(t)可以写为
FExternal(t)=F1st(t)+F2nd(t)+Fwind(t)+
Fcurrent(t)+Fmoor(t)
(2)
式中:F1st(t)和F2nd(t)分别为一、二阶波激力;Fwind(t)为风力;Fcurrent(t)为流力;Fmoor(t)为筋腱、立管系统的回复力。
方程(1)中的水动力系数和波浪激励力等可根据三维势流理论求得,再通过傅里叶逆变换得到时域的结果,求解时域耦合运动方程即可得到TLP整体性能。本文利用HARP完成TLP的动态耦合计算。
1.2 筋腱强度校核方法
TLP筋腱强度校核分析目的是对在位状态下的平台系泊筋腱的强度进行校核,确保筋腱在设计环境条件下满足要求。根据API RP 2T中的推荐作法,需计算A、B、S 3个安全等级的筋腱利用比因子(UR)和相互作用比因子(IR)来校核其强度是否满足要求。
根据API RP 2T,可以依据工作应力法(WSD)和载荷抗力法(LRFD)计算筋腱利用比因子UR和相互作用比因子IR,UR和IR应小于1。
1.2.1 WSD法
IR=A2+B2η+0.6|A|B≤1.0
(3)
UR=A=(ft+fb)SFt/Fy
(4)
B=fhSFC/Fhc
(5)
η=5-4Fhc/Fy
(6)
式中:ft为张力引起的筋腱轴向拉伸应力;fb为弯矩引起的筋腱弯曲应力;fh为静水压力引起的筋腱环向应力;Fhc为临界环向屈曲应力。
筋腱弹性环向屈曲应力Fhe为
Fhe=0.88E(t/D)2
(7)
式中:D为筋腱外径;t为筋腱壁厚;E为筋腱材料弹性模量。
如果Fhe<0.55Fy(弹性屈曲),Fhc=Fhe。
如果Fhe≥0.55Fy(非弹性屈曲),
Fhc=0.7Fy(Fhe/Fy)0.4≤Fy。
公式中的张力安全系数SFt和静水力压溃系数SFC,可以根据API RP 2T选取。
1.2.2 LRFD法
IR=A2+B2η+0.6|A|B≤1.0
(8)
A=(ft+fb)/(φtFy)
(9)
B=fh/(φhFhc)
(10)
公式中的系数与WSD法一致。校核过程中筋腱张力按下式进行计算。
T=L1Tmargin+L2Tpre+L3(Ttide+Tmean+Tdyn)
(11)
式中:Tmargin为张力余度修正,包括筋腱桩基水平安装误差;Tpre为筋腱预张力;Ttide为筋腱张力的潮汐修正;Tmean为平均环境载荷引起的平均筋腱张力;Tdyn为动态张力响应部分。
式(11)中的载荷和抗力因子可以根据API RP 2T选取。
2 数值计算模型
2.1 筋腱参数
张力腿平台每个立柱上设计布置2根张力腿筋腱,总共8根。张力腿筋腱由不同部分的圆柱形钢管密封而成,每根筋腱由顶部、底部连接段和若干段长度相同的主体段构成。顶部连接段用于筋腱与平台Porch连接固定,底部连接段用于筋腱与桩基接收器的连接,主体段将顶部和底部连接段在海水中连接成完整的张力腿筋腱。筋腱参数和安装坐标见表1。

表1 张力腿平台筋腱参数及导览孔坐标
2.2 数值计算模型
张力腿平台系统的动态耦合分析需要利用HARP软件完成,在HARP中建立张力腿平台与筋腱、立管系统的耦合模型,见图1。利用Orcaflex进行桩基水平安装误差分析和筋腱强度分析,数值模型见图2。根据HARP耦合计算结果筛选出张力最大的#1号和#5号筋腱作为分析的关键筋腱。
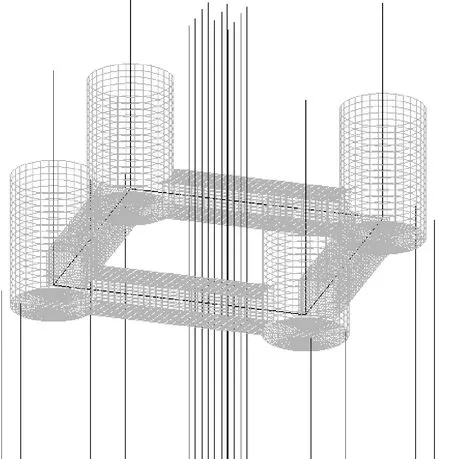
图1 张力腿平台耦合分析模型

图2 张力腿平台筋腱桩基误差和强度分析模型
3 计算结果
3.1 筋腱桩基水平安装误差对筋腱张力的影响
在进行桩基安装误差分析时,假设桩基安装误差变化范围在0.15~0.90 m,间隔0.15 m,计算张力腿平台在不同设计海况下,不同安装误差的筋腱张力时历结果。桩基误差对筋腱预张力的影响见图3,桩基安装偏离设计位置越远,安装误差越大,筋腱预张力较设计初始预张力逐渐增大。
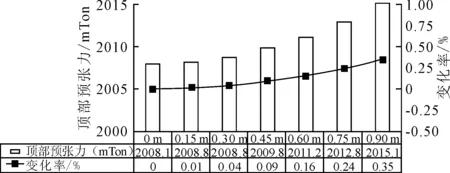
图3 桩基水平误差对筋腱预张力影响
各设计海况中筋腱桩基水平误差影响结果见图4~6。图4~6中“max变化值”表示有安装误差的张力最大值与准确安装张力最大值的差值,“min变化值”表示有安装误差的张力最小值与准确安装张力最小值的差值。“max变化率”等于“max变化值”与准确安装张力最大值的比值,“min变化率”等于“min变化值”与准确安装张力最小值的比值。

图4 一年一遇海况中桩基水平误差对筋腱张力极值影响

图5 百年一遇海况中桩基水平误差对筋腱张力极值影响

图6 千年一遇海况中桩基水平误差对筋腱张力极值影响
由图4~6可见,同样的安装误差量,在不同的海况中导致张力最大值和最小值变化不一样:例如,对于0.30 m(1 ft)桩基水平安装误差,一年一遇海况张力最大值变化81.1 mTon,百年一遇海况张力最大值变化206.3 mTon,千年一遇海况张力最大值变化265.8 mTon。由此可见,同样的安装误差,越恶劣的海况筋腱张力极值变化越大。
在海况不变的情况下,安装误差量越大对筋腱张力极值的影响越大:一年一遇海况中,最大值变化率由1.74%增大为10.81%,最小值变化率由1.53%增大为10.35%;百年一遇海况中,最大值变化率由3.38%增大为20.73%,最小值变化率由4.09%增大为24.73%;千年一遇海况中,最大值变化率由3.66%增大为22.63%,最小值变化率由2.77%增大为23.33%。
3.2 筋腱强度校核分析
由方程(11)可知,筋腱张力分量Tmargin包括筋腱桩基水平安装误差。在筋腱强度校核时,需要考虑桩基水平安装误差影响,根据3.1结果对张力进行修正。校核筋腱强度时,考虑桩基安装误差为0.30 m和0.60 m的余度修正。例如,0.30 m安装误差修正:对于一年一遇海况Tmargin增加81.1 mTon余度修正,百年一遇海况Tmargin增加206.3 mTon余度修正,千年一遇海况Tmargin增加265.8 mTon余度修正。
考虑桩基安装误差后筋腱强度校核结果见表2,图7为筋腱强度校核得到的利用比因子UR和相互作用比因子IR沿筋腱高度方向的变化。由表2可见,在校核筋腱强度时考虑桩基水平安装误差修正计算得到的校核系数UR和IR要大于没有误差修正的值。同样的误差水平,海况条件越恶劣,误差对筋腱强度的影响越大。例如,按照WSD法计算UR,考虑安装误差计算得到的因子要大4%~9%。如果没有误差修正,计算得到的UR和IR值达到0.95,那么考虑桩基安装误差后校核的结果就无法满足设计要求。所以在设计阶段,筋腱强度校核时考虑桩基水平安装误差修正,是一个更为合理安全的做法。由图7可见,校核计算得到的UR和IR在每个连接处会发生突变,原因是整根筋腱由不同部分连接而成,在每个连接处因为截面不一致,会产生应力集中,在强度校核时更应注意。
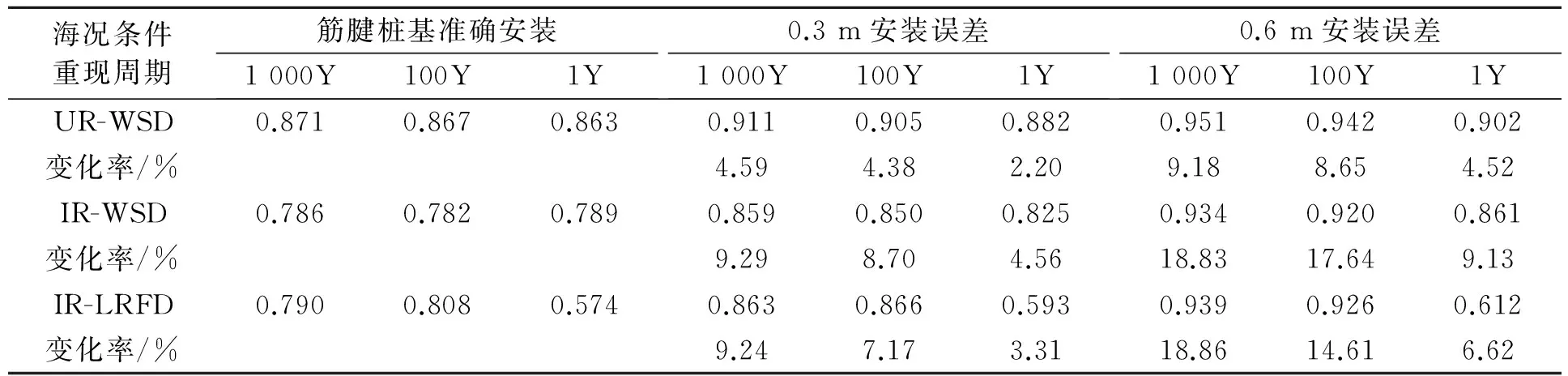
表2 筋腱强度校核结果

图7 桩基水平误差0.3 m筋腱强度校核结果——UR和IR沿筋腱长度分布
4 结论
1)桩基水平安装误差对筋腱张力极值的影响不可忽略,桩基水平安装误差能显著增大筋腱顶部最大张力或者减小筋腱底部最小张力。同样的安装误差,海况越恶劣,筋腱张力极值受到的影响越大,在设计时应需加以重视。
2)在进行筋腱强度校核时,桩基水平安装误差修正项对校核系数利用比因子UR和相互作用比因子IR的影响显著,尤其对极限工况和自存工况下筋腱强度校核结果的影响更为明显。设计阶段,筋腱强度校核时考虑桩基水平安装误差修正,是一个更为合理、安全的做法。
[1] “典型深水平台概念设计研究”课题组.张力腿平台水动力响应分析[J].中国造船,2005,46(增刊1):477-489.
[2] 余建星,张中华,于皓.张力腿平台总体响应分析方法研究[J].海洋通报,2008,27(2):97-102.
[3] 李飒,李忠刚,韩志强,等.TLP平台锚泊系统和锚固基础的发展状况[J].海洋科学,2009,33(3):80-83.
[4] 董艳秋,胡志敏.张力腿平台及其基础设计[J].海洋工程,2000,18(4):63-68.
[5] 张建红,林小静,鲁晓兵.水平荷载作用下张力腿平台吸力式基础的物理模拟[J].岩土工程学报,2007,29(1):77-81.
[6] 于书铭.张力腿平台整体式负压基础沉贯及抗拔过程数值分析[D].天津:天津大学,2008.
[7] 韦斯俊.浮式结构物系泊系统时域非线性耦合分析[D].哈尔滨:哈尔滨工业大学,2014.
[8] 宋林峰,孙丽萍,赵君龙,钱佳煜.张力腿平台系泊系统敏感性分析[J].中国造船,2012,54(4):109-117.
[9] 于皓,周延东,李欣.张力腿平台的环境载荷及响应[J].中国造船,2007,48(增刊1):336-342.
The Effect of Horizontal Installation Error for TLP Tendon Pile
GAOJing-kun1,WANGYi-jiang1,LIANGYuan-hua2,WEISi-jun2,SUNZheng-ce2
(1.Shenzhen Branch of CNOOC Ltd., Shenzhen Guangdong 518000, China; 2.CCS Ocean Engineering Technology Research and Development Center, Beijing 100007, China)
The TLP motions in designed sea states were simulated and tendon tension time history results were obtained with various pile installation errors to investigate the relation between installation error and tendon tension. The corrections about tendon tension were decided by the relation between installation error and tendon tension. The tendon strength was analyzed by considering the tendon pile installation error corrections. The results showed that it is necessary to consider pile installation corrections when calculating tendon tension in global performance analysis and performing tendon strength analysis.
tension leg platform; tendon pile; installation error; correction
P751
A
1671-7953(2017)05-0090-05
10.3963/j.issn.1671-7953.2017.05.025
2016-11-09
修回日期:2016-11-28
工信部“500 m水深油田生产装备TLP自主研发”专项经费资助
高静坤(1975—),男,硕士,高级工程师
研究方向:海洋结构物设计及工程管理
