随机游走对单陀螺连续旋转寻北影响的分析*

马琛翔, 葛 磊, 王亚凯

(中国航天科工集团第二研究院706所, 北京 100854)

随机游走对单陀螺连续旋转寻北影响的分析*

马琛翔, 葛 磊, 王亚凯

(中国航天科工集团第二研究院706所, 北京 100854)

分析了单陀螺连续旋转寻北方法的原理,指出陀螺的常值漂移可以被积分平滑掉,不影响寻北精度。但陀螺随机游走仍然会影响寻北精度,并推导出了相应误差公式,得出随机游走系数、寻北时间和陀螺寻北仪所处方位都会影响寻北精度的结论,并求出陀螺寻北仪最佳寻北方位和应避免的寻北方位。最后通过三组数值仿真验证了所提出观点的正确性。

陀螺;寻北;旋转;随机游走;精度

0 引言

陀螺寻北仪能够提供北向基准,既可以作为武器瞄准的定向设备,也能为大地测量、石油钻井等民用领域提供精确的方位,因此在国防和民用领域的应用越来越广泛[1]。

传统的陀螺寻北仪采用机械陀螺,精度较高,但是其体积大,结构较为复杂,成本非常昂贵,且不易于保养维护,使用寿命也受到限制,因此,传统陀螺寻北仪逐渐被具有固态陀螺的新型陀螺寻北仪替代[2]。目前,新型陀螺寻北仪由一个陀螺和两个加速度计组成[3-5],也可由3个陀螺和3个加速度计组成[6]。前者能完成载体静态下的寻北;后者即为捷联惯导系统,利用惯性导航初始对准进行寻北。前者结构简单,并且所用惯性器件较少,成本较低,但只能在载体静止不动条件下完成寻北;后者成本较高,但抗干扰性强。出于对成本和应用环境的考虑,目前两种寻北仪在不同领域和应用环境中都被广泛应用。

文中主要对单陀螺寻北进行研究。目前单陀螺寻北仪的寻北方法有两位置寻北、四位置寻北、多位置寻北等[3-5,7],这些方法都是基于旋转定点测量的静态方案,且陀螺本身的零偏和随机漂移对这些方案的影响较大。近年来,有学者提出基于单陀螺连续旋转的寻北方法,该方法与静态寻北方法相比,能更加有效的抑制陀螺零偏和随机漂移,进而提高寻北精度,因此受到众多学者的关注,相关研究成果也不断涌现[8-10]。然而有关陀螺噪声对寻北精度的影响,目前还未有相关文献作理论分析,不利于设计陀螺寻北仪时的精度链的分解,难以从理论上选用合适精度的陀螺,影响了该方法的进一步研究发展。

基于以上原因,文中深入研究了单陀螺连续旋转寻北方法的原理,推导了相应的误差方程,重点分析了陀螺随机游走对寻北精度的影响,并得到相关理论公式,为单陀螺连续旋转寻北仪的工程研制提供理论基础。

1 单陀螺连续旋转寻北原理

通常来说,单陀螺连续旋转寻北仪由一个陀螺和两个加速度计及一个转位构成[8-10],陀螺和加速度计安装在一个平面上,陀螺寻北仪工作时,转位带动陀螺和加速度计以恒定的角速度连续旋转,加速度计的作用为调平,陀螺则用来寻北。

文中为了分析简便,只考虑水平情况,不水平时,可由两个加速度计调平,但还会引入其它误差,在这里不予考虑。

当陀螺安装在水平面上旋转,且不考虑陀螺误差时,陀螺仪的输出为:

ωib(t)=ωiecosLcos(ωt+φ)

其中:ωie为地球自转角速度;L为当地地理纬度;ω为转位转动角速度;φ为寻北仪与北向夹角,是需要求取的量。则陀螺仪在寻北仪上的投影为[10]:

ωis(t)=ωib(t)cos(ωt)=

ωiecosLcos(ωt+φ)cos(ωt)

当陀螺寻北仪以角速度ω匀速旋转了n圈时(n≥1,且为整数),对ωis(t)积分得:

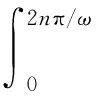
运用三角函数积化和差公式可知:

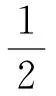
并令T=2nπ/ω,则上面的积分有:

由于A可由陀螺仪输出的各个时刻的角速度在寻北仪上的投影累加求和得到,因此有:

(1)

再对式(1)求反余弦函数,即可得到寻北仪的方位角φ。此即单陀螺连续旋转寻北的原理。

2 误差分析

上面的推导都是在忽略陀螺仪误差的基础上,现在考虑陀螺仪存在误差时的情况。一般来说,影响陀螺性能的主要误差有陀螺零偏和陀螺随机游走(一般用RWC表示),随机游走为陀螺输出白噪声随时间的积分,在陀螺输出角速率时以白噪声的形式体现出来,因此当只考虑陀螺零偏和随机游走这两项误差时,陀螺仪的输出为:

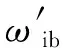
其中:ε(t)为陀螺零偏,且随时间变化而变化,这里为了分析简便,认为ε(t)=ε在整个寻北过程中保持不变;w(t)为0均值、方差为Q的白噪声。

这里需对随机游走的一些性质进行简单介绍。根据随机游走的定义可知[11],随机游走为陀螺输出白噪声随时间的积分,即:

因此,可知随机游走仍然是随机变量,其方差为:

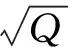
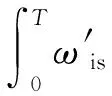
(2)

从上面的式子可以看到,当陀螺旋转n圈时,陀螺零偏被积分平滑掉(前提是认为陀螺零偏不随时间变化),不影响寻北精度,但是,白噪声产生的误差,是不能被平滑掉的,会对寻北结果造成影响。

再考虑上面的白噪声的积分,令:

由于w(t)为白噪声,则B仍然为一随机变量,其均值和方差分别为:

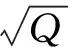
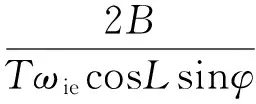
由于B为随机变量,则方位角误差Δφ也是随机变量,其均值为0,方差则为:

则方位角误差Δφ的标准差为:

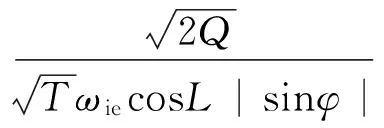
(3)

此即随机游走系数对单陀螺连续旋转寻北影响的误差公式。

从上面的推导中可以发现,当陀螺常值漂移恒定不变时(或短时间内变化较小),经过整圈的积分会被平滑掉,不影响寻北精度,这一点体现出了连续旋转寻北的好处。但是陀螺随机游走系数并不能被积分平滑掉,仍然影响着寻北精度。

从方位角误差公式(3)可以看出,随机游走系数、寻北时间、寻北仪所处方位都影响着寻北结果。随机游走系数越小,则寻北的标准差越小,且与随机游走系数的标准差成正比;寻北时间越长,则寻北的标准差越小,且与寻北时间的1/2次方成反比;同时,寻北仪所处的方位角的正弦的绝对值(|sinφ|)越大,则寻北精度越高,且与|sinφ|成反比,因此,可求出,当φ=90°或270°时,寻北精度最高,而当φ处于0°或180°附近时,寻北精度最差。并且参照上面的式子:

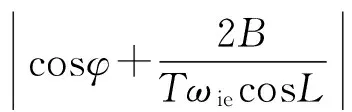
3 仿真分析

本节设计3个仿真试验,以验证所提观点的正确性。

第一个仿真试验是验证单陀螺连续旋转寻北精度与陀螺随机游走系数有关,随机游走系数越小,则寻北精度越高,且与误差公式(3)相吻合;

第二个仿真试验是验证单陀螺连续旋转寻北精度与寻北时间有关,时间越长,精度越高,且与误差公式(3)相吻合;

第三个仿真试验要验证寻北精度与|sinφ|成反比,具体要验证两个内容:1)在方位角0°、180°附近时,寻北精度很差,甚至有出现计算错误而失效的可能;2)方位角在90°、270°附近时,寻北效果最好。

其中,第一组仿真试验列出了10次寻北结果,尽管样本点较少,但是便于分析观察数据分布情况,同时,为了得到较为准确的统计结果,又进行了100次的大样本数据量仿真试验,并列出统计结果。而第二组和第三组试验,限于篇幅,不进行10次寻北仿真试验,只进行100次仿真试验并列出大样本数据统计结果。

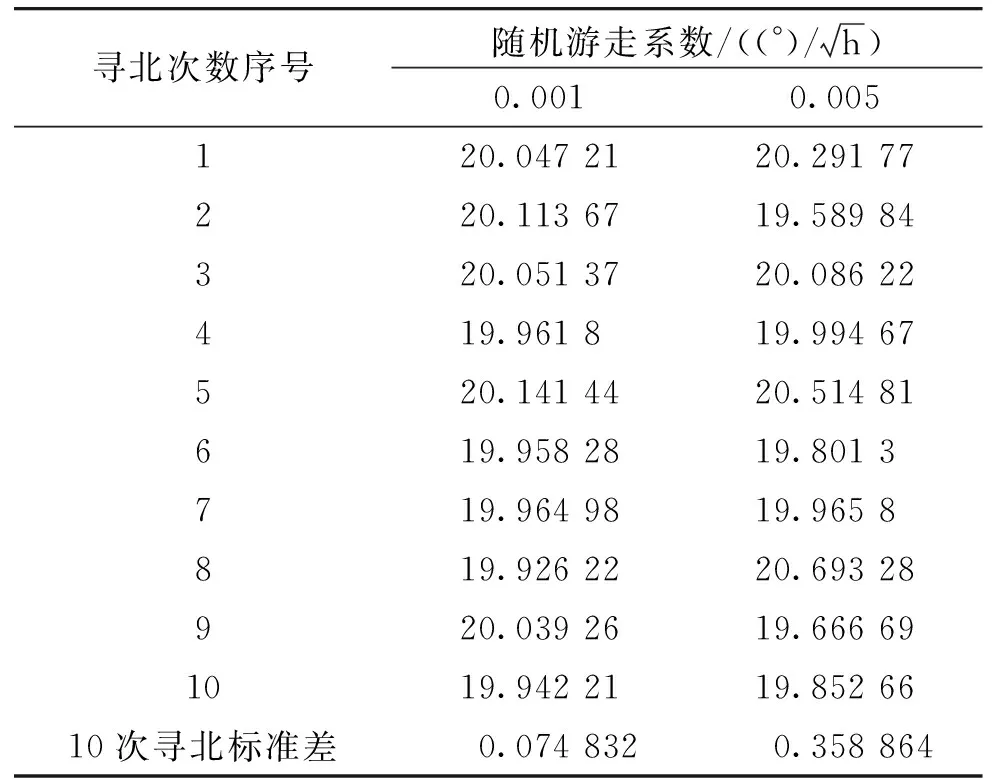
表1 不同随机游走系数寻北精度比较 单位：(°)

从表1中可见,第一组的寻北精度明显优于第二组,第一组的误差标准差约为第二组的1/5,经理论计算,两组试验的标准差为0.070 9°和0.354 7°,与仿真结果吻合较好,但稍有偏差,其原因在于仿真次数太少,样本较少,统计存在偶然性。因此,又做了100次的仿真,其标准差如表2所示。

表2 不同随机游走系数100次仿真标准差与理论值比较

此时可见,寻北结果与理论计算吻合较好。从而验证了第一个结论:单陀螺连续旋转寻北精度与陀螺随机游走系数有关,随机游走系数越小,则寻北精度越高,且与误差公式(3)相吻合。

表3 不同时间100次仿真标准差与理论值比较

从表3可以看出,8 min寻北结果优于4 min寻北结果,且4 min、8 min寻北标准差与理论值吻合程度较高,达到了理论分析的效果。

再设计第三个仿真试验,假设陀螺寻北仪分别处于0°、30°、90°,寻北时间为4 min,其它参数与第二个试验相同,每个方位进行100次仿真。

在仿真中发现,当陀螺寻北仪处于0°时,寻北结果有时会出错,表4列出了寻北出错次数。

表4 陀螺寻北仪0°时寻北错误次数

再观察方位处于30°和90°的寻北情况,其寻北统计结果见表5。从表5可见方位处于90°时的结果明显优于30°。按照理论分析,方位处于90°时的标准差应为30°的一半,从表5中可以看出方位处于90°时寻北统计结果恰好与理论值吻合较好,且前者是后者的二倍,从而验证了误差公式的正确性。

表5 不同方位100次仿真标准差与理论值比较

4 结论

随机游走系数是陀螺的主要误差源之一,也是影响单陀螺寻北精度的重要因素。文中分析了单陀螺连续旋转寻北方法的原理,指出陀螺的常值零偏可以被积分平滑掉,不影响寻北精度,但由于陀螺随机游走系数的存在,导致该方法的寻北精度与随机游走系数、寻北时间和陀螺寻北仪所处方位都有关系,并推导出了相应误差公式。根据公式可知,单陀螺连续旋转寻北方法的寻北精度与陀螺随机游走系数成正比;与寻北时间的1/2次方成反比;与寻北仪所处的方位角的正弦的绝对值(|sinφ|)成反比,并根据误差公式指出,寻北仪方位越接近90°和270°,寻北精度越高,而寻北仪在0°或180°的方位时,寻北精度最差,且可能会计算出错,导致寻北失败,故应当避免寻北仪处在0°或180°的方位时进行寻北。

[1] KIM S J, LEE S S, KWON Y S, et al. Dynamic north-finding scheme based on a fiber optic gyroscope [C]// Proc. SPIE 3087, Navigation and Control Technologies for Unmanned Systems Ⅱ. [S.l.:s.n.],1997: 126-136.

[2] RUFFIN P B. Progress in development of gyroscope for use in tactical weapon system [C]// Proc. SPIE 3990, Smart Structures and Materials 2000: Smart Eletronics and MEMS.[S.l.:s.n.],2000: 2-12.

[3] 姜璐, 于运治, 姜庆国. 二位置光纤陀螺寻北方案及误差分析 [J]. 兵工自动化, 2012, 31(3): 55-57.

[4] 郭喜庆, 黄蕾, 刘伟. 基于光纤陀螺零偏稳定性的高精度寻北方案 [J]. 中国惯性技术学报, 2009, 17(3): 258-260.

[5] 李绪友, 王爽, 张琛. 光纤陀螺寻北仪四位置寻北算法的改进 [J]. 仪器仪表学报, 2009, 30(6): 759-763.

[6] 郝燕玲, 张义, 孙枫, 等. 单轴旋转式捷联惯导方位对准研究 [J]. 仪器仪表学报, 2013, 34(2): 309-315.

[7] 王彬, 翁海娜, 刘畅, 等. 正交检测技术在光纤陀螺寻北仪中的应用 [J]. 中国惯性技术学报, 2013, 21(2): 164-168.

[8] 白云超, 李学琴, 马小辉, 等. 采用旋转调制技术的高精度陀螺寻北方案 [J]. 中国惯性技术学报, 2010, 18(4): 421-424.

[9] 徐海刚, 郭宗本. 一种实用旋转调制式陀螺寻北仪的设计 [J]. 兵工学报, 2010, 31(5): 616-619.

[10] 段苛苛, 李邓化. 光纤陀螺寻北仪连续旋转寻北方案及算法研究 [J]. 仪器仪表学报, 2014, 35(4): 801-806.

[11] 孙国飞, 吴衍记, 那永林. 光纤陀螺中随机游走的分析研究 [J]. 战术导弹技术, 2009(1): 75-78.

AnalysisontheInfluenceofRandomMigrationonSingleGyroContinuousRotaryNorthSeeking

MA Chenxiang, GE Lei, WANG Yakai

(No.706 Institute of the Second Academy, CASIC， Beijing 100854, China)

The principle of the single gyro continuous rotation north seeking method was analyzed in this article to point out that the constant gyro drift could be smoothed out by integral which did not affect the precision of north seeking. But the random migration of gyro would still affect the accuracy of the north seeking. The corresponding error formula was derived and it came to the conclusion that the random migration coefficient, north seeking time and the precision of gyro north seeker would affect north seeking accuracy. The optimal north seeking position of the gyro north seeker and the north seeking position that should be avoided were calculated Finally, the correctness of the proposed view was verified by three groups of numerical simulation.

gyro; north-seeking; rotation; random migration; precision

TN06

A

2016-08-25

马琛翔(1991-),男,山西忻州人,硕士研究生,研究方向:捷联惯导技术。