定向含能动能杆战斗部对TBM毁伤概率分析*

赵永龙, 韩晓明, 陈俊杰

(空军工程大学防空反导学院, 西安 710051)

定向含能动能杆战斗部对TBM毁伤概率分析*

赵永龙, 韩晓明, 陈俊杰

(空军工程大学防空反导学院, 西安 710051)

为准确计算定向含能动能杆战斗部对战术弹道导弹(TBM)的毁伤概率,完成战斗部作战效能评估,文中在分析传统毁伤概率计算方法误差率大、精确率较低的基础上,把动能杆的毁伤能量分为冲击波产生的能量、杆条剩余动能和含能材料化学能,建立基于能量比的毁伤概率计算模型。以假定条件下的M39导弹为TBM目标进行计算,结果验证了模型的合理性与可信性,为毁伤概率计算提供了一种方法和技术手段。

定向含能动能杆战斗部;战术弹道导弹;毁伤概率;能量比

0 引言

定向含能动能杆战斗部是一种新型反战术弹道导弹(TBM)技术,它对TBM目标的毁伤主要是由杆条自身动能和杆条活性材料发生化学反应释放的巨大化学能来实现,其毁伤概率对于评估导弹作战效能具有重要作用。由于TBM的特殊性,如机动能力快、突防能力强等特点使得原先的一些计算毁伤概率的经验公式并不能很好反映出战斗部对TBM的综合毁伤概率。

常见计算方法主要有两种:①计算单枚破片引爆装药的概率。假定在理想的状态下,单枚即可引爆装药。由于TBM装药的稳定性,需由多个破片对装药的累积冲击作用下才能到达装药的引爆阈值,从而引爆装药。因此这种计算毁伤概率的方法没有考虑实际的毁伤环境,并不适用于杆条对TBM毁伤概率的计算。②利用穿透目标的破片数或杆条数Nn(有效杆条数)与能够接触到目标壳体表面的破片或杆条总数Nm的比值作为破片或者杆条对目标的毁伤概率,即毁伤概率P=Nn/Nm。由于TBM的壳体厚度相比其他目标要厚得多,有一部分穿透的破片或杆条很有可能在穿透过程中剩余速度衰减为零,这些数目的破片或杆条并没有真正对TBM内的部件造成毁伤。因此该计算毁伤概率的方法也不适用于杆条对TBM的毁伤概率的计算。基于此,文中将动能杆条毁伤能量分为冲击波产生的能量、杆条剩余动能和含能材料化学能,提出基于能量比的毁伤概率计算方法。

1 基于能量比的战斗部毁伤概率计算方法

定向含能动能杆最终对TBM的主要毁伤因子有两个:动能杆条和杆条内的含能材料。能量比的概念在于利用进入TBM目标内的动能杆条数的所有能量与能够接触到TBM目标表面的杆条数的总能量的比值作为定向含能动能杆对TBM毁伤概率。进入目标内的杆条的所有能量包括3种:杆条与TBM壳体切割作用下产生的冲击波的能量、剩余杆条的总动能和含能材料释放的能量。这种方法能够较好解决传统毁伤概率计算方法的误差率大、精确率较低等不足之处,适用于含能材料释放出的能量不大于接触到TBM目标表面的杆条数的总能量。

基于能量比的定向含能动能杆对TBM毁伤概率P的公式为:

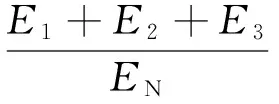
(1)

式中:E1为冲击波产生的能量;E2为含能材料发生反应产生的爆轰能量;E3为进入TBM目标内的杆条的剩余动能;EN为打上TBM目标表面的杆条的总能量。

接触到TBM目标表面的杆条的总能量为杆条动能EN:

(2)

式中:mB表示能够接触TBM目标上的杆条的质量;VB表示能够接触到TBM目标上的杆条的速度。

2 毁伤概率计算模型

2.1 战斗部冲击波对目标的毁伤概率计算模型

冲击波对目标的有效杀伤距离D可以用下式表示[1]:

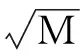
(3)

式中:KT为目标易损性系数,一般取0.3～0.5;M为等效TNT裸装药量(kg)。

TBM被战斗部杀伤的评判标准为:冲击波的有效杀伤距离D大于炸点与TBM的壳体的最小距离d[1],即:

d≤D

(4)

2.2 基于经验公式的杆条洞穿概率计算模型

1)杆条穿靶的极限速度计算

杆条穿孔速度Vc的判据由经验公式[2]确定:

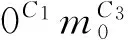
(5)

式中:Af为杆条碰靶时的迎风面积(m2);m0为杆条的质量(kg);θR为杆条着角(°);h为靶板厚度(m);C1、C2、C3、C4为与目标材料相关的无量纲系数。

杆条平均迎风面积计算的经验公式[3]为:

(6)

式中:k为杆条形状系数。

2)杆条击穿TBM目标壳体概率计算

杆条对TBM壳体洞穿的概率通常以杆条击穿TBM壳体的比动能ER来衡量,杆条的比动能为:

(7)

式中:VR为杆条着靶速度(m/s);h′为TBM壳体材料等效硬铝靶板的厚度[4](m)。

杆条击穿TBM壳体的概率[4]为:

(8)

3)有效杆条个数计算

目前,判定有效杆条数的标准主要有3种:极限速度标准、动能标准、侵彻深度标准。文中选取极限速度标准来确定有效杆条数。

参考弹目交会参数,根据式(5)求得杆条的极限穿透速度和杆条与TBM相遇时的速度进行对比,判断准则如下:

(9)

2.3 普通破片(杆条)引爆炸药的概率计算模型

战斗部引爆作用的机理[5]主要是毁伤元素冲击目标弹药舱内的装药,并将其引爆。装药参数、冲击体参数和冲击体与装药的遭遇条件都会对引爆装药产生重要的影响。

对于TBM而言,引爆作用的过程首先是杆条击穿TBM弹药舱,然后才能接触装药,则单枚杆条造成引爆弹药舱的概率由下述经验公式[4]计算:

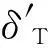
2.4 定向含能动能杆击爆装药毁伤概率计算模型

关于战斗部击爆装药的过程,蒋建伟[6]认为从定性的看,当冲击压力比较低而变形和变形速率较大时,以宏观剪切机制为主;当冲击压力较高而变形较小时,以冲击起爆机理为主。定向含能动能杆在侵彻靶板时相对速度高,给靶板造成的冲击压力相对普通杀伤破片较大,且杆条变形率低,宏观剪切作用可以忽略不计,引爆战斗部内装药主要以冲击起爆机理为主。

1)冲击波引爆炸药过程

动能杆以速度VR高速撞击TBM弹体,碰撞后产生两个冲击波:一种以速度VS2传入杆条中,另一种以波速VS1传入TBM壳体中。依据冲击接口上物质是连续的原理[6],动能杆撞击壳体前杆条上各个质点的速度是相同的。

TBM屏蔽炸药的屏蔽板较薄,可忽略应力波强度在靶板内的衰减,则应力的冲击波透过屏蔽板到达与炸药相接触的界面时产生透射波的波速Vt与冲击波的波速VS1相同。

根据介质连续条件及动量守恒定理[7],则有:

ρc(C3+S3V3)V3=

ρa[C1+S1(2VS1-V3)](2VS1-V3)

(12)

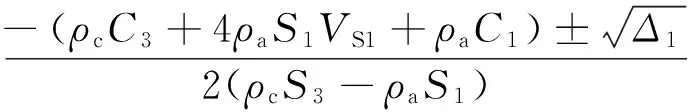
(13)

式中:Δ1=(ρcC3+4ρaS1VS1+ρaC1)2-4(ρcS3-ρaS1)·(2ρaC1VS1+4ρaS1VS12),ρa为TBM壳体材料密度(kg/m3);ρb为杆条材料密度(kg/m3);ρc为TBM炸药的密度(kg·s2/m4);V3为冲击波进入炸药内的速度(m/s);C、S为不同物质的冲击参数。

冲击波对TBM炸药的作用强度:

P3=ρc(C3+S3V3)V3

(14)

冲击波对TBM炸药的作用时间t可依据文献[8]来判定,具体的判定公式[8]为:

(15)

冲击波产生的总能量为:

E1=P3V3t

(16)

2)定向含能动能杆击爆炸药毁伤概率计算模型

定向含能动能杆对带壳炸药起爆过程的微观机制可以分为如下3种:第一是动能杆条在高速侵彻条件下形成的冲击波在炸药内产生热点从而引爆炸药;第二是动能杆内的含能材料发生反应和爆炸释放出大量的热量或者由爆炸产生强烈的爆轰引爆炸药;第三是剩余侵彻体(杆条)直接引爆炸药。文中设定动能杆内的含能材料全部发生反应,则考虑前两种的起爆过程。

设冲击波产生的能量为E1,含能材料发生反应产生的爆轰能量为E2,杆条的剩余动能为E3,则进入TBM内的含能动能杆条的总能量为:

E总=E1+E2+E3

(17)

杆条的剩余动能E3为:

(18)

式中:mr为杆条进入TBM目标内的剩余质量;Vr为杆条进入TBM目标内的剩余速度。

进入TBM内部的定向含能动能杆击爆炸药毁伤概率以起爆能量为计算准则,具体公式为:

(19)

3 算例验证

1)原始数据

以M39导弹为TBM目标,定向含能动能杆战斗部设定杆条沿轴向飞散角为60°,径向飞散角为160°,战斗部的有效杀伤半径为25 m,杆条以一定的规则排列,总数为400枚,每个杆条的长度为0.12 m,直径为0.004 m,质量为0.015 kg,靶板厚度为0.006 m,杆条材料和M39导弹采用是钢质材料,目标材料相关系数C1、C2、C3、C4分别为6.601,0.906,-0.963,-0.359,材料的冲击参数C和S选取文献[9]给出的数值。文中选取的含能材料采用MAT_HIGH_EXPLOS工VE_BURN材料模型[10]。该含能材料的密度为1 687.1 kg/m3,爆轰速度为7.45 km/s,爆轰压力为22.0 GPa,爆轰能量为35.84 J/g。每个动能杆中包含10g的含能材料,M39导弹的内置炸药选取Comp B(RDX60/TNT40),起爆阈值为122 J/cm2。在弹目交会时,杆条的初速度设定为300 m/s,防空反导导弹的速度设为1 000 m/s,战术弹道导弹(M39)的再入弹头速度为1 500 m/s,设定交会角为0°。

2)计算结果与分析

经仿真计算得出的结果为:在400枚动能杆条中,能够接触到TBM目标的有300枚杆条,每个杆条与目标有不同着角和攻角,根据式(5)和式(9)计算可得,能够洞穿目标壳体的杆条数目为229个。

(a)不考虑含能材料时,动能杆对TBM目标的毁伤概率(击爆炸药)

冲击波能与杆条动能由式(16)和式(18)可得:E1+E3=2.115 6×106J。

能够接触到TBM目标上的动能杆杆条数的总能量由式(2)可得:EN=2.795 3×106J。

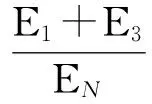
(b)考虑含能材料时,动能杆对TBM目标的毁伤概率(击爆炸药)

M39导弹的内置炸药为CompB(RDX60/TNT40),其起爆阈值为122J/cm2;设杆条作用在TBM再入弹头炸药横截面为1.5m2,则引爆TBM装药的起爆阈值:E起爆阈值=2.196×106J。

接触到TBM目标上的含能动能杆的总能量为:EN=2.795 3×106J。

含能材料反应所产生的爆轰能为:E2=82 330.08J。

考虑含能材料时,进入TBM目标内含能动能杆所产生的总能量为:E总=2.198×106J。

4 结论

由以上计算结果可知:E总>E起爆阈值,E1+E3

文中针对定向含能动能杆战斗部毁伤概率计算的重要意义,在分析传统计算方法缺陷的基础上,建立基于能量比的计算模型,计算结果证明了模型的可信性。论文研究成果为计算定向含能动能杆战斗部毁伤概率提供了一种新的方法与技术手段,同时对于计算其他类型的战斗部毁伤概率也具有重要参考价值。

[1] 牛冰, 谷良贤, 龚春林. 破片战斗部对武装直升机目标的威力评估 [J]. 弹道学报, 2011, 23(1): 68-71.

[2] 许寄阳. 杆条战斗部对固定翼飞机的毁伤效能研究 [D]. 南京: 南京理工大学, 2009: 36-37.

[3] 李向东, 张运法, 魏惠之. AHEAD弹对导弹目标的毁伤研究 [J]. 兵工学报, 2001, 22(4): 556-559.

[4] 白梅, 张茂林, 张锡恩. 破片杀伤型战斗部对装备损伤的建模与仿真 [J]. 计算机仿真, 2005, 22(1): 40-42.

[5] 任磊. 飞机致命性部件毁伤概率计算方法研究 [D]. 西安: 西北工业大学, 2006: 19-20.

[6] 蒋建伟, 卢永刚, 钱立新. 射击迹线技术在战斗部破片场仿真中的应用 [J]. 弹箭与制导学报, 2001, 21(1): 29-34.

[7] 许化珍. 含能破片对柴油箱的引燃机理 [D]. 南京: 南京理工大学, 2012: 14-15.

[8] 章冠人, 陈大年. 凝聚炸药起爆动力学 [M]. 北京: 国防工业出版社, 1991: 57-63.

[9] 董小瑞, 隋树元. 破片对屏蔽炸药的撞击起爆研究 [J]. 华北工学院学报, 1999, 20(3): 236-238.

[10] 李旭峰. 含能破片对模拟战斗部的引爆机理研究 [D]. 南京: 南京理工大学, 2006: 22-23.

AnalysisofTheDamageProbabilityofDirectionalEnergeticKE-rodWarheadtoTBM

ZHAO Yonglong, HAN Xiaoming, CHEN Junjie

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

In order to accurately calculate the damage probability of directional energetic KE-rod warhead to tactical ballistic missile (TBM) and complete combat effectiveness evaluation of warhead, on the basis of the analysis of the big error rate and low accuracy of traditional damage probability calculation method, the damage energy of the kinetic rod was divided into the energy generated by the shock wave, residual kinetic energy of rod and the chemical energy of energetic material, and the damage probability calculation model based on energy ratio was established. Under the assumption, the paper choosed M39 missile as TBM target to calculate damage probability. The results verified the rationality and credibility of the model, and it provided a method and technical means for damage probability calculation.

directional energetic KE-rod warhead; tactical ballistic missile; damage probability; energy ratio

TJ760.3

A

2016-07-11

赵永龙(1991-),男,四川绵阳人,硕士研究生,研究方向:装备管理理论与方法。