旋转弹舵机控制滞后及其对策研究*

陈利风, 李 龙, 姚晓先

(1 江苏自动化研究所, 江苏连云港 222006; 2 北京理工大学, 北京 100081)

旋转弹舵机控制滞后及其对策研究*

陈利风1, 李 龙1, 姚晓先2

(1 江苏自动化研究所, 江苏连云港 222006; 2 北京理工大学, 北京 100081)

针对旋转弹飞行过程中舵机控制滞后的难点,建立了控制滞后角的分析模型,重点研究了舵机、地磁陀螺和弹载计算机三方面导致滞后角的因素,给出了控制总滞后角计算方法。基于滞后与时间延迟的线性关系,提出了按滚转角速率补偿滞后角的算法,并进行了实验验证,实验结果表明其较好的解决了舵机控制滞后的问题,具有较高的工程应用价值。

旋转弹;控制滞后;滞后角;对策

0 引言

旋转弹在飞行过程中以变化的角速度绕纵轴旋转,通常采用两对互相垂直的鸭舵来控制弹的俯仰和偏航通道,研究表明这种双通道的鸭舵控制方式比常规尾翼控制具有更好的稳定性和更高的控制效率[1],弹体结构如图1。

旋转弹的控制滞后指的是针对当前时刻旋转弹的状态舵机实际形成的控制力比理想的控制要滞后。在实际的控制过程中,滞后角随转速增大而增大,如果控制不合理,就会导致俯仰和偏航通道间存在变化的大耦合,反应到弹道坐标上的现象是:本来是控制高度,结果是高度控制效果较弱甚至没有,相反偏航控制效果明显[2]。

舵机滞后补偿是旋转弹控制系统的一个难点,在一些文献上,如陈罗婧、毕彦超等人将舵机视为一阶惯性环节,计算了舵机滞后对控制系统的影响,并通过指令补偿和设计自动驾驶仪来解决舵机滞后带来的问题[3-4]。莫波根据旋转火箭弹的控制过程的数学模型,分析了火箭弹的对称控制的特性[5]。这些文献都缺乏系统提出舵机控制滞后分析方法及解决措施,文中结合工程实际,通过建立旋转弹控制指令分解模型,给出了求解舵机滞后角的方法,分析了影响控制滞后的因素,最后给出了按转速补偿滞后角的算法,并在试验中进行了验证。

1 控制滞后角分析

1.1 控制指令分解模型

首先定义固定在弹体上的弹体坐标系为o-x1y1z1。旋转弹的1号舵和3号舵固定在y1轴上,给定控制指令为正时,产生正的控制力Fzc;2号舵和4号舵固定在z1轴上,给定控制指令为正时,产生正的控制力Fyc。再定义准弹体坐标系o-xyz,y轴始终竖直向上,z轴始终水平,其中Fciy为旋转弹在竖直方向上受到的合力,Fciz为水平方向上受到的合力,γ为弹体坐标系与准弹体坐标系之间的夹角。弹体坐标系与准弹体坐标系之间的关系如图2所示。

假设当前时刻弹体旋转到图2位置,1号和3号舵的控制指令为δz,2号和4号舵的控制指令为δy,分别在弹体坐标系中形成控制力Fzc和Fyc为:

(1)

将弹体坐标系中的控制力转换到准弹体坐标系中,有:

(2)

对弹旋一周的舵偏角积分求得竖直和水平方向等效控制力及其与y轴正向的夹角θi为:

(3)

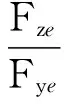
(4)

将式(1)～式(3)代入式(4)得:

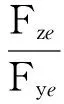
(5)

可以看出理想控制力的方向只与两对舵的等效舵偏角指令有关。

1.2 外弹道实测控制力方向模型

旋转弹在飞行中受重力(G)、推力(P)、气动力(N)和控制力(Fcr)的作用,即:

F=G+P+N+Fcr

(6)

将合力(F)分解到竖直方向和水平方向得:

(7)

式中：Fy和Fz,采用多项式拟合实测的外弹道在地面坐标系中的y轴和z轴的数据来求取,多项式如下:

(8)

式中:a0,a1,a2,…,an∈R;b0,b1,b2,…,bn∈R;t为时间。分别对多项式二次求导,得:

(9)

式中：ay和az分别为外弹道飞行中在竖直和水平方向的合加速度。则外弹道飞行中在竖直和水平方向的合力分别为:

(10)

则控制力竖直分量(Fcry)和水平分量(Fcrz)的大小和实际控制力与竖直方向的夹角(θr)为:

(11)

(12)

式中：Py、Pz、Ny、Nz分别为推力和气动力在竖直和水平方向的分量,其值可以通过原始数据获取。acry和acrz为控制力产生的竖直和水平方向的加速度。从式(13)可以看出实际控制力的方向可以通过对应的加速度来求得。

1.3 控制滞后角模型

旋转弹在飞行过程中的总滞后角为Δθ,如图3所示。

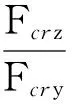
(13)

Δθ大于零表示实际控制力方向滞后于理论控制力方向,小于零表示实际控制力方向超前于理论控制力方向。

在o-yz直角坐标系中,首先以俯仰方向等效舵偏角指令δye和偏航方向等效舵偏角指令δze分别为等效舵偏角指令点的y轴和z轴的坐标,依时间先后实线连接一段时间内的等效舵偏角指令点,然后以控制力产生的竖直方向的加速度acry和水平方向的加速度acrz分别为控制加速度点的y轴和z轴坐标,依时间先后虚线连接相同时间内的控制加速度点。对比两条线在直角坐标系中的方向即可判断滞后角。

从图4中看出,实线的方向在y轴正向附近,虚线方向在z轴正向附近,从前往后看弹旋方向为顺时针,可见实线的方向明显滞后于虚线的方向。蓝色实线都集中在一点表示这段时间内等效舵偏角指令的方向不变,红色虚线的方向缓慢变化是由于在执行指令形成加速度的过程中存在误差以及在弹道拟合过程中也存在误差。

2 滞后角影响因素分析

系统迟滞总是存在于各个组件中[6]。旋转弹系统包括:弹载计算机、舵机、地磁陀螺、GPS和高度计等。因为导致控制滞后的因素肯定在控制流程中,故分析其控制流程,发现造成控制滞后角的3个因素为:舵机滞后、地磁陀螺滞后和弹载计算机滞后。以下分别分析滞后角的影响因素及大小。

2.1 舵机滞后

假设舵机为一阶惯性环节,其数学模型为:

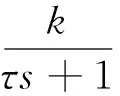
(14)

在弹体坐标系下有:

(15)

式中:δyc、δzc为输入舵机的舵偏角指令;δy、δz为舵机响应的实际偏转角度。从上面的模型看出舵机存在滞后,且滞后角随旋转频率的变化而变化。假设要形成竖直向上的等效舵偏角大小为A的力,令两对舵机输入信号为式(16),则输出信号为式(17)。

(16)

(17)

式中：φ(ωx,M)表示弹旋频率为ωx且舵偏角幅值为M时舵机的相角滞后。

计算出理论等效舵偏角如式(18),实际等效舵偏角如式(19)。

(18)

(19)

则理论等效舵偏角和实际等效舵偏角的方向差值即舵机滞后角为:φ=φ(ωx,M)。分析发现是由于转速ωx和舵偏角幅值M变化导致φ的变化,它们的关系曲线如图5。

2.2 地磁陀螺滞后

地磁陀螺测量旋转弹的滚转角,为舵片正弦运动提供时间基准。其在测量滚转角的过程中存在滞后,地磁陀螺产生滞后角存在三方面的原因,即:数据处理滞后,地磁陀螺测角非理想,零点误差。后面将依次分析。

1)数据处理滞后

地磁陀螺生成数据的时序如图6,时刻1传感器采集数据,时刻1到时刻2之间进行数据处理,耗时Ams,并在时刻2向弹载计算机发送数据,于时刻3数据发送完毕,耗时Bms。在数据处理和发送(A+B) ms中,弹体已经旋转了一定的角度,故在此时舵片产生的控制力的方向滞后于采集数据时刻的控制力(即理想控制力)的方向,滞后角的大小为:

Δθd=0.36ωx(A+B)

(20)

式中ωx为转速(r/s)。

2)地磁陀螺测角非理想

在理想情况下,旋转弹的自选频率是固定的,在每个旋转周期内地磁陀螺测角应该是从0°到360°线性变化的,然而实际采集的地磁陀螺变化曲线为非理想的,部分采集数据如图7。

通过对比使用非理想滚转角数据生成的指令与理想滚转角数据生成的指令的方向,可以求出两个方向的夹角。根据非理想滚转角数据生成的等效舵偏角指令方向与理想滚转角数据生成的等效舵偏角指令方向如图8,弹旋方向在图中为顺时针,显然非理想滚转角数据生成的等效舵偏角指令滞后于理想滚转角数据生成的等效舵偏角指令,滞后角大小为Δθl,与地磁陀螺实际测角有关。

3)零点误差

在地磁陀螺正确装定情况下,地磁陀螺测量滚转角零点滞后于绝对零点Δγ,如图9。弹载计算机是根据地磁陀螺测量的滚转角来给定控制指令方向的,如果地磁陀螺测量的零点滞后Δγ,则控制指令滞后Δγ,相应的舵机产生的控制力滞后Δγ。

2.3 弹载计算机滞后

在飞行过程中,弹载设备测量旋转弹的飞行要素,然后将飞行要素发送到弹载计算机,弹载计算机根据飞行要素计算出控制指令并将指令发送给舵机系统执行。弹载计算机生成指令的时序如图10,时刻1接收飞行要素数据,时刻1到时刻2之间根据数据生成控制指令,耗时Cms,并在时刻2向舵机系统发送控制指令,于时刻3数据发送完毕,耗时Dms。在指令生成和发送(C+D) ms中,弹体已经旋转了一定的角度,故在此时发送给舵机控制指令的方向滞后于接收飞行要素时应该产生控制指令的方向,滞后角的大小为:

Δθc=0.36ωx(C+D)

(21)

2.4 实例分析

分析得到舵机滞后角是由于舵机系统在执行控制指令的过程中存在滞后,地磁陀螺滞后角是由于地磁陀螺在测量滚转角的过程中存在数据处理滞后、地磁陀螺测角非理想以及零点误差,弹载计算机滞后角是由于其计算控制指令和发送指令这段时间导致滞后。且以上滞后角的大小均与滞后时间和转速有关。假设旋转弹转速为10 r/s,舵偏角幅值为4°,根据控制滞后角模型计算得总滞后角Δθ范围为:86°～97°。其中舵机滞后角为φ=22°;假设地磁陀螺零点误差Δγ=5°,地磁陀螺滞后角为Δθg=Δθd+Δθl+Δγ=3.6°(A+B)+23°+5°,当A=4 ms、B=0.5 ms时,Δθg=44.2°;弹载计算机滞后角为Δθc=3.6°(C+D),当C=4 ms、D=1 ms时,Δθc=18°。分析的各滞后角示意如图11,其中三部分滞后角加起来共Δθa=22°+44.2°+18°=84.2°,可见Δθa与Δθ的值大小相差不大,可见文中分析出了绝大部分产生滞后角的因素,其余部分差值可能是由于采样误差和弹道拟合过程的误差造成的。后续根据分析的情况给出解决滞后的方法。

3 对策及验证

现有的处理滞后角的方法主要有两种,一种方法是减小滞后角,即通过提升舵机性能,地磁陀螺的数据处理速度和精度,以及弹载计算机的处理速度,由于滞后影响因素都是旋转弹固有的特征,通过这种方法只能减小滞后角的影响,不能消除。另一种方法是补偿滞后角,即在形成指令的时候,在测量得到滚转角的基础上再按转速加上补偿角Δθa(ωx),补偿角包括所有滞后时间按转速转换成的滞后角以及测量误差造成的滞后角,这样能够完全消除滞后角的影响,下面介绍滞后角补偿的方法。

实际计算的角度为γ=γm+Δθa(ωx)。当旋转弹在飞行过程中需要舵偏幅值为M形成的竖直向上的力的时候,两对舵机输入指令为:

(22)

则形成的俯仰和偏航方向等效舵偏角指令为:

(23)

其等效舵偏角指令形成的控制力方向与y轴正向的夹角为:

(24)

为了验证对策的正确性,完成了如下实验。为了使得旋转弹形成大小为M竖直向上的力,分别实验了在形成控制指令时不加入补偿角和加入补偿角两种情况。实验过程中为了清晰观察加补偿角是否有用,使用高速相机(3 000帧/s)拍摄旋转状态下旋转弹的舵偏角情况。不加入补偿角和加入补偿角的舵偏状态对比如图13。

理想情况下在每次旋转经过竖直方向时舵偏角应该是0°,这样才能形成竖直向上的力,如果在每次旋转经过竖直方向后舵偏角才为0°,则存在滞后。图13中红色箭头指向的灰线为通过垂吊重物形成的竖直方向基准,可以看见不加入补偿角时舵偏角在过竖直方向后一个角度才为0°, 其存在一定滞后,

形成的控制力方向为图中1号舵的指向,与理想控制力方向相差较大。在加入补偿角后舵偏角在竖直方向附近为0°,虽然其存在较小的误差,但是形成的控制力方向接近理想的控制力方向,不会影响控制效果,可见以上的对策是有效的。

4 结论

旋转弹的控制滞后即实际形成的控制力方向滞后于理想的控制力,这在控制过程中是一个严重的问题,其形成的控制力方向错误,导致竖直方向的力不能控制高度,侧方向的力不能控制偏航,控制状态混乱。仔细分析控制滞后的特点,发现导致控制滞后的三个方面主要是舵机、地磁陀螺和弹载计算机。通过试验和计算分析,发现主要是由于舵机控制过程慢和机械结构误差、地磁陀螺信号采集和处理滞后、弹载计算机计算滞后造成的,并且建立模型,求得各部分滞后角的大小。根据分析结果,提出滞后补偿的解决方法,即在形成控制指令的时候,在测量得到滚转角的基础上加补偿角,形成超前的指令,从而使得实际形成的控制力方向超前,形成准确的控制力,实验表明其较好的解决了控制滞后的问题。

滞后补偿的方法本质上是通过超前形成指令来解决滞后的问题。在所有的实际控制系统中都存在或多或少的控制滞后,这些控制滞后会不同程度的扰乱控制过程,可采用文中所说的滞后补偿方法,针对不同的系统分析产生滞后的因素,补偿不同的滞后值,从而达到满意的控制效果。

[1] WERNERT Philippe, THEODOULS Spilios, MOREL Yannick. Flight dynamics properties of 155 mm spin-stabilized projectiles analyzed in different body frames: AIAA 2010-7640 [R]. [S.l.:s.n.],2010.

[2] FORTESCUE P W. Pitch/Yaw coupling due to roll of an axisymmetric missile with autopilot [J]. Aeronautical Ouarterly, 1982，33(2): 124-139.

[3] CHEN Luo-jing, LIU Li, YU Jian-qiao. Transform and coupling analysis of double-channel control rolling missile autopilot loop [J]. Transactions of Bejing Institute of Technology, 2007, 27(10): 847-850.

[4] 毕艳超，姚晓先，宋晓东，等. 双通道控制旋转导弹的舵机控制研究 [J]. 弹箭与制导学报，2014, 34(2): 25-28.

[5] Mo bo, GAO En-yu, YANG Shu-xing. Research on Spin Rocket Double-channel Proportional Control Characteristics [C]//Proceedings of Second International Conference on Innovative Couputing, Information and Control.New York: IEEE, 2007.

[6] HARTREED R, PORTER A, CALLENDER A, et al. Time-lag in a control system:II [C]// Proceeding of the Royal Society of London: Series A Mathematical and Physical Sciences. London: The Royal Seciety, 1937, 161(907): 460-476.

StudyonSteeringEngineControlHysteresisandtheCountermeasureofSpinningMissile

CHEN Lifeng1, LI Long1, YAO Xiaoxian2

(1 Jiangsu Automation Reserch Institution, Jiangsu Lianyungang 222006, China; 2 Beijing Institute of Technology, Beijing 100081, China)

Aiming at the difficulty of the steering engine control hysteresis in the flight process of spinning projectile, a calculation method for controlling the total lagging angle was established by establishing an analysis model and the research on three components leading to lagging angle, which were steering engine, geomagnetic gyro and missile-borne computer. At last, the algorithm of compensating lagging angle according to the rate of roll angle was proposed and tested based on the linear relationship between hysteresis and time delay. The results showed that this method effectively solved the steering engine control hysteresis problem, and had high engineering application value.

spinning missile; control hysteresis; lagging angle; countermeasure

TJ765.2

A

2016-10-19

陈利风(1977-),男,湖北黄梅人,高级工程师,硕士,研究方向:武器装备试验。