空天飞行器高超声速气动热特性计算方法

王 鹏, 房 帅, 金 鑫, 张卫民

(中国航天空气动力技术研究院, 北京 100074)

空天飞行器高超声速气动热特性计算方法

王 鹏*, 房 帅, 金 鑫, 张卫民

(中国航天空气动力技术研究院, 北京 100074)

通过数值方法和基于无粘表面流线的工程快速方法，计算了空天飞行器基本型在Ma=8.0及Ma=10.2状态下的气动热特性。数值方法计算格式选用Roe的FDS格式，工程快速方法中飞行器的表面流线是通过基于直角网格的无粘Euler方程计算得到的，采用参考焓理论沿流线积分即得到沿流线的表面热流分布。结果表明，本文建立的气动热工程方法及数值方法得到的机身及机翼的热流分布与试验数据吻合较好，得到的驻点热流值与试验数据的误差小于5%。

表面流线；气动热；空天飞行器；数值计算；工程方法

0 引 言

以往的飞行器设计中，飞行器的热环境主要依靠试验来确定，费用高昂，设计成本高，还存在地面数据往飞行状态外推的问题，且难于分析流场细节[1-2]。随着计算流体力学的发展，利用CFD技术结合风洞试验来预测气动加热是飞行器设计的重要发展方向。但高超声速气动热的数值模拟受数值格式、网格生成、收敛问题[3-6]等各方面因素的影响,多种因素之间的交错影响决定了数值计算热流的复杂性。为了适应高超声速飞行器概念研究和设计需要,在发展高精度的CFD技术的同时，寻求一种快速、简便、精度较高的气动热工程方法具有重要意义。

基于无粘表面流线的气动热计算方法是求解高超声速钝头体飞行器表面热流的有效工程方法。它的计算效率很高，对于简单的钝头体外形，精确度也有保证，在高超声速钝头体飞行器研制初期，发挥着较大作用。由DeJarnette和Hamiton[7]开发的基于轴对称比拟的方法生成表面流线，沿流线积分得到热流分布。流线求解方法有跟踪流线法和几何流线法，但两种求解方法差别较大，且对于有翼面的复杂外形很难求解。随后DeJarnette等[8]开发了UNLAUCH系列程序，逐步将该方法用于较复杂外形。但这类方法的缺陷是流线会间断，从而影响热流的连续求解(作者后续研究逐渐解决了该问题)。

国内研究人员对基于表面流线的方法进行过研究[9]，对于简单的钝头体进行过较为详细的验证，但并没有与数值计算及风洞试验进行过系统地比较；且对于具有翼面的较复杂的外形，由于存在流线间断等原因，未有研究人员进行过系统验证。

为此，本文建立了一种新的无粘表面流线求解方法，采用基于直角网格的无粘Euler方程计算得到飞行器表面流线，根据Eckert参考焓理论沿流线积分确定热流，并与数值计算与风洞试验结果进行了系统地比较。

1 计算模型

本文研究的空天飞行器基本型选自李素循主编的《典型外形高超声速流动特性》一书[10]，是一种无立尾、机身与三角翼融合的气动布局。

该空天飞行器外形及热流测点分布如图1所示。

位于机身上的热流测点分布为：热流测点1-12位于纵向对称面的上表面，测点13为驻点热流测点，14-40位于纵向对称面的下表面。图1(c)为位于机翼的两个横截面上的热流测点分布。风洞试验在JF48脉冲型风洞中进行，详见文献[10]。

2 工程快速计算理论

2.1基于直角网格的无粘欧拉方程计算理论

计算的流场区域取为大的长方体, 图2为计算的直角网格。为了在物面附近加密网格，找出与物面相碰的单元，这里不仅将相碰的单元等分为8个单元， 而且将其邻居以及邻居的邻居等等也划分为8个,如此形成第2层加密网格。再对第2层网格做上述自适应加密, 形成第3层加密网格。继续上述过程, 可以形成近壁面的多层加密网格。

采用Jameson 的有限体积法, 将积分型Euler方程应用到任一单元, 得到

式中，Wk为守恒变量在单元中的平均值, 或格心处的值；Fi是单元表面的通量张量，可取相邻单元处通量的平均值；Si为表面有效面积；Ωk为单元体积。求和是对单元的m个表面进行。在远场边界采用无反射边界条件。Dk为附加的耗散项， 取二阶与四阶耗散的融合。

2.2表面流线生成方法

基于上述计算理论，考虑某一时刻t的速度场，在飞行器表面取任一点P0(x,y,z,t)，首先找到与该点最近的物面法向第一层的网格编号C0，将网格C0格心P1存储的速度V(x,y,z)作为下游流线上P1点的切线方向，并取该网格步长dh作为流线的积分步长。在距离P1(x,y,z,t)点V(x,y,z)*dh范围内寻找一与C0邻近网格格心点P2(x,y,z,t)，若P2(x,y,z,t)与P1(x,y,z,t)坐标向量与P1点的速度矢量形成的夹角最小且不大于60°(若无满足条件的点则作为流线的终点)，则将P2点作为下游流线的第二点，以此类推求出下游流线上的各点，得到一条折线，记为经过飞行器表面P0点的流线；P0点上游流线求法类似。图3为利用本文建立的方法得到的空天飞行器的表面无粘流线示意图。

2.3热流计算方法

2.3.1 驻点热流计算方法

工程设计中驻点热流计算理论较多，主要有Fay-Riddell、Kemp-Riddell及Lees等公式[11-12]。Fay-Riddell理论利用相似性假定和多罗得尼津-曼格勒变换，将高温气体边界层偏微分方程转化为常微分方程，将气体热力学特性等有关的无因次参数假设为一系列常数，利用萨瑟兰定律，得出的驻点热流经验公式。本文驻点热流计算采用的就是Fay-Riddell公式。平衡边界层条件下的驻点热流计算公式为：

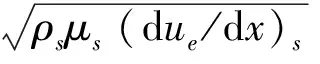
(2)

其中，hD为空气平均离解焓，Pr为普朗特数，Le为路易斯数，h∞为来流焓值，hs为驻点焓值，μs为驻点粘性系数，ρs为驻点密度，ζ为壁面焓值与驻点焓值之比，(due/dx)s为驻点的速度梯度。

2.3.2 沿流线的热流计算方法

本文采用的表面热流计算理论为Zoby[13]发展的基于参考焓理论的层流及湍流计算理论。层流气动热计算公式为：

qwl= 0.22(Reθe)-1(ρ*/ρe)(μ*/μe)·

其中，qwl为所求流线上任一点的热流，ρ*、μ*为参考密度及粘度，ρe、μe为边界层边缘的密度及粘度，Haw为绝热壁面焓，Hw为壁面焓，Reθe为根据边界层外缘参数计算得到的层流动量厚度雷诺数，其中动量厚度根据下式确定：

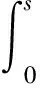
(4)

其中，ue为所求流线上任一点对应的边界层边缘的速度，V∞为自由来流速度，r为尺度因子(拉梅系数)，s为沿流线的积分长度。

湍流气动热的计算公式为

qw t=c1(Reθe)-m(ρ*/ρe)(μ*/μe)m·

其中，湍流动量厚度雷诺数的湍流厚度根据下式得到：

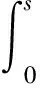
(6)

其中参数m及c1、c2、c3、c4的定义参见文献[13]。

对于尺度因子的求解,假设边界层内的流动方向与物面绕流方向一致，且物面上垂直于流线的流动速度相对于流线方向的速度可以略去，将三维边界层方程简化为轴对称的边界层方程，方程中流线长度作为子午线的长度，垂直于流线的尺度因子即为式中的r，具体求解参见文献[13]。

3 数值计算方法

3.1计算理论

不计质量力情况下，三维直角坐标系中非定常可压缩N-S方程的守恒形式可以写为下列向量式：

其中，U为守恒变量矢量，F、G、H为对流项，Fv、Gv、Hv为粘性项，各项定义具体参见文献[14]。

本文CFD计算格式采用Roe的FDS格式，因其具有较高的粘性分辨率，且收敛性较好。物理流动模型分别为无湍流模型的薄层假设与B-L湍流模型。时间离散采用LU-SGS方法。

3.2计算网格及边界条件

采用的计算网格为多块结构网格，如图4所示，并保证第一层网格的壁面网格雷诺数小于10。网格数量约为350万。

采用的边界条件包括：远场采用外插边界条件；物面采用无滑移的等温壁面条件(Tw=300K,与试验条件一致)；对称面采用镜面反射边界条件。

4 结果分析

利用建立的数值及工程方法计算了空天飞行器在Ma=8.0、10.2，迎角为0°条件下的热流分布，并与试验数据对比。具体计算条件如表1所示。

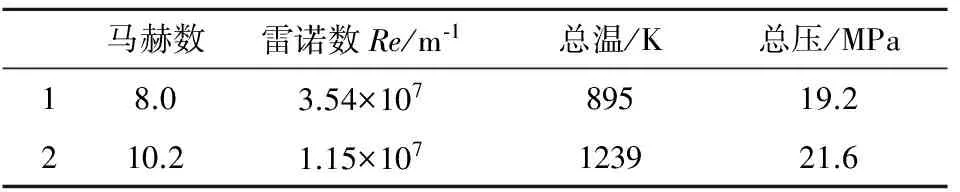
表1 计算条件Table 1 Computational conditions

热流采用无量纲值，参考热流采用书中给定的热流试验值：Ma=8.0时，qref=476.30kW/m2；Ma=10.2时，qref=585.50kW/m2。Ma=8.0计算得到的纵向对称面上、下表面的热流如图5及图6所示。

图5为通过工程方法、数值方法得到的机身纵向对称面下表面热流分布与试验数据的对比(图中laminar-，表示层流气动热的工程计算；turbulent-，表示湍流气动热的工程计算；NS-laminar，表示层流模型数值计算；NS-bl，表示bl湍流模型数值计算)。迎角0°时，下表面是背风面，采用工程方法及数值方法，都可以揭示热流的变化趋势，在两种方法中采用湍流模型的计算结果明显高于无湍流模型的结果。 因为实验数据是在层流状态下的气动热，层流的计算结果与实验数据比较吻合，且数值计算的结果比工程方法更接近于实验值。图6为纵向对称面上表面热流分布，数值与工程方法及实验数据在后半段吻合较好，前半段差别较大。层流的数值计算结果明显优于工程方法，且数值方法与实验数据吻合较好。Ma=10.2得到的纵向对称面热流分布如图7所示。

工程方法或数值方法都可以揭示热流的变化趋势，数值方法中采用层流气动热的计算方法与风洞试验试验数据吻合的较好。工程方法与数值方法及实验数据存在少许差异。图7为纵向对称面上表面热流分布的对比，数值方法及工程方法与实验数据吻合较好，在拐角处差异较大。Ma=8.0得到的机翼II-II截面的热流如图8所示。

通过两种方法得到的计算曲线规律一致，且基本重合，但在机翼前缘附近数值计算的结果高于工程计算得到数值，在存在试验数据的一段内与试验数据吻合较好。表2为通过数值方法与工程方法得到的驻点热流值与试验值的比较，两种方法得到的驻点热流与试验值之间的误差均小于5%。

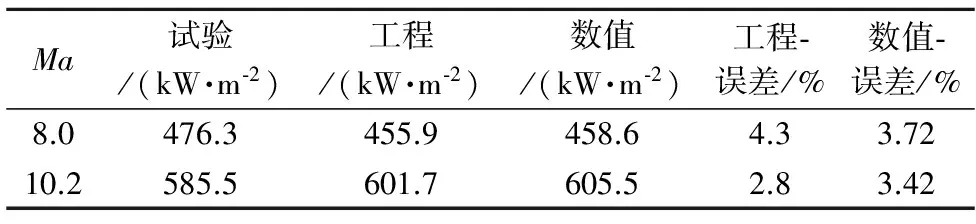
表2 驻点热流对比Table 2 Aerodynamic heating comparisons for stagnation point

5 结 论

针对空天飞行器基本形，建立了高超声速气动热的数值方法及基于表面流线的气动热快速工程方法，表面流线通过基于直角网格的无粘Euler方程得到，得到的结论为：

建立的数值方法及快速工程方法都较好的反映了空天飞行器在高超声速时的气动热分布规律。通过与试验数据的对比，两种方法在层流状态下计算得到的机身与机翼的热流分布与试验数据吻合较好；通过数值计算及工程计算得到的驻点热流与试验值的误差在5%以内。

本文建立的基于表面流线的气动热工程方法计算速度快，计算结果较好，虽然与数值计算方法及实验数据相比，在个别点存在较大的差异，在下一步工作中力求对其进行较为系统的验证，使其成为气动热快速计算的工具。

[1]范绪箕. 气动热与热防护系统[M]. 科学出版社. 2004.

[2]Liu Xin, Deng Xiaogang. Application of high-order accurate algorithm to hypersonic viscous flows for calculating heat transfer distributions[R]. AIAA-2007-691, 2007.

[3]Klopfer G H, Yee H C. Viscous hypersonic shock-on-shock interaction on blunt cowl lips[R]. AIAA-88-0233, 1988.

[4]周伟江, 姜贵庆. 迎风TVD 格式在粘流计算中的应用研究与改进[J]. 计算物理, 1999, 16(4): 401-408.

[5]潘沙, 冯定华, 丁国昊, 等. 气动热数值模拟中的网格相关性及收敛[J]. 航空学报, 2010, 31(3): 493-499

[6]Cohen C B, Reshotko E. Similar solution for the compressible laminar boundary layer with heat transfer and pressure gradient[R]. NACA Report 1293, 1956.

[7]DeJarnette F R, Jones M H. Calculation of inviscid surface streamlines and heat transfer on shuttle type configurations. Part 1 Description of basic method[R]. NASA CR-111921, 1971.

[8]Dejarnette F R, Hamilton H H, Weilmuenster K J. New method for computing convective heating in stagnation region of hypersonic vehicles[R]. AIAA-2008-1261, 2008.

[9]贺国宏, 高晓斌, 庞勇. 高超声速再入体表面热流数值模拟研究[J]. 空气动力学学报, 2001, 19(2): 177-185.

[10]李素循. 典型外形高超声速流动特性[M]. 北京: 国防工业出版社, 2007.

[11]Fay J A, Riddell F R. Theory of stagnation point heat transfer in dissociated air[J]. Journal of the Aeronautical Science, 1958, 25(2): 112-120.

[12]Kemp N H, Rose R H, Detra R W. Laminar heat transfer around blunt bodies in dissociated air[J]. Journal of the Aerospace science, 1959, 26(7): 68-75.

[13]Zoby E V, Moss J N, Sutton K. Approximate convective heating equations for hypersonic flows[J]. Journal of Spacecraft and Rockets, 1981, 18(1): 64-70.

[14]傅德薰, 马延文, 等. 计算流体力学[M]. 北京: 高等教育出版社, 2002.

Computationalmethodonhypersonicaerodynamicheatingforaerospacevehicle

WANG Peng*, FANG Shuai, JIN Xin, ZHANG Weimin

(ChinaAcademyofAerospaceAerodynamics,Beijing100074,China)

Hypersonic aerodynamic heating characteristics for an aerospace vehicle atMa=8.0 andMa=10.2 was calculated by computational fluid dynamics (CFD) method and engineering rapid computational method based on in-viscid surface streamlines. The Roe flux difference scheme(FDS) was employed in the CFD method. For the engineering rapid computational method, the in-viscid surface streamlines were determined by the Euler equations on the Cartesian grid, and the surface heating distribution can be computed by the integration along the in-viscid surface streamlines according to the Eckert reference enthalpy theory. Both laminar and turbulent flows were simulated in the present study. Comparisons were carried out between the engineering rapid computational results, the CFD results, and the experimental results. The results show that the heating distribution can be well predicated for the airframe and the wing of the aerospace vehicle by the CFD method and the rapid engineering method developed in this paper. The error of the aerodynamic heating distribution at the stagnation point is less than 5%.

surface streamline; aerodynamic heating; aerospace vehicle; numerical simulation; engineering method

V211.3

A

10.7638/kqdlxxb-2015.0067

0258-1825(2017)05-0640-05

2015-05-24;

2015-11-26

国家自然科学基金(61273153)

王鹏*(1984-)，男，山东潍坊人，工学硕士，工程师，研究方向：高超声速气动力/热的数值计算和工程估算及嵌入式大气数据传感系统的研究. E-mail：pengwang0413@163.com

王鹏, 房帅, 金鑫, 等. 空天飞行器高超声速气动热特性计算方法[J]. 空气动力学学报, 2017, 35(5): 640-644.

10.7638/kqdlxxb-2015.0067 WANG P, FANG S, JIN X, et al. Computational method on hypersonic aerodynamic heating for aerospace vehicle[J]. Acta Aerodynamica Sinica, 2017, 35(5): 640-644.