改进动态面控制方法及其在过失速机动中的应用

章 胜, 汪 清, 何开锋, 邵元培

(中国空气动力研究与发展中心 计算空气动力学研究所, 四川 绵阳 621000)

改进动态面控制方法及其在过失速机动中的应用

章 胜*, 汪 清, 何开锋, 邵元培

(中国空气动力研究与发展中心 计算空气动力学研究所, 四川 绵阳 621000)

为提高模型飞行试验中飞机过失速机动控制品质，发展了一种考虑非定常气动力效应与舵回路作动器模型的改进动态面飞行控制律。针对一般仿射模型情形的控制律设计了流程：首先针对子系统推导动态面控制律，然后综合全系统并考虑控制约束导出滑模控制律，在一定的假设条件下，证明了闭环控制系统为输入-状态稳定。在应用提出的控制方法进行过失速机动控制律设计中，为准确预测飞机非定常气动力效应，利用过载测量量反解飞机气动力、采用微分方程模型计算飞机非定常力矩。由于综合了作动器动力学模型，控制律的控制效果受作动器带宽影响较小，可以有效消除由作动器动态响应引起的控制效果变差问题，同时控制律中对非定常气动力效应的有效预测也有利于过失速机动品质的改善。

模型飞行试验；过失速机动；非定常气动力；动态面控制；滑模控制

0 引 言

模型飞行试验可以作为验证飞行器性能与技术的一种有效手段[1]。飞机大迎角过失速机动存在气动特性明显非线性、惯性耦合等强非线性因素，传统的基于线性化小扰动理论设计的线性控制律已不再满足要求，需要发展非线性控制律[2]。

非线性动态逆控制律是一种广为研究的方法。研究表明过失速机动中动态逆控制律比线性控制律具有更好的性能[3]。动态逆方法采用时标分离原理将系统分成快、慢回路，快回路增益足够大才能在理论上保证系统的稳定性[4]，但其受制于舵回路的性能，并不能任意取大。基于Lyapunov方法的反步控制律是得到广泛研究的另一种非线性控制律，其对时标分离尺度没有要求[5]，但需要对中间虚拟控制信号进行求导，对于飞行控制律设计问题这是极为复杂繁琐的。对此，学者们进一步发展了动态面飞行控制律，通过引入一阶滤波器近似得到虚拟控制信号的导数[6-7]。

控制律设计中需要用到飞机的气动力模型。过失速机动中飞机迎角会超过失速迎角，此时的空气绕流流场十分复杂，气动力具有明显非定常特征，由静态试验数据、动导数等数据构成的常规气动力模型不能很好地满足过失速机动控制的需要。控制律设计中考虑非定常效应有利于减少气动模型的误差，改善控制效果[8]。另一方面，飞机舵回路作动器动态响应引起的控制滞后可能对控制效果产生不利影响，作动器偏转速率饱和甚至可能诱发飞机振荡[9]，因此作动器响应能力是控制律设计中需要考虑的重要问题。Bates等[10]、Choi等[11]设计控制律时考虑了作动器的动力学响应。Hess等[12]采用速率限制器技术有效消除了舵偏速率约束引起的控制时延，该方法实质是将舵偏速率作为控制量。

本文发展了一种改进的动态面飞行控制律，通过有效预测非定常气动力、考虑作动器动力学模型并采用舵偏速率作为实质控制量，改善了飞机过失速机动品质。

1 数学模型

首先定义主要的飞机相关坐标系。飞机机体系b与飞机固连，原点ob位于飞机质心，obxb轴在飞机对称面内并指向机头，obyb轴垂直于飞机对称平面指向机身右方，obzb轴在飞机对称面内指向机身下方。航迹坐标系h与飞机固连，原点oh位于飞机质心，ohxh轴与飞机速度矢量重合，ohzh轴位于包含飞机速度矢量的铅垂面内，指向下方，ohyh轴通过右手定则确定。地面系g固定于地面，原点og位于地面某点，ogxg轴在水平面内指向某一方向，ogzg轴垂直于水平面并指向地心，ogyg轴通过右手定则确定。

描述飞机迎角α、侧滑角β与绕速度矢滚转角μ的微分方程为[13]:

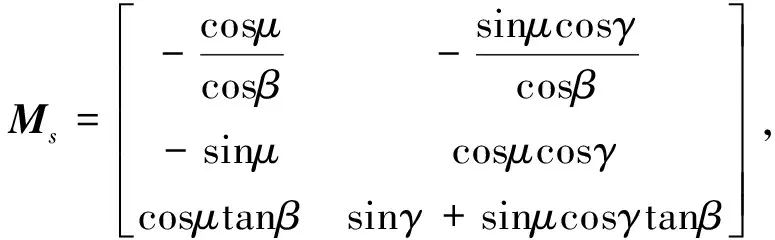
γ为航迹倾角，χ为航迹方位角，它们的微分方程为:

Tx(sinμcosαsinβ+cosμsinα)-

Tx(sinμsinα-cosμcosαsinβ)+

其中，V为飞机速度幅值，D、L与Y分别为飞机受到的升力、阻力与侧向力，Tx、Ty与Tz分别为发动机推力在飞机体系x、y与z坐标方向的分量。

飞机角速度微分方程为：

其中，I为飞机惯量张量，la、ma与na分别为飞机受到的滚转、俯仰与偏航力矩，lt、mt与nt分别为飞机受到的滚转、俯仰与偏航推力矩。式(4)中力矩项可进一步改写为：

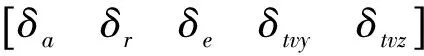
Gf=

其中，Q为动压，S为飞机参考面积，b、c分别为飞机横向参考长度和纵向参考长度，Cl δa等代表相应的操纵导数，如Cl δa表示副翼在滚转方向的操纵导数，(mt)δtvz代表俯仰推力矩对δtvz的偏导数，其它操纵导数意义类推。

飞机姿态控制伺服机构包括气动舵面与推力矢量，它们的作动器模型可以采用一阶惯性环节表示为[14]：

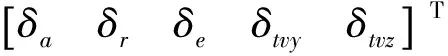
2 过失速机动控制律设计

2.1控制律设计方法

考虑作动器动力学模型后被控对象为3阶系统，文章首先针对考虑控制约束的一般3阶级联仿射系统给出控制律设计流程。考虑如下系统：

其中，x1∈Rn1、x2∈Rn2、x3∈Rn3为状态变量，u∈Rm为控制输入，其受到约束|ui|≤uimax(i=1,2,…,m)，变量维数满足m≥n3≥n2≥n1，f1、f2与f3为相应维度的矢量函数，g1、g2与g3为相应维度的矩阵函数，满足rank(g1)=n1、rank(g2)=n2、rank(g3)=n3，d1、d2与d3为相应维度的不确定项。

不妨设原点为平衡点，本文提出的控制律设计步骤可分为两步：

1) 针对x1、x2系统，将x3视为控制(为与状态区别，用x3d指代)，设计反步控制律[15]:

其中，x2d为中间虚拟控制，其为:

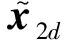
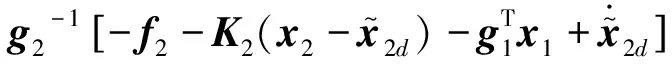
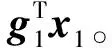
2) 进一步考虑x3状态，基于式(12)定义滑模变量s为:

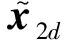
(13)

则通过使滑模变量幅值平方‖s‖2单调减小、并利用最大控制能力可取控制律u为[16]:

(14)

关于闭环控制系统的稳定性，在下述假设条件下，将建模不确定性作为扰动输入，可以证明系统为输入-状态稳定。

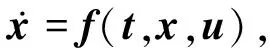
假设1：矢量函数f1、f2、f3，矩阵函数g1、g2、g3均为Lipschitz函数。

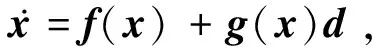
定理1：在假设条件1、2下，存在一定的滤波器时间参数τ，使得采用控制律(14)的闭环控制系统(8)为输入-状态稳定。

证明：因为由Lipschitz函数复合与求和构成的函数也为Lipschitz函数，故存在常数L1与L2，使得：

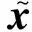
其中，σmin(·)表示矩阵的最小奇异值。构造Lyapunov函数：

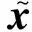
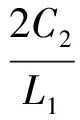
对式(17)求导，有：

利用Young’s不等式，可得：

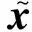
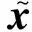
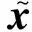
将式(20～24)、(15)代入式(19)并化简，有

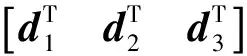
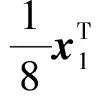
对于q，利用反证法可以证明存在一个常数e>0，使得：

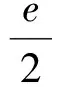
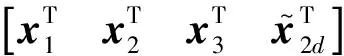
2.2动态面飞行控制律设计

依据2.1节中的控制律设计流程，本文首先针对气流角与角速度回路设计基本动态面飞行控制律。飞机前馈控制指令包括迎角指令αc、侧滑角指令βc与绕速度矢滚转角指令μc，为了提高迎角控制品质，设置迎角指令参考模型[13]：

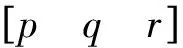
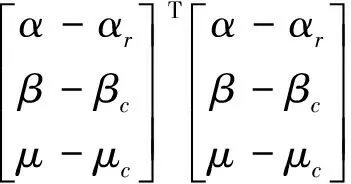
其中，hc为中间虚拟控制，其为：

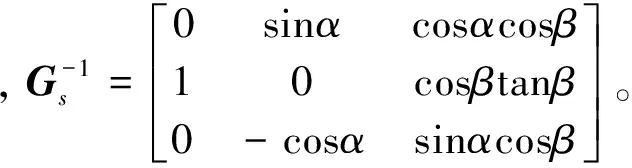
其中，K2为角动量回路增益矩阵。引入一阶滤波器

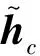
利用式(4)、(5)可以得到舵偏角指令δcmd为：

其中，Gf-1为非方矩阵Gf的广义逆，

2.3改进动态面飞行控制律设计

进一步考虑作动器动力学模型导出滑模控制指令，舵面运动模型为：

其中，va、vr与ve分别为副翼偏转速率、方向舵偏转速率与升降舵偏转速率，vtvy与vtvz分别为偏航推力矢量偏转速率与俯仰推力矢量偏转速率。

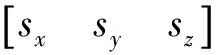
对于俯仰通道相关的升降舵δe与推力矢量δtvz，由于sgn(ab)=sgn(a)·sgn(b)对任意标量a、b成立，同时考虑到符号函数会引起抖振效应，取

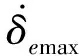
(39)

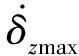
(40)

其中，sgnm()是为削弱滑模控制抖振引入的改进符号函数[16]，其定义为：

其中，ε为边界层厚度。滑模控制中引入边界层会影响s的控制精度，但其仍能保证有界误差，它是滑模控制应用中削弱抖振问题的有效手段。

对于与偏航-滚转通道相关的副翼δa、方向舵δr与推力矢量δtvy，考虑到副翼主要提供滚转力矩，方向舵主要提供偏航力矩，(lt)δtvy一般为0，故取:

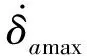
(42)

(43)

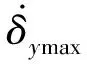
(44)

采用这种控制分配，副翼在偏航通道的干扰项QSbCnδava由偏航推力矢量消除，方向舵在滚转通道的干扰项QSbCl δrvr由副翼消除。

2.4舵偏角指令计算

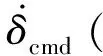
计算舵偏角指令时式(45)中ωδ的数值可能与实际作动器带宽存在误差，这对舵偏指令结果的影响程度是一个需要考虑的问题。分析表明ωδ采用保守取值仅引起控制律中改进符号函数(41)中边界层厚度ε的改变，对控制结果的影响不大，分析如下：

3 非线性、非定常气动力(矩)预测

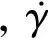
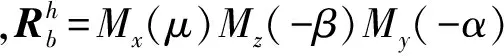
在式(37)中求解滑模变量时需要估计飞机受到的气动力矩，由于过失速机动中气动力非定常效应明显，控制律中内嵌的纵向气动力矩模型除考虑静态与动态气动力矩外，还考虑非定常气动力矩。非定常气动力矩增量Cm,unst采用微分方程模型[18]描述，具体形式为:

其中，k1(α)，e0(α)，e1(α)，f0(α)，f1(α)，g0(α)，g1(α)为与迎角α有关的系数。

4 算例仿真与分析

针对缩比模型飞机进行控制律验证，文章同时还与动态面控制律进行对比，动态面控制律中也采用第3节的方式预测非定常气动力(矩)。仿真计算在Matlab/Simulink平台上进行，其中假设气动模型与推力矢量模型均存在40%的建模误差，同时考虑舵偏位置约束与速率约束。

4.1小迎角跟踪控制

首先针对小迎角控制考察不同作动器带宽参数对控制效果的影响。迎角指令为周期3 s、振幅1°的方波信号，飞机初始迎角为10°，图1给出了飞机迎角对参考迎角的跟踪误差曲线，对于动态面控制律，图中给出了ωδ=20 rad/s、ωδ=40 rad/s与ωδ=+∞(代表理想作动器)三种情形的仿真结果，可以看到随着作动器性能的提高(即带宽的增大)，迎角跟踪误差不断减小；对于本文控制律，由于实质控制量为舵偏速率，ωδ=20 rad/s与ωδ=40 rad/s时的仿真结果重合，最大跟踪误差优于采用理想作动器的动态面控制律约0.01°，虽然数值很小，但也说明本文控制律具有更好的控制效果。

4.2“眼镜蛇”机动

“眼镜蛇”机动是典型的过失速机动，动作简单，便于考验控制律的控制品质。飞机初始迎角为10°，初始侧滑角为0°，机动时长为2.5 s。在0～1 s，αc=70°，1～2.5 s，αc=10°；机动中βc与μc一直为0°，ωδ=40 rad/s，发动机推力为T=200 N。图2给出了迎角仿真曲线，从图中看到采用动态面控制律时，作动器的动态响应过程对仿真结果存在较大影响，而采用本文控制律的迎角仿真结果与采用理想作动器的动态面控制律结果接近，能较好的克服作动器响应滞后对控制效果的影响。

“眼镜蛇”机动主要是纵平面的俯仰运动。图3给出了升降舵与俯仰推力矢量偏转曲线，机动中升降舵与俯仰推力矢量偏转发生了位置饱和与速率饱和；动态面控制律的舵面运动在飞机迎角拉起中比本文控制律结果略有滞后；相较采用理想作动器的动态面控制律，本文控制律满足作动器的性能约束；此外本文控制律的舵面运动曲线总体比较光滑，这说明控制律中采用改进符号函数有效削弱了滑模控制的抖振问题。

考察非定常气动力效应对过失速机动的影响，图4给出了机动过程中的非定常气动力矩示意图，伴随着迎角的改变其大致呈顺时针环形。图5对比了控制器中考虑非定常气动力矩与否的迎角曲线，根据超调量等指标对比，可以看到控制律中考虑非定常气动力效应有利于改善过失速机动品质。

4.3Herbst机动

Herbst机动综合了飞机动态拉起迎角进入过失速状态、大迎角下绕速度矢滚转等基本过失速机动动作，是检验飞机过失速机动能力的标准验证动作。文章进一步针对Herbst机动考察控制律效果，飞机初始迎角为10°，初始侧滑角为5°，机动时长为22 s，机动中βc=0°，αc、μc与发动机推力指令通过跟踪离线优化的轨迹计算[13]，ωδ=40rad/s。图6给出了三维空间中的Herbst机动轨迹，可以看到本文控制律与动态面控制律均较好地实现了180°快速转弯机动。

图7给出了Herbst机动中控制律对迎角与侧滑角的控制误差，两种控制律在迎角深失速区域由于飞机绕速度矢量滚转都出现了一定的误差，不过相较于动态面控制律，本文控制律的误差更小。

图8与图9分别给出了Herbst机动中的气动舵面与推力矢量偏转曲线，可以看到两种控制律的舵面运动总体类似，机动中气动舵面与推力矢量的运动曲线没有明显的抖振现象。

同样考察Herbst机动中非定常气动力效应的影响，图10对比了控制律中考虑非定常气动力矩与否的迎角控制曲线，结果再次表明考虑非定常气动力效应总体上能达到更高的机动控制精度。

5 结 论

本文发展了一种考虑非定常气动力效应与舵回路作动器模型的改进动态面飞行控制律，考察了飞机小迎角控制、“眼镜蛇”机动与Herbst机动，主要结论为：

1) 控制律中对非定常气动力效应的有效预测有利于改善过失速机动品质。

2) 由于综合了作动器动力学模型，控制律对作动器带宽变化不敏感，可以有效消除作动器动态响应引起控制效果变差的问题。

[1]He K F, Liu G, Zhang L H, et al. Research progress on model flight test of powered aircraft with autonomous control system[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 1-7. (in Chinese)

何开锋, 刘刚, 张利辉, 等. 航空器带动力自主控制模型飞行试验技术研究进展[J]. 实验流体力学, 2016, 30(2): 1-7.

[2]Shi Z K. Challenge of control theory in the presence of high performance aircraft development[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2717-2734. (in Chinese)

史忠科. 高性能飞机发展对控制理论的挑战[J]. 航空学报, 2015, 36(8): 2717-2734.

[3]Snell S A, Enns D F, Garrard W L. Nonlinear inversion flight control for a supermaneuverable aircraft[J]. Journal of Guidance, Control, and Dynamics, 1992, 15(4): 976-984.

[4]Schumacher C, Khargonekar P P. Stability analysis of a missile control system with a dynamic inversion controller[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(3): 508-515.

[5]Knoos J, Robinsony J W C, Berefeltz F. Nonlinear dynamic inversion and block backstepping: a comparison[C]//AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2012: 1-20.

[6]Swaroop D, Gerdes J C, Yip P P, et al. Dynamic surface control of nonlinear systems[J]. IEEE Transaction on Automatic Control, 1997, 45(10): 1893-1899.

[7]Liu S G, Sun X X, Dong W H. Design of post-stall maneuvering flight control law based on dynamic surface control[J]. Systems Engineering and Electronics, 2010, 32(10): 2210-2213. (in Chinese)

刘树光, 孙秀霞, 董文瀚. 动态面过失速机动飞行控制律的设计[J]. 系统工程与电子技术, 2010, 32(10): 2210-2213.

[8]Shi Z W, Ying J H, Ming X. The effects of unsteady free stream on the post stall maneuvering aircraft[J]. Acta Aerodynamica Sinica, 2008, 26(4): 486-491.

史志伟, 尹江辉, 明晓. 非定常自由来流对飞机过失速机动特性的影响研究[J]. 空气动力学学报, 2008, 26(4): 486-491.

[9]Li J P, Yang Z X, Luo X. Method to prevent pilot induced oscillations due to actuator rate limiting[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(3): 263-265. (in Chinese)

李建平, 杨朝旭, 罗欣. 作动器速率饱和时的PIO抑制方法[J]. 航空学报, 2003, 24(3): 263-265.

[10]Bates D, Hagström M. Nonlinear analysis and synthesis techniques for aircraft control[M]. Berlin: Springer, 2007: 231-257.

[11]Choi B, Kim H J, Kim Y. Robust control allocation with adaptivebackstepping flight control[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 228(7): 1033-1046.

[12]Hess R A, Snell S A. Flightcontrol system design with rate saturating actuators[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 90-96.

[13]Hu M Q. Research on nonlinear flight control law design of aircraft with vectoring thrust[D]. Xi’an: NorthwesternPolytechnical University, 2002. (in Chinese)

胡孟权. 推力矢量飞机非线性飞行控制律设计研究[D]. 西安: 西北工业大学, 2002.

[14]Chen Y L. Nonlinear dynamic characteristics analysis and control of aircraft at high-angle-of-attack[D]. Nanjin: Nanjing University of Aeronautics and Astronautics, 2007. (in Chinese)

陈永亮. 飞机大迎角非线性动力学特性分析与控制[D]. 南京: 南京航空航天大学, 2007.

[15]Khalil H K. Nonlinear systems[M]. Prentice Hall, Upper Saddle River, New Jersey, 2002: 551-625.

[16]Gao W B. Theory and design method of variable structure control[M]. Beijin: Science Press, 1996: 150-152. (in Chinese)

高为炳. 变结构控制的理论与设计方法[M]. 北京: 科学出版社, 1996: 150-152.

[17]Sontag E D, Wang Y. On characterizations of input-to-state stability property[J]. Systems & Control Letters, 1995, 24(5): 351-359.

[18]Wang Q, Qian W Q, Ding D. A review of unsteady aerodynamic modeling of aircrafts at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2331-2347. (in Chinese)

汪清, 钱炜祺, 丁娣. 飞机大迎角非定常气动力建模研究进展[J]. 航空学报, 2016, 37(8): 2331-2347.

Animproveddynamicsurfacecontrollawanditsapplicationinpost-stallmaneuvers

ZHANG Sheng*, WANG Qing, HE Kaifeng, SHAO Yuanpei

(ComputationalAerodynamicsInstituteofChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China)

To enhance the flying quality of aircraft post-stall maneuver in a model flight test, an improved dynamic surface flight control law was proposed in consideration of the unsteady aerodynamics effect and the actuator model. The controller designing procedure was established for general affine models. In the procedure, the dynamic surface controller for the sub-system was first developed. Then the slide mode control technique was employed to synthesize the whole system with the control limitation. The closed system was proved to be input-to-state stable under certain conditions. To accurately predict the unsteady aerodynamics in the post-stall maneuver controller designing, the overload measurement was used to solve the aircraft aerodynamic force, and the differential equation model was developed to compute the unsteady aerodynamic moment. The control effect of the proposed controller is nearly independent of the actuator bandwidth due to the inclusion of actuator model, and the lag effect from the dynamic response of the actuator is effectively attenuated. The valid prediction of the unsteady aerodynamics is also helpful to improve the quality of the post-stall maneuver.

model flight test; post-stall maneuver; unsteady aerodynamics; dynamic surface control; sliding mode control

V249

A

10.7638/kqdlxxb-2017.0092

0258-1825(2017)05-0718-09

2017-05-23;

2017-09-20

章胜*(1986-)，男，四川人，博士，助理研究员，研究方向：飞行器控制与轨迹优化. E-mail: zszhangshengzs@hotmail.com

章胜, 汪清, 何开锋, 等. 改进动态面控制方法及其在过失速机动中的应用[J]. 空气动力学学报, 2017, 35(5): 718-726.

10.7638/kqdlxxb-2017.0092 ZHANG S, WANG Q, HE K F, et al. An improved dynamic surface control law and its application in post-stall maneuvers[J]. Acta Aerodynamica Sinica, 2017, 35(5): 718-726.