远洋干线班轮航速与航线配船优化模型与算法
2017-10-30邢玉伟杨华龙
邢玉伟, 杨华龙, 张 燕
(大连海事大学 交通运输管理学院,辽宁 大连 116026)
远洋干线班轮航速与航线配船优化模型与算法
邢玉伟, 杨华龙, 张 燕
(大连海事大学 交通运输管理学院,辽宁 大连 116026)
针对燃油价格剧烈波动条件下的远洋干线集装箱班轮航速和航线配船优化问题,通过分析远洋干线各航段货运量与港口对需求量、班轮航速与航线配船数量及燃油消耗量之间的关系,构建班轮航速与航线配船优化非线性规划模型,并设计逐步逼近求解算法,通过实例分析验证模型和算法的有效性及适用性。结果表明:基于航速优化策略,通过在不同航线上合理地配置船舶类型和数量,可明显降低班轮运输成本;依据燃油价格变化,适时采取“加船减速”或“减船加速”策略,可有效提高船公司的经济效益。
水路运输;班轮航速;航线配船;非线性规划;逐步逼近算法
在集装箱班轮运输中,燃油成本在班轮运营总成本中占有很大的比重[1],且班轮燃油消耗与航速的三次方成正比[2]。因此,在燃油价格剧烈波动的条件下,调整班轮航速和优化航线配船已成为船公司经营的重大决策。
PERAKIS等[3]和JARAMILLO等[4]提出航线配船问题,并针对该问题建立整数线性规划模型;杨秋平等[5]在此基础上将船队短期调配使用和长期发展规划结合起来进行航线配船与船队规划;MENG等[6]考虑需求因素,假定航线货运需求服从正态分布,建立包含机会约束的短期航线配船整数线性规划模型;NG[7]则进一步放宽对航线货运需求概率分布的限制,探讨需求均值和方差已知情况下的航线配船优化模型。上述研究从不同的角度构建航线配船线性规划模型,并设计相应的求解算法,虽然具有一定的合理性,但都将航速设为定值;同时,班轮往返航次时间和航次成本也被当作常数。这显然与近期船公司在燃油价格波动下采取航速调整策略的现实情况不相符。
航速变化对船队规划决策有很大的影响,航速与航次往返时间、航线配船数量及航次成本都有一定的关系[8],已有学者将班轮航速作为决策变量引入到航线配船问题的研究中。RONEN[9]结合班轮运输实际建立航速优化模型,并设计简单的逼近算法进行求解(该研究仅考虑单一航线、单一船型的情形,尚未对船公司多航线、多船型下的船队航线配船问题展开研究)。WANG等[10]在班轮运输网络中对航速进行优化,将船舶数量作为决策变量建立混合整数非线性规划模型(该研究假定各航线上所配船舶的类型既定,没有考虑航运市场需求及燃油价格波动因素对航线适配船型的影响,难以保证航线配置船型合理)。杨忠振等[11]针对不同市场环境,构建假定船队规模不变情况下的航线配船与航速优化模型(由于航运市场环境瞬息万变,班轮船队规模调整也时有发生,因此该研究模型的适用性不强)。此外,已有研究大多假定航线货运量已知或将港口对需求量进行简单加总作为航线货运量,没有专门依据洲际间集装箱班轮运输的特点对远洋干线各航段货运量与港口对需求量间的关系进行分析,使得航线配置船舶的运力资源与运量要求的符合度不够精细。
综上,在已有研究的基础上,结合集装箱班轮航运的实际,在船舶数量可变的情况下,基于航速调整策略,通过分析远洋干线各航段货运量与港口对需求量间的关系、航速与往返时间及配船数的关系、航速与船舶燃油消耗的关系等,构建多航线、多船型条件下的以船队每周总成本最小化为目标的航线配船与航速优化模型,并设计相应的算法求解,为船公司班轮航线配船与航速优化决策提供参考。
1 问题描述及假设
远洋干线班轮航线通常是一个循环的洲际闭环航线,航线配船与航速优化决策就是在技术可行的基础上考虑到燃油价格等因素,设计出各条航线最优的班轮航速和航线配置方案,使船公司班轮运营成本最低,以获得最佳的经济效益。
问题的基本假设为:
1) 船公司在某洲际海域内经营多条远洋干线,各条远洋干线上挂靠的港口的顺序已知,洲际两端之间港口的集装箱需求量已预测或确定。
2) 各航线上的发船频率均为每周1班,班轮1个往返航次应为周的整数倍。
3) 班轮公司既定类型的船舶都需投入运营,同一航线只能配置同种类型的船舶。[9]
4) 班轮航速是均匀的,不同航段上的燃油消耗与航行速度的函数存在差异[12],这里假定同种船型的船舶在各航段上的燃油消耗函数是一致的。
2 模型与算法
2.1参数及变量

定义参数及变量之后,对变量之间的关系进行分析。
2.1.1航段货运量与港口对间集装箱需求量的关系
根据问题描述,在航线r上,若班轮在所有港口均只挂靠1次,则其中一种航线结构可由图1表示。
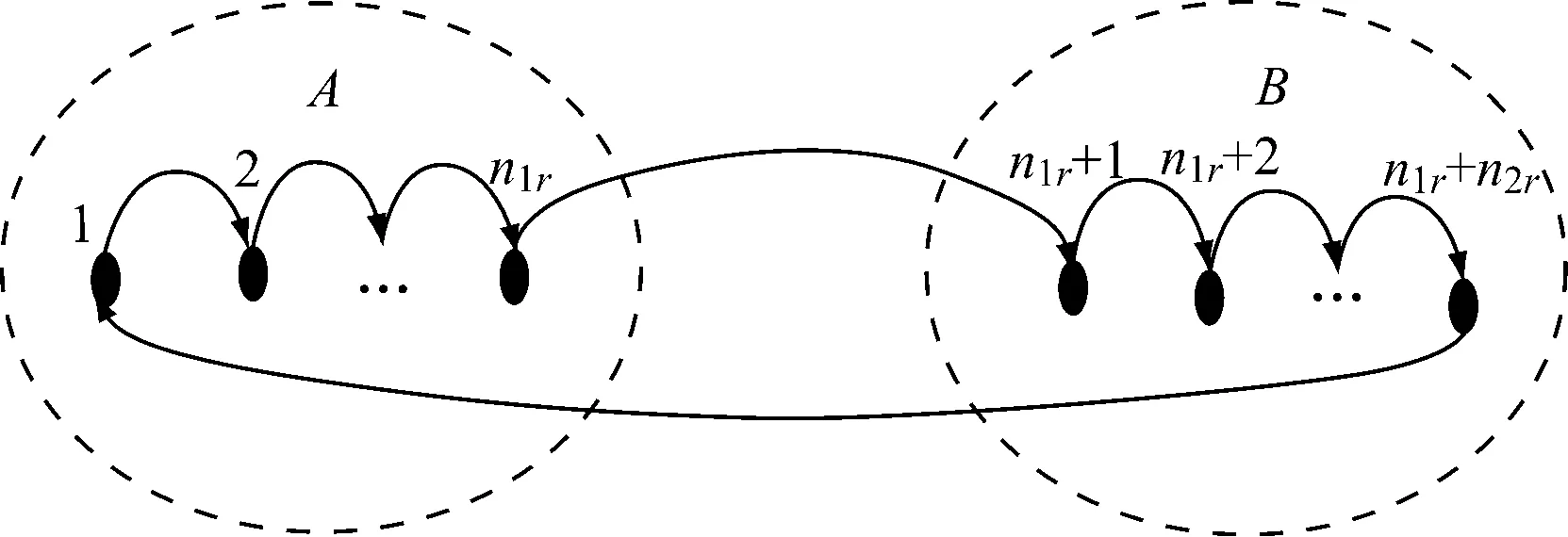
图1 一种航线结构
图1中,虚线圆圈内的港口在洲际航线的一端,这些港口之间没有货物流动,在航线r上,假设A端有n1r个港口,B端有n2r个港口,则航线共有n1r+n2r个航段,于是在航线r的各个航段上航段货运量与港口对间集装箱需求量的关系可表示为
(1)
在航线r上,若班轮在某枢纽港挂靠2次,在其余港口均挂靠1次,则另一种航线结构可由图2表示。

图2 另一种航线结构
图2中,虚线圆圈内的港口在洲际航线的一端,这些港口之间没有货物流动,在航线r上,假设A端有n1r个港口,B端有n2r个港口,且第n1r个港口被挂靠2次,第1次挂靠港口n1r时只有装货,第2次挂靠港口n1r时只有卸货,则航线共有n1r+n2r+1个航段,于是在航线r上的各个航段内,航段货运量与港口对间集装箱需求量的关系可表示为
(2)
2.1.2航速与往返时间及配船数的关系
船舶在各航线上每航次的往返时间由海上航行时间及在港口的靠港停泊时间组成,即
(3)
远洋干线班轮航线通常都是以周班频率发船的,因此配置到r航线上的v型船的数量可表示为
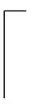
(4)

2.1.3航速与船舶燃油消耗的关系
燃油成本包括副机的柴油成本和主机的重油成本。同种类型船舶的周副机耗油量为定值,主机发动机功率与航速近似成三次方的关系[11],即
PM=0.735 5D2/3s3/C
(5)
式(5)中:PM为发动机的实际功率,kW;D为船舶的排水量,t;C为海军常数。单船主机的日均重油消耗与主机功率成正比[12],即
Ff=24×10-3PMg=17.652×10-3gD2/3s3/C
(6)

(7)
2.1.4船队成本构成
班轮公司的船队成本分为固定成本和变动成本,其中固定成本对航线配船决策没有影响,因此只考虑变动成本,即燃油成本和船舶的营运成本。
燃油成本包括副机的柴油成本和主机的重油成本。[11]若运营时每种类型船舶的周副机油耗为Flv,则每艘v型船的燃油成本可表示为
PlFl,v+7PfFf,v
(8)
船舶的营运成本包括船员工资、日常船舶维修及保养费、管理费用等,航线所配船舶数量不同,其营运成本也必定不同。若每艘v型船的日营运成本表示为Cv,则在r航线上的船舶周总运营成本可表示为

(9)
2.2模型构建
通过以上分析,可建立以下航速与航线配船优化模型。
1) 目标函数为

(10)
2) 约束条件为

∀r∈{1,2,…,R}
(11)
r∈{1,2,…,R}
(12)
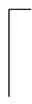
r∈{1,2,…,R}
(13)
Smin,v≤sv≤Smax,v,∀v∈{1,2,…,V},
r∈{1,2,…,R}
(14)
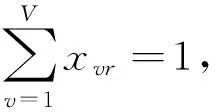
(15)
xvr∈{0,1},∀v∈{1,2,…,V},
r∈{1,2,…,R}
(16)
式(10)为船公司在各航线上的船舶周总运营成本最小化;式(11)为船舶运载能力的约束,即配置在r航线上的船舶运载能力不小于任意航段的货运量;式(12)为航速与船舶完成一个航次的时间关系,每个航次的时间包括船舶在港停泊时间及海上航行时间;式(13)为航线配船数量约束,即所配的船舶数量一定要满足周班的发班频率;式(14)为速度约束,班轮船舶在技术上都有最低航速和最高航速的限制;式(15)为每条航线上只能配置同种类型的船舶;式(16)为是否将v型船配置到r航线上。
2.3算法设计
从目标函数及约束条件中可看出,构建的上述模型属于非线性混合整数规划模型,不仅包含整数型变量和连续型变量(航线配船数为整数型变量,航速为连续型变量),而且式(10)和式(12)、式(13)均是非线性的,同时式(13)存在向上取整的特点。因此,需设计有效的算法加以求解。
考虑到现实中船公司在某特定洲际海运区域内运营的远洋干线班轮航线数量和配置的船型种类等极其有限,且航速可进行离散化处理[10],因此设计一种结合枚举的逐步逼近算法对模型进行求解,具体步骤如下。
1) 按顺序对航线和船型进行编号;用枚举法找出R条航线按编号组成的所有R!=R·(R-1)·…·1个排列;从排列1开始,对每个排列j(j∈R!),按航线编号在排列中的先后顺序逐一对各条航线进行配船,配船时按船型编号的先后顺序进行。
2) 依顺序选定的排列a,将依顺序选定的v型船配置在依顺序选定的r航线上,从最大航速Smax,v开始,即令sv=Smax,v,利用式(13)计算出需在该航线上配备的v型船数量nm,vr,通过式(11)判断在该航线上配置v型船能否满足每周的货运量需求。若不满足,则转入步骤5;若满足,则利用式(8)计算出该航线的总成本cm,r,并记ca*,r=cm,r,sa*,v=sv,na*,vr=nm,vr。
3) 减小该型船航速0.1 kn,即令sv=sv-0.1,利用式(13)计算出在该航线上需配备的该型船数量ne,vr,利用式(9)计算出该航线的总成本ce,r。若ce,r 5) 将船型v+1,…,V重新编号为v,…,V-1,v重新编号为V,转入步骤2)。 3.1方案求解 某船公司经营3条亚欧远洋集装箱班轮航线,每条航线的航距及港口挂靠顺序见表1。 表1 航线的航距以及港口挂靠顺序 各航线上洲际间港口对的集装箱需求量可由货源调查和预测得到,限于篇幅,这里从略。 3条航线各航段的货运需求量统计在表2中。该船公司有3种类型的集装箱班轮,每种船型其最大载箱量、营运成本、燃油消耗常数及最大航速和最小航速等数据见表3。 表2 各航线的航段货运量 TEU 表3 船舶参数 船舶在各个挂靠港口的停泊时间均为2 d,重油价格为350美元/t,柴油的价格为650美元/t。利用上述模型和算法对问题进行求解,若不考虑航段货运量的约束,则得到航线配船情况见表4。 表4 航线配船情况 由表4可知:虽然在排列4所对应的方案下船舶周总运营成本最小,但由表2可知,载箱量为6 500 TEU的第3种船不能满足航线2上最大货运量为7 957 TEU的运输需求,因此该方案不可行。同理,排列3对应的方案也不可行。由此可得到,在余下的可行方案中,排列5对应的方案为最优配船方案,即:在航线1上配置10艘7 000 TEU的船舶,最优航速为18.3 kn;在航线2上配置10艘8 000 TEU的船舶,最优航速为19.5 kn;在航线3上配置12艘6 500 TEU的船舶,最优航速为18.3 kn。此时,船舶周总运营成本比排列1对应的方案节省29 932.2美元,说明航速和航线配船优化效果明显。 从上述算例结果中可看出,构建的航速与航线配船模型可较全面地映射航速与燃油成本、航速与航线配船数之间的关系,反映班轮航速变化对航线配船结果产生的影响。设计的算法可方便快速地对该问题进行求解,能满足船公司航速与航线配船决策的实际需要。 3.2燃油价格的敏感性分析 近年来燃油价格波动剧烈,而燃油价格的变化势必会对航线配船产生一定的影响。在上述航线配船结果的基础上进行敏感性分析,航线1上配置的是第2种类型的船舶,将该航线作为研究对象,分别以算例中柴油价格、重油价格10%的幅度变化,可得该航线该型船舶的燃油成本、船舶周总运营成本及航速的变化结果见图3。 从图3中可看出,整体上来说:当燃油价格提高时,班轮最优航速在一定范围内保持不变,但总趋势是最优航速越来越慢;船舶周总运营成本也会越来越高,燃油成本在最优航速不变的情况下会随着燃油价格的升高而增加,在最优航速减慢的转折点处,会出现燃油价格升高而燃油成本降低的情形。 图3 燃油价格对成本及航速的敏感性分析 图4 燃油价格对成本及船舶数量的敏感性分析 在不同的燃油价格下,航线燃油成本、船舶周总运营成本及航线配船数量的变化结果见图4。 从图4中可看出,整体上来说:当燃油价格提高时,最优配船数量在一定范围内保持不变,但总趋势是越来越多;航线总运营成本也会越来越高,燃油成本在最优航速不变的情况下会随着燃油价格的升高而增加,在最优配船数量增加的转折点处,会出现燃油价格升高而燃油成本降低的情形。 本文针对远洋干线集装箱班轮航速与航线配船优化问题,基于航速调整策略,以船公司班轮运营总成本最小化为目标,构建航速与航线配船优化的非线性规划模型,设计结合枚举的逐步逼近算法对模型进行求解,并选取某船公司3条典型的远洋干线进行实例分析。结果表明:在满足各航线货运需求的情况下,当燃油价格较高时,若减速使船公司燃油成本的节约值大于加船使其班轮固定成本的增加值,则船公司应采取“加船减速”策略;而当燃油价格较低时,若加速使船公司燃油成本的增加值小于减船使其班轮固定成本的节约值,则船公司应采取“减船加速”策略。 航速的变化可能会影响到需求的变化,该研究是在港口对需求量确定的情况下进行的,需求不确定及各航段航速变化情况下的航线配船优化问题是下一步研究的方向。 [1] RONEN D.The Effect of Oil Price on Containership Speed and Fleet Size[J].Journal of the Operational Research Society,2011,62(1):211-216. [3] PERAKIS A N,JARAMILLO D I.Fleet Deployment Optimization for Liner Shipping Part 1.Background,Problem Formulation and Solution Approaches[J].Maritime Policy and Management,1991,24(3):183-192. [4] JARAMILLO D I,PERAKIS A N.Fleet Deployment Optimization for Liner Shipping Part 2.Implementation and Results[J].Maritime Policy and Management,1991,18(4):235-262. [5] 杨秋平,谢新连,苏晨.航线配船与船队规划模型及算法实现[J].中国航海,2009,32(1):91-95. [6] MENG Q,WANG T.A Chance Constrained Programming Model for Short-Term Liner Ship Fleet Planning Problems[J].Maritime Policy and Management,2010,37(4):329-346. [7] NG M W.Container Vessel Fleet Deployment for Liner Shipping with Stochastic Dependencies in Shipping Demand [J].Transportation Research Part B:Methodological,2015,74:79-87. [8] 杨秋平,谢新连,裴光石.考虑船舶航速的船队规划非线性模型[J].华南理工大学学报(自然科学版),2011,39(10):119-126. [9] RONEN D.The Effect of Oil Price on Containership Speed and Fleet Size[J].Journal of the Operational Research Society,2011,62(1):211-216. [10] WANG S,MENG Q.Sailing Speed Optimization for Container Ships in a Liner Shipping Network[J].Transportation Research Part E:Logistics and Transportation Review,2012,48(3):701-714. [11] 杨忠振,郭利泉,董夏丹.不同市场环境下的班轮航线配船与航速优化[J].中国航海,2015,38(4):110-115. [12] 叶德亮,黄有方,胡坚堃.低碳模式下班轮航线配船问题研究[J].华中师范大学学报(自然版),2015,49(2):322-326. OptimizationModelandAlgorithmofContainershipSpeedandFleetPlanningonOceanRouteBasis XINGYuwei,YANGHualong,ZHANGYan (Transportation Management College,Dalian Maritime University,Dalian 116026,China) Taken the sharp fluctuation of bunker fuel price into account,the relationship between container transportation volumes of each leg and OD flow between any two ports is analyzed.The relationships among the containership speed,the number of deployed containerships and fuel consumption are illustrated.A nonlinear programming model is established to optimize the containership speed and fleet planning.To solve the model,a successive approximation algorithm is devised.A case study verifies the effectiveness and applicability of the proposed model and algorithm.Experiment results show that the liner shipping costs can be reduced significantly by the speed optimization strategy,allocating reasonable types and number of containerships in different routes.In view of the changes of fuel price,liner companies should appropriately chose the strategy of "adding ship and slow down its speed" or "reducing ship and accelerate its speed",which will effectively improve their economic benefits. waterway transportation;containership speed;fleet planning;non-linear programming;successive approximation algorithm U692.3 A 2017-01-10 国家自然科学基金(71372088;71202108) 邢玉伟(1990—),女,辽宁朝阳人,博士,主要从事交通运输现代化管理研究。E-mail:xingyuwei1990@163.com 杨华龙(1964—),男,辽宁大连人,博士生导师,博士,研究方向为交通运输规划与管理。E-mail:hlyang@dlmu.edu.cn 1000-4653(2017)02-0119-06

3 算例分析
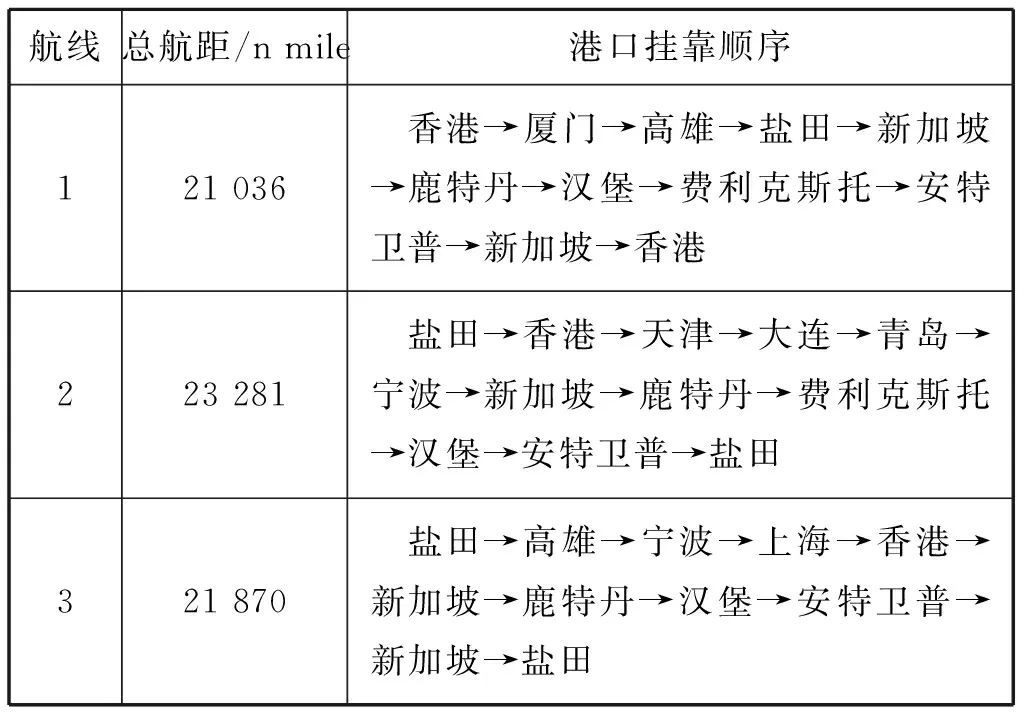


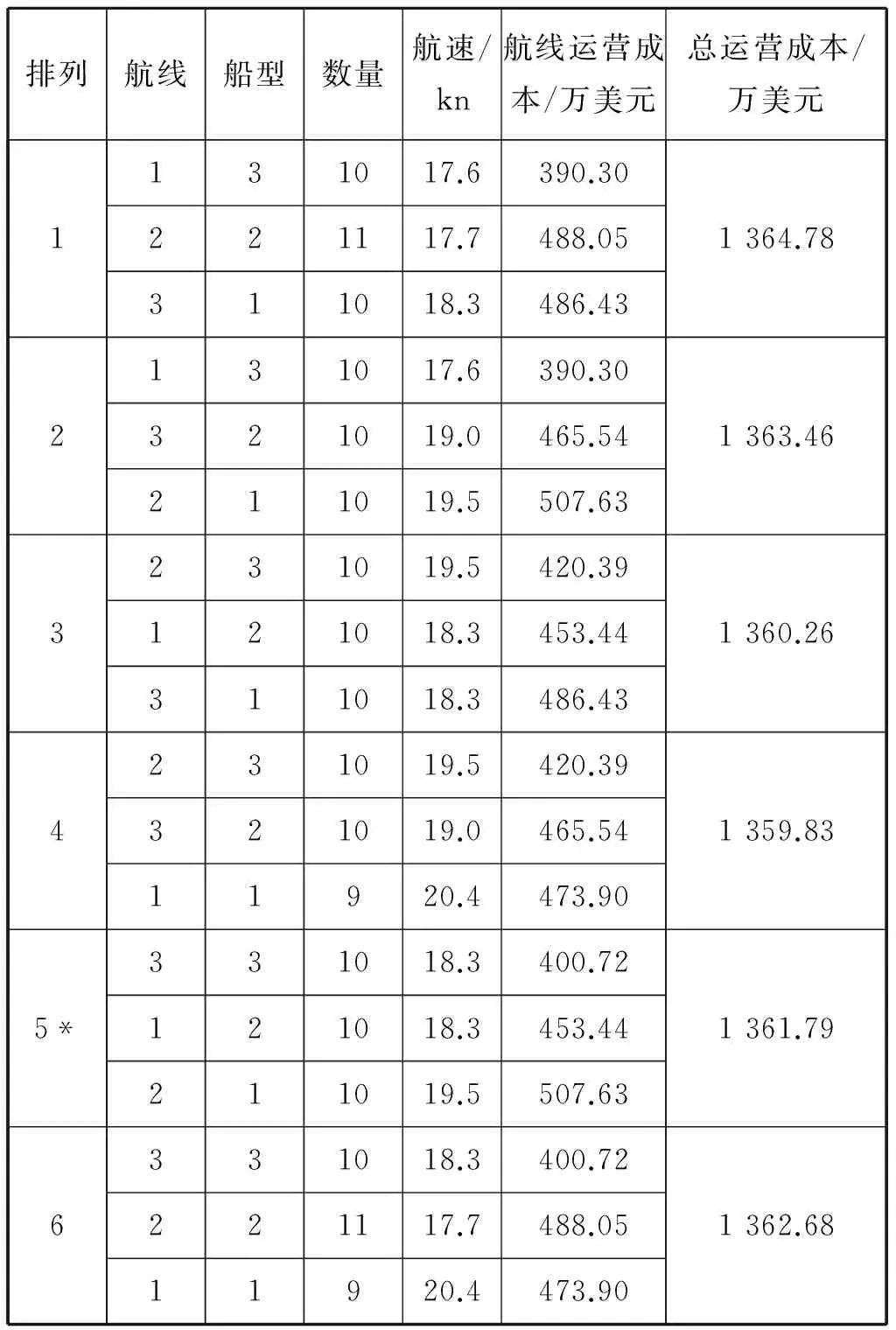


4 结束语
