山区高速公路高填方路堤安全风险评价研究
2017-10-29郭晓魁
郭晓魁
(山西省公路工程质量检测中心,山西 太原 030006)
0 引言
20世纪中后期,我国经济发展进入前所未有的快车道。同时,高速公路的建设也得到了蓬勃发展,全国高速公路总里程也居于世界前列[1]。预计十三五时期,我国西部地区路网覆盖将更加全面、各项基础设施建设将更加完善,运输服务水平将得到显著提升[2]。由于受到地形地貌影响,山区高速建设过程中会有大量的高填方路堤施工,同时由于各方面复杂因素的交叉作用,路堤变形过大和失稳破坏的工程风险问题较多。因此,对于多山地区的此类路堤安全风险评价模型具有相当大的研究价值,并以此来指导山区高速公路等地高填方路堤的实际工程,对路堤的风险防范与管理实现动态化可预测化管理,具有非常重要的理论价值和现实意义。
“风险分析”是在第一次世界大战后,由于战争对于城市的破坏严重,在以德国为代表城市重建工作中应运而生的,1931年美国首次提出“风险管理”理念,风险管理和保险问题便由此被大家所渐渐熟知。在20世纪中叶西方各国对于风险分析研究开展了大量研究,在工程中主要集中在边坡的稳定性评估的风险评价体系,直到2000年,A.Uromeihy and M.R.Mahdavifar[3]通过建立考虑多种影响因素的模糊集理论模型,计算潜在风险指标值。我国从20世纪80年代通过对结构工程和水利水电工程的风险决策,开启了我国的风险分析研究。吴世伟[4]、刘玉恒[5]、汪敏[6]、陈祖煜[7]等人先后对于边坡的稳定风险问题进行了深入研究,并各自提出了相应的评价方法。但通过国内的研究现状可以看出,不同学者的研究角度、研究重点不同,因此,灾害风险分析研究当前还不是很成熟,分析理论还不是很健全。特别是对于高填方路堤方面的的研究还很欠缺,相关理论方面的研究也比较欠缺,实践应用没有完全实现。本文主要介绍以突变理论为基础的风险综合评价模型,分别通过理论推导和在实际工程的应用来说明上述方法的合理性。
1 理论分析
当前对于高填方路堤的失稳风险控制还不是很完善,尤其对于一些不确定性因素引起的风险仍然采用不同施工技术来控制,对于风险分析的理论研究还很匮乏。在实际工程中,路堤失稳风险在施工进行中时有发生,轻则财产损失,重则人员伤亡。然而,高填方路堤的失稳破坏的表现形式大多数为一种非线性动力学的机制。因此,对于此类问题可用突变理论给予分析。突变理论主要运用拓扑学和奇点理论对于不连续现象进行研究。本章利用此理论在非单一目标决策上的优越性这一特征,将其与综合评价相结合,以路堤施工现场检测资料为依托建立了多层次评价体系,对承赤高速公路高填方路堤现场施工过程中的安全进行风险评价,通过分析监测数据的变化,可以分析路堤安全稳定状态及变化趋势。
突变数学由法国科学家雷内·托姆(Rene Thom)于70年代创建,作为一门研究突变的新的数学形式,其建立在微积分、奇点理论、拓扑动力学等数学理论的基础上,对于不连续变化、突变现象等问题进行专门研究[8]。主要方法是以一个系统的势函数为基础,将其边界点进行归类,以便于探索不同类型边界点临近位置的间断性变化特点,因而总结出几个不同形式的初等突变模型。其特点是首先通过多层次矛盾拆分的方法将所分析系统的评价指标进行分解,再通过归一公式对上述分解后的各指标进行整合并将其量化运算,最终得出一个参数,即为总的隶属函数,来对整个系统进行综合评价[9]。该方法的优点是在考虑各因子之间相对重要度时没有采用权重的分配方法,从而使评价分析减少了人为主观性而又不缺乏科学性,因此更符合实际。
雷内·托姆最初归纳了7个突变模型,后来又引申为11个,表1为最初的7个突变模型及势函数。
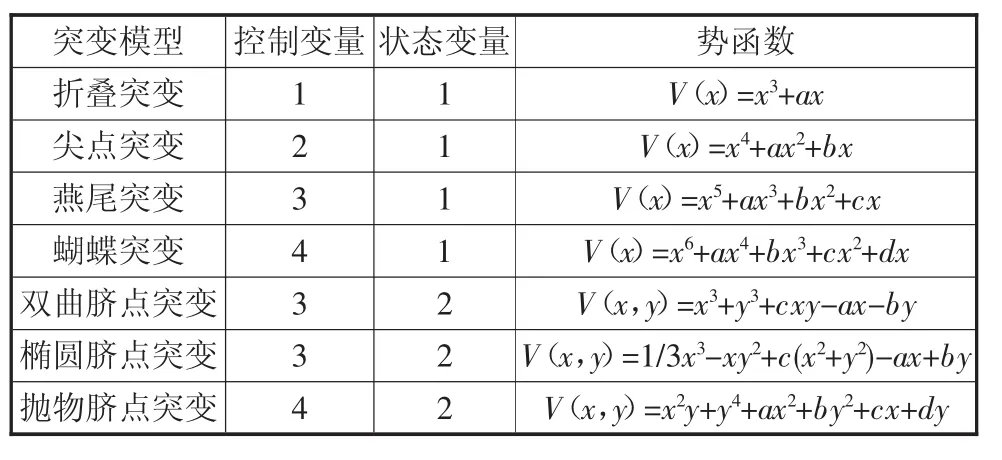
表1 突变模型及其势函数
下面简单介绍突变级数法的实施方案[9]。
1.1 评价体系建立
对评判系统或总指标按照某一原则进行分解,得到由若干个评价因子组成的多层次评价体系,按照重要程度的先后顺序将所包含的评价因子排成树状结构。具体做法是通过逐层分解的方法将评价目标分解到可量化指标即可以停止。这是因为一般上层指标不很明确,较难定量地进行分析,因此需将这些上层指标进行分解得到能够定量分析的具体指标。同时需注意对单个上层因子分解后得到的下层因子的个数不要超过4个,这是因为突变模型中的控制变量最多为4个,这样才能用到匹配的突变模型。
1.2 突变模型
在确定了评价体系结构后,根据每一层评价因子的个数确定与之匹配的突变模型,如表1中所示。通常我们用到的突变系统类型主要为3种。这3种模型的结构示意如图1所示,相对应的模型函数表示为式(1)~式(3)。
尖点突变模型:
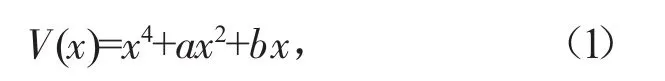
燕尾突变模型:
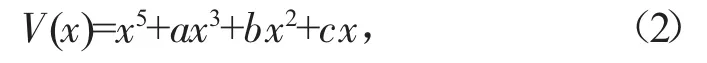
蝴蝶突变模型:
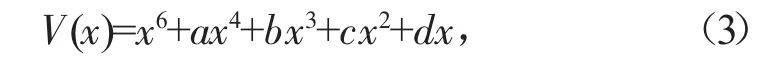
式中:V(x)为某一系统的势函数;x 为状态变量;a、b、c、d为状态变量系数,表示该状态变量的控制变量。有两个相互矛盾的主体存在于模型势函数中,其分别为状态变量和控制变量,并且相互作用影响又存在于各控制变量之间。

图1 3种突变模型示意图
1.3 归一公式确定
对应的归一公式可通过对模型的分歧集方程进行演算求得。V(x)设为系统势函数,由突变理论可得出一平衡曲面可由其全部边界点组成,通过对上述函数求一阶导数后可得到曲面方程,即V′(x)=0;通过求二阶导数即可以等到相应的奇点集合,即V″(x)=0;而后通过联立求解上述两个方程后,即可得出突变系统的分歧点集方程。该方程说明系统的各控制变量在满足上述条件时就会发生突变。最后模型的归一公式经过计算得到式(4)~式(6)。
尖点突变模型归一公式为:
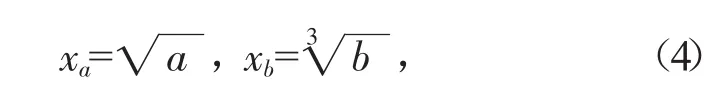
燕尾突变模型归一公式为:
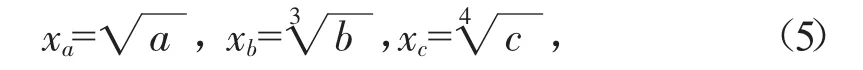
蝴蝶突变模型归一公式为:

式中:xa、xb、xc、xd分别为各式对应于 a、b、c、d时x的值。
1.4 综合评价时对于归一公式的使用条件
根据评价体系中每一层评价因子的个数确定相匹配的初等突变模型,并从最底层的评价因子开始利用归一公式进行评判。在评判中应遵循3种评价原则:互补原则、非互补原则、过阀值后互补原则。
利用归一公式对上层评价因子分解后的各个下层评价因子计算,得到相应的值,并根据因子之间的关系及对上层因子的影响分别采用上述3种原则之一。当某一级下层的各个因子之间无条件相互补充不足,使x值平均值较高,这时即满足了互补原则,突变级数可直接取评价因子归一后的“平均值”;当这些因子不能相互之间补充对方的不足,即符合了非互补原则,因而评价因子归一后按照大中取小的方案获得它的“最小值”,在此条件下对于分歧方程予以满足,最终发生质的改变;各指数及其x值在符合特定的阀值条件时才能相互补充,此时即符合了过阀值后的互补原则。
2 现场监测方案
承赤高速主线是蒙冀界至承德,修成后计划通车里程111.362 km。工程修建通车后,对于完善河北省高速公路网主骨架乃至于全国高速公路网都有非常重要的意义。通过对承赤高速公路现场的多次踏勘,将此次监测的场地选择在承赤高速第七标段和第九标段的高填方路段,其中第七标段路堤平均高度为18.0 m,第九标段的两个路堤分别为12.65 m和14.7 m。根据研究目的,确定本次监测的主要内容有:道路路基基本沉降量的监测、土体承受载荷应力状态的监测、施工土体侧向位移的监测。
根据现场场地的实际情况,为满足高度要求,同时便于观测,将承赤高速第七合同段高填方监测段选定在020涵洞附近区域。分别对于上述的三方面主要检测内容进行检测,对于沉降、侧向位移以及承载力分别设置了3个、2个和12个监测点。其示意图如图2所示。

图2 监测项目设置平面布置示意图
由于施工过程中的监测数据作为其稳定性控制的主要依据,因此采用燕尾突变模型对首层指标进行评价,主控参量为监测数据(B),边坡形态(C),其次,填料性质(D)的影响放在最后,因为该评价体系是以施工期监测数据的变化为主要研究对象,监测数据为主要依据,因此填料的性质变化影响最小。其中侧向变形(B1)、竖向位移(B2)、土压力(B3)等作为下层指标。侧向变形和竖向位移是路堤稳定最直观的因子,路堤边坡的稳定状态与侧向变形的速率息息相关,而路堤整体的稳定性与路堤的沉降(竖向位移)密不可分。土的压力变化也可以反映施工填筑速率的大小及地基土的受力状态。路堤稳定性发现问题时上述3项指标随机会出现异常。对于高填方路堤的边坡稳定是以侧向变形为主,竖向位移次之,土压力是为了了解地基的情况故影响程度最小,这3项因子采用燕尾突变模型。对于高填方路堤的边坡是在设计阶段确定的边坡坡度和路堤高度,且坡度一般按照相关规范选取,因为高度是随填筑过程而增加的,坡度变化较小,因此边坡形态对路堤的安全影响坡高(C1)大于坡角(C2),这两项因子采用尖点突变模型。路堤填土的特性对路堤影响主要是以黏聚力(D1)、内摩擦角(D2)来体现的,通过已有的多数研究显示,黏聚力是影响路堤土稳定性的主要因素,其次为内摩擦角,所以这两项因子运用尖点突变模型。
3 实例计算与分析
限于篇幅原因,本文重点对承赤高速第七合同段的高填方路堤施工期的数据进行计算分析。同时由于检测数据量较大,且为了适应本文的计算方法,选择沉降检测断面2范围的监测项目所获取的监测数据为主要分析对象。因为该路堤断面基本为对称结构,故选择一半的数据作为参考量。本文是以施工期的路堤安全风险评价为研究对象,随着施工的进度进行连续的评价分析,因此需要按照填筑的时间序列进行分析。为满足各监测项目在时间上的一致,选取合适的时间点进行分析。通过分析监测资料,可以分析路堤的变形情况,推断变化趋势及不利的结构面位置,从而反馈到风险评价中[10]。故选取的时间段序列为 Ⅰ :2012-07-19—2012-07-23; Ⅱ :2012-07-23—2012-07-28;Ⅲ:2012-07-28—2012-08-02。
3.1 评价因子初始值选取
3.1.1 测斜管数据分析
为了便于直观地分析测斜管上监测数据的变化,对各测点的水平位移时间变化的分析选取奇数点的监测值,并绘制随时间推移水平位移变化曲线如图3,其中监测日期以横坐标表示。其中测斜管水平位移监测数据变化曲线如图4。

图3 各测点水平位移变化
从图3、图4中不难看出伴随测斜管深度和填筑高度的不断增加,累计水平位移也呈增大趋势,因为测斜管的安置位置是在路堤边坡上,因此可以反映出路堤底部的侧移要大于上部区域。各测点的位移增长率基本为线性增长,在填筑期的位移增长率没有减小的趋势。
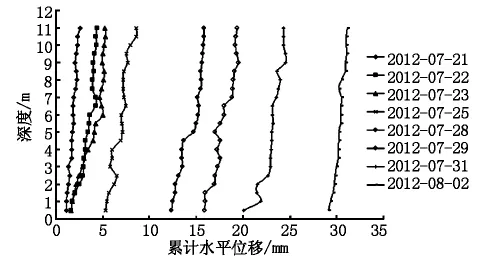
图4 累计水平位移变化
为了便于分析变形速率的变化,将Ⅰ、Ⅱ、Ⅲ时间段的数值变化速率进行了分析,发现变形速率较大的监测点主要集中在路堤底部区域,还有零散地分布于中部的测点。为了方便对比,均取底部2 m区域的最大的3个变形速率的平均值作为评价因子的初始值。因此计算出结构变形速率分别为:Ⅰ期间vⅠ=1.56 mm/d,Ⅱ期间 vⅡ=2.19 mm/d,Ⅲ期间 vⅢ=3.21 mm/d。
3.1.2 沉降管数据分析
根据求得的测点1、测点2、测点3在Ⅰ期间的变形速率分别为 1.99 mm/d、2.65 mm/d、3.35 mm/d;Ⅱ期间的变形速率为 1.15 mm/d、2.65 mm/d、3.23 mm/d;Ⅲ期间的变形速率为 1.33 mm/d、1.51 mm/d、1.99 mm/d。从中可以看出路堤断面对称轴附近的沉降速率为最大,选取测点3的变形速率作为竖向变形因子的初始值进行评价,即变形速率分别为 vⅠ=3.35 mm/d,vⅡ=3.23 mm/d,vⅢ=1.99 mm/d。
3.1.3 土压力数据分析
根据求得在Ⅰ期间1、2两测点的土压力变化速率分别为9.135 kPa/d、9.937 kPa/d;Ⅱ期间的土压力变化速率为11.775 kPa/d、14.218 kPa/d;Ⅲ期间的土压力变化速率为2.305 kPa/d、6.927 kPa/d。从中可以看出测点2的变化率较大,选取测点2的变化速率为土压力因子的初始值进行评价,即 vⅠ=9.937 kPa/d,vⅡ=14.218 kPa/d,vⅢ=6.927 kPa/d。
3.1.4 其他参数分析
通过对工程资料的分析和整理:确定边坡形态中第Ⅰ、Ⅱ、Ⅲ阶段末的坡高分别为13.5 m、16 m、18 m,坡角为30°;填料性质中的内摩擦角约为40°、黏聚力约为29 kPa。
3.2 突变级数值计算
由上文确定了各评价因子的初始值,下面以第Ⅰ阶段的路堤突变级数值计算做详细演示。侧向变形速率初始值vⅠ=1.56 mm/d,竖向位移速率初始值vⅠ=3.35 mm/d,土压力变化速率 vⅠ=9.937 kPa/d,坡高 HI=13.5 m,坡角 ψf=30°,黏聚力 c=29 kPa,内摩擦角φ=40°。
3.2.1 无量纲化计算
对于侧向变形速率、竖向位移速率、土压力变化速率进行无量纲化计算。通过综合分析并确定:侧向变形的区间界限值为x1=1.5 mm/d,x2=4 mm/d,x3=6 mm/d;竖向位移的区间界限值为x1=3 mm/d,x2=5 mm/d,x3=10 mm/d;土压力的区间界限值为x1=5 kPa/d,x2=15 kPa/d,x3=25 kPa/d。
侧向变形:

竖向位移:
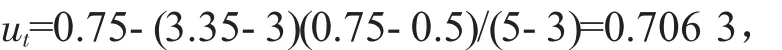
土压力:
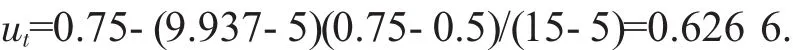
将坡高设为 HI、坡角设为 ψf、黏聚力设为 c、内摩擦角设为φ,分别对上述各量进行无量纲化计算。并综合分析确定:坡高界限值为x0=0 m,x1=5 m,x2=20 m,x3=40 m;坡角的界限值为 x0=0°,x1=30°,x2=35°,x3=45°;黏聚力的区间界限值为x0=40 kPa,x1=20 kPa,x2=10 kPa,x3=0 kPa;内摩擦角的界限值为 x0=50°,x1=30°,x2=20°,x3=10°。
坡高:
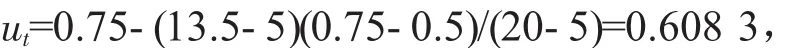
坡角:
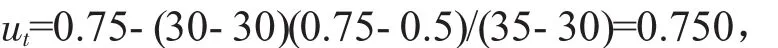
黏聚力:
内摩擦角:
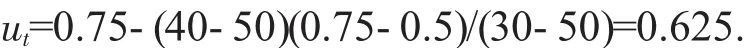
3.2.2 归一化计算
由前面分析可知侧向变形(B1)、竖向位移(B2)、土压力(B3)形成燕尾突变模型,坡高(D1)和坡角(D2)形成尖点突变模型,黏聚力(C1)、内摩擦角(C2)形成尖点突变模型,进行归一化计算。
对 于 B1、B2、B3有 :B1=0.7441/2=0.8625,B2=0.70631/3=0.891,B3=0.62661/4=0.8897,依据“非互补”原则,大中取小,即B=0.8625。
对 于 C1、C2有 :C1=0.60831/2=0.780,C2=0.751/3=0.9086,依据“非互补”原则,大中取小,即 C=0.780。
对 于 D1、D2有 :D1=0.88751/2=0.9421,D2=0.62501/3=0.7906,依据“非互补”原则,大中取小,即D=0.7906。。
对于构成燕尾突变模型B、C、D采用燕尾突变的归一公式:B=0.86251/2=0.9187,C=0.781/3=0.9205,D=0.79061/4=0.9430。依据之前提出的非互补时大中取小的原则,AI=0.9205,即路堤第Ⅰ阶段的总突变函数值为0.9205。
同上可求路堤第Ⅱ阶段的总突变函数的函数值为0.9083,第Ⅲ阶段的总突变函数的函数值为0.8718。
3.3 结果评价
从这3个阶段突变值的大小可以看出,施工期路堤的突变值逐渐变小,这说明路堤的安全稳定性在路堤施工的中后期要小于前期施工时。但是各阶段的突变值均较大,且现场路堤施工期安全良好,没有产生滑坡或大裂缝。根据本文的计算方法和界限值的选取,将突变级数值与路堤安全状态进行分级划分,分级标准见表2,可依据该准则对高填方路堤存在的安全风险进行评价。通过对其他断面监测数据的计算分析,突变级数值在0.86~0.93之间,说明本次监测的路堤工程在施工过程中安全性良好,风险等级为Ⅰ级的低风险区域。

表2 高填方路堤施工期安全风险评价表
4 结论
a)将现场监测数据通过突变级数理论进行理论分析与论证,得出了在施工期的高填方路堤安全风险评价模型。确定了侧向变形、竖向位移、土压力、坡高、坡角、黏聚力、内摩擦角等因素为模型的主要评价因子。
b)以突变级数为理论基础,确定了高填方路堤在施工过程中的风险等级标准为:Ⅰ安全,Ⅱ一般安全,Ⅲ不安全。计算得到了监测路堤在施工期不同阶段的突变级数,实现了对路堤施工期各阶段的风险评价。通过对路堤施工期变形与稳定性的有限元分析,表明本文监测方案及突变级数风险评价在高填方路堤施工期风险评价的合理性。
