例谈小学英语复习课的教学

任艳

Lesh 提出与数学学习有关的五种表征，即“实物、教具模型、图形、语言与符号，其中前三个表征较为具体，后二个表征较为抽象”[1]。用画图方式呈现问题，或在文字题上附加图画，是教科书及实践中教师经常采用的一种解题表征方式，这种以视觉手段表征知识的方式，即称之为可视化表征，它能将文字题当中的数量关系可视化、具体化。Van Hiele认为，利用可视化的表征方法有降低思考层次的效果[2]。在小学高年级阶段，许多问题都是以文字的形式来表征的，因其较为抽象，大多数学生尚停留在具体思维阶段，问题理解存在一定的困难，而线段图表征具有内在负荷相对较低的特点，因此成为利用可视化表征解题的良好载体。笔者以线段图为例，提出运用可视化表征的文字与图形整合的教学模式，即把问题情境以线段图示表现出来，通过线段图辅助学生建立一个数量关系的心智模式，进而克服文字阅读的困难，降低学生理解问题的思维负荷，增加其在“问题解决”的过程中体验成功的机会。

一、作线段图表征问题

教材中的例题和习题，一般鲜有明确给出线段图的。线段图有两种表征方式：无单位的线段图和有单位的线段图。研究所指的线段图是有单位的线段图，即用二条线段表示题目中各个数量间的关系。教学实践中，当学生阅读题目文字时，可能无法理解题目所描述的数量关系，因而难以建立一个适当的心智模式，而线段图作为外部表征可以尝试引导学生去建立此数量关系的心智模式。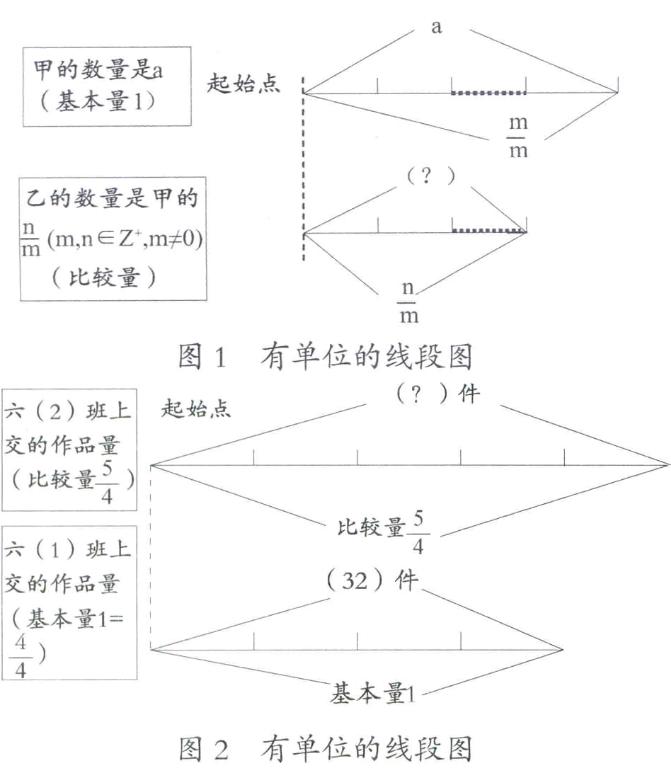

当个体面临问题时，会在脑海中或在纸上呈现与问题有关的图像，以帮助个体进行解题思路的可视化表征[3]。关于线段图表征，教学中应给学生厘清：图中每一条线段表示什么；线段的单位数量能否体现出问题中各个量的数量关系。线段图表征方式具体，而且易于体现数量间的倍数或比例关系。如图1所示。

在小学阶段，遇到难度较高的分数问题（例如分数乘法、除法、异分母分数加减等问题）时，适宜引入线段图来表征这些问题，它可以有效地消解因过多的元素互动造成认知负荷过大的情形。另外，用单位长度表征可以进行多次的具体等分及合并活动，实践中可保留这些活动的痕迹，其优点在于：一方面，这些具体操作活动是进一步抽象思考的基础，另一方面，保留具体活动痕迹更易于监控解题过程及反思解题过程。

二、确定基本量与比较量，找出（计算）比例关系

线段图表征需要先确定一个元素作为单位，然后以该单位作为新的测量标准，此单位即基本量，再以基本量来诠释别的元素，即比较量。表征问题情境的线段图用基本量来刻画，即线段图的单位。

三、依据比较量与基本量的比例关系，画出二条并排线段图

学生对文字信息进行语意处理，一般情况下，都需要纳入长时记忆区中的认知结构来理解，即以其已有的认知结构为基础。但是在问题解决的特有情境下，学生可能不能及时触发其适当的认知结构来进行概念组织。因此，需要对问题中的文字叙述进行恰当的命题表征来辅助学生建构心智表征，进而促进学生理解题意。

对于小学高年级学生而言，均已具备一定的空间意义和认知体验。因此，可采用可视化的线段图表征命题，以直观的线段图来表征元素间的相互关系。表征的意义在于利用学生长时记忆区中的认知结构引导其进行模式建构与模式识别的活动。模式建构是指利用线段图来表征两个班级上交作品数量的大小关系，模式识别是指这两条并排的线段能否恰当地表现两个班级上交的作品的数量关系。因此，可画起始点相同、二条并排的线段图，即描绘性表征，以此来比较两个量之间的相互关系。

两个班级上交作品的数量间关系不仅可以用来分析文字与图象的理解，也可以用来研究从外部表征——可视化的线段图表征来建构内部表征——心智表征的过程。这种外部表征可以用来沟通、分享知识的习得，如实践中教师会通过线段图来辅助讲解题意，学生也可将产生的外部表征视为认知工具来辅助问题解决，即可以依托线段图载体思考两个量之间的相互关系，同时将问题解决过程中所需的认知需求反映到线段图当中。

四、依据线段图，列式解决问题

在画线段图的过程中，线段图表征与心智模式会持续地产生交互作用，进而促使学生对文字和图象所要表达的意义理解得更清晰、更深入，并在理解的过程中不断修正和完善学生建构的心智模式与命题表征。如引导其认知结构进行模式检测——线段图能否准确体现文字表达的数量关系。学生在描述性表征和描绘性表征的互动过程中，借助线段图的辅助，完善心智表征，提取有效信息，正确列式，进而正确解决问题。

六（1）班上交作品为基本量时，数量是32，每个单位格是32÷4=8 （件），六（2）班上交作品量是8×5=40 （件）。所以两个班级一共上交作品：32+40=72 （件）

答：两个班级一共上交作品72件。

线段图作为一种常规的可视化表征手段，教师引入其表征解题策略的目的不仅仅是解题，更多的因素是期待学生能够理解表征背后所表达的关系，进而从表征所建立的模式中提取出新的信息，以此实现问题解决的目的。

值得一提的是，教学模式中元素间的关系通常是以“比较量÷基本量=比值”来表达，即“比与比例”。现今各版本的小学数学教科书中，对“比与比例”内容，采取不同的呈现方式和逻辑结构，教师可将线段图作为理解分数解法的辅助工具，让学困生也能掌握整数乘除与分数乘除解法之间的关系，提升学生在“比与比例”单元学习成功的机会。

总之，可视化表征可以使得研究内容更直观化、关系更具体而清晰，而且能够“帮助他人正确地重构、记忆和应用知识”[4]。可视化的线段图表征目的在于把问题情境以可视化的方式表征出来，并通过线段图提升学生的列式和运算能力。因此，可视化表征是辅助学生“怎样解题”的一种有效而且高效的教学工具。

参考文献

[1] Grouws D A.Handbook of Research on Mathematics Teaching and Learning[M]. New York：Macmillan Publish Company，1992.

[2] Van Hiele，P.M.Structure and insight[M].New York：Academic Press，1986.

[3] 王寬明.可视化表征在工程问题中的应用[J].教学与管理：小学版，2016（3）.

[4] 邱杨，高荣国.以知识可视化表征改善学习内容的呈现[J].江苏教育学院报，2007，24（4）.

[责任编辑：陈国庆]endprint