平行四边形的判定的拓展
2017-10-25李焕兰


我们知道平行四边形具有以下性质:
①对边平行;②对边相等 ;③对角相等;④一条对角线平分另一条对角线;将①②③④两两组合在一起(包括①①、②②、③③、④④)作为条件,可构成如下关于判断四边形是否是平行四边形的12个命题:
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形。
(4)两条对角线互相平分的四边形是平行四边形
(5)一组对边平行且相等的四边形是平行四边形。
(6)一组对边平行,一组对角相等的四边形是平行四边形
(7)一组对边平行,一条对角线平分另一条对角线的四边形是平行四边
(8)一组对角相等且连结这组对角顶点所得对角线平分另一条对角线,这样的四边形是平行四边形。
(9)一组对边平行,另一组对边相等的四边形是平行四边形。
(10)一组对边相等,一组对角相等的四边形是平行四边形。
(11)一组对边相等,一条对角线平分另一条对角线的四边形。
(12)一组对角相等且连结这组对角顶点所得的对角线被另一条对角线所平分,这样的四边形是平行四边形。
下面我们来探讨以上命题,哪些是真命题,哪些是假命题,若通过证明是真命题,即可作为判定四边形是平行四边形的一种方法;若能举出反例或画出反例图,则说明是假命题;在今后遇到这类情况能准确判断真伪、不至于混淆出错。
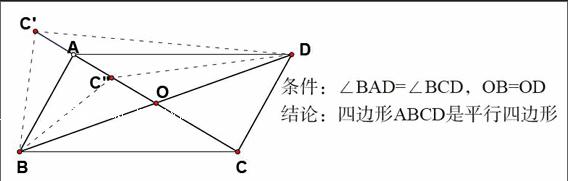
1.显然,(1)至(5)是课本上的定义或证明了的定理,它们是真命题,我们在这里就不赘述了,也易证(6)和(7)是真命题,而(8)也是真命题,但学生用现有的方法不易证明,我们可用同一法的思想来说明:如图,
将四边形绕O点旋转180°,使B 點与 D点重合,若C点 与A点不重合,则会落在C′或C″处,此时∠B C′D﹤∠BAD 或 ∠B C ″D﹥∠BAD(三角形的外角大于不相邻的两内角和),故C只能落在A处,即OA=OC,由此说明四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).
2.(9)至(12)是假命题,下面我们就举出反例并画出反例图命题(9)反例图
(10)图
(11)
(12)
综上所述:判断一个四边形是否是平行四边形的情形还有三种,即上述探讨论证了的真命题(6),真命题(7),真命题(8),虽课本中没把它们作为定理出现,但探究的过程和结论可拓宽我们的视野,提高我们识别和应变能力,同时也可快而准应对测试中有关平行四边形的选择和判断类型习题。
作者简介
李焕兰(1964.2-),女,汉族,湖北,中学高级教师,武汉市中学数学学科带头人,中国数学奥林匹克一级教研员,武汉大学数学专业研究生毕业,武汉外国语学校教师,从教多年来,关注数学教学的改革和学生的思维训练,致力于中学高效课堂、中学生数学心里健康、中考数学、中学奥林匹克数学的研究endprint
