“五点一线，攀扶而行”

朱红雅

【摘要】 数学概念是反映数学对象的本质属性的思维形式。在中职数学教学中强化概念教学，教师要把概念的形成当作“多点一线”的一种逻辑过程，适时地进行帮扶，引导学生自主攀升，实现中职数学教学的轻负高效。

【关键词】 中职数学 概念教学 有效性 点线结合

【中图分类号】 G712 【文献标识码】 A 【文章编号】 1992-7711（2017）09-094-02

0

对于极大多数中职学生而言，由于在义务教育的某个时间段出现对数学概念的忽视与不理解，导致了数学成绩急剧下降，最终引发数学学习的“灭顶之灾”。数学概念是反映数学对象的本质属性的思维形式，是数学思想与方法运用的载体，是数学学习“绕不过的弯”。在中职学校数学教学中强化概念教学，打造适合学生的概念课，是缓解中职生数学学习困境的不二法门。

一、瞄准起点，有效引领

中职数学概念教学必须准确定位学生的学习起点，遵循中职生数学学习的基本认知规律。

1. 从生活起点引入概念

数学概念是对生活中某类事物本质属性的概括，但学生也不可能是完全”一张白纸“的形式进入学习的，而且不少学生早已经建立了相关的前概念。比如“椭圆”这一概念，有学生认为鸡蛋的形状是“椭圆”的，有学生认为把一个圆形的铅丝圈拉扁，此时铅丝就组成一个“椭圆”。上课时笔者先用多媒体给学生呈现了各种表面是椭圆形的物体，然后从这一些物体表面中抽象出其共同的特性。然后我让学生借助课前准备好的学具进行动手操作：用一条固定长度的线，把线的两端固定在画图板的两个钉子上，然后让铅笔保持在线上进行作画，从而引出椭圆的概念。这样既避免了静态文字引入带来的枯燥乏味，而且于学生的生活前概念密切相连，使学生认识到了生活与数学的联系与区别，升华了概念。

2. 联系逻辑认识起点引入概念

逻辑起点是指特定概念在教学体系中的学习基础。例如，学生学习“指数函数”这一概念的起点是“函数”概念，最近的起点概念是“幂函数”。在教学时，要充分以学生对“幂函数”这一概念的理解为起点，让学生先回顾“幂函数”是如何定义的。学生都知道在幂函数M=ab中，b是固定不变。而a是能在一定范围内变化，教学可以引导学生这样思考：在M=ab中是不是可以固定a不变，而让b在一定范围内变化呢？如果可以M也有一个唯一的值与之对应，也构成一个函数。于是，我们可以这样引入指数函数，用x和y来代替b和M，这样得到y=ax，由于这时的自变量处于指数位置，我们称这种函数为指数函数。“温故而知新”，其实很在程度上需要抓住数学概念间的逻辑联系，让旧概念的复习成为新概念学习的有效起点。

二、借力疑点，激趣动情

以生活化的问题为基础，注重挖掘中职学生的兴趣点与疑点，将有效促进概念理解的主动性有效性。以“待定系数法”为例，虽然不少学生在初中时已经掌握，但由于其操作步骤比较复杂，很多学生早已经忘得一干二净，于是我在学生学习指数函数时出示了以下习题：

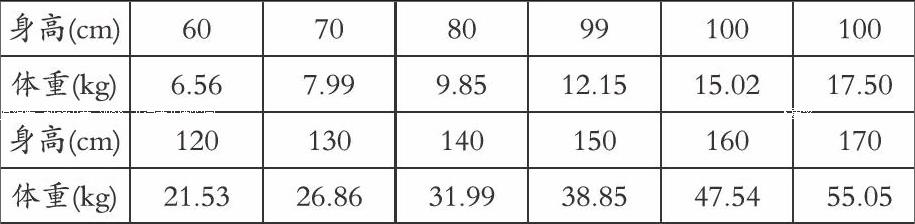
2015年绍兴市中职男生的身高与体重平均值统计如下。

（1）请画草图分析两个变量的图象与什么函数比较相像。

（2）如果绍兴市中职男生身高（x）与体重（y）之间的函数关系式为y=axk（a>o，a≠1），那么你能确定该关系式中a与k的值吗？

第一小题，学生通过草图描点很快锁定该函数图像与指数函数相似，但到了第二小题时，除了基础稍好的学生知道解决的办法外，极大部分学生仍然一筹莫展，于是我问学生：函数y=axk中哪些是常数，哪个是自变量，哪个是应变量，现在我们要确定的是什么量？用什么方法解決？学生很快就明白了要确定的是常数，这种确定常数的方法就是待定系数法。

怎么样运用待定系数法确定常数呢？我让一个学生回答，然后大家参与计算，最终将表格中的两对自变量与应变量的对应值代入得到了a≈1.02，k≈2.自此，学生这种方法有了较清晰的认识。然后我又问：你的身高是多少，你知道自己与中职生平均体重比较是偏重还是偏轻吗？有学生从表格中去估算，但这不科学，用什么方法好呢？我又引导：现在已经确定了函数的常数，又知道了函数的自变量（身高），大家可以求出函数的什么？到后来，班级里非常热闹，有的还不断发出嬉笑声，他们对自己的体重与同身高中职生的平均体重之间有了一个比较，不少同学甚至感觉不好意思了，表示要进行减肥。

三、打造热点，驾驭心灵

概念有名称、定义、属性三个要素，学生能脱离书本用自己的语言准确地叙述它，这是概念形成的重要标准，在这个过程中要让学生自主探究，在体验中促进思维发展。

例如，“异面直线所成的角”一课，教学时可以这样引导学生在自主探究的过程中形成概念。

（1）问题：怎样刻划异面直线间的相对位置？

（2）提示：两条异面直线分别为a、b，a、b不相交，但这两条直线之间存在一个倾斜程度不同的角来衡量它们之间的倾斜程度。

（3）猜想：能不能把两条异面直线a、b的倾斜程度转化为平面内两条相交直线的角呢？

（4）探究：得出两异面直线所成角的范围及相关的规律。经过这样的猜想、探究，两异面直线所成角的概念就能建立起来。

可见，数学概念的形成过程一定要让学生进行自主探究，要紧紧围绕学生富有创造性的“猜想——验证——发现”的学习过程，才能让学生在不断探究孕育新的数学概念的形成。

四、定位落点，经纬分明

利用概念图加深数学概念理解。在概念的深化阶段，教师要引导学生根据数学概念的内涵和外延进行概念图的绘制，例如，在教学“二次函数”这一概念时，在概念的深化阶段，笔者组织学生对二次函数的相关知识进行整理，并在此基础上让学生根据二次函数概念的内涵和外延绘制概念图。课堂上，学生绘制的数学概念图包含了二次函数表达式的三种形式，实现了三者之间的有机联系和纵向拓展。这样，学生就能够在画概念图的过程中对数学概念加深理解。endprint

有些数学概念之间是存在紧密联系的，因此，在数学概念的深化阶段，教师要善于引导学生把新学的概念与原有的概念之间进行前后联系，并画出数学概念图。比如一元二次方程、一元二次不等式与二次函数之间的平行对等关系。具体如二次函数y=ax2+bx+c图象在什么时候与x轴有两个交点、只有一个交点、没有交点，这个问题与一元二次方程求根公式中的Δ之间的关系又是什么，对于这些问题的深究必将使数学知识形成框架与网络，很多问题可以触类旁通、举一反三。

五、挖掘基点，精益求精

概念的内涵和外延是概念的基本属性，也是概念教学的基点。比如，教学“集合”这一概念之后，为了让学生能够对这一数学概念有更加深入的理解与把握，可以引导学生进行数学应用：（1）全班的男生能不能构成一个集合？（2）A={中国，美国}，B={USA，China}，A和B是不是同一个集合？（3）中国目前为至已经获得诺贝尔物理学奖的所有国内学者能否组成一个集合？对于第（1）题，对照定义——集合是指具有某种特定性质的的对象汇总成的集体，而全班男生正是在全班学生中具有男性特征的那部分学生的集体，所以全班男生能够构成一个集合。很明显，这一小题是针对集合的内涵来提问。而第（2）小题，全面考察概念的内涵——同一集合中的对象的集体是一个总的概念，所以不必考察顺序，用不同的语言来表达几个相同的对象，只是形式的不同，但其实质是一致的，所以A=B。第（3）小题则进一步深入探讨集合的外延，因为集合有多种形式：比如某集合的子集也是集合，空集也是集合，而这里所说的”目前已经获物理学诺贝尔将的中国学者“其实是一个空集，所以也构成一个集合。可见，对于概念的辨别需要通过实际应用才能深化与理解，而且要紧紧围绕概念的基本属性来展开，“既不少一丝，也不多一分”，使学生能将概念的内涵与外延在头脑中建立牢固的链接。

综上所述，数学概念是中职数学教学的重中之重，它既是复习初中数学的重要落脚点，也是升华中职数学教学的敲门砖。在中职数学概念教学中，教师要根据教学内容与中职生的实际特点，把概念的形成当作由上述五个点组成的一种逻辑过程，贯穿起概念教学的一条纵线，通过教师帮扶引导学生自主攀升，既使教学过程能“探之有趣，究之有果”，又可實现中职数学教学的轻负高效。

[ 参 考 文 献 ]

[1]喻平.《数学教育心理学》[M].广西教育出版社，2004.

[2]加里·D·鲍里奇（美）.《有效教学方法》[M].江苏教育出版社，2008.

[3]王晓霞.中职数学概念教学要关注“三个点”[J].内蒙古教育，2014（08）.

[4]牟正道，叶思义.《数学（基础模块）上册》[M].人民教育出版社，2009.endprint