烟杆废物热解动力学研究
2017-10-24务文涛李志华赵贝贝
务文涛, 李志华, 赵贝贝
(1. 广西中烟工业有限责任公司, 广西 南宁 530001; 2. 广西区烟草公司, 广西 南宁 530001)
·研究报告—生物质能源·
烟杆废物热解动力学研究
务文涛1, 李志华1, 赵贝贝2 *
(1. 广西中烟工业有限责任公司, 广西 南宁 530001; 2. 广西区烟草公司, 广西 南宁 530001)
通过热重分析(TGA)方法,采用单步和三平行反应模型分别考察烟杆废物的热解动力学。烟杆废物单步热解的平均活化能为182.4 kJ/mol,最适宜的反应机理函数为14级反应机理f(α)=(1-α)14。能量补偿效应结果显示烟杆废物的热解可以分为3个阶段α=0~0.32、α=0.32~0.80和α=0.80~1,各阶段的指前因子分别为2.88×1010、4.33×1014和9.76×1016s-1。单步热解过程中伴有表观活化能的变化以及高级数反应的机理,不能合理地描述烟杆废物的热解机理。采用混合韦伯分布活化能模型考察了三平行反应热解动力学,结果显示:混合韦伯分布活化能模型能很好地拟合烟杆废物热解数据,相关系数R2≥0.997 6;3种伪组分的活化能大小符合E0(木质素, 195.26 kJ/mol)>E0(纤维素, 152.54 kJ/mol)>E0(半纤维素, 121.18 kJ/mol)的顺序;半纤维素的热解机理为一级反应f(α)=1-α,纤维素的热解机理属于成核机理,木质素的机理亦呈现级数反应,级数介于n=3~4之间,木质素的热解机理复杂,可能为多步反应。
烟杆废物;热重分析;热解动力学;韦伯分布
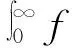
1 实 验
1.1材料
烟杆废物取自贵州省毕节市某农村,经过晒干(15d)、破碎、磨碎、筛分后得到粒径<0.165 mm的粉末,备用。烟杆废物样品的元素分析由元素分析仪(Vario Micro cube, Elementar)测定,工业分析按照国标GB/T 212—2008测定,低位热值(QLHV)通过氧弹热量计测得,结果见表1。

表1 烟杆废物的元素分析及工业分析结果
1.2热重分析实验
烟杆废物的TGA实验在热重/差热同步分析仪(SDT Q600,TA Instrument,USA)上进行。实验的样品量控制在5~10 mg[13],以高纯氮气(80 mL/min)作为吹扫气以保证绝氧热解气氛,样品从室温以10、20和30 ℃/min的加热速率加热至750 ℃。由于在高温阶段会出现焦油和气体与半焦的二次反应[21],因此本研究考察烟杆热解动力学时的温度范围取105~700 ℃。
1.3热解动力学模型
1.3.1单步反应 单步反应模型通常结合等转化率法和主曲线法(Master-plots)确定动力学参数和机理函数。线性非等温加热程序的TGA实验中,固相材料热分解的单步反应表观动力学方程为:
dα/dT=A/βexp(-E/RT)f(α)
(1)
式中:R—普适气体常数,8.314 J/(mol·K);A—指前因子,s-1;E—表观活化能,J/mol;β—加热速率,K/s;f(α)—机理函数(常见形式如表2所示) ;α—转化率,%;T—温度,K。
α的计算公式见式(2):
α=(m0-m)/(m0-mf)
(2)
式中:m0、m、mf—起始温度、任一温度和终止温度对应的标准化质量,%。

(3)
(4)
式(4)的k为第k个加热速率;采用多个加热速率(一般为3~5个),用式(4)左边对-1/Tα,k作图得一直线,其斜率可计算活化能(Eα)。机理函数f(α)或g(α)可根据最大归一主曲线法确定[23]:
y(α)=(dα/dT)α,Expexp(E0/RT)=A0f(α)The
(5)
式(5)中y(α)为主曲线函数;E0为KAS方法中Eα的平均值;下标Exp和The分别代表实验值和理论值。将y(α)函数值归一至相应的最大值,表示为:
y(α)norm=y(α)/max[y(α)]
(6)
以y(α) 对α作曲线,实验曲线越接近表2的理论曲线即说明烟杆单步热解越符合这一模型。根据已知的E0和f(α)(即g(α)已知),从式(4)线性回归的截距可以求出Aα:
(7)
式中:I—截距值。
1.3.2混合韦伯分布活化能模型的三平行反应 分布活化能模型(DAEM)认为单步反应中包含无穷多个不可逆的一级反应g(α)=-ln(1-α),活化能为连续的概率密度分布函数f(E),此时单步反应的α和T与f(E)的关系式表示为:

(8)
令f(E)服从韦伯分布(式(9))即为韦伯分布活化能模型。
(9)
κ(κ>0,无量纲)和λ(λ>0, J/mol)分别为Weibull分布的形状参数和尺度参数;Es(J/mol)代表特征活化能或活化能分布的位置参数,对应的平均活化能(E0)可用Gamma函数Γ(x)表示为:
E0=Es+λΓ(+1/κ)
(10)
对于烟杆废物热解的混合Weibull分布活化能模型,失重速率表示为:
(11)
式(11)的i代表第i组分;ci为第i组分对总失重速率的贡献分率,0 (12) 式中:S—方差;OF—目标函数;p—混合韦伯分布活化能模型中未知参数的总数,为15。 方差(或OF)越小优化结果越好,S<5 %说明模型对实验数据的吻合程度显著。烟杆废物热解经混合Weibull分布活化能模型优化后,可得到伪组分的失重速率曲线(dα/dT),其热解机理函数可通过单步反应模型中的主曲线法进一步确定。 1.3.3常见的热解机理 在固体热分解动力学研究中,适用于单步反应模型的具有明确物理化学意义的机理函数见表2。 表2 固相材料热分解常用机理模型 2.1烟杆废物热解特性 图1为烟杆废物不同加热速率下的热重分析结果。从图中可见,室温至150 ℃区域内大约有10 %的失重,由水分和轻质挥发分(乙酸、乙醇等)挥发导致。温度继续上升至300 ℃左右,DTG曲线出现肩部,根据TPR模型,该肩部主要由半纤维素分解速度达到最大后与纤维素分解的DTG曲线发生重叠造成[24]。温度达到约325~350 ℃,DTG出现最速分解峰,由纤维素的快速热解引起。纤维素可认为是晶体,达到某一温度后即可快速完成分解并在峰的右侧形成陡坡。在陡坡出现后,烟杆的失重速率趋于缓慢,形成拖尾,主要是由含苯环结构、热稳定性强的木质素组分分解所贡献[24]。 图1 烟杆不同加热速率下热重分析方法结果Fig. 1 TGA results of tobacco stem pyrolysis under different heating rates 从反应速率曲线dα/dT可见(图1(c)),肩部、峰和拖尾起始点对应的特征温度随着加热速率的增大而升高,是由加热速率主导下的热滞后引起的加热速率的升高使得样品表面到达同一温度的时间减小,但传热使样品中心到达该温度所需的时间缩短,从而使得热解时间缩短而最大失重速率滞后。 2.2烟杆废物单步热解动力学 2.2.1KAS等转化率法 图2为几个特征转化率下的线性拟合及α=0.04~0.96时拟合方程的回归相关系数R2。图中显示,低转化率(α=0.04~0.08)及高转化率(α=0.84~0.94)对应的R2值均较差,低于0.96,说明此区域内计算得到的活化能并不准确。 图2 KAS拟合图及其相关系数值Fig. 2 Fitting schematic diagram of KAS method and its R2 图3 活化能(Eα)及Eα和E0的相对误差的转化率依赖性Fig. 3 Dependancies of Eα and the relative error of Eα and E0 versus α 图3显示Eα随转化率的变化较大,从最小的169.9 kJ/mol(α=0.62)增加到最大的450.0 kJ/mol。最大Eα值对平均值(E0=213.1 kJ/mol)产生的相对误差约为90 %,远远大于单步反应模型活化能偏差低于30 %的上限(一般来说,最大或最小活化能对平均值相对误差大于30 %时,即可认为热分解是多步反应而非单步反应[13]),说明单步反应模型并不适用于生物质热解。同时,图3中Eα随α的变化趋势非常复杂,在α=0.40~0.62之间甚至出现活化能下降趋势。活化能Eα出现下降时,说明单步反应其实发生了反应机理的变化[11],而机理的变化并不能够从简单的Eα下降趋势确定[24]。 2.2.2单步反应机理 将标准偏差大于30 %的Eα忽略,计算得烟杆废物单步热解的平均活化能为E0=182.4 kJ/mol,代入式(5)和(6)得到的最大归一主曲线图形如图4所示。从中可见,在低转化率处实验的y(α)norm曲线与表2中的扩散模型(D1、D2、D3、D4)一致,可能是由结合水及提取物通过扩散首先析出造成。而随着转化率升高,y(α)norm曲线与扩散机制D3最接近,但仍偏离较远,采用高级数的级数反应机理进行推算,发现n=14时的14级反应与实验数据取得良好吻合,与Ceylan等[25]和Damartzis等[26]所得的n=9和n=12的高级数机理结果相近,因此最佳的机理函数为级数反应f(α)=(1-α)14。 2.2.3单步反应指前因子 根据能量补偿效应,lnAα对Eα作图为直线: lnAα=aEα+b (13) 其中,a,b为常数。求得a和b后,A0可代入下式求得: lnA0=aE0+b (14) 从图5的lnAα对Eα的线性回归图可见,热解过程的lnAα与Eα的线性关系极差,但明显可以分出3个线性关系很好的阶段,分别对应于α=0.06~0.32、0.32~0.80和0.80~0.94,各阶段的指前因子分别为2.88×1010、 4.33×1014和9.76×1016s-1。根据能量补偿效应,对于单步反应模型来说,lnAα和Eα应当具有良好的线性关系,然而热解过程在整个转化率区间内lnAα和Eα的线性关系很差,因此,烟杆不是按照单步反应进行热解。 图4 最大归一主曲线图Fig. 4 Maximum normarized Master-plots 图5 能量补偿效应Fig. 5 Energy compensation effect plots 2.3混合韦伯分布活化能模型的三平行反应动力学 烟杆废物热解的混合韦伯DAEM的计算通过优化目标函数(式(12))得到,本研究采用MATLAB中的patternsearch全局优化工具实现目标函数的最小化,其中模型和实验的-dm/dT的值通过数值微分(差分方法)得到,计算结果见表3。图6给出了计算结果和实验的对比情况,从中可见,混合韦伯DAEM与实验值取得非常好的吻合,其中方差S=1.13 %,R2≥0.997 6。3种伪组分的活化能大小符合TPR模型中的排列顺序:E0(半纤维素) 表3 烟杆废物热解混合韦伯DAEM计算结果 图6 烟杆废物热解混合Weibull拟合图Fig. 6 Calculated results of tobacco stem pyrolysis according to the mixture Weibull DAEM 将表中Es、λ和κ值代入公式(9)得到伪组分热解活化能的韦伯分布,结果见图7。从活化能分布的宽度可看出木质素的宽度最大,其次为半纤维素,最小为纤维素(κ=6.46),这一结果与对称分布的高斯分布取得一致[19]。纤维素活化能分布之所以最小,是由其结构及热分解特性决定的,纤维素一般认为是一种晶体,一旦达到某一温度即可快速分解[24],形成其DTG曲线峰右部的陡坡,从而主要贡献于样品DTG曲线的陡坡,如图6所示。 图7 伪组分活化能Weibull分布Fig. 7 Weibull distribution of activation energy for pseudo components 2.4伪组分热解机理 由混合韦伯分布DAEM计算得到的伪组分的E0和A后得到g(α)值,通过式(15)进行半衰期(α=0.5)归一处理,对照表2考察其热解机理,结果如图8所示。 (15) 从图8(a)可见,半纤维素的热解机理与级数反应最接近,介于n=1和n=2之间。然而,化学级数反应机理在固相中并没有物理化学意义,可以解释为成核反应现象,即级数n相当于半纤维素在热解过程中首先形成核子,核心的生长其实按照均相反应的碰撞逐渐增大[27]。 图8 伪组分的热解机理 图8(c)显示木质素的热解反应级数于n=3~4之间。按照碰撞态理论,n=3的反应极难出现,因此木质素按照级数反应机理解释并不合理。有研究表明,木质素的热解过程分为2步:第一步首先是苯环支链断裂,第二步是第一步的产物继续分解[28]。第二步涉及到苯环及其化学活性弱的支链断裂,需要较高温度才能有明显失重。这说明木质素的热解可能机理非常复杂,可能为多步反应。 至于纤维素,从图8(b)可见其机理属于成核机理(A2),与Burnham 等[29]的结果一致。但Burnham等指出纯纤维素热解的表观活化能为191~253 kJ/mol,本研究结果(E0=152.54 kJ/mol-1)与这一结果相差甚远。对此活化能差异,Burnham等认为E0是由热解过程中H2O的催化作用或附近的OH基造成。另外,Anca-Couce等[14]认为,灰分中的金属元素亦对热解起催化作用,降低了活化能。 3.1通过热重分析研究了烟杆废物的热解动力学,结果表明,单步反应模型中,烟杆的表观活化能随转化率的变化大,最大活化能值对平均值的相对偏差超过30 %;最佳的机理函数为级数反应f(α)=(1-α)14;根据能量补偿效应,烟杆的热解分为3个阶段。单步反应模型不适合描述烟杆的热解机理。 3.2采用混合韦伯分布活化能模型考察了烟杆的三平行模型(TPR),结果显示:混合韦伯分布活化能模型能对实验数据取得很好的拟合效果,相关系数R2≥0.997 6;伪组分的活化能大小符合E0(木质素)>E0(纤维素)>E0(半纤维素);半纤维素的热解机理为一级反应f(α)=1-α,纤维素的热解为成核机理;木质素的机理为级数反应,级数介于3~4之间,热解机理复杂,可能为多步反应。 [1]陆炳,孔少飞,韩斌,等. 2007 年中国大陆地区生物质燃烧排放污染物清单[J]. 中国环境科学,2011,31(2):186>-194. [2]张承龙. 烟杆的资源化利用技术现状及其前景[J]. 可再生资源研究,2002(1):38>-39. [3]李黎,李清海,蒙爱红,等. 烟杆热解固体产物性质及其影响因素研究[J]. 可再生能源,2011,29(6):106>-109. [4]樊雪志. 中国烟草农业的发展现状及趋势分析[EB/OL]. 2014-01-02. http://www.tobaccochina.com/tobaccoleaf/roundup/update/20141/20131231152416_600622.shtm. [5]杜海清,白雪峰. 生物质热解技术研究进展[J]. 生物质化学工程,2007,41(4):54>-58. [6]胡强,陈应泉,杨海平,等. 温度对烟杆热解炭、气、油联产特性的影响[J]. 中国电机工程学报,2013,33(26):54>-59. [7]张利波. 烟杆基活性炭的制备及吸附处理重金属废水的研究[D]. 昆明:昆明理工大学博士学位论文,2007. [8]李军,李吉昌,吴晓华,等. 烟草废弃物利用研究[J]. 雲南化工,2010,37(2):44>-49. [9]谭非,王彬元,林金春,等. 微波加热化学活化法制备活性炭的优化工艺研究[J]. 生物质化学工程,2010,44(1):1>-4. [10]夏笑虹,石磊,何月德,等. 炭化温度对烟杆基活性炭孔结构及电化学性能的影响研究[J]. 化学学报,2011,69(21):2627>-2631. [11]夏洪应,彭金辉,张利波,等. 二氧化碳活化制备烟杆基颗粒活性炭的研究[J]. 黄金,2006,27(7):38>-41. [12]WHITE J E,CATALLO W J,LEGENDRE B L. Biomass pyrolysis kinetics: A comparative critical review with relevant agricultural residue case studies[J]. Journal of Analytical and Applied Pyrolysis,2011,91(1):1>-33. [13]VYAZOVKIN S,BURNHAM A K,CRIADO J M,et al. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data[J]. Thermochimica Acta,2011,520(1):1>-19. [14]ANCA-COUCE A,BERGER A,ZOBEL N. How to determine consistent biomass pyrolysis kinetics in a parallel reaction scheme[J]. Fuel,2014,123:230>-240. [15]PEREZ-MAQUEDA L A,SANCHEZ-JIMENEZ P E,PEREJON A,et al. Scission kinetic model for the prediction of polymer pyrolysis curves from chain structure[J]. Polymer Testing,2014,37:1>-5. [16]CAI J,WU W,LIU R,et al. A distributed activation energy model for the pyrolysis of lignocellulosic biomass[J]. Green Chemistry,2013,15(5):1331>-1340. [17]SARVARAMINI A,ASSIMA G P,LARACHI F. Dry torrefaction of biomass-torrefied products and torrefaction kinetics using the distributed activation energy model[J]. Chemical Engineering Journal,2013,229:498>-507. [18]LAKSHMANAN C C,WHITE N. A new distributed activation energy model using Weibull distribution for the representation of complex kinetics[J]. Energy & Fuels,1994,8(6):1158>-1167. [19]CAI J M,LIU R H. Parametric study of the nonisothermal n th-order distributed activation energy model involved the Weibull distribution for biomass pyrolysis[J]. Journal of Thermal Analysis and Calorimetry,2007,89(3):971>-975. [20]JIANG G,NOWAKOWSKI D J,BRIDGWATER A V. A systematic study of the kinetics of lignin pyrolysis[J]. Thermochimica Acta,2010,498(1):61>-66. [21]RATH J,WOLFINGER M G,STEINER G,et al. Heat of wood pyrolysis[J]. Fuel,2003,82(1):81>-91. [22]STARINK M J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods[J]. Thermochimica Acta,2003,404(1):163>-176. [23]HU M,CHEN Z,GUO D,et al. Thermogravimetric study on pyrolysis kinetics ofChlorellapyrenoidosaand bloom-forming cyanobacteria[J]. Bioresource Technology,2015,177:41>-50. [24]HU M,CHEN Z,WANG S,et al. Thermogravimetric kinetics of lignocellulosic biomass slow pyrolysis using distributed activation energy model, Fraser-Suzuki deconvolution, and iso-conversional method[J]. Energy Conversion and Management,2016,118:1>-11. [25]CEYLAN S,TOPCU Y. Pyrolysis kinetics of hazelnut husk using thermogravimetric analysis[J]. Bioresource Technology,2014,156:182>-188. [26]DAMARTZIS T,VAMVUKA D,SFAKIOTAKIS S,et al. Thermal degradation studies and kinetic modeling of cardoon(Cynaracardunculus) pyrolysis using thermogravimetric analysis(TGA)[J]. Bioresource Technology,2011,102(10):6230>-6238. [27]CRIADO J M,MALEK J,ORTEGA A. Applicability of the master plots in kinetic analysis of non-isothermal data[J]. Thermochimica Acta,1989,147(2):377>-385. [28]YANG H,YAN R,CHEN H,et al. Characteristic of hemicellulose, cellulose and ligmin pyrolysis[J]. Fuel,2007,86(2):1781>-1788. [29]BURNHAM A K,ZHOU X,BROADBELT L J. Critical review of the global chemical kinetics of cellulose thermal decomposition[J]. Energy & Fuels,2015,29(5):2906>-2918. Kinetic Study of Tobacco Stem Waste Pyrolysis WU Wentao1, LI Zhihua1, ZHAO Beibei2 (1. China Tobacco Guangxi Industrial CO.,LTD, Nanning 530001, China; 2. Guangxi Tobacco Companies of CHINA TOBACCO, Nanning 530001, China) The pyrolysis kinetic of tobacco stem waste(TSW) was investigated by using single reaction model and three-parallel-reaction (TPR) model via thermogravimetric analysis(TGA). In single reaction model, the reaction mechanism of TSW pyrolysis presented as 14th order reactionf(α)=(1-α)14, with the apparent activation energy of 182.4 kJ/mol. According to the energy compensation effect results, the pyrolysis process of TSW could be divided into three stages which successively covered the conversion range ofα=0-0.32,α=0.32-0.80,α=0.80-1 with the pre-exponential factor of 2.88×1010, 4.33×1014and 9.76×1016, respectively. The single reaction model could not describe the pyrolytic mechanism of TSW reasonably. And then, the pyrolytic kinetic of TSW was investigated by using mixture Weibull distributed activation energy model(DAEM). Results showed that the mix-Weibull DAEM fitted the experimental data very well with correlation coefficients ofR2≥0.997 6. According to the results of mix-Weibull DAEM, the apparent activation energy of three pseudo components followed the order ofE0(lignin, 195.26 kJ/mol)>E0(cellulose, 152.54 kJ/mol)>E0(hemicelluloses, 121.18 kJ/mol). The pyrolytic mechanism for pseudo hemicelluloses was first-order reactionf(α)=1-α. And nucleation mechanism could be used to explain the pseudo cellulose pyrolysis. Order-based reaction mechanism was also suitable for pseudo lignin pyrolysis, however, the reaction order was between 3-4, which indicated that the pyrolytic mechanism of pseudo lignin was complex and might be a multiple steps reaction. tobacco stem waste;thermogravimetric analysis;pyrolysis kinetics;Weibull distribution TQ35 A 1673-5854(2017)05-0041-08 10.3969/j.issn.1673-5854.2017.05.007 2016- 08-10 务文涛(1985— ),男,河南开封人,硕士,研究方向为烟草化学工程、烟草配方研究 *通讯作者:赵贝贝(1987— ),女,硕士,研究方向为烟草化学、生物碱。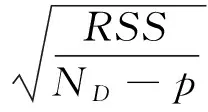

2 结果和讨论


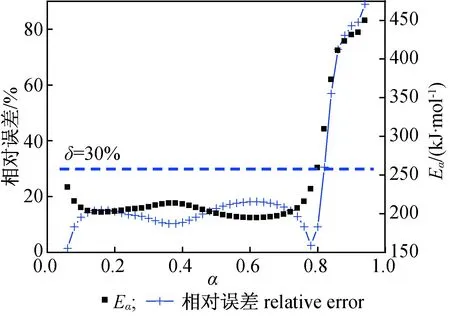
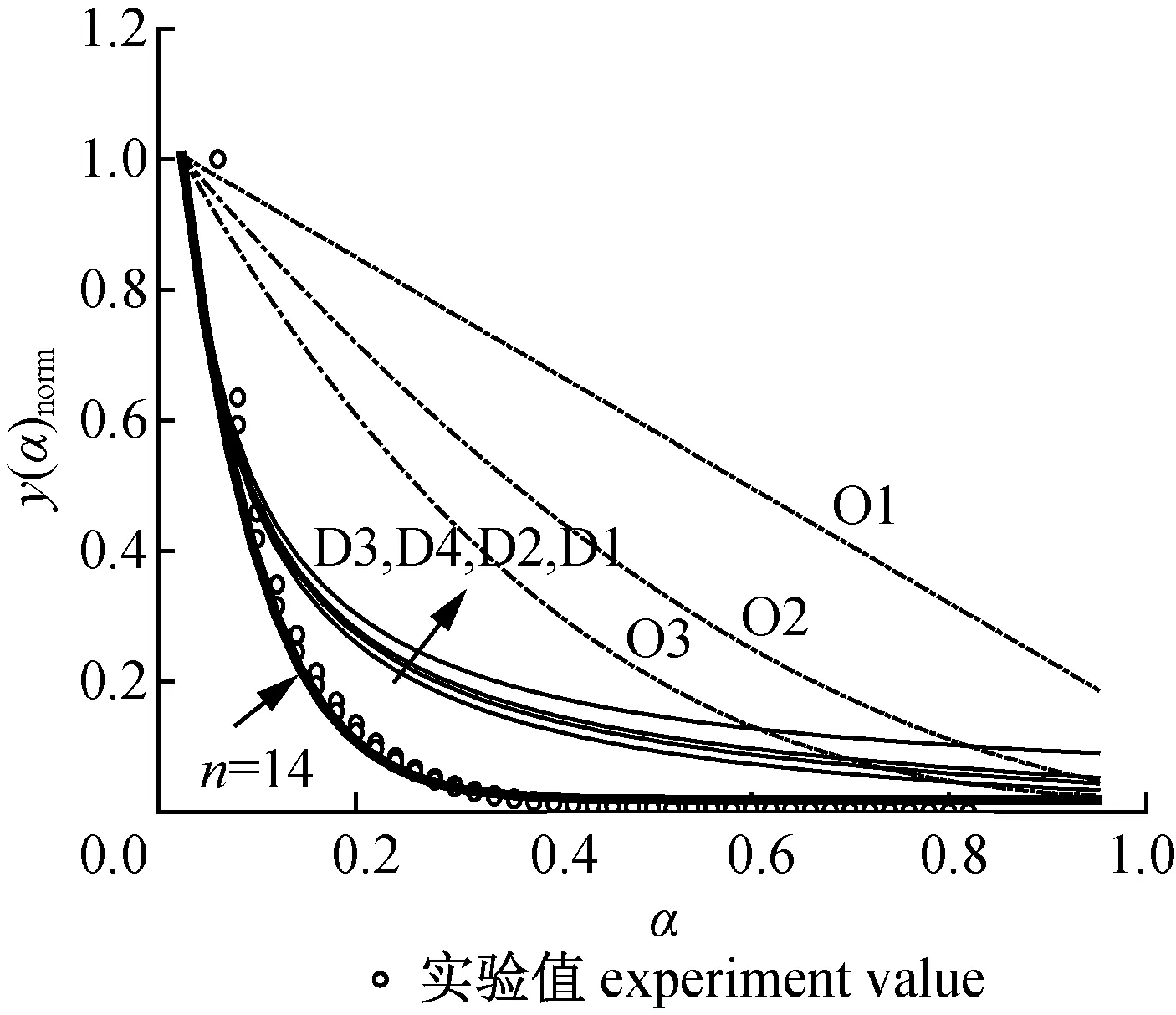




3 结 论
