青龙U型薄拱坝极限承载能力及渐进破坏模式分析

，， ，，

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072； 2.河南省水利勘测设计研究有限公司， 郑州 450016；3.水利部淮河水利委员会 安徽省水利科学研究院，合肥 230088)

青龙U型薄拱坝极限承载能力及渐进破坏模式分析

杨舒涵1，王均星1，杨凡2，查龙青3，漆天奇1

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072； 2.河南省水利勘测设计研究有限公司， 郑州 450016；3.水利部淮河水利委员会 安徽省水利科学研究院，合肥 230088)

U型碾压混凝土薄、高拱坝在国内外尚不多见，其中湖北省青龙拱坝因地形条件的独特尤为特殊，应力分布规律较常规V型拱坝有根本性差异，即在距坝底1/4坝高的下游坝面拱冠处出现较大面积的拉应力区，因此对青龙U型薄拱坝破坏机制及安全度的探讨非常必要。基于带拉破坏Drucker-Prager准则，利用强度储备系数法和超载法，分别对青龙拱坝的极限承载能力进行弹塑性有限元分析；运用位移突变法、塑性区贯通及收敛性等破坏判据，探讨其破坏机制，评价其整体安全度。结果表明:选用分析承载能力的方法不同，则青龙U型薄拱坝在极限承载过程中上、下游坝面破坏形态不同，但坝体最终的破坏形态基本一致;总结了其渐进破坏模式特点，并指出其在极限承载过程中由于应力的自行调整，拉应力减小或消失，满足稳定安全要求。

U形薄拱坝；极限承载能力；弹塑性有限元；渐进破坏模式；安全度

1 研究背景

碾压混凝土拱坝作为近几十年国内拱坝建设的主流，按照河谷形状的不同主要分为U型河谷拱坝和V型河谷拱坝。目前，国内外学者对常规V型拱坝的破坏机制做了大量的深入的研究[1-5]，认为 V型河谷高拱坝应力分布多以上游坝面承受拉应力，下游坝面承受压应力为主；坝体极限承载破坏规律依据拱坝的具体情况而各具特点；且坝体渐进破坏过程与失稳模式随模拟破坏的方法不同而改变。然而，U型碾压混凝土薄、高拱坝在国内外尚不多见，此类拱坝的应力及安全度研究亦很少。此外，目前基于非线性有限元的拱坝安全度评价中，很多学者只是将极限承载的最终计算结果作为主要依据，对拱坝在整个极限承载过程中的渐进破坏模式缺乏考虑，对破坏过程的分析层次不够明确[6]。

鉴于此，本文采用三维弹塑性有限元方法，分别利用强度储备法和超载法，对青龙U型薄拱坝进行渐进破坏过程计算分析。运用相应判据，对比分析拱坝在极限承载过程中的渐进破坏模式，研究其破坏机理，总结其破坏特点，并结合塑性破坏区的具体形态，确定青龙拱坝的整体安全性。

2 工程概况及计算模型

2.1 工程概况

青龙水电站位于湖北省恩施市的清江一级支流马尾沟。水电站主要挡水建筑物为抛物线形碾压混凝土双曲拱坝，坝址处地形条件较为特殊，河床宽35 m左右，坝顶处河谷宽109 m，岸坡坡角在628～737 m高程处高达60°～87°；两侧山体陡峻，呈狭窄的深U型。青龙拱坝厚高比为0.18，是极为典型的U型薄拱坝。拱坝坝顶高程为737.7 m，坝底高程为607.0 m，最大坝高为130.7 m，最大倒悬度为0.125。坝顶设置3个表孔用于堰顶溢流泄洪，堰顶高程727.0 m。大坝正常蓄水位为735.0 m，相应下游水位为613.0 m，淤沙高程为677.7 m。

2.2 弹塑性有限元计算模型

青龙拱坝三维有限元模型如图1所示，计算范围：坝基向上、下游分别延伸200 m和250 m，坝基向下延伸150 m，坝肩两侧依地形均沿高程向上延伸200 m。有限元计算网格采用8个节点六面体单元。计算模型单元总数为105 632个，节点总数为 117 081个。

图1 拱坝三维有限元网格模型Fig.1 Three-dimensional finite element models of the arch dam

岩体与混凝土材料采用Drucker-Prager本构模型。Drucker-Prager模型的屈服条件为

(1)

式中α，k为材料参数。计算采用的Drucker-Prager模型的屈服面是Mohr-Coulomb的外接圆锥，α，k与参数c，φ换算关系为：

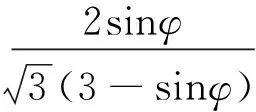
(2)

(3)

2.3 计算基本资料

根据青龙拱坝混凝土及岩石力学试验结果确定材料参数的取值。坝体混凝土重度为24 kN/m3，弹性模量E为22.0 GPa，线性膨胀系数Tl为9.0×10-6K-1，泊松比ν为0.167，摩擦系数f为1.4，黏聚力c为2.0 MPa；坝基重度为24 kN/m3，泊松比为0.33，各岩层弹性模量不同，自上而下分别为15.5，12.0，10.0，7.0 GPa。

温度荷载中，温降荷载是大坝产生裂缝的主要原因，且温降使拱轴线缩短，从而在坝踵引起附加拉应力，对大坝运行安全不利[7]。故本文选取正常运行期温降工况作为控制工况进行典型分析。计算荷载包括上游及下游坝面静水压力、结构自重、上游淤沙压力和运行期温降荷载[8](如表1所示)，运行期温降荷载的计算依据我国《混凝土拱坝设计规范》(SL 282—2003)，其公式为:

Tm=Tm1-Tm2-Tm0；

(4)

Td=Td1+Td2-Td0。

(5)

式中：Tm0，Td0分别为由封拱温度场决定的平均温度和等效温差；Tm1，Td1分别为由多年年平均温度场决定的平均温度和等效温差；Tm2，Td2分别为由多年年平均变化温度场决定的平均温度和等效温差；Tm，Td分别为截面平均温度和等效线性温差。

表1 青龙拱坝温度参数及温度荷载Table 1 Temperature parameters and temperature loads of Qinglong arch dam

注： 封拱温度场中各高程的Tm0=12 ℃，Td0=0 ℃

3 成果及分析

运行期温降工况下，青龙拱坝第一主应力、位移与塑性应变计算结果如图2所示。上游坝面主要为压应力，仅在左、右岸坝肩有呈线状分布的拉应力。下游坝面在距坝底1/4坝高的拱冠处出现了大面积的拉应力区，其值虽满足规范要求，但分布规律和常规V型拱坝有根本性差异。由于U型拱坝狭窄河谷的约束，上游坝面顺河向位移最大值出现在1/3坝高处，并以环形向四周辐射且逐渐减小。塑性破坏区按等效塑性应变>10-5作为破坏标准，坝体没有出现屈服区。

图2 D-P准则下坝体的应力、位移、塑性应变成果Fig.2 Stress,displacement and plastic strain under the D-P criterion

4 极限承载能力分析

拱坝极限承载能力计算方法通常采用强度储备法和超载法[9]。强度储备法即通过逐步降低材料强度，使正常工作状态的坝体达到结构破坏，材料强度储备系数(Kf，亦称降强系数)为材料设计强度与破坏强度的比值。超载法包括超水位法和超水重度法，即以抬高水位方式或增加水重度方式，直至坝体结构失去承载能力，超载系数(Kp)为破坏水压荷载与设计水压荷载比值，或破坏时水的重度与设计时水的重度之比值。

4.1 破坏判据

作为高次超静定结构，拱坝局部点的材料屈服破坏并不意味着结构承载能力的丧失。本文研究采用的破坏判据为：①位移突变法，表现为拱坝特征位置位移与超载系数关系曲线出现拐点；②塑性区贯通法，表现为屈服破坏区形成联通破坏机构；③收敛性判据，表现为塑性区发展太大引起迭代计算不收敛[10-11]。

图3 降强过程上、下游坝面典型等效塑性应变分布Fig.3 Typical equivalent plastic strain of dam body in the upstream and in the downstream in strength reduction process

4.2 强度储备能力分析

图4 拱冠梁处特征位置顺河向(y向)位移及其增幅与降强系数关系曲线Fig.4 Curves of displacement in y direction and displacement amplification vs.strength reduction coefficient at typical measuring points of arch crown beam

在正常运行期的温降工况下，采用降低原结构材料黏聚力c和内摩擦力φ值的方法，折减系数取0.2逐步进行青龙拱坝坝体渐进破坏过程的模拟，相应的渐进破坏、顺河向位移及增量演变过程如图3、图4所示。在降强过程中，各阶段破坏区的演变规律如下所述。

(1) 初始阶段：当Kf=1.7时，上游坝面右岸坝踵处开始出现小部位的塑性区，随着强度储备系数的增加，上游坝面两岸坝肩的塑性区呈线状由底部向顶部延伸；当Kf=2.0时，下游坝面坝趾处开始出现零星的破坏区，随着Kf的增大，破坏区不断扩大；在Kf=2.4时，塑性区沿下游坝面左、右岸坝肩及底部达到线状贯通；Kf=2.8时，上、下游建基面的塑性破坏区发展到2/3坝高及1/2坝厚的范围。

(2) 中间阶段：塑性区的发展主要表现为由坝底到坝顶、由坝面到坝内逐步扩展。坝体大面积屈服开裂以Kf=3.4为起点，此时，上、下游坝面溢洪道底部开始塑性屈服，坝底及左岸坝肩1/3坝高处塑性区由上游面至下游面贯通，此后，随着Kf的增大，上、下游坝面溢洪道底部的塑性区不断向四周蔓延；当Kf=4.0时，破坏区在上游坝面1/3～1/2坝高范围发生横向贯通，右岸建基面也形成上、下游面的贯通。

(3) 最终阶段：Kf=4.2时，下游坝面溢洪道底部出现横向贯通，形成联通的“θ”形塑性破坏区，建基面和上游坝面的绝大部分区域亦均处于塑性屈服状态，此时，坝体濒临破坏边缘；在Kf=4.4时，上、下游坝面完全破坏，坝体内部的上、下游贯通破坏区大范围出现，坝体与坝基接触部位“被掏空”，形成整体破坏贯通机构。从结构意义上讲，此时的拱坝高次超静定结构遭到破坏，其结构失稳，不具有承载能力。

(4) 从拱冠梁特征位置顺河向位移与降强系数关系曲线可以看出：在Kf<3.4时，顺河向位移随降强系数的改变基本呈线性变化，在Kf=3.4处拱冠梁剖面特征点顺河向位移演变曲线出现明显拐点，于Kf=4.4处逐渐趋于一致。从拱冠梁特征位置顺河向位移增幅与降强系数关系曲线中可以看出：当Kf<3.4时，特征点位移增量基本在0附近波动；之后，随着Kf的增大，增量逐渐增大。

此外，当Kf>4.4时,拉格朗日迭代计算不收敛。综上，强度储备系数Kf=4.4可作为D-P准则下青龙拱坝的溃坝特征点。

图5 超载过程上、下游坝面典型等效塑性应变分布Fig.5 Typical equivalent plastic strain of dam body in the upstream and in the downstream in loading process

4.3 超载能力分析

图6 拱冠梁处特征位置顺河向(y向)位移及其增幅与超载系数关系曲线Fig.6 Curves of displacement in y direction and displacement amplification vs.overload coefficient at typical measuring points of arch crown beam

本文采用超水重度系数法，基于正常运行期的温降工况，以0.2倍水重度逐步增加上游水压力进行拱坝坝体渐进破坏过程的模拟。拱坝在D-P准则下，超载渐进破坏、顺河向位移及其增量演化过程如图5、图6所示。在超载过程中，各阶段破坏区的演变规律如下所述。

(1) 超载初期：当Kp较小时，坝体材料处于弹性阶段，随着Kp的增大，上游坝面坝踵附近开始出现塑性破坏区，并沿建基面向坝顶缓慢发展；超载系数Kp=2.8时，上游坝面塑性区沿左、右岸坝肩及底部连通成线状；在Kp=3.4时，下游面中部坝趾处开始出现小部位破坏区域并不断向四周辐射扩展，左右岸建基面上游处的破坏区范围扩展到2/3坝高及1/2坝厚处。

(2) 超载中期：随着超载系数的增加，下游坝面塑性区由底部向顶部呈蔓延状扩展至1/3坝高处；此后，塑性区在坝面中部停滞发展，转而沿左右岸坝肩向坝顶蔓延。Kp=8.2时，上游坝面溢洪道底部开始出现破坏区，下游坝面左岸塑性区沿建基面发生由坝顶到坝底的竖向贯通；当Kp=8.6时，下游坝面破坏区沿右岸坝肩出现竖向贯通，之后，破坏区在下游面坝顶处由两岸向中部逐步扩展。

(3) 超载后期：Kp=11.4时，下游坝面沿顶部出现横向贯通，坝面四周的屈服破坏区相互联通形成“O”形破坏机构(表现为坝体未破坏区形成一个“空洞”并逐步向内部缩小)，上游坝面顶部出现横向贯通，随着Kp的增大，上游坝面顶部破坏区向底部迅速扩大；在Kp=11.8时，上游坝面全部塑性屈服，下游坝面仅在3/5坝高处存在孤立的未破坏区，建基面沿左右岸坝肩及底部屈服区形成上、下游贯通，坝体未破坏区可看成一个孤立的悬臂梁，于整个坝体而言，拱的支撑作用不复存在，坝体失稳。

(4) 从拱冠梁特征位置顺河向位移与超载系数关系曲线可以看出：Kp<8.6时，拱冠梁剖面特征点的顺河向位移随超载系数的增加呈线性变化；当Kp超过8.6后，特征点位移开始呈曲线变化；在Kp接近11.8时，特征点位移曲线随超载系数的增加逐渐趋于水平。从拱冠梁特征位置顺河向位移增幅与超载系数关系曲线可知：当Kp<8.6时,特征点位移增量大部分在8 mm附近波动；之后，随着Kp的增大，特征点位移增量逐渐变大，并在Kp接近11.8时大幅突增。

此外，当Kp>11.8时,拉格朗日迭代计算不收敛。综上所述，超载系数Kp=11.8可作为D-P准则下青龙拱坝的溃坝特征点。

为更清晰明了地展示青龙拱坝的渐进破坏形态，依据本文采用的破坏判据，拱坝极限承载过程中各主要特征强度储备系数和超载系数如表2所示。

表2 拱坝主要特征强度储备系数和超载系数Table 2 Values of overload coefficient and strength reserve coefficient of main failure stages of arch dam

4.4 渐进破坏模式特点分析

选用分析拱坝承载能力的方法不同，常规V型拱坝的渐进破坏过程和失稳模式各不相同。而青龙U型薄拱坝在渐进破坏过程中坝面破坏形态不同，但坝体最终的极限承载破坏形态基本相同。降强时，坝体上、下游坝面均表现为破坏区沿两岸建基面由坝底向坝顶扩展，形成“θ”形塑性贯通区；超载时，坝体下游坝面表现为塑性区由坝踵向坝顶呈片状蔓延至1/3坝高后停滞，继而沿两岸建基面向坝顶扩大，形成联通的“O”形贯通区。坝体最终的极限承载破坏形态均表现为坝体与坝基接触部位被“掏空”，拱结构变成悬臂曲梁形成失稳破坏。

在渐进破坏过程中，常规V型拱坝多表现为拱坝屈服区同时由顶部、底部向中部扩展的模式。而青龙U型薄拱坝表现为屈服区先由底部沿两岸坝肩向顶部扩展达到竖向贯通后，再在顶部达到横向贯通，继而向中部扩展形成坝体与坝基系统的整体贯通通道，最终失稳破坏。

5 结 论

基于三维弹塑性有限元方法，利用强度储备系数法和超水重度系数法对青龙拱坝进行极限承载能力及渐进破坏过程计算分析,得到如下结论。

(1) 青龙拱坝在D-P准则下的强度储备系数Kf=4.4，超水容重系数Kp=11.8。

(2) 青龙拱坝作为U型薄、高拱坝，由于狭窄河谷的约束，其应力分布规律不同于常规V型拱坝。距坝底1/4坝高的下游坝面拱冠处有较大面积的拉应力区，但在极限承载过程中由于坝体应力的自行调整，拉应力减小或消失，其稳定安全满足要求。

(3) 对于青龙U型薄拱坝而言，选用分析承载能力的方法不同，则对应的坝体渐进破坏过程中上、下游坝面破坏形态不同，但坝体最终的破坏形态基本相同。

(4) 青龙U型薄拱坝坝体的极限承载渐进破坏形态具有自身特点,主要表现为屈服区先由底部沿两岸坝肩向顶部扩展达到竖向贯通，继而在顶部形成横向贯通，再由四周向中部扩展，最终坝体与坝基系统形成整体贯通通道，导致失稳破坏。

[1] 董福品，朱伯芳，沈之良，等.国内外高拱坝应力分析概况[J].中国水利水电科学研究院学报，2003，1 (4):292-299.

[2] 周 伟，常晓林，唐忠敏，等.溪洛渡高拱坝渐进破坏过程仿真分析与稳定安全度研究[J].四川大学学报(工程科学版)，2002，34(4)：46-50.

[3] 甘海阔，赖国伟，李业盛.基于三维有限差分法的小湾拱坝施工步模拟及极限承载力分析[J].岩石力学与工程学报，2013，32(2)：3918-3927.

[4] 杨 剑，金 峰，王进廷，等.二滩拱坝极限承载力分析[J].清华大学学报(自然科学版)，2009，(9):56-59.

[5] 余天堂，任青文.锦屏高拱坝整体安全度评估[J].岩石力学与工程学报,2007,26(4):787-794.

[6] 任青文.高拱坝安全性研究现状及存在问题分析[J].水利学报， 2007,38 (9):1023-1029.

[7] 张国新，杨 波，张景华.RCC 拱坝的封拱温度与温度荷载研究[J].水利学报,2011,42(7):812-818.

[8] 查龙青，王均星，杨舒涵，等.青龙RCC拱坝封拱温度对拉应力的影响[J].水电能源科学，2016,34 (3):80-83.

[9] 王仁坤，张 冲，陈丽萍，等.特高拱坝结构安全度再评价[J].长江科学院院报,2014,31 (11):136-142.

[10] 王均星，张优秀，王汉辉.高拱坝承载能力研究[J].武汉大学学报(工学版),2004,37(1):27-31.

[11] 姜小兰，陈 进，孙绍文，等.高拱坝整体稳定问题的试验研究[J].长江科学院院报,2008,25 (5):88-93.

(编辑：姜小兰)

Ultimate Bearing Capacity and Progressive Destruction Mode ofQinglong U-shaped Thin Arch Dam

YANG Shu-han1,WANG Jun-xing1,YANG Fan2,ZHA Long-qing3,QI Tian-qi1

(1.State Key Laboratory of Water Resources and Hydropower Engineering Science,Wuhan University,Wuhan 430072,China; 2.Henan Water & Power Engineering Consulting Co.,Ltd.,Zhengzhou 450016,China; 3.Anhui & Huaihe River Institute of Hydraulic Research,Hefei 230088,China)

U-shaped thin and high arch dam is rarely seen all over the world.Qinglong arch dam in Hubei province is especially significant on account of its special terrain conditions.It is an RCC thin arch dam constructed in particular U-shaped river valley.The stress distribution of Qinglong arch dam is significantly different from that of conventional V-shaped dam.A large tensile stress area was found in the downstream arch crown which is 1/4 dam height from the bottom of dam.In view of this,discussions on the failure mechanism and safety of the dam are imperative.On the basis of the Drucker-Prager criterion,the ultimate bearing process of Qinglong arch dam is calculated and analyzed by using strength accumulation coefficient and overloading coefficient.Furthermore,by recording the abrupt change of dam displacement and observing the connected plastic zones and the convergence in the evolutionary process,the failure mechanisms of Qinglong arch dam is discussed and the safety degree is evaluated.Results suggest that different simulation methods lead to different destruction modes of dam in the upstream and downstream.But the final destruction patterns are consistent in general.As the stress of Qinglong arch dam in the ultimate bearing process adjusts itself,the tension stress decreases or disappears,and the safety of dam meets stability requirements.In addition,the characteristics of progressive failure mode of the dam are summarized.The research results offer important reference for similar projects.

U-shaped thin arch dam; ultimate bearing capacity; elasto-plastic finite element method; progressive failure mode; safety degree

TV642.43

A

1001-5485(2017)10-0139-06

2016-06-03；

2016-09-25

杨舒涵(1993-)，女，河南新乡人，硕士研究生，从事高坝结构设计理论与数值仿真研究，(电话)15237319668(电子信箱)Yang-SH@whu.edu.cn。

王均星(1963-)，男，湖北武汉人，教授，博士生导师，主要从事高坝设计理论(塑性极限分析)研究，(电话)13707182138(电子信箱)jxwang@whu.edu.cn。

10.11988/ckyyb.20160558 2017,34(10):139-144