组合弹性边界在基坑内支撑平面杆系有限元分析中的应用

， ，受祉，，，

(中南勘察设计院(湖北)有限责任公司，武汉 430071)

组合弹性边界在基坑内支撑平面杆系有限元分析中的应用

李松，马郧，李受祉，刘佑祥，张德乐，张晓玉

(中南勘察设计院(湖北)有限责任公司，武汉 430071)

内支撑平面杆系有限元计算是基坑支护结构设计不可或缺的一环，其中边界条件的选择尤为重要。为解决目前基坑内支撑平面杆系有限元计算中边界设置不合理的现状，引入仅受压法向弹簧与切向弹簧形成组合弹性边界，采用有限元方法对基坑内支撑平面计算进行分析，探讨了弹簧刚度系数对内支撑受力和变形的影响。研究结果表明：仅受压法向弹簧与切向弹簧很好地消除了传统约束对内支撑受力与变形的影响，不仅可得到准确的内支撑水平等效刚度，而且可精确计算各杆件内力；内支撑受力与仅受压法向弹簧和切向弹簧刚度系数无关；相比仅受压法向弹簧来说，切向弹簧对内支撑位移起控制作用。该组合弹性边界物理意义明确，弹簧刚度系数取值容易，可在基坑支护设计中推广应用。

组合弹性边界；基坑支护； 内支撑平面杆系; 仅受压法向弹簧；切向弹簧；有限元分析；等效刚度

1 研究背景

随着城市地下空间的快速开发和利用，基坑工程越来越多。规模大、深度深、周边环境复杂已成为基坑工程的显著特点。目前，基坑支护有多种形式，排桩或者地连墙加内支撑是目前应用较多的一种支护结构形式，内支撑因具有支撑刚度大，控制基坑变形和保护周边环境能力强，而且不侵入周围地下空间形成障碍物等优点而被广泛使用。但基坑内支撑计算中涉及2类问题:一类是弹性地基梁计算中内支撑简化为弹簧时弹簧刚度取值问题；另一类是弹性地基梁法中计算得到的内支撑反力作为围压荷载而进行内支撑平面杆系有限元计算的边界条件设置问题。针对简单的水平支撑，规范提供了水平刚度计算解析式[1-2]，同时也可使用杆系单元法计算，但对于复杂的内支撑，支撑刚度通常只能通过杆系单元法计算。这样一来，这2类问题其实可以划归为一类问题，即如何在内支撑平面杆系单元法计算中设置合理的边界条件。

国内学者[3-11]针对内支撑水平刚度的计算问题进行了深入的研究，取得了一定成果，但普适性较差，三维有限单元法由于建模复杂、耗时长等原因而不被广泛采用[12-14]；针对内支撑平面杆系有限元法计算中的边界设置问题，同济大学开发了内支撑和竖向桩墙共同分析的程序(BSC)，不作约束处理即可得到满意的结果，但这类程序目前尚未普及应用，且存在桩墙约束边界如何设置的问题。袁海庆等[15]针对围檩和内支撑与桩顶位移不协调的问题，提出了将排桩-内支撑-土压力空间体系转换为桩弹簧支座-内支撑-等效结点荷载“等价平面体系”，刘超等[16]提出了用位移约束代替铰约束的计算方法，并证明了该方法的可行性和实用性。

上述研究主要存在以下几个方面的问题。

(1) 桩墙对围檩的约束机理认识尚不全面。一般情况下，可认为围檩与桩墙之间为固结约束，桩墙对围檩的水平约束在任意方向均存在，可以将其分解为一个垂直于桩墙方向的约束和一个平行于桩墙方向的约束。

(2) 桩墙提供的水平刚度系数(即桩墙对围檩的约束刚度)计算问题。为方便描述，将垂直于排桩方向的约束称为法向约束，平行于排桩方向的约束称为切向约束。法向约束刚度系数可根据《建筑桩基技术规范》(JGJ 94—2008)[17]中关于基-桩协同工作和土的弹性抗力作用计算受水平荷载的桩基原理进行计算，该方法计算繁琐且存在一定的误差；而切向约束刚度系数目前研究较少，从实际情况看，切向约束刚度应远远强于法向约束刚度。

(3) 力与受力对象不匹配。如果考虑桩墙对围檩的法向约束，此时施加的围压荷载应该是作用在桩上的水平力，而不是作用在内支撑上的水平力；如果不考虑桩对围檩的法向约束，此时施加的围压应该是作用在内支撑上的水平力，而不是作用在桩上的水平力。目前基坑工程设计常采用弹性地基梁法，得到的内支撑反力已经考虑了桩墙水平约束作用，如果在内支撑平面计算中重新考虑桩墙的约束作用，势必会造成围压荷载被所设置的桩墙约束边界承担一部分，桩墙约束刚度越大，承担的围压荷载越大，计算结果误差也越大。

(4) 边界的设置问题是内支撑平面杆系有限元计算分析的重点和难点。直至目前，学者们提出了多种边界约束设置的方法，但或多或少存在一些问题，今后的研究重点应该是边界条件的设置。

(5) 对局部内支撑的计算目前较为普遍的做法是设置刚性约束，计算结果出现严重的应力集中现象。因此，使用弹性约束将成为研究趋势，尤其是对于局部内支撑变形和受力的计算。

因此，本文引入仅受压法向弹簧与切向弹簧形成组合弹性边界，以局部内支撑为例，采用有限元方法对基坑内支撑平面计算进行分析，探讨了弹簧刚度系数对内支撑受力和变形的影响，以期为内支撑平面杆系有限元分析的边界设置提供一种新思路和新方法。

2 组合弹性边界

对于复杂水平支撑体系，通常情况下作用在围檩上的围压荷载往往为不对称分布，为避免模型整体发生刚体位移，需设置必要的边界条件加以限制，目前采用较多的处理方法有以下3种[18]：

(1) 在模型的局部设置固定支座，这种方法一般在位移最小的位置设置固定支座来限制整体模型的刚体位移。

(2) 在模型的周边施加法向弹簧，这种方法在结构荷载法计算中经常用到，核心的问题是弹簧刚度系数的选取。

(3) 在模型的周边施加切向弹簧，从一般的基坑的实测变形情况来看，基坑周边的切向位移较法向位移要小得多，因此在周边加切线方向的约束弹簧会更加合理。

以上3种方法均需要一定工程经验来确定合理边界条件，选取固定支座位置和确定弹簧刚度系数人为性均较强，缺乏理论依据。

为此，本文将引入仅受压法向弹簧与切向弹簧形成组合弹性边界，以解决目前内支撑边界设置困难的现状。

2.1 仅受压弹簧

图1为弹簧工作原理。其中：L0为弹簧初始长度；L为弹簧变形后长度。

图1 弹簧工作原理Fig.1 Working principle of the spring

一般来说，弹簧应力-应变关系符合胡克定律，F=kx。其中：F为弹簧轴力(kN)；k为弹簧刚度系数(kN/m)；x为弹簧位移量(m)。下面引入一种特殊弹簧，即仅受压弹簧，其应力-应变关系符合以下规律：

F=k(L0-L)，L≤L0；

(1)

F=k(L-L0)且k=0，L>L0。

(2)

由式(1)和式(2)可以看出，仅受压弹簧即该弹簧在受压时符合胡克定律，在受拉时，弹簧将退出工作状态，此时的弹簧刚度系数为0，提供的反力也为0，但弹簧依旧可以变形。

图2 局部内支撑受力分析Fig.2 Force analysis for local inner support

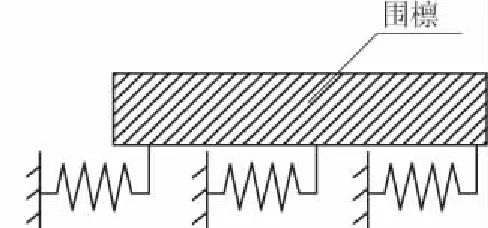
图3 切向弹簧示意图Fig.3 Tangential spring

2.2 切向弹簧

如图2所示，对于局部内支撑，围压合力的方向与仅受压法向弹簧提供的反力方向一致，仅受压法向弹簧还不足以平衡体系的外力，模型将发生整体漂移。因此，单纯使用仅受压法向弹簧作为局部内支撑的边界显然是不够的。

为此，引入平行于围檩方向的切向弹簧，如图3所示，切向弹簧为一般弹簧，既可受拉，也可受压，应力-应变关系符合胡克定律。切向弹簧可以平衡掉体系的外力，弥补仅受压弹簧的不足。

组合弹性边界受力特性见表1。

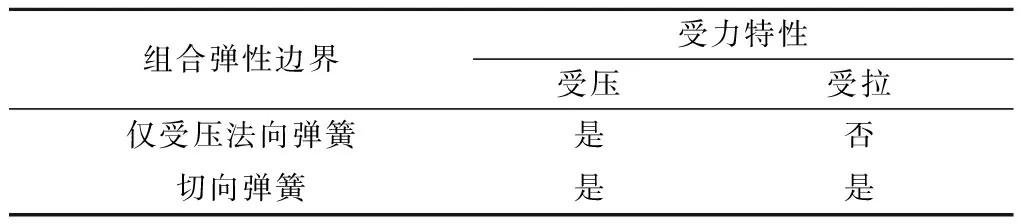
表1 组合弹性边界受力特性Table 1 Mechanical characteristics of the combined elastic boundary

2.3 组合弹性边界物理意义及参数取值

仅受压法向弹簧的物理意义：对于基坑工程，仅受压法向弹簧可视为周边地层对桩墙及内支撑的约束，土层受压不受拉(受拉可以忽略不计)，仅受压法向弹簧的工作机理与其一致。因此，仅受压法向弹簧是具有明确的物理意义的。

对于仅受压法向弹簧刚度系数的取值,建议从仅受压弹簧的物理意义出发，取土层的水平向基床系数作为仅受压弹簧的刚度系数，如表2[19]所示。

表2 水平向基床系数经验值Table 2 Empirical values of horizontal foundation modulus

切向弹簧的物理意义：在基坑工程中，桩墙对围檩的约束可分为法向约束和切向约束，通常切向约束刚度系数较法向约束刚度系数大许多。本文所阐述的切向弹簧即桩墙对围檩提供的切向约束，因此，切向弹簧同样是具有明确物理意义的。

对于切向弹簧刚度系数的取值可以从其实际物理意义的角度出发，取为桩墙所能提供的平行于围檩方向的水平刚度。切向弹簧边界的弹簧刚度系数Kt可按照地连墙与土体之间的摩擦阻力的刚度确定，如无资料，可以参考灌注桩桩侧阻力与位移的关系[20],即

(3)

式中：b为计算宽度(m)，对于连续墙可取1 m；h为计算高度(m)，可取地下室相邻两层层高的1/2；fs为土与围护结构间的侧摩阻力(kPa)，可参考灌注桩侧摩阻力取值；d为侧摩阻力达到最大值时的位移(mm)。

图4 弹性地基梁法计算模型Fig.4 Calculation model of elastic foundation beam method

3 内支撑平面杆系有限元分析

3.1 弹性地基梁法

弹性地基梁法将支护结构空间问题简化为平面应变问题考虑，主要适用于空间效应不明显的基坑支护结构。其中桩(墙)使用线弹性梁单元模拟，内支撑或者锚杆采用弹簧代替，基坑被动区采用土弹簧模拟，图4为弹性地基梁法计算模型，图中ea为主动土压力分布力。

3.2 支撑水平等效刚度

在采用弹性地基梁方法时需先确定弹性支座的刚度，对于较复杂的支撑体系难以直观地确定弹性支撑的刚度，且弹性支撑刚度会随着周边节点位置的变化而变化。一种较为简单的处理方式是在水平支撑的围檩上施加与围檩垂直的单位分布荷载p=1 kN/m，求得围檩上各节点的平均法向位移δ(与围檩方向相垂直的位移)，则弹性支座的水平刚度为

(4)

式(4)中求得的KBi反映的是水平支撑系统的一个平均支撑刚度。

3.3 内支撑受力分析

图5为桩(墙)与支撑受力分析。

图5 桩(墙)与支撑受力分析Fig.5 Stress analysis for pile(wall) and support

模型的简化需遵循力与受力对象相匹配的原则。当考虑桩墙的水平约束时，即弹簧提供拉压水平刚度，围压荷载F″应满足F″=F。

当不考虑桩墙的水平约束时，即弹簧不提供受拉方向的水平刚度，围压荷载F″应满足F″=F′。

实际工程中，通常采用弹性地基梁法计算所得到的是作用在内支撑上的力F′，此时就需要要求桩墙等效弹簧不提供受拉方向的水平刚度。如果弹簧提供受拉方向的水平刚度，造成的结果就是作用在内支撑上的力减小，其中一部分被弹簧分担，弹簧刚度越大，分担的围压荷载也就越大，最终造成较大的计算误差。

如果要使用F(作用在桩或者墙上的水平外力)与提供拉压水平刚度的弹簧组合计算也是可行的，但这样处理有2个难点，其一是F的计算，其二是弹簧水平刚度的计算，解决这2个难点非常困难，难以在实际工程中应用。

3.4 围压荷载

使用本文提出的组合弹性边界进行内支撑平面杆系有限元计算，其最终围压荷载p按照式(5)确定,即

p=p0+kΔ。

(5)

式中：p0为初始围压荷载，取自弹性地基梁法中桩单元计算得到的内支撑反力；Δ为围檩法向位移，Δ>0时，围檩朝向基坑内变形；Δ<0时，围檩朝向基坑外变形;k为仅受压弹簧刚度系数，Δ>0时，k=0；Δ<0时，k≠0。

图6 局部内支撑平面布置Fig.6 Plane layout of partial support structure

4 算例分析

图6为局部内支撑平面布置，对于该局部内支撑，采用仅受压弹簧和切向弹簧的组合弹簧边界进行计算分析。其中主梁尺寸为1 000 mm×800 mm，围檩尺寸为1 200 mm×800 mm，混凝土强度等级为C30，支撑水平间距均为8 m，支撑与围檩的水平夹角(锐角)为45°。仅受压弹簧水平刚度系数取为10 000 kN/m，切向弹簧刚度系数100 000 kN/m，初始围压荷载取为200 kN。图7与图8分别为水平位移云图和内力云图。

图7 水平位移云图Fig.7 Nephogram of horizontal displacements

图8 内力云图Fig.8 Nephogram of internal forces

根据静力平衡近似计算，EF杆件轴力近似解为2 262.7 kN， 而有限元计算结果为2 415.8 kN， 二者较为接近， 表明使用仅受压弹簧和切向弹簧所形成的组合弹簧作为模型边界， 可得到合理的计算结果。

4.1 切向弹簧刚度系数影响分析

为分析切向弹簧刚度系数的影响，取仅受压弹簧水平刚度系数为10 000 kN/m、切向弹簧刚度系数分别为40 000，100 000，1 000 000 kN/m3种情况进行对比分析，初始围压荷载取为200 kN。表3为水平位移，表4为内支撑内力。

表3 不同切向弹簧刚度系数下水平位移Table 3 Summary of horizontal displacements in the presence of varying stiffness coefficient of tangential spring

表4 不同切向弹簧刚度系数下内支撑内力Table 4 Summary of internal forces of inner support in the presence of varying stiffness coefficient of tangential spring

从表3可知，切向弹簧刚度系数对局部内支撑的位移有较大影响，随着切向弹簧刚度系数的增大，内支撑水平位移逐渐减小。大量基坑实测资料表明，基坑在角点处位移很小，当切向弹簧刚度系数分别为100 000 kN/m和1 000 000 kN/m时，局部内支撑角点B处的总水平位移分别为2.89 mm和0.34 mm，因此，切向弹簧的刚度系数建议取105～106kN/m。

从表4可知，切向弹簧刚度系数对局部内支撑的受力基本无影响，随着切向弹簧刚度系数的增大，内支撑轴力、剪力和弯矩基本没有变化，对围檩轴力有一定影响。切向弹簧虽然为拉压弹簧，但其合力方向平行于围檩，与围压荷载方向垂直，不会改变围压荷载，因而不会引起内支撑内力变化。

4.2 仅受压法向弹簧刚度系数影响分析

为探讨仅受压弹簧刚度系数的影响，取切向弹簧刚度系数为40 000 kN/m，仅受压弹簧刚度系数分别为1 000，10 000，100 000 kN/m进行对比分析。

从表5可知，随着仅受压法向弹簧刚度系数的增大，内支撑水平位移没有变化。由于切向弹簧对支撑体系的位移控制占主导地位，仅受压法向弹簧对内支撑位移的影响未能体现出来。因此，内支撑的位移主要受切向弹簧控制。同时从表6可知，在内支撑体系达到静力平衡状态后，仅受压法向弹簧刚度系数对局部内支撑的受力基本无影响。产生上述现象的原因在于仅受压法向弹簧的工作机理。对于初始围压荷载和内支撑布置形式相同的情况，内支撑体系的不平衡力是一定的。设置仅受压弹簧的目的是使得内支撑体系达到静力平衡状态，其产生的反力是一定的，只是由于弹簧刚度系数的不同，围檩所需要发生的朝向坑外的位移不同；而围檩朝向坑内位移的地方，由于仅受压弹簧受压不受拉，该地方的最终围压荷载还是原来的初始围压荷载，并没有由于仅受压弹簧而发生改变，围压荷载全部作用于内支撑体系，因而不会引起内支撑内力变化。

表5 不同仅受压法向弹簧刚度系数下水平位移汇总Table 5 Summary of horizontal displacements in the presence of varying stiffness coefficient of normal spring only subjected to compression

表6 不同仅受压法向弹簧刚度系数下内支撑内力汇总Table 6 Summary of internal forces of inner support in the presence of varying stiffness coefficient of normal spring only subjected to compression

4.3 组合弹性边界联合使用的必要性

(1) 对于局部内支撑，单独使用仅受压法向弹簧不能平衡内支撑体系的外力，会造成支撑体系漂移，无法得到合理的结果。

(2) 对于整体内支撑，支撑布置形状对计算结果影响较大，当整体内支撑较为对称时，单独使用仅受压法向弹簧基本可得到合理的计算结果，当整体内支撑形状极为不规则时，单独使用仅受压法向弹簧可能造成模型转动，同时忽略了桩墙平行于围檩方向的约束作用，是不合理的。

(3) 对于局部内支撑，即使在对称荷载作用下，当仅使用切向弹簧时，模型会有一定的转动趋势，如图9所示。

图9 仅使用切向弹簧时水平位移云图Fig.9 Nephogram of horizontal displacement in the presence of only tangential spring

因此，针对内支撑布置形式的差异性，仅使用仅受压法向弹簧或者切向弹簧均可能导致模型发生转动或者漂移，使计算结果不合理。而联合使用仅受压法向弹簧和切向弹簧所形成的组合弹性边界能避免这一问题发生，对于得到合理的计算结果是很有必要的。同时，仅受压法向弹簧和切向弹簧共同组成的组合弹性边界物理意义明确，弹簧刚度系数取值简单，适用于规则或者不规则的局部内支撑和整体内支撑。

5 工程应用实例

5.1 工程概况

武汉洪顶置业有限公司投资开发的长城汇项目位于武汉市中北路与姚家岭路交汇处，基坑开挖深度14.2～17.6 m，属深基坑，场地岩土工程条件较好，基坑东侧临近武汉地铁4号线，周边环境复杂，基坑采用的是钻孔灌注桩+2道钢筋混凝土支护方案。图10为内支撑平面布置，图中Q01—Q21为支护结构顶水平位移监测点。主撑截面为800 mm×650 mm，八字撑截面为700 mm×600 mm，连系梁为500 mm×550 mm。仅受压弹簧水平刚度系数取为10 000 kN/m，切向弹簧刚度系数取为40 000 kN/m，初始围压荷载根据弹性地基梁法计算得到的内支撑反力进行取值。

图10 内支撑平面布置Fig.10 Plan of inner support structure

5.2 计算值与实测值的对比分析

图11为变形前后水平位移云图，图12为支护结构顶水平位移对比。从图11可以看出，内支撑整体位移趋势合理，未发生刚体位移或者转动。从图12可知，支护结构顶水平位移计算值与实测值变化趋势基本一致，大部分监测点的水平位移数值吻合较好。

图11 水平位移云图Fig.11 Nephogram of horizontal displacement

图12 支护结构顶水平位移计算值与实测值对比Fig.12 Comparison of horizontal displacement on the top of support structure between calculation and measurement

6 结 论

本文引入仅受压法向弹簧与切向弹簧形成组合弹性边界，以局部内支撑为例，采用有限元方法对基坑内支撑平面计算进行分析，探讨了弹簧刚度系数对内支撑受力和变形的影响，并将组合弹性边界应用到实际工程案例中，与实测数据进行对比，得到了以下主要结论。

(1) 仅受压法向弹簧与切向弹簧很好地消除了传统约束对内支撑受力与变形的影响，不仅可得到准确的内支撑水平等效刚度，而且可精确计算各杆件内力。

(2) 内支撑受力与仅受压法向弹簧和切向弹簧刚度系数无关；相比仅受压法向弹簧，切向弹簧对内支撑位移起控制作用。

(3) 工程应用实例计算结果显示内支撑整体位移趋势合理，支护结构顶水平位移计算值与实测值变化趋势基本一致，大多数监测点的水平位移数值吻合较好，组合弹性边界具有较好的工程适用性和可靠性。

(4) 本文提出的组合弹性边界物理意义明确，弹簧刚度系数取值容易，可在基坑支护设计中推广应用。

[1] DB 42/T159—2012，基坑工程技术规程[S].武汉:湖北省建设工程标准定额管理总站,2012.

[2] JGJ 120—2012，建筑基坑支护技术规程[S].北京:中国建筑工业出版社，2012.

[3] 刘汉凯.基坑内支撑刚度计算方法辨析[J].佳木斯大学学报，2013，31(1):73-76.

[4] 葛 帆，王志人.基坑支护非对称荷载下支撑结构的刚度计算[J].城市勘测，2012，(4):73-76.

[5] 杨 敏，熊巨华.建筑基坑支撑结构体系水平刚度系数的计算[J].岩土工程技术，1999，(1):13-16.

[6] 陈林靖，戴自航.深基坑内撑式支护结构计算的综合刚度和双参数法[J].岩土力学，2010，31(3):891-895.

[7] 戴自航，苏美选，胡昌斌.抛物线分布荷载推力桩双参数法的2种数值解[J].岩石力学与工程学报，2007，26(7):1463-1469.

[8] 陈林靖，戴自航.基坑悬臂支护桩双参数弹性地基杆系有限元法[J].岩土力学，2007，28(2):416-419.

[9] 戴自航，沈蒲生.推力桩计算的综合刚度双参数法半数值解[J].福州大学学报，2004，32(6):741-746.

[10] 刘小丽，陈 芳，贾勇刚.深基坑内支撑等效刚度数值计算影响因素分析[J].中国海洋大学学报，2009，39(2):275-280.

[11] 陈 焘，张茜珍，周顺华，等.异形基坑支撑体系刚度及受力分析[J].地下空间与工程学报，2011，7(增1):36-39.

[12] 丁洪元，昌 钰，陈 斌.软土深基坑双排桩支护结构的影响因素分析[J].长江科学院院报，2015，32(5):105-109.

[13] 连宝琴，胡 斌，王新刚，等.武汉地铁名都车站基坑开挖监测与数值分析[J].长江科学院院报，2014，31(5):34-38.

[14] 梁志松.深基坑三维应力场和渗流场耦合分析与模拟[J].长江科学院院报，2014，31(5):79-83.

[15] 袁海庆，张光文.排桩-内支撑深基坑支护体系的等效转换与简化计算[J].岩土工程学报，2011，33(5):725-729.

[16] 刘 超，李受祉，张杰青，等.位移约束取代铰约束的内支撑平面单元计算方法[J].地下空间与工程学报，2013，9(增2):1886-1894.

[17] JGJ 94—2008，建筑桩基技术规范[S].北京:中国建筑工业出版社，2008.

[18] 王卫东，王建华.深基坑支护结构与主体结构相结合的设计、分析与实例[M].北京:中国建筑工业出版社，2007.

[19] 刘国彬，王卫东.基坑工程手册[M].北京：中国建筑工业出版社，2009.

[20] 王 涌，岳建勇.主体与支护结构结合的水平支撑系统数值分析[J].地下空间与工程学报，2005，1(4):591-594.

(编辑：陈 敏)

Application of Combined Elastic Boundary in Finite Element Analysisof Plane Bar Support System in Foundation Pit

LI Song,MA Yun,LI Shou-zhi,LIU You-xiang,ZHANG De-le,ZHANG Xiao-yu

(Central Southern Geotechnical Design Institute Co.,Ltd.,Wuhan 430071,China)

Finite element calculation of plane bar support system is an indispensable part of the design of foundation pit support,and the selection of boundary condition is especially important.To address the issue of unreasonable boundary setting in the finite element calculation of plane bar support system in foundation pit,a combined elastic boundary involving normal spring only subjected to compression and tangential spring is proposed in this article to investigate the influence of spring stiffness coefficient on the inner support force and deformation of foundation pit in finite element analysis.Results showed that by eliminating the influence of traditional constraints on the inner support force and deformation,the combined elastic boundary could result in a more accurate horizontal equivalent stiffness of inner support,and more precise internal forces.The inner support force has no concern with the stiffness coefficient of the normal spring only subjected to compression and the tangential spring.In addition,the displacement of inner support is controlled by the tangential spring rather than by the normal spring only subjected to compression.The proposed combined elastic boundary has clear physical meaning,and the value of spring stiffness coefficient is easy to obtain,hence could be applied to the design of foundation pit support.

combined elastic boundary；foundation pit support; plane bar system of inner support; normal spring only subjected to compression；tangential spring；finite element analysis；equivalent stiffness

TU473

A

1001-5485(2017)10-0095-07

2016-05-31；

2016-07-21

武汉市“黄鹤英才(专项)计划”资助项目(武人才[2014]10)；武汉市城建设委员会科研项目(201545，武城建[2015]191)

李 松(1986-)，男，湖北嘉鱼人，工程师，硕士，主要从事深基坑工程设计与研究工作，(电话)18696130167(电子信箱)731975786@qq.com。

马 郧(1970-)，男，湖北天门人，教授级高级工程师，博士，主要从事岩土工程勘察、深基坑工程设计与研究工作，(电话)13971668934(电子信箱)282437271@qq.com。

10.11988/ckyyb.20160539 2017,34(10):95-101