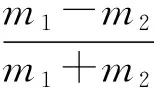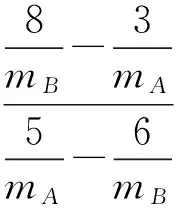恢复系数在一维碰撞中的巧妙运用
2017-10-24陈长
陈 长
(惠州一中实验学校,广东 惠州516000)
恢复系数在一维碰撞中的巧妙运用
陈 长
(惠州一中实验学校,广东 惠州516000)
2017年高考改革,原本选修3-5纳入必考范围.与动量相关的知识点必将成为高考热点问题,其中一维碰撞问题是动量守恒类问题的重中之重.本文主要探讨一维碰撞问题下的速度变化,将恢复系数引入到碰撞问题的简单计算中.
恢复系数; 一维碰撞; 速度
一般的参考书上重点讨论一维碰撞中的弹性碰撞和完全非弹性碰撞.高考对碰撞类的考查侧重于对动量守恒规律的运用,往往涉及繁琐的计算.若在该类问题中巧妙运用恢复系数将有利于迅速解题.
质量分别为m1和m2的物块分别以初速度v1和v2在光滑的水平地面上发生碰撞,碰撞之后,m1和m2的速度分别为v1′和v2′.规定m1的初速度v1为正方向,那么m1和m2的接近速度v12>0(接近速度v12=v1-v2),m1和m2的远离速度v21′≥0(远离速度v21′=v2′-v1′).
引入恢复系数为

(1)
两物块发生碰撞满足动量守恒,有
m1v1+m2v2=m1v1′+m2v2′.
(2)
碰撞之后动能不能增加,故有
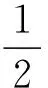
(3)
结合实际情况v21′≥0,以及(3)式可以得到
0≤e≤1.
由(1)式和(2)式可得

(4)

(5)
两物体的初速度亦可以表示成如下形式

(6)

(7)
在(4)~(7)式中,等式右边的第1项为质心的速度,第2项为质点相对于质心的速度.可以发现碰撞后质点相对质心的速度对于碰撞前质点相对与质心的速度多出系数-e.碰撞前后质心的速度没有发生改变,质点系的质心做匀速直线运动.碰撞前后速度的改变本身只发生在质点相对于质心的速度上.
在(4)式和(5)式中,恢复系数在0≤e≤1的范围内.当碰撞为弹性碰撞时,e=1.当碰撞为完全非弹性碰撞时,e=0.而碰撞为非完全弹性碰撞时,0 (8) (9) 例1.(2009年全国卷Ⅰ第21题)质量为M的物块以速度v运动,与质量为m的静止物块发生正碰,碰撞后两者的动量正好相等,两者质量之比M/m可能为 (A) 2. (B) 3. (C) 4. (D) 5. 例2.动量分别为5 kg·m/s和6 kg·m/s的小球A、B沿光滑平面上的同一条直线同向运动,A追上B并发生碰撞后.若已知碰撞后A的动量减小了2 kg·m/s,而方向不变,则A、B质量之比可能是 (A) 5∶6. (B) 3∶8. (C) 1∶2. (D) 4∶7. 常规解法: 碰撞过程中系统动能不增加;碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理. 1 张大同,黄洪才,彭大斌.物理竞赛教程(高一年级)[M].第5版.上海:华东师范大学出版社,2016:167-169. 2 [俄]朗道,栗弗席兹.朗道理论物理教程(卷01)-力学(第5版)[M].李俊峰,鞠国兴,译.北京:高等教育出版社,2007:45-46. 2017-04-12)