轴向移动绳固有频率计算和分析
2017-10-24陈恩伟陆益民刘正士
仲 凯, 陈恩伟, 罗 全, 陆益民, 刘正士
(合肥工业大学 机械工程学院,安徽 合肥 230009)
轴向移动绳固有频率计算和分析
仲 凯, 陈恩伟, 罗 全, 陆益民, 刘正士
(合肥工业大学 机械工程学院,安徽 合肥 230009)
文章以轴向移动绳为研究对象,分析了定长度和变长度2种移动绳系固有频率和受迫振动特性。利用传播波在绳中反射的振动周期和固有振型规律,研究了轴向移动绳振动特性;通过Matlab数值仿真,对比了定长度和变长度2种移动绳固有频率的差异以及绳系的轴向移动速度和张紧力变化对其固有频率的影响;并利用四阶Runge-Kutta法,计算了轴向移动绳受迫振动的横向位移响应。
轴向移动绳;变长度;固有频率;受迫振动;传播波
0 引 言
传送带、带锯、磁带、升降电梯以及绳系卫星等工程设备物理模型可以简化为轴向移动绳系。这些工程设备的振动问题严重地影响其在实际工程中的使用效果和安全性。如带锯的振动影响加工产品的质量;磁带的振动影响其音质和使用寿命;升降电梯的振动影响电梯的稳定性、舒适性和安全性,严重时甚至会产生安全事故等。因此,对轴向移动绳系振动问题的研究十分必要。文献[1]利用相位封闭原理研究了轴向移动绳的频率变化和能量损失问题;文献[2]通过实验得出移动绳两端无约束情况下的固有振型,并与理论计算之间进行了对比;文献[3]利用拉格朗日方程和有限元法建立了轴向移动绳模型,研究了轴向移动绳的自由振动响应和能量变化问题;文献[4]通过Hamilton原理研究了变长度的横向位移响应和能量问题;文献[5-6]研究了附加子系统的轴向移动绳系固有频率以及引起系统共振的因素;文献[7]研究了轴向移动绳在两端自由移动情况下的振动特性,发现当绳系两端靠近时系统会发生高频振动问题;文献[8]研究了高速电梯运动,发现在电梯上行阶段系统的振动幅值和频率有增大的现象;文献[9]研究了电梯悬挂系统在外界激励下的横向位移响应和固有频率变化问题,分析了频率变化规律。
本文主要运用绳系中传播波特性来计算绳系的固有频率,分析绳系固有频率的影响因素和外界激励下的受迫振动响应。
1 轴向移动绳模型
轴向移动绳模型如图1所示,建模基于以下假设:轴向移动绳线密度、张紧力在运动过程中保持不变;忽略轴向移动绳纵向振动的影响,且轴向移动绳的横向振动引起的弹性变形远小于轴向移动绳长度。轴向移动绳中张紧力为常量P,绳的线密度为ρ,外界激励力为f(x,t),横向位移为w(x,t),则系统方程[1]为:
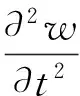
(1)
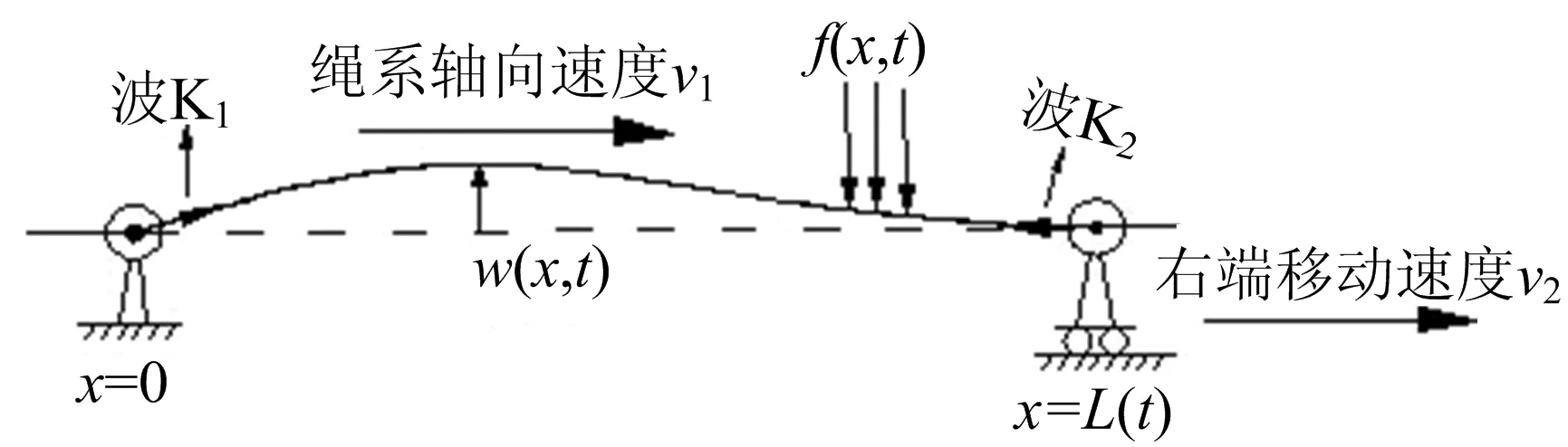
图1 变长度轴向移动绳模型

2 轴向移动绳中的传播波
利用驻波特性来分析轴向移动绳问题,即将绳中驻波分解为2个反方向的传播波[10]来表示:
w(x,t)=Aei(ω t-kx)=A1ei(ω t-k1x)+A2ei(ω t-k2x)
(2)
其中,A1、k1为波K1的幅值和波数;A2、k2为波K2的幅值和波数。波在绳中遇到不同边界条件反射时,波长与绳长之间的关系满足不同规律。当边界条件满足w(0,t)=w(L,t)=0时,即横向位移为0,则有:
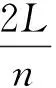
(3)
假设波K1从绳子左端移动到右端的时间为t1,返回左端的时间为t2,由(3)式波长与绳长的关系可得轴向移动绳n阶固有振型对应的振动周期为:
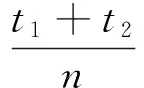
(4)
3 固有频率和受迫振动响应
3.1 定长度绳
图1中,当v1=0,v2=0时,移动绳模型简化为两端固定且不可轴向移动,此时绳长为初始长度L0。波K1从绳子左端移动到右端的往返时间分别为t1=L0/u,t2=L0/u,则有:
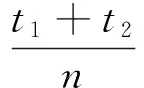
其中,u为波速。固有频率为:

(5)
当v1≠0,v2=0时,移动绳模型简化为两端固定但能在支撑环中轴向移动且速度为v1,此时绳长为初始长度L0。波K1从绳子左端移动到右端的往返时间分别为t1=L0/(u+v1),t2=L0/(u-v1),则有:
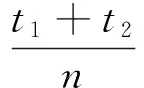
固有频率为:
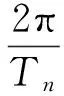
(6)
当(6)式中的轴向移动速度v1=0时,(6)式转化为(5)式,即绳系无轴向移动。选取轴向移动绳参数如下:L0=18 m,ρ=0.010 kg/m,v2=0。通过(5)式和(6)式计算发现,有轴向移动速度时,定长绳的固有频率ωn随轴向速度v1的增大而减小;固有频率ωn随张紧力P的增大而增大,变化规律如图2所示。
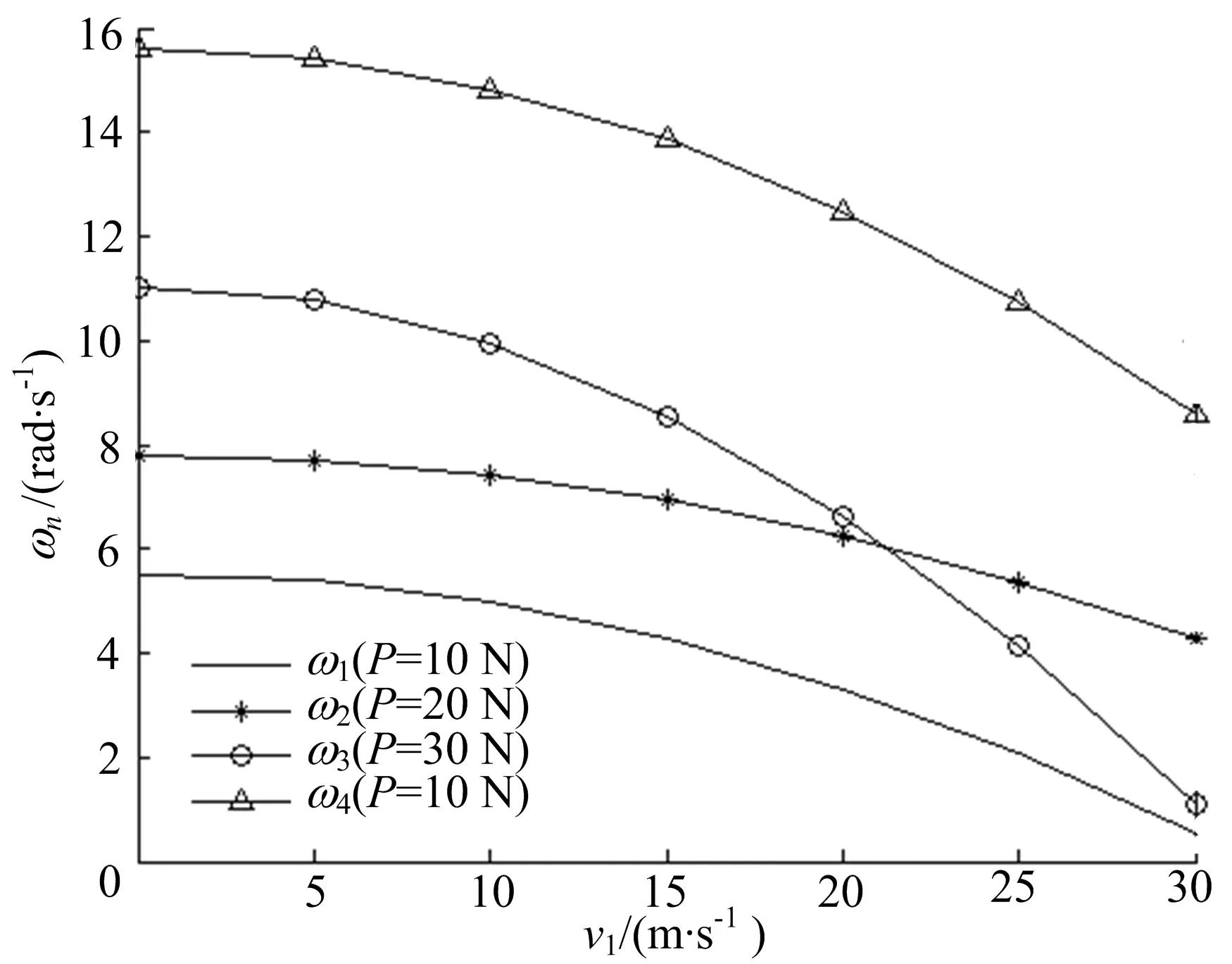
图2 轴向移动绳固有频率的变化规律
施加外界激励力F=sin(πt) N,分别作用在绳x=(1/4)L,x=(1/2)L,x=(3/4)L处。移动绳参数选取同上,此时张紧力P=20 N。利用四阶Runge-Kutta法,计算轴向移动绳系中点处的横向位移响应,结果如图3所示。
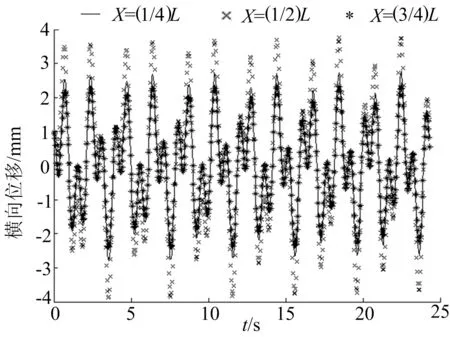
图3 外界激励下轴向移动绳中点处横向位移响应
当外界激励力F=sin(ωt) N时,激励频率分别取ωa=7.0 rad/s和ωb=7.8 rad/s时,轴向绳系中点处横向位移分别如图4a和图4b所示,产生了拍振和共振现象。当外界激励力频率接近或者等于系统一阶固有频率ω1=7.8 rad/s(见图2,P=20 N,v1=0)时,中点处振幅明显增大,产生强烈的振动现象。

图4 拍和共振现象
3.2 变长度绳
图1中,当v1=0,v2≠0时,轴向移动绳模型简化为右端可轴向移动但绳系左端固定且不能在支撑环中移动,移动绳长度L(t)=L0±v2t,且绳系左右两端各有波K1和波K2相向运动。假设波K1第1次到达绳子右端时间为t1和此时波K2经过时间t1后位置为x1。当K1运动到绳子右端点有(u+v2)t1=L0+v2t1,移动到右端时间为:
t1=L0/u
(7)
此时绳子长度为:
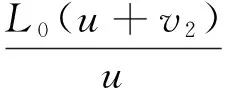
(8)
波K2的位置为:
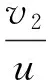
(9)
波K1第1次到达绳子左端的时间t2(从波K1第1次到达绳子右端开始计时)为:
(10)
此时绳长为:
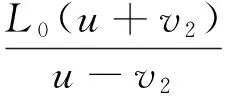
(11)
波K2第1次到达绳子左端点时间为:
(12)
显然t1′小于t2,因此波K2先到达左端点,并且此时波K2的位置x2恰好在绳子右端点,即
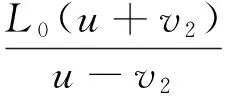
(13)
则第1个运动周期为:
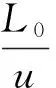
(14)
波K1第2次从绳子左端到达绳子右端再返回,与第1次运动过程相同,则运动周期为:
(15)
以此类推第m个运动周期为:
(16)
故
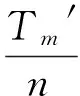
(17)
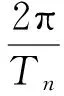
(18)
当(18)式中右端移动速度v2=0时转化为(5)式,此时变长度轴向移动绳为定长度绳。变长度移动绳参数选取如下:L0=18 m,ρ=0.010 kg/m,P=20 N,v1=0。由(18)式计算发现,变长度绳的固有频率随着绳子伸长(v2>0)而减小,随着绳子缩短(v2<0)而增大;且轴向移动速度越大,频率变化越快。绳系伸长和缩短时固有频率的变化如图5所示。
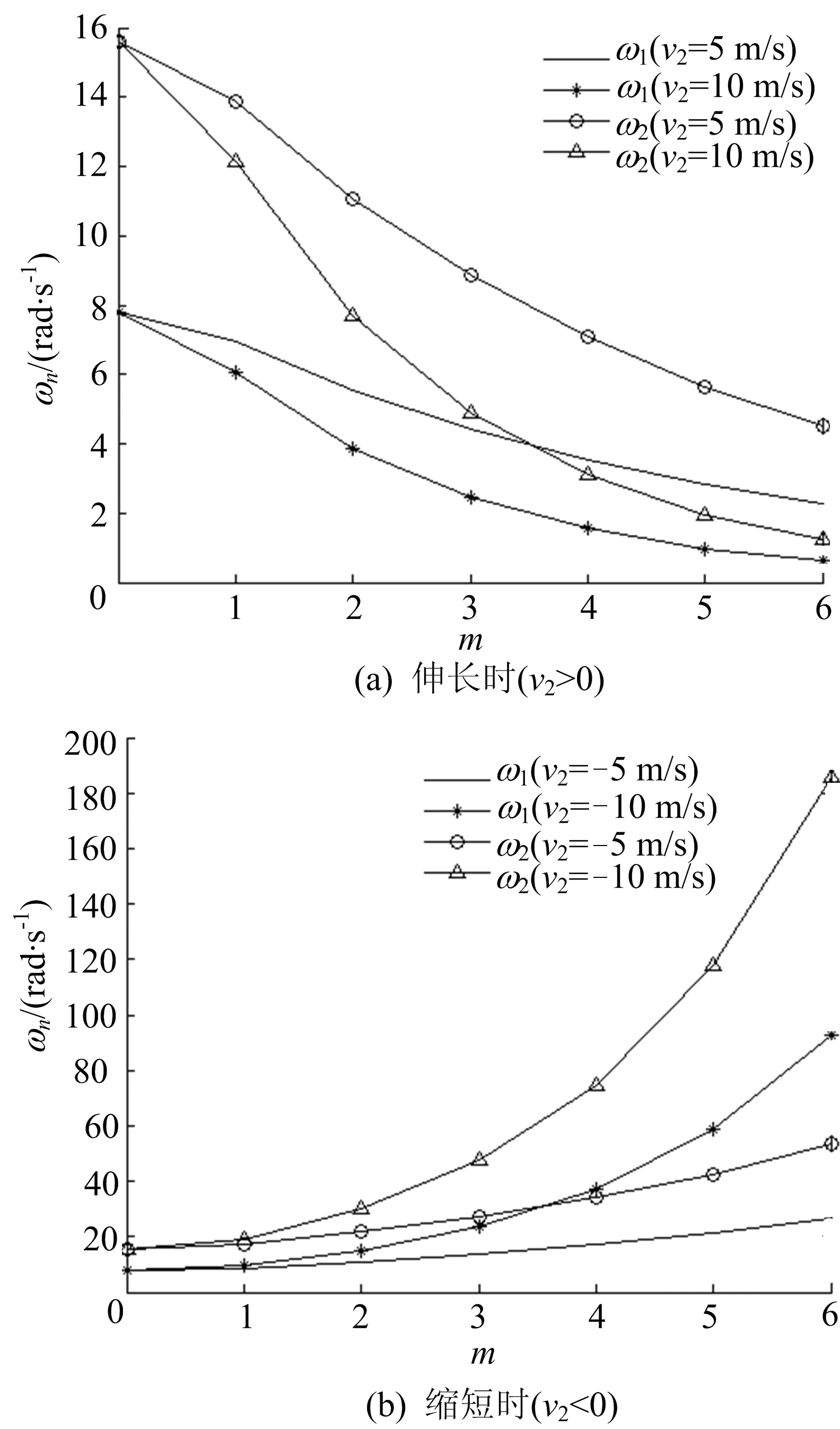
图5 绳系伸长和缩短时固有频率的变化规律
4 结 论
(1) 本文利用传播波固有振型和振动周期之间的关系分析了轴向移动绳系(定长度和变长度)的固有频率。变长度轴向移动绳的固有频率随着绳长伸长(v2>0)固有频率减小,随着绳长缩短(v2<0)固有频率增大;且轴向移动速度v2越大,频率变化越快。
(2) 分析了轴向移动速度v1对定长度轴向移动绳固有频率的影响。定长度轴向移动绳固有频率与轴向移动速度v1呈负相关,且轴向移动速度v1的变化越大,固有频率变化越快。
(3) 分析了张紧力P对轴向移动绳(定长度和变长度)固有频率的影响。轴向移动绳固有频率与轴向移动绳张紧力呈正相关,张紧力越大,固有频率越大。
[1] LEE S Y,LEE M.A new wave technique for free vibration of a string with-varying length[J].Journal of Applied Mechanics,2002,69(1):83-87.
[2] KASHY E,JOHNSON D A,MCINTYRE J,et al.Transverse standing waves in a string with free ends[J].American Journal of Physics,1997,65(4):310-313.
[3] CHEN E W,FERGUSON N S.Analysis of energy dissipation in an elastic moving string with a viscous damper at one end [J].Journal of Sound and Vibration,2014,333(9):2556-2570.
[4] SANDILO S H,HORSSEN W T V.On variable length induced vibrations of a vertical string[J].Journal of Sound and Vibration,2014,333(11):2432-2449.
[5] FUNG R F,HUANG J S,CHU J J.Dynamic stability of an axially travelling string/slider coupling system with moving boundary [J].Journal of Sound and Vibration,1998,211(4):689-701.
[6] CHEN J S.Natural frequencies and stability of an axially-traveling string in contact with a stationary load system[J].Journal of Vibration and Acoustics,1997,119(2):152-157.
[7] RAM Y M,CALDWELL J C.Free vibration of a string with moving boundary conditions by the method of distorted images [J].Journal of Sound and Vibration,1996,194(1):35-47.
[8] 张鹏,朱昌明,张梁娟.变长度柔性提升系统纵向-横向受迫耦合振动分析[J].工程力学,2008,25(12):202-207.
[9] 王文,钱江.电梯悬挂系统在建筑摇晃引起位移激励下横向振动分析[J].振动与冲击,2013,32(7):70-73.
[10] SINGIRESU S R.Mechanical vibrations[M].4th ed.Singapore:Pearson Prentice Hall,2004.
Calculationandanalysisofnaturalfrequencyforanaxiallymovingstring
ZHONG Kai, CHEN Enwei, LUO Quan, LU Yimin, LIU Zhengshi
(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)
Aiming at an axially moving string with constant and variable length, the problems of natural frequency and forced vibration are investigated. Dynamic characteristics of axially moving string are studied by vibration period and natural mode of transverse wave on the string. The difference in natural frequency between axially moving string with constant length and that with variable length is obtained by numerical simulations using Matlab. The relationship between the natural frequency and the axial speed and tension is obtained. Transverse displacement response of forced vibration is obtained by numerical simulations using fourth-order Runge-Kutta method.
axially moving string; variable length; natural frequency; forced vibration; transverse wave
2016-01-04;
2016-03-10
国家自然科学基金资助项目(51305115;51675150)
仲 凯 (1990-),男,江苏泗阳人,合肥工业大学硕士生;
陈恩伟 (1979-),男,广西合浦人,博士,合肥工业大学副教授,硕士生导师,通讯作者,E-mail:cew723@163.com.
10.3969/j.issn.1003-5060.2017.09.003
TB123
A
1003-5060(2017)09-1164-04
(责任编辑 胡亚敏)
