基于双迭代学习-交叉耦合的双轴误差控制

许 万, 郑 威, 杨 维, 曹 松, 罗 西

(湖北工业大学 机械工程学院,湖北 武汉 430068)

基于双迭代学习-交叉耦合的双轴误差控制

许 万, 郑 威, 杨 维, 曹 松, 罗 西

(湖北工业大学 机械工程学院,湖北 武汉 430068)

在双轴高精度轮廓加工中,单轴的跟踪误差和双轴间运动不协调产生的轮廓误差都会影响加工精度。文章提出了一种基于双迭代学习-交叉耦合的双轴运动控制策略,将单轴的迭代学习控制(iterative learning control,ILC)与双轴的交叉耦合控制(cross-coupled control,CCC)以及轮廓误差的ILC相结合。单轴的ILC用来改善单轴的跟踪性能,减小单轴的跟踪误差;双轴的CCC用以增加各轴之间的匹配程度,减小轮廓误差;轮廓误差的ILC可以提高轮廓的跟踪性能,进一步削减轮廓误差。仿真结果表明,双迭代学习-交叉耦合控制系统不仅能够有效降低单轴的跟踪误差,而且能显著减小轮廓误差。

交叉耦合;迭代学习;轮廓误差;跟踪误差;双迭代学习-交叉耦合

对于多轴运动系统,各轴之间运动不协调而产生的轮廓误差是影响复杂型面零件加工精度的主要因素,各单个轴在加工过程中产生的跟踪误差也是影响零件加工的重要因素。因此,在有效减小轮廓误差的同时降低单个轴的跟踪误差,对于提高零部件加工精度是极其重要的。

近年来,许多学者都对提高加工精度的控制方法进行了研究。通过迭代学习控制(iterative learning control,ILC)[1]、滑模控制[2]、自适应控制[3]以及零相位误差跟踪控制[4]等方法能够有效减小单轴的跟踪误差,但是不能从根本上减小系统的轮廓误差。为削减多轴运动不匹配引起的轮廓误差,文献[5]提出了交叉耦合控制(cross-coupled control,CCC);文献[6]提出了变增益交叉耦合控制。一些学者将现代控制技术与交叉耦合控制方法相结合,以更好地减小轮廓误差。文献[7]提出了一种基于轮廓误差传递函数(contouring error transfer function,CETF)的单变量CCC方法,可以得到满足交叉耦合增益变化的具有稳定性和鲁棒性的CCC补偿器;文献[8]在CETF基础上采用极点配置法设计了一个PI型CCC控制器;文献[9]提出了一种基于任务坐标系(task coordinate frame,TCF)的多变量CCC方法;文献[10]提出了基于零相位误差跟踪控制器的轮廓误差交叉耦合控制;文献[11]提出了一种基于多层模糊控制的交叉耦合补偿方法;文献[12]提出了基于遗传算法的变增益交叉耦合控制;文献[13]提出了直线电机XY平台交叉耦合迭代学习控制。文献 [5-13]等方法能够较好地减小运动系统的轮廓误差,但是不能有效地降低单轴的跟踪误差,提高单轴的跟踪性能。

针对目前加工制造业多为零部件的重复性加工运动,本文设计了将单轴的迭代学习控制和双轴的交叉耦合-迭代学习控制相结合的控制方法。在Matlab/Simulink下搭建仿真模型,仿真结果表明,利用该方法不仅能够大幅降低单轴的跟踪误差,而且更能有效减小轮廓误差,提高轮廓加工精度。

1 永磁同步电机数学模型

在数控加工、机器人控制和高精度加工等领域,永磁同步电机都有着及其重要的应用。因为永磁同步电机数学模型是一个非线性、强耦合的多变量系统,所以不能完全适应高动态性能的调速系统或者伺服系统。因此,建立永磁同步电机的数学模型并将其简化是研究运动控制的首要问题[14]。

将建立在三相静止坐标系上的永磁同步电机的数学模型通过坐标变换转换到互相垂直的两相坐标系上,这样使得两相绕组之间没有磁的耦合,从而简化永磁同步电动机的模型。经过矢量转换的永磁同步电机模型等效于直流电动机的模型,因而可以获得与直流电动机相类似的特性[14]。采用矢量变换的永磁同步电机数学模型可以简化为:

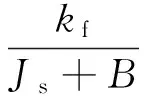
(1)

其中,kf为常值比例系数;Js为电机动子的质量;B为黏滞摩擦系数。

2 双迭代学习-交叉耦合控制

2.1 交叉耦合控制CCC

CCC系统的主要目的是消除多轴运动系统的轮廓误差,而不是减小单个轴的跟踪误差[6]。CCC系统框图如图1所示。其基本控制思想是:多轴运动系统的轮廓误差由各单轴的跟踪误差经过实时轮廓误差估计模型计算得到,经过交叉耦合控制器的作用产生一个新的控制信号,再经过轮廓误差分配模型补偿到各轴以消除每个轴对其他轴的影响,从而达到减小运动系统轮廓误差的目的。本文采用比例误差分配方法进行误差补偿,这是由于该方法不仅可以控制不同轴的分配量,而且不会为了得到合适的分配参数而不断修改权值增加计算量,同时也不会因为各轴之间误差较大而造成补偿失调[15]。

图1 CCC系统框图

图1中,轮廓误差ε的计算与交叉耦合增益系数Cx、Cy密切相关。因此,要计算运动系统的轮廓误差ε,就必须先计算出交叉耦合增益系数Cx、Cy以及单轴的跟踪误差Ex、Ey。

根据文献[6]的轮廓误差建模方法可知,轮廓误差的计算公式为:

ε=EyCy-ExCx

(2)

其中,Ex=xr-xs,Ey=yr-ys,xr、yr分别为x、y轴的期望轨迹,xs和ys分别为x、y轴的实际轨迹。

对于期望直线轮廓运动轨迹,可将其交叉耦合增益系数定义为:

Cx=sinθ,Cy=cosθ

(3)

对于期望圆形轮廓运动轨迹,其交叉耦合增益系数可定义为:

(4)

对于期望一般曲线轮廓运动轨迹,其交叉耦合增益系数可定义为:

(5)

其中,θ为某一时刻期望轨迹或者其切线方向与x轴的夹角;R为期望圆形轮廓运动轨迹的半径;ρ为该时刻期望一般曲线轮廓运动轨迹的曲率半径。

2.2 迭代学习控制ILC

ILC适用于具有某种重复运动特性的被控对象,可以实现有限时间区间上的完全跟踪任务[16]。迭代学习的控制思想是:对于具有重复运动的控制系统,每次控制都将前一次期望轨迹和实际轨迹的误差信号作为修正控制输入信号,以此产生一个新的控制信号,使得该重复运动系统在下一次执行中有更好的轮廓跟踪效果。ILC的系统框图如图2所示。

图2 ILC系统框图

假定一般开环稳定系统的输出为:

yj(t)=Guj(t)+FL(t)

(6)

其中,G为被控对象;j为迭代次数;FL(k)为外部施加信号;t为时间变量。则系统的比例-微分(proportion-differentiation,PD)型迭代学习律为:

uj+1(t)=uj(t)+kpej+1(t)+kdej(t+1)

(7)

其中,kp、kd为迭代学习系数。

2.3 双迭代学习-交叉耦合控制

CCC方法能够有效提高多轴运动系统的轮廓跟踪能力,减小系统的轮廓误差,但是,该方法也存在一定的问题。一方面,其改进运动系统的轮廓跟踪能力与交叉耦合增益系数的精确程度密切相关,对于曲线加工轮廓精确计算增益系数是十分困难的;另一方面,CCC只是减小了轮廓误差,并没有改进单轴的跟踪误差[17]。而ILC则是一种无模型综合控制方法,对运动系统的数学模型和参数的精确度要求不严格,不需要很多的先验知识和计算量,并且能够有效提高跟踪性能。

基于上述控制方法的特点,本文结合反馈控制、单轴的ILC、双轴的CCC以及轮廓误差的ILC,提出了一种双迭代学习-交叉耦合控制(ILC&CCILC)的方法,其控制系统框图如图3所示。图3中,xr、yr分别为x、y轴的期望轨迹;Ex、Ey分别为x、y轴的期望轨迹和实际轨迹的误差;xj和yj分别为x、y轴的实际轨迹;ε为双轴运动系统的轮廓误差。

图3 ILC&CCILC系统框图

轮廓误差ε的迭代学习律为:

(8)

其中,kpε、kdε为轮廓误差的学习率。

x轴、y轴的迭代学习律分别为:

ux,j+1=[ux+(kpx+kdx)Ex-Cx(kpε+kdε)ε]j,

uy,j+1=[ux+(kpy+kdy)Ey+Cy(kpε+kdε)ε]j

(9)

其中,kpx和kdx、kpy和kdy分别为x、y轴的迭代学习系数。

由于Ex(t)=xr(t)-xj(t),Ey(t)=yr(t)-yj(t),将(6)式代入(9)式,可得:

(10)

其中

M11=I-[(kpx+kdx)+Cx(kpε+kdε)Cx]Gx;

M12=Cx(kpε+kdε)CyGy;

M21=Cy(kpε+kdε)CxGx;

M22=I-[(kpy+kdy)+Cy(kpε+kdε)Cy]Gy。

(11)

其中,i∈[1,n];λ为谱半径。由于max|λi|<1,收敛条件可以转化为:

(12)

3 仿真验证

为了验证ILC&CCILC方法对改善双轴运动系统的轮廓跟踪能力和降低单轴的跟踪误差的有效性,在Matlab/Simulink环境下建立模型并仿真。本仿真实验采用2台不同参数的永磁同步电机,电机的参数如下:Jx、Jy为5.8、1.4 kg;Bx、By为244.319 2、82.017 6 N·s/m,kfx、kfy为10.979 4、0.852 6 N/A。

本文采用双轴期望行切运动轨迹和螺旋线运动轨迹进行仿真验证,分别进行双轴交叉耦合-迭代学习控制(CCILC)仿真实验、双轴轮廓误差的CCC与单轴的ILC相结合的控制(ILC&CCC)仿真实验和ILC&CCILC仿真实验,比较3种控制方法的单轴跟踪误差和轮廓误差。不同的控制参数会使系统产生不同的误差,为了达到最好的控制效果,控制算法中的各个控制参数需要针对不同的控制对象和运动轨迹通过调试来确定。

3.1 行切运动仿真

进行行切运动轨迹仿真实验时,仿真时间t=6 s,采样周期为2 ms,学习周期为6 s。位置控制器参数kppx、kppy为35、45；速度控制器参数设置如下:kvpx、kvpy为150、180,kvix、kviy为2、2.5。行切运动轨迹的ILC&CCILC的PD型迭代学习律参数设置见表1所列,双轴期望行切运动轨迹如图4所示。

表1 行切运动轨迹的PD型迭代学习控制器参数

图4 双轴期望行切运动轨迹

3种控制方法的行切运动轨迹仿真结果如图5～8所示,其均方根误差见表2所列。由表2可知，进行行切运动时,ILC&CCILC和ILC&CCC控制方法的单轴跟踪误差都明显小于CCILC控制方法。ILC&CCILC 控制方法的x轴、y轴跟踪误差为ILC&CCC控制方法的79.88%、87.35%；ILC&CCILC 控制方法的轮廓误差分别为ILC&CCC和CCILC控制方法的82.38%和53.72%。。

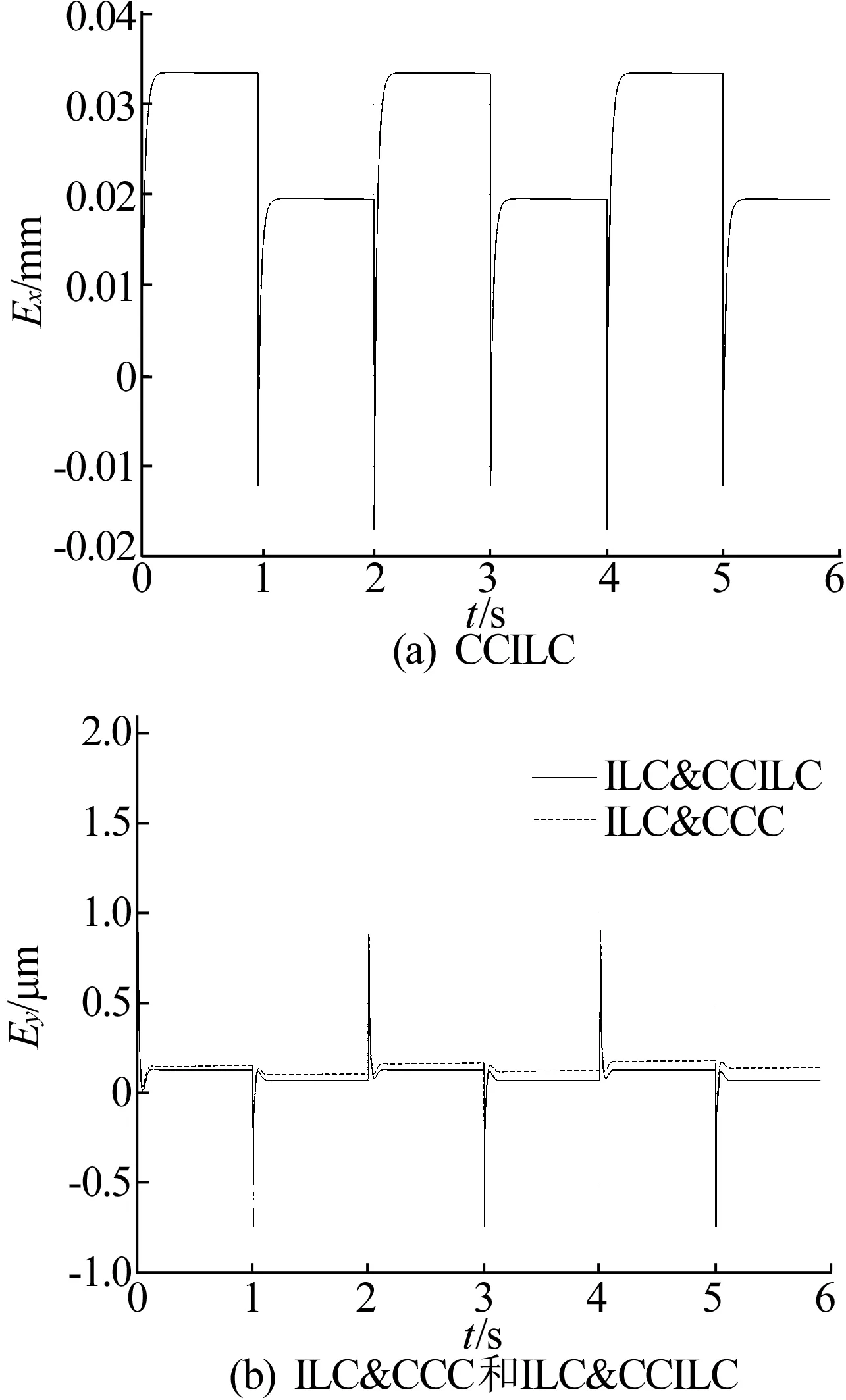
图5 行切运动轨迹3种控制方法的x轴跟踪误差

图6 行切运动轨迹3种控制方法的y轴跟踪误差

图7 行切运动轨迹3种控制方法的轮廓误差

图8 行切运动轨迹的最大轮廓误差绝对值与迭代次数的关系

3.2 螺旋线运动仿真

双轴期望螺旋线运动轨迹如图9所示。

图9 双轴期望螺旋线运动轨迹

螺旋线仿真实验时,仿真时间t=8 s,采样周期为2 ms,学习周期为8 s。取kppx、kppy为145、85；速度控制器参数设置如下:kvpx、kvpy为480、270,kvix、kviy为4.5、2。螺旋线轨迹方程为:x(t)=0.2tsin(4t),y(t)=0.2tcos(4t),t∈[0,8]。螺旋线运动轨迹的ILC&CCILC的PD型迭代学习律参数设置见表3所列。

表3 螺旋线运动轨迹的PD型迭代学习控制器参数

3种控制方法的螺旋线运动轨迹仿真结果如图10～13所示。其中,图10、图11、图12为第100次迭代学习时,单次执行螺旋线轨迹时的单轴跟踪误差和轮廓误差。

图10 螺旋线运动轨迹3种控制方法的x轴跟踪误差

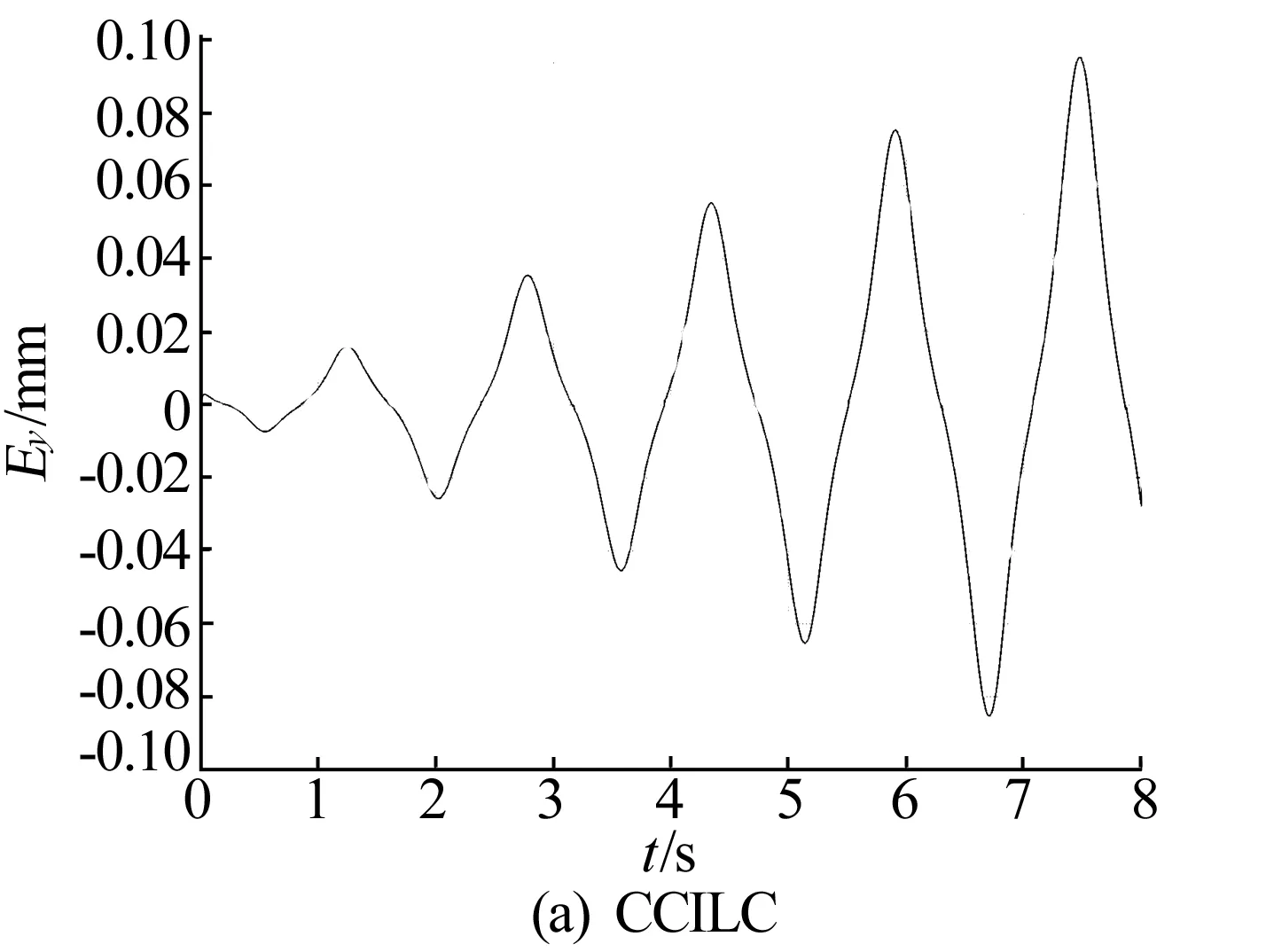
图11 螺旋线运动轨迹3种控制方法的y轴跟踪误差

图12 螺旋线运动轨迹3种控制方法的轮廓误差

图13 螺旋线运动轨迹最大轮廓误差绝对值与迭代次数的关系

螺旋线运动轨迹3种控制方法的均方根误差见表4所列。从表4可以看出,无论是单轴跟踪误差还是轮廓误差,ILC&CCILC和ILC&CCC控制方法都明显小于CCILC控制方法。ILC&CCILC控制方法的x轴、y轴跟踪误差为ILC&CCC控制方法的77.71%、78.25%,轮廓误差为77.68%。

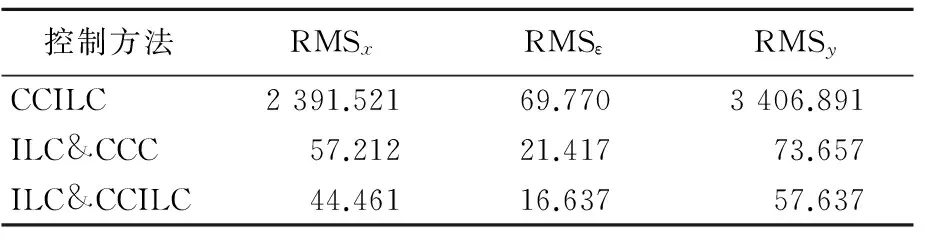
表4 螺旋线运动轨迹3种控制方法的均方根误差 nm

从图8可知,经过约60次迭代,行切运动最大轮廓误差绝对值可以减小到3×10-3mm左右;从图13可知,经过约50次的迭代,螺旋线运动轨迹最大轮廓误差绝对值可以削减到10-3mm左右。根据仿真结果,不同的运动轨迹迭代次数会有所不同,但轮廓误差均会在较少的迭代次数内收敛到一个很小的稳态值。目前随着控制器硬件性能快速提高,迭代运算会在极短的时间内运行完成,基本不会影响到算法的实际应用。

4 结 论

本文提出了一种基于双迭代学习-交叉耦合的双轴误差控制方法，仿真结果表明，无论是直线运动还是曲线运动,该方法都可以降低双轴运动系统的单轴跟踪误差,提高单轴的跟踪性能,同时也能增加各轴之间的匹配程度,显著减小运动系统的轮廓误差,提高轮廓加工精度。

[1] UCHIYAMA M.Formation of high speed motion pattern of mechanical arm by trial[J].Transaction of the Society of Instrumentation and Control Engineers,1978,14(6):706-712.

[2] LIN F J,HWANG J C,CHOU P H,et al.FPGA-based intelligent complementary sliding-mode control for PMLSM servo-drive system[J].IEEE Transactions on Power Electronics,2010,25(10): 2573-2587.

[3] 宋亦旭,王春洪,尹文生,等.永磁直线同步电动机的自适应学习控制[J].中国电机工程学报,2005,25(20):151-156.

[4] RAMESH R,MANNAN M A,POO A N.Tracking and contour error control in CNC servo systems[J].International Journal of Machine Tools & Manufacture,2005,45(3):301-326.

[5] KOREN Y.Cross-coupled biaxial computer control for manufacturing systems[J].Journal of Dynamic Systems Measurement and Control,1980,102(4):265-272.

[6] KOREN Y,LO C C.Variable-gain cross-coupling controller for contouring[J].Annals of the CIRP,1991,40(1):371-374.

[7] YEH S S,HSU P L.Theory and applications of the robot cross-coupled control design[J].IEEE Proceeding of American Control Conference,1997,1(3):791-795.

[8] SHIH Y T,CHEN C S,LEE A C.A novel cross-coupling control design for bi-axis motion[J].International Journal of Machine Tools and Manufacture,2002,42(14):1539-1548.

[9] CHIU G T C,TOMLIZUKA M.Contouring control of machine tool feed drive systems:a task coordinate frame approach[J].IEEE Transactions on Control Systems Technology,2001,9(1):130-139.

[10] 曲永印,赵希梅,郭庆鼎.基于零相位误差跟踪控制器的轮廓误差交叉耦合控制[J].中国机械工程,2006,17(11):1135-1137.

[11] 张代林,刘宇晗,杨吉祥,等.基于多层模糊控制的交叉耦合补偿方法的研究及应用[J].机械设计,2012(1):36-39.

[12] 王丽梅,庞月,杜帅，等.基于遗传算法的直驱XY平台变增益交叉耦合控制[J].沈阳工业大学学报,2011,33(5):481-485.

[13] 夏加宽,张琳娜，孙宜标，等.直线电机XY平台交叉耦合迭代学习控制[J].沈阳工业大学学报,2013,35(1):1-5.

[14] 张建国.基于滑模变结构控制的多轴协调运动控制策略研究[D].济南:山东大学,2007.

[15] 孙开珊.多轴空间轮廓误差的建模与交叉耦合补偿[D].武汉:华中科技大学,2007.

[16] 孙明轩,黄宝健.迭代学习控制[M].北京:国防工业出版社,1999.

[17] BARTON K L,ALLEYNE A G.A cross-coupled iterative learning control design for precision motion control[J].IEEE Transactions on Control Systems Technology,2008,16(6):1218-1231.

Dual-axiserrorcontrolbasedondouble-iterativelearningandcross-coupling

XU Wan, ZHENG Wei, YANG Wei, CAO Song, LUO Xi

(School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China)

In dual-axis high precision contour machining, the tracking errors of single axis load and the contour errors caused by the discordant motion of dual-axis have an influence on machining accuracy when processing parts. A dual-axis motion control strategy based on double-iterative learning and cross-coupling was proposed. The iterative learning control(ILC) of single axis and the dual-axis cross-coupled control(CCC) were combined with the ILC of contour errors. The tracking performance of single axis was improved by ILC of single axis, thus decreasing the tracking errors of single axis. The dual-axis CCC was used to increase the matching degree among axes, thus reducing the contour errors. The ILC of contour errors could improve the contour tracking performance. The simulation results indicate that the dual-axis motion control system based on double-iterative learning and cross-coupling can not only effectively decrease the tracking errors of single axis, but also significantly reduce the contour errors.

cross-coupling; iterative learning; contour error; tracking error; double-iterative learning and cross-coupling

2016-07-02；

2017-01-13

国家自然科学基金资助项目(51405144);湖北省自然科学基金面上资助项目(2014CF598)和湖北省科技支撑计划资助项目(2014BAA006)

许 万(1979-),男,湖北武汉人,博士,湖北工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.09.002

TP273. 22

A

1003-5060(2017)09-1158-07

(责任编辑 胡亚敏)