基于时频分析的粘接界面超声检测研究
2017-10-24常宁
常 宁
(中国人民武装警察部队学院基础部,河北廊坊 065000; 中国人民武装警察部队学院灭火救援技术公安部重点实验室,河北廊坊 065000)
基于时频分析的粘接界面超声检测研究
常 宁
(中国人民武装警察部队学院基础部,河北廊坊 065000; 中国人民武装警察部队学院灭火救援技术公安部重点实验室,河北廊坊 065000)
针对钢-橡胶粘接结构复合材料的粘接质量超声检测,提出了基于时频分析的定量分析算法。首先介绍了S变换和TT变换的原理,分析了TT变换的频谱特性,指出其具有高频放大作用;然后介绍了复合材料粘接质量超声检测的原理,分析了超声检测信号的特点;最后使用S变换和TT变换对超声检测信号进行处理,在时-频平面上提取出TT变换频谱对角线元素作为检测信号的特征参数。
S变换;TT变换;粘接质量;超声检测
0 引言
金属- 非金属粘接结构是复合材料中常见的一种,多用于航空航天、电子电器等高科技领域。但是粘接结构由于工艺控制不当或界面老化会造成粘接质量下降,有可能引起严重事故,因而对粘接质量的检测与评价已成为无损检测领域的一项重要内容[1][2]。目前,超声无损检测方法是复合材料粘接质量检测与评价的主要方法,其技术已经比较成熟,但仍然存在一些需要解决的难题[3]。文献[4]-[7]分别研究了采用不同技术和方法检测粘接质量,但都属于定性检测方法,定量检测方法还没有达到实际应用的要求。
S变换和TT变换是以傅里叶变换为基础的新的时频分析方法。S变换属于加窗可逆傅里叶变换,是以Morlet小波为基本小波的连续小波变换的延伸,其局部化特性良好,所以在信号处理等诸多领域得到了广泛应用。TT变换是Pinnegar于2003年提出的一维时间序列的二维实时表示方法,其时间局部分析能力很强,目前在机械故障检测等领域中应用广泛、效果良好[8]。
本文主要研究基于S变换和TT变换的复合材料粘接质量定量检测方法。超声检测回波信号属于时变信号,其中包含有丰富的高频信号分量,可以反映复合材料界面粘接状态。使用S变换和TT变换处理超声检测回波信号可以更好地提取其高频特征,克服傅里叶变换和小波变换等方法的不足[9][10]。
1 S变换与TT变换
S变换是傅里叶变换的一种改进方法,具有很好的时频定位能力[11]。通过S变换,一维时间信号可以被映射到二维时频平面,所以根据S变换矩阵,可以得到超声检测信号的频率信息及其与时间的对应关系[12]。
任意连续时间函数x(t)的S变换定义为:
(1)
式中,τ为控制高斯窗口在t轴位置的参数。由定义可以看出,S变换相当于信号加了宽度和高度可变的高斯窗函数后进行的傅里叶变换,因此其时间和频率分辨率都是可变的。
S逆变换的定义为:
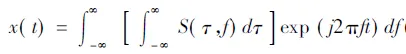
(2)
对S变换作傅里叶逆变换可得TT变换的表达式为

(3)
在区间τ内,TT变换的结果对于给定的t是一个局部化的时间函数,表示各个频率分量信号的幅值随时间变化的关系。TT变换的每一列都可以看作是一个TT序列。将TT(t,τ)按列求和即可得原信号,其表达式为

(4)
将式(1)代入式(3)中,并改变积分顺序,则可得TT变换的另外一种表达式为

(5)
其中

(6)
对(6)进行积分可得其解析表达式为
(7)
式中ε(·)为误差方程,表达式为
(8)
定义

(9)
则有
(10)
当t=τ时,在TT变换的对角线位置有

(11)
其中p(1)=-0.021 99。上式为卷积关系,根据傅里叶变换的时域卷积定理可得
TT(t,t)=F-1{X(f)G(f)}
(12)
式中,X(f)为信号x(t)的傅里叶变换,G(f)为信号g(t,τ)的对角线元素的傅里叶变换,由积分变换可得
G(f)=-2p(1)π2|f|
(13)
上式表明,G与|f|成正比,|f|越大,G越大,则TT(t,t)越大,即TT变换对角线元素值越大,所以TT变换矩阵在对角线附近的高频分量比低频分量的幅值更大。根据上述分析可知,TT变换可以突出信号的高频分量,有利于提取超声检测信号中的有用信息。
2 超声检测信号的时频分析
2.1 超声检测原理
本文所使用的超声检测对象是橡胶与不锈钢板粘接而成的复合薄板,其中橡胶厚度为5 mm,不锈钢板厚度为3 mm,粘接剂为环氧树脂胶粘剂。由于粘接剂涂抹不均而造成粘接界面脱粘是复合材料的主要缺陷。超声检测的目的是确定是否存在脱粘以及脱粘的程度,即对粘接质量进行定性及定量分析。
脉冲反射回波法是粘接质量的常用检测方法。由探伤仪产生脉冲波通过超声换能器垂直入射到钢板中,再由同一超声换能器接收粘接界面产生的回波信号。由于不锈钢和橡胶的声阻抗不同,超声波在粘接界面会产生反射。如果粘接质量良好,超声波在粘接界面的反射强度很小;如果存在脱粘,则超声波反射强度较大。对实际的超声检测信号进行分析,可以得到以下结论:⑴超声波信号会在不锈钢板中重复往返,总体回波信号是在某一时间段内若干次回波信号的叠加;⑵超声在不锈钢板中传播会产生能量反射,如果粘接质量越差,则反射能量越大,体现在波形上为回波幅度越大。因此,回波幅度大小能够反映粘接质量的好坏[13]。
2.2 超声检测信号的频谱特性分析
根据上述对于超声检测信号的分析可知,总的回波信号是由若干次回波叠加而构成。由于受到超声信号在钢板中传播时间的影响,每次回波信号都会发生相位畸变,总的回波信号会在叠加起始点处产生幅值突变。根据信号的频谱分析理论,时域信号的幅值突变对应信号频谱的高频分量。因此,从超声检测信号中提取高频分量可以作为判断粘接质量的依据。
一般情况下,信号的频谱中低频分量占主要成分,而基于傅里叶变换的频谱分析方法由于信号的截断而造成频谱泄露,高频分量部分很可能被低频分量淹没而无法提取。根据分析可知,TT变换可以将高频分量凸显出来,同时可以确定高频分量的起始时间,有利于超声检测信号特征的分析。
首先对超声检测信号进行S变换以确定信号的时频分布特性。对脱粘率分别为30%和50%的粘接界面超声检测信号进行S变换,得到的时频分布见图1和图2所示。由S变换的结果可知,随着脱粘率的增大,超声检测信号的频谱在时域扩展的越严重,说明粘接质量越差,界面反射的回波越多,与上述理论分析的结果吻合。然而由于受S变换的时间和频率分辨率的限制,各频率分量的起止时间、幅度和频率等参数都会存在一定的误差。另外,由于数据截断造成的频谱泄露使得S变换产生虚假频率成分,因此所得频谱在频域展宽严重,不利于对超声检测信号频谱特征的提取。

图1 超声信号的S变换频谱
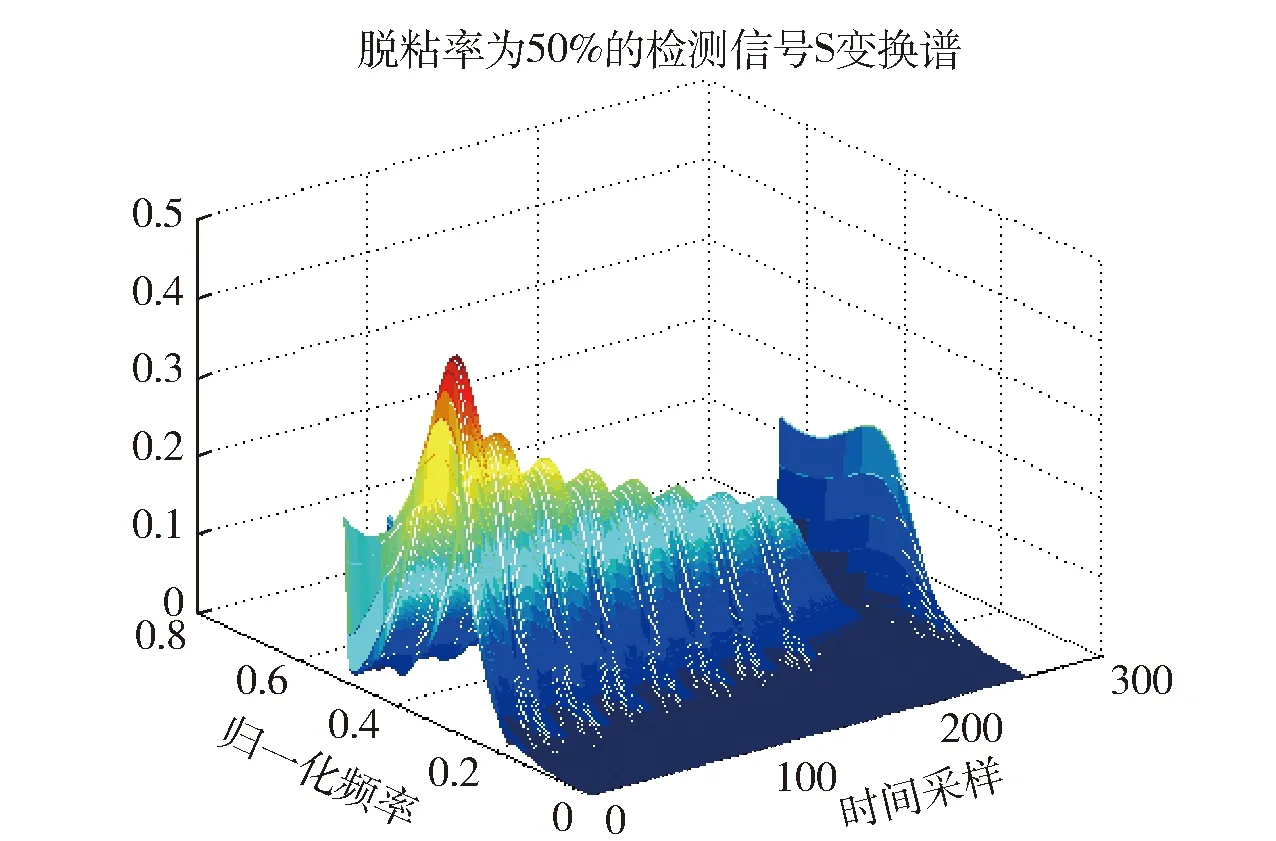
图2 超声信号的S变换频谱
TT变换在对角线及其附近位置对高频信号具有很强的聚集能力,不同频率点处的频谱分布范围很窄,完全可以克服S变换带来的频谱展宽和虚假频率分量的问题,有利于对超声检测信号特征的分析。因此在S变换的基础上进一步对超声检测信号进行TT变换,结果见图3所示。对TT变换对角线元素作傅里叶变换的结果见图4所示。由图3和图4可知,随着脱粘率的增加,超声检测信号的高频分量增多,且幅度较大,可以作为判断粘接质量的依据。

图3 超声检测信号TT谱
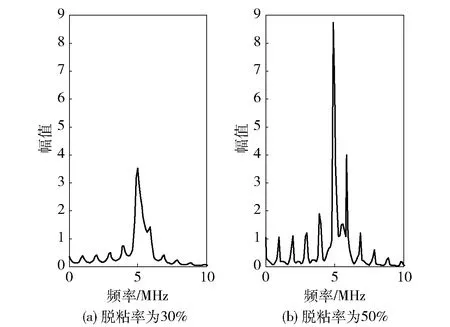
图4 超声检测信号频谱
3 结语
本文提出了利用S变换和TT变换对复合材料粘接质量超声检测信号进行处理以提取特征参数的方法。该方法主要利用TT变换可以对信号的高频分量进行聚焦的特性,可以有效地提取出超声检测信号所携带的有关界面粘接质量的特征信息,可以为粘接质量的定量识别提供依据。
[1] 李明轩.粘接质量超声检测研究[J].应用声学,2002,21(1):6-12.
[2] 武翠琴,洪新华,王卫平,等.复合材料脱粘缺陷的红外热像无损检测[J].强激光与粒子束,2011,23(12):3272-3274.
[3] 李明轩,王小民,安志武.粘接界面特性的超声检测与评价[J].应用声学,2013,32(5):190-198.
[4] 安志武,王小民,毛捷,等.粘接件拉伸强度的超声检测实验研究[J].声学学报,2011,36(4):384-388.
[5] 樊森,王召巴,金永,等.发动机绝热层粘接质量超声自动检测系统设计[J].宇航学报,2010,31(6):1646-1650.
[6] 艾春安,刘瑜,李剑,等.基于经验模态分解的粘接结构缺陷定量缺陷[J].玻璃钢/复合材料,2012(6):3-7.
[7] 常新龙,尼涛,艾春安,等.脱粘缺陷对粘接结构频散特性的影响[J].应用声学,2010,29(3):227-235.
[8] 黄纯,朱智军,曹一家,等.一种电网谐波与间谐波分析新方法[J].电工技术学报,2013,28(9):32-38.
[9] 高志奇,陈振清.基于小波变换和RBF网络的薄板粘接质量评价研究[J].内蒙古工业大学学报,2011,30(4):506-510.
[10] 谢常欢,何湘铂,陈国华.小波分析在裂纹型缺陷超声无损定量检测中的应用研究[J].压力容器,2005,22(4):5-9.
[11] 满蔚仕,张志禹,康青,等.利用快速S变换的电能质量扰动识别方法[J].西安交通大学学报,2013,47(8):133-140.
[12] 魏莹莹,安庆龙,蔡晓江,等.碳纤维复合材料超声扫描分层检测及评价方法[J].航空学报,2016,37(11):35123-519.
[13] 高志奇.复合材料粘接质量评价方法研究[J].内蒙古工业大学学报,2012,31(3):32-36.
(责任编辑陈小明)
TB302
常 宁(1975—),男,内蒙古临河人, 副教授,硕士。研究方向为电子科学与技术及安全科学与技术。
