强衰减条件下能量比法的修正及其应用
2017-10-23王晓涛毛海波
王晓涛 谭 佳 毛海波 蒋 立
(中国石油新疆油田公司勘探开发研究院地球物理研究所,新疆乌鲁木齐830013)
强衰减条件下能量比法的修正及其应用
王晓涛*谭 佳 毛海波 蒋 立
(中国石油新疆油田公司勘探开发研究院地球物理研究所,新疆乌鲁木齐830013)
吸收衰减是引起地震波能量损失的一个重要因素,尤其是在近地表强衰减条件下。常规的能量比法是利用地震波能量的线性衰减速率定量估测品质因子Q,不适用于近地表的强衰减(Q小于30)情况;修正的能量比法利用地震波能量的指数衰减速率估算Q值,减小了常规方法的理论误差,适用于近地表条件。仿真模型和实际资料处理结果表明,在非固有衰减(主要为几何扩散)得到较好补偿的前提下,修正能量比法估算的近地表Q值合理、可靠,具有实用性。
能量比 品质因子Q近地表 指数衰减
1 引言
地层介质的吸收作用导致地震波在传播过程中能量发生衰减,且还引起主频降低、相位改变等,严重影响了中深层地震资料的构造成像能力和储层预测精度[1,2]。品质因子Q是描述介质吸收衰减强弱的参量,也是吸收补偿、流体检测的重要依据[3]。因吸收衰减造成地震子波的某些特征发生变化,故基于不同的特征变化可形成不同的Q值估算方法。例如,基于子波的最大振幅变化形成振幅衰减法[4];基于瞬时频率的变化产生了解析信号法[5];基于子波波长增宽造就了上升时间法[6];基于子波谱振幅的指数衰减得到对数谱比法[7];基于子波谱主频的降低建立了质心频移法[8-16]或峰值频率法[17-19];基于子波能量的衰减诞生了能量比法[20]。
上述各类方法并不存在明显的优劣,关键在于针对不同的资料选择适用的方法。近地表品质因子一般小于30,如在中国西部沙漠地区,当低速带和降速带较厚(几十米)时,对地震波的吸收衰减作用较强,造成的能量损失较大,甚至超过几何扩散损失,则此时宜采用能量比法实现近地表的Q值估算。但常规能量比法存在一定的理论近似,且在强衰减情况下可能存在较大误差[20]。因此,在应用能量比法之前,需对该方法做理论修正和模型测试,以增强其有效性和实用性。
2 基本原理
记初始地震子波为A1(f),相应总能量为E1,均匀介质品质因子为Q,传播时间为t,衰减后地震子波为A2(t),相应总能量为E2,则有如下关系
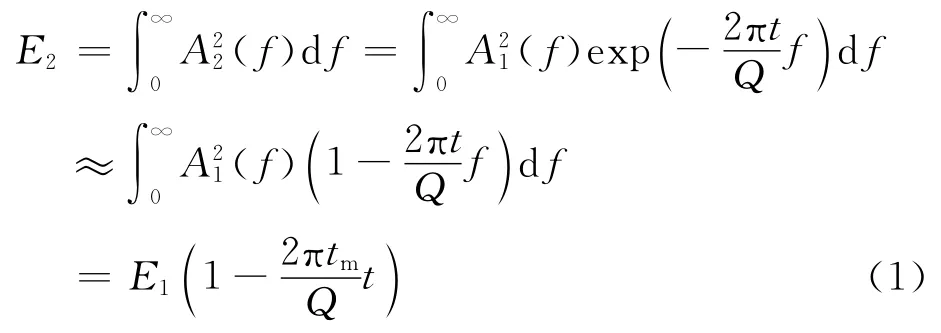
式(1)中的近似处理使其只能适用于吸收衰减相对较弱的情形,即2πftQ-1<0.2,不适用于强衰减条件的近地表。进一步研究发现,可对式(1)做修正近似

式(1)与式(2)的区别在于,前者表明地震波传播过程中地震子波的能量随时间呈线性衰减,后者表明衰减过程中能量呈指数衰减。笔者认为:在衰减较弱的情况下,式(1)与式(2)区别不大;在衰减较强的情况下,式(2)的理论精度比式(1)高。原因有两点:首先,如果式(1)的近似处理产生了正(或负)的误差,那么式(2)的近似处理将相应产生负(或正)的误差,恰好抵消了第一次近似带来的一部分误差,提高了理论精度;其次,当传播时间足够长时,根据式(1)估算的能量将产生负值,而根据式(2)估算的能量恒为正值,相比之下,式(2)的结果更符合物理意义。
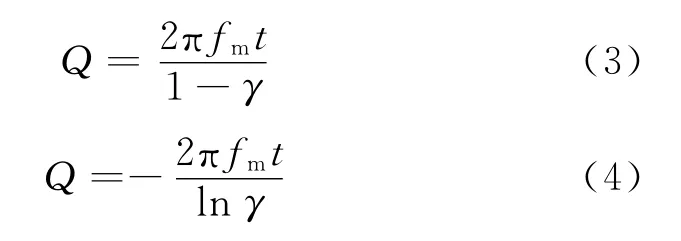
据Q值的定义可得
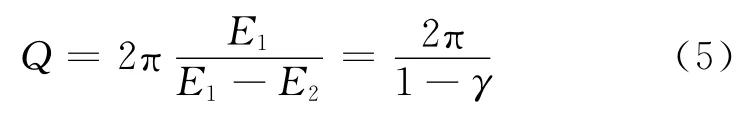
从形式上看,式(3)与式(5)相近,但两者存在本质差别,即式(5)是在地震波传播1个波长的假设下成立。不难看出:当研究对象是单频波且传播距离正好为1个波长时,式(3)中的fmt=1,与式(5)完全等价。而实际地震波是由多个频率成分组成,传播一个周期后,fmt=1并不一定成立,且式(3)和式(4)研究的条件是地震波传播任意时间,与式(5)的假设条件不同。当传播时间较小时,吸收引起的能量衰减还不够强(即γ→1,lnγ≈γ-1),式(3)与式(4)的结果近似相等;当传播时间较长时,吸收引起的能量衰减较强,式(3)和式(4)将会出现明显的差异。假设t足够大,为了保证估算的地层Q值恒定不变,式(3)中的分母1-γ需要与t同步增大,则γ有可能变为负值,而式(4)分母中的-lnγ在γ>0时能实现与t同步增大,因此,式(4)比式(3)更客观、更合理。
3 模型测试
3.1 能量衰减
通过测试衰减条件下的地震波能量衰减规律,验证式(1)和式(2)。模拟近地表的激发条件,取主频为70 Hz的Ricker子波为初始地震子波,0.1ms采样。由于Q值和传播时间t都是影响能量的参量,这里将作为一个变量,记为β(单位为s),考察地震波能量比γ随参量β的变化规律。图1a是地震波吸收衰减前后的能量比值γ与参量β的关系图。对比图中三条曲线发现:当β<0.2ms时,三者吻合度较高,线性衰减式和指数衰减式均具有较高精度,即在该区间段两式等价;当β>0.2ms时,三者开始出现偏差,指数衰减曲线与真实测量值趋势一致,线性衰减曲线偏离真实值,且随着β的增大,误差逐渐增加。类似的对比见图1b,其初始地震子波是主频为150 Hz的Ricker子波,可见线性衰减式(红线)与理论值(蓝线)的误差更大,甚至当β>1ms时,能量比出现没有物理意义的负值,指数衰减式(紫线)的误差在可接受范围内。因此,指数衰减式(2)比线性衰减式(1)具有更高的理论精度。
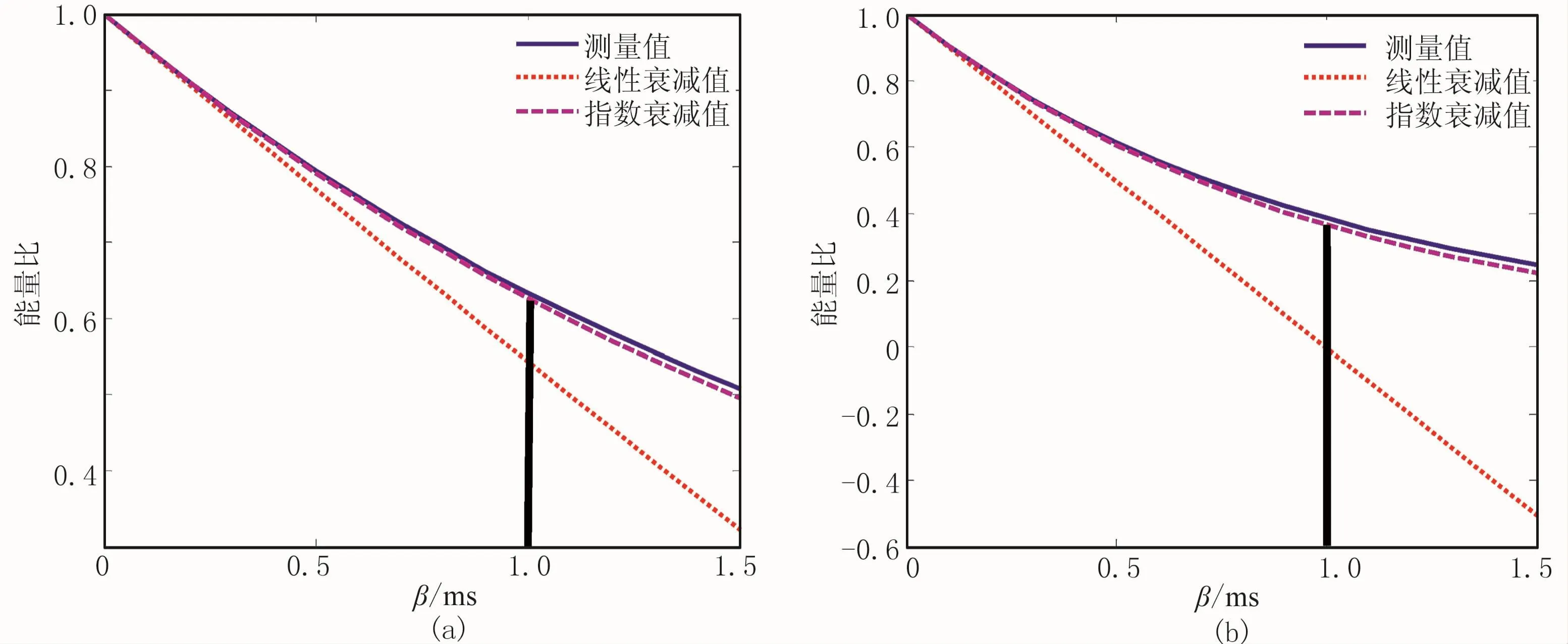
图1 地震波吸收衰减前后的能量比与β的关系
图1对于实际应用有重要指导意义。做一个简单估算:假设近地表风化层Q值取10,厚度为5m,速度为500m/s,垂直地面激发接收,单程旅行时为10ms,则β=1ms,对应图1中黑线所示位置,线性衰减式存在较明显的误差,因此能量比法的改进对近地表Q值估算很有必要。
3.2 Q值估算
模拟近地表的激发接收条件,取主频为70Hz的Ricker子波为初始地震子波,0.1ms采样。假设地震子波从离震源10m处传播到20m处,经过的介质速度为500m/s,传播时间为20ms,Q值取20。图2是衰减前(蓝线)、后(红线)的地震子波的波形及频谱图,为便于对比,地震子波已做零相位化和几何扩散补偿处理(下同)。从波形图看出,衰减地震子波的振幅存在较明显的降低,总能量衰减为原来的67.52%;从频谱图可知,主频由原来的74.47Hz衰减为70.93Hz。将以上测量参数代入式(3)和式(4),则估算的Q值为24.92和20.00,相对误差为24.59%和2.22%。
与此类似,图3中选取主频为150 Hz的Ricker子波作为初始子波,子波能量衰减为原来的38.59%,主频由原来的159.58 Hz衰减为143.81 Hz,估算的Q值分别为32.66和21.06,相对误差为63.28%和5.31%。对比结果表明:与常规能比法相比,修正的能比法更适用于强衰减近地表条件。
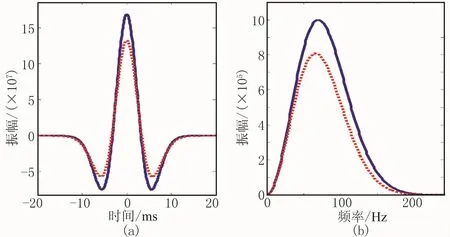
图2 主频为70Hz地震子波衰减前(蓝)、后(红)的波形(a)及其频谱(b)
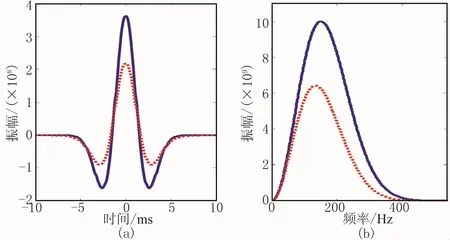
图3 主频为150 Hz地震子波衰减前(蓝)、后(红)的波形(a)及其频谱(b)
4 实际资料应用
实际数据选自中国西部沙漠地区,其近地表的低速带和降速带较厚(达几十米甚至上百米),对地震波的吸收衰减作用较强。图4a是工区某测量点的双井激发接收系统(俯视)示意图,在激发井的不同深度用雷管进行震源激发,两井间距为6.5m,井中布设4个检波器,其余检波器沿两井连线及其垂直方向埋置于地面。图4b是根据激发井口检波器接收记录划分的低速带和降速带,其中低速带厚度为12m,速度为628m/s,降速带厚度为88m,速度为1190m/s。
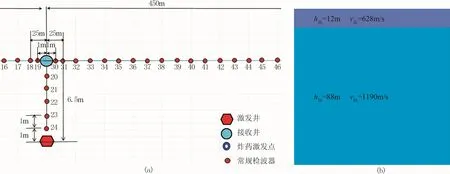
图4 双井激发接收系统(a)及井旁近地表模型(b)
图5是地表检波器接收的不同炮检距(检波器与激发井口的距离)共检波点道集,在激发深度约78m处,有一未响应坏道。图6是根据近地表速度模型(图4b)正演的传播路径(图6a)和分层走时(图6b)。利用图6a的传播路径对图5中的共检波点道集分别做几何扩散补偿,并提取两个道集的初至波能量比值曲线(图7a)。将能量比值和分层旅行时代入式(4),反演得到图7b所示的近地表Q值曲线。由于能量比法对于地震信号的保幅性处理要求较高,容易受非固有衰减(如几何扩散、反射透射损失等)补偿不彻底、复合波干扰等因素影响,从图7b得到的仅是近地表Q值的大致趋势,其相邻测量点之间的局部跳动(尤其是深部的大幅度变化)并不一定是地表介质的真实反映。因此,对图7b中的Q值曲线在低速带和降速带分别取平均,求得低速带Q值为6.73,降速带Q值为14.22。该做法虽然纵向分辨率不够高,但可得到相对稳定可靠的结果。
作为对比,在该测量点同时采用频谱比法估算近地表Q值,所选资料对应的炮点深度分别为3、10、20、35、50、62和85m。在低速带中激发,激发深度为3m(图8),从其不同炮检距的检波器接收的初至波频谱图(图8a)可看出,能量和主频具有较大的变化;分析其对数谱比曲线(图8b),根据拟合斜率估计的Q值为7.07。在降速带中激发,激发深度为62m(图9),得到不同炮检距的检波器接收的初至波频谱图(图9a)和对数谱比曲线(图9b),根据拟合斜率估计的Q值为11.29。图7b中的红点是利用谱比法估计的Q值,对比可知能量比法与谱比法估算的品质因子在数值上较为接近,表明能量比法估算的Q值能大致反映近地表介质的平均水平。
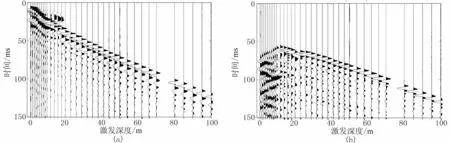
图5 地表接收的不同炮检距(a,1m;b,25.02m)共检波点道集
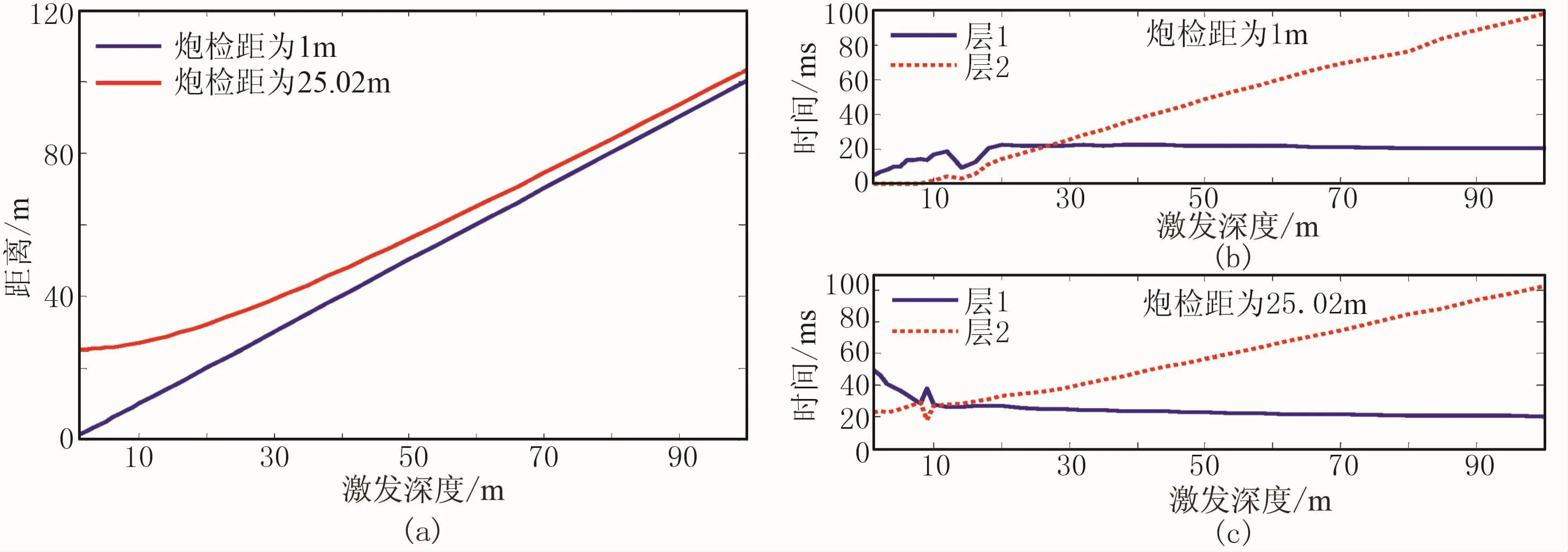
图6 根据图4b速度模型正演的传播路径(a)和不同炮检距的分层走时(b、c)

图7 能量比曲线(a)及应用能量比法和频谱比法反演的Q值(b)
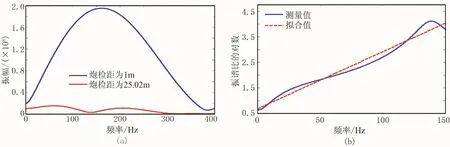
图8 低速带中激发时不同炮检距的检波器接收初至波的频谱(a)和对数谱比曲线(b)
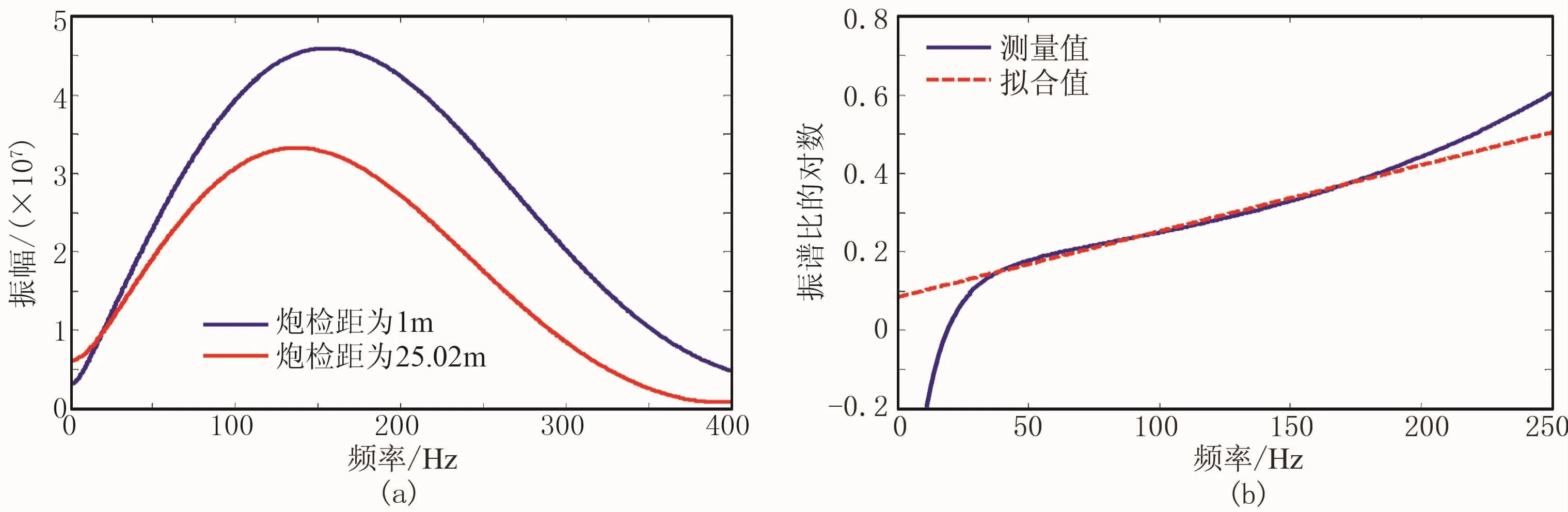
图9 降速带中激发时不同炮检距的检波器接收初至波的频谱(a)和对数谱比曲线(b)
采用质心频移法,对区内已开展过近地表调查的多个观测点进行了Q值估算。图10是工区近地表的Q值与速度散点图,其中蓝圈是邻近多个观测点的Q值(基于质心频移法),红框是本文展示的观测点Q值(基于能量比法),通过拟合得到该工区的Q-v经验式:Q=13.30v2.14。可见能量比法估算的Q值基本落在合理区间,具有一定的可信度。
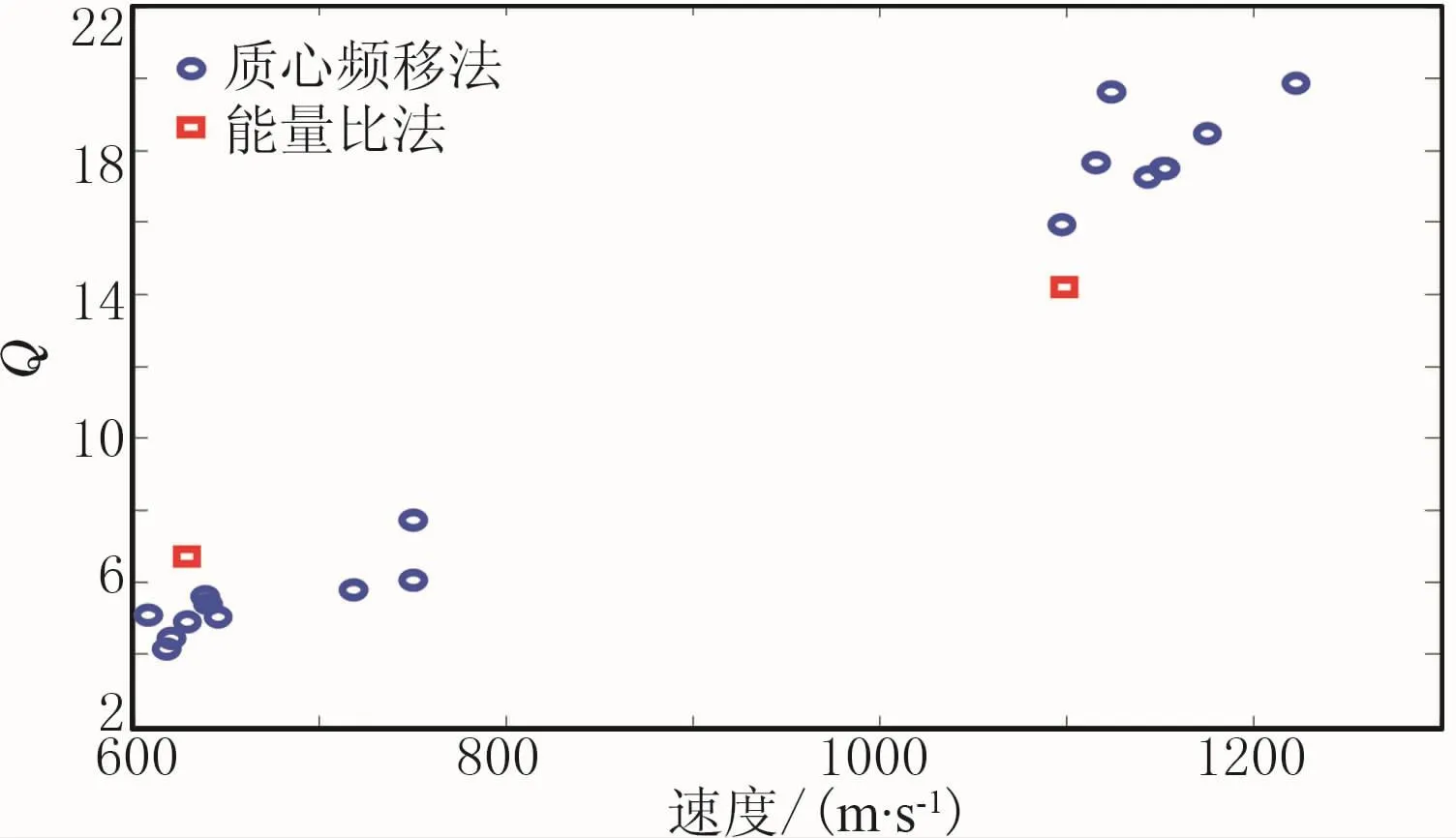
图10 Q-v散点图
5 结束语
常规能量比法认为吸收衰减造成的地震波能量与传播时间呈线性关系,改进的能量比法则将线性关系校正为指数关系。当吸收衰减作用较弱时,这两种方法基本是等价的,且均具有较高精度;当吸收衰减较强时,测试结果更倾向于指数衰减(即修正的能量比法)。因此,在强衰减近地表条件下,宜采用修正的能量比法。模型仿真和实际应用结果均验证了该方法的可行性和适用性。需要强调的是,道集数据的前期保幅处理(主要是几何扩散补偿、干扰压制等)质量直接影响该方法的应用效果。
[1] 马昭军,刘洋.地震波衰减反演研究综述.地球物理学进展,2005,20(4):1074-1082.Ma Zhaojun,Liu Yang.A summary of research on seismic attenuation.Progress in Geophysics,2005,20(4):1074-1082.
[2] 李金丽,李振春,管路平等.地震波衰减及补偿方法.物探与化探,2015,39(3):456-465.Li Jinli,Li Zhenchun,Guan Luping et al.The method of seismic attenuation and energy compensation.Geophysical and Geochemical Exploration,2015,39(3):456-465.
[3] 严红勇,刘洋.地震资料Q值估算与反Q滤波研究综述.地球物理学进展,2011,26(2):606-615.Yan Hongyong,Liu Yang.A summary of research on estimation ofQand inverseQfiltering for seismic wave.Progress in Geophysics,2011,26(2):606-615.
[4] Ward R W,Young C Y.Mapping seismic attenuation within geothermal systems using teleseisms with application to the Geysers-Clear Lake region.Journal of Geophysical Research,1980,85(B10):5227-5236.
[5] Engelhard L.Determination of seismic-wave attenuation by complex trace analysis.Geophysical Journal International,1996,125(2):608-622.
[6] E Kjartansson.ConstantQ-wave propagation and attenuation.Journal of Geophysical Research,1979,84(B9):4737-4748.
[7] Hauge P S.Measurements of attenuation from vertical seismic profiles.Geophysics,1981,46(11):1548-1558.
[8] Quan Y L,Harris J M.Seismic attenuation tomography using the frequency shift method.Geophysics,1997,62(3):895-905.
[9] 高静怀,杨森林,王大兴.利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子.地球物理学报,2008,51(3):853-861.Gao Jinghuai,Yang Senlin,Wang Daxing.Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data.Chinese Journal of Geophysics,2008,51(3):853-861.
[10] Hu W Y,Jonathan L,Bear L et al.A robust and accurate seismic attenuation tomography algorithm.SEG Technical Program Expanded Abstracts,2011,30:2727-2731.
[11] 赵宁,曹思远,王宗俊等.频域统计性属性组合提取品质因子Q.石油地球物理勘探,2013,48(4):545-552.Zhao Ning,Cao Siyuan,Wang Zongjun et al.SeismicQestimation by combinations of frequency statistics attributes.OGP,2013,48(4):545-552.
[12] 王宗俊,范廷恩,马淑芳等.地震波质心频率变化规律.石油地球物理勘探,2015,50(5):861-872.Wang Zongjun,Fan Ting’en,Ma Shufang et al.Variation characteristics of seismic wavelet centroid frequency.OGP,2015,50(5):861-872.
[13] 余连勇,范廷恩,胡光义等.时间域质心频移法估算品质因子Q.西南石油大学学报(自然科学版),2014,36(4):55-62.Yu Lianyong,Fan Ting’en,Hu Guangyi et al.Estimating quality factorQwith time-domain centroid frequency shift method.Journal of South-west Petroleum University:Science & Technology Edition,2014,36(4):55-62.
[14] 王宗俊.基于谱模拟的质心法品质因子估算.石油物探,2015,54(3):20-26.Wang Zongjun.Quality factor estimation by centroid frequency shift of spectrum fitting.GPP,2015,54(3):20-26.
[15] 李君君,王志章,张枝焕等.质心频率线性拟合法估算品质因子Q.石油地球物理勘探,2015,50(2):254-259.Li Junjun,Wang Zhizhang,Zhang Zhihuan et al.Estimation of quality factorQbased on linear fitting of centroid frequency curve.OGP,2015,50(2):254-259.
[16] 白利娜,赵凌云.时间域属性组合法提取品质因子Q.石油地球物理勘探,2015,50(3):436-443.Bai Lina,Zhao Lingyun.Quality factor extraction with an attribute combination method in the time domain.OGP,2015,50(3):436-443.
[17] Zhang C,Ulrych T J.Estimation of quality factors from CMP records.Geophysics,2002,67(10):1542-1547.
[18] 高静怀,杨森林.利用零偏移VSP资料估计介质品质因子方法研究.地球物理学报,2007,50(4):1198-1209.Gao Jinghuai,Yang Senlin.On the method of quality factors estimation from zero-offset VSP data.Chinese Journal of Geophysics,2007,50(4):1198-1209.
[19] Tu N,Lu W K.An improved peak-frequency-shift method forQestimation.CPS/SEG International Geophysical Conference& Exposition,Beijing,2009,1218.
[20] Wang Z J,Cao S Y,Zhang H R et al.Estimation of quality factors by energy ratio method.Applied Geophysics,2015,12(1):86-92.

P631
A
10.13810/j.cnki.issn.1000-7210.2017.01.007
王晓涛,谭佳,毛海波,蒋立.强衰减条件下能量比法的修正及其应用.石油地球物理勘探,2017,52(1):42-47.
1000-7210(2017)01-0042-06
*新疆乌鲁木齐市中国石油新疆油田公司勘探开发研究院地球物理研究所,830013。Email:wxiaotao@petrochina.com.cn
本文于2016年1月22日收到,最终修改稿于同年12月16日收到。
(本文编辑:朱汉东)
王晓涛 工程师,1982年生;2007年本科毕业于西南石油大学勘查技术与工程专业;2010年获该校地球物理探测与信息技术专业硕士学位;现在中国石油新疆油田公司勘探开发研究院地球物理研究所主要从事地震数据处理及其方法研究。
