消声器传递损失计算的单元能量叠加法
2017-10-23王世华季振林
王世华,季振林
(哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001)
消声器传递损失计算的单元能量叠加法
王世华,季振林
(哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001)
在消声器进出口管道平面波截止频率以上,高阶模态被激发,传统方法假设进出口为平面波计算消声器传递损失的方法已不再适用。基于有限元法,把进出口面划分出若干个单元,将每个单元上的声场分布近似为平面波,建立基于单元能量叠加计算消声器传递损失的方法,并使用本文方法和Virtual.Lab Acoustics软件计算了三种类型消声器的传递损失,分析了非平面波现象。结果表明,本文方法可行且能够有效地考虑非平面波的影响。
声学;消声器;传递损失;非平面波;有限元法;单元能量叠加
消声器是控制进排气噪声的有效装置,为设计性能优良的消声器,需要采用有效方法计算并分析其消声性能[1–2]。传统方法预测消声器的声学性能时,需要假设消声器进出口管道内为平面波,在计算频率较低时,这种假设是合理的。然而,当计算频率超过进出口管道的平面波截止频率时,高阶模态在进出口管道内可以传播,此时声场已不再是平面波。本文研究的目的是建立一种计算消声器宽频传递损失的方法。基于有限元法,结合进出口单元能量叠加法,建立了能够考虑进出口管道内非平面波影响的消声器传递损失计算方法,通过与Virtual.Lab Acoustics管道声模态法计算得到的传递损失结果比较验证了本文方法的正确性,进而分析了非平面波效应。
1 理论方法
1.1 声学有限元方程
消声器内声场的控制方程为[2]

将声学域离散成有限个单元,单元内任意一点的声压值可以用该点所在单元上所有节点声压表示,即

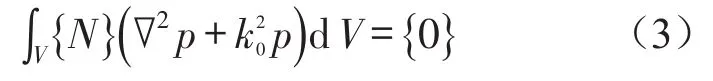
应用高斯公式可得[3–4]
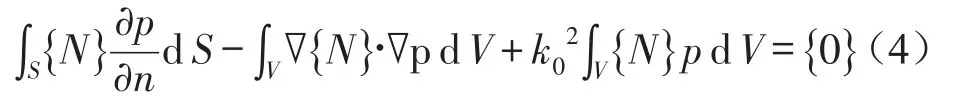
将(2)式代入(4)式得
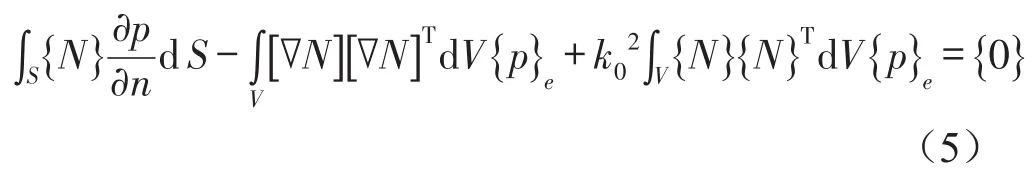
其中S为边界表面,可分为刚性壁面Sw、进口面Si、出口面So,相应的边界条件分别为
(a)刚性壁面边界条件

(b)进口速度边界条件
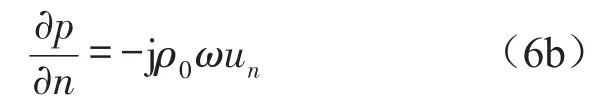
(c)出口无反射边界条件

将式(6)代入式(5)整理得
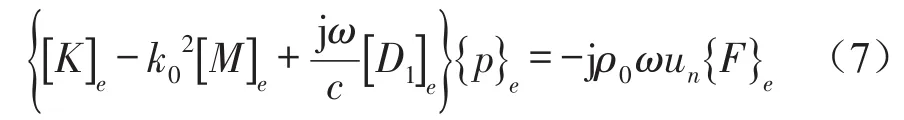
其中
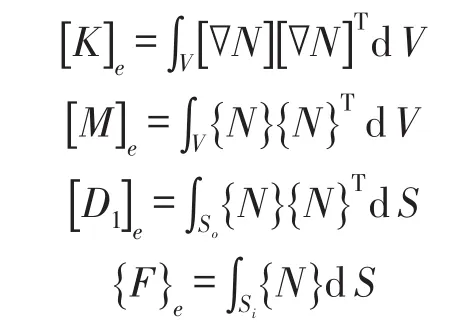
结合边界条件,求解方程(7)就可以得到各个单元节点上的声压值。
1.2 传递损失的计算
消声器的传递损失定义为进口处入射声功率级与出口透射声功率级之差,可表示为[2]
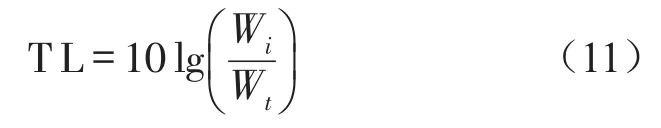
其中Wi和Wt分别为消声器进口处入射声功率和出口处透射声功率。
将进出口面离散成有限个单元,如图1所示。
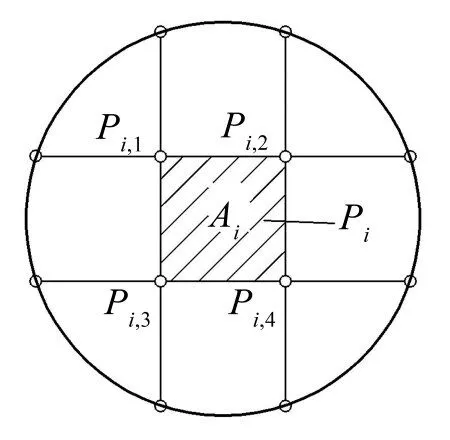
图1 进出口面单元划分示意图
若每个单元面积Ai较小时,每一个单元上声场分布可以近似看成平面波。在消声器进出口处分别给定质点振速边界条件和无反射边界条件后,每个单元上的平均声压值pi可以用该单元上所有节点声压值计算得到。进出口面上第i个单元的面积和平均声压可以表示为
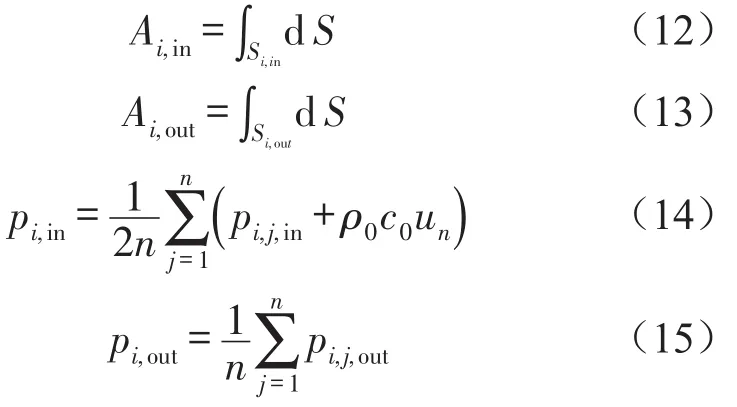
其中Si,in和Si,out为进出口面上第i个单元的表面;Ai,in和Ai,out分别为进出口面上第i个单元的面积;pi,in和pi,out为进出口面上第i个单元上的平均入射声压值和平均透射声压值;pi,j,in和pi,j,out为进出口面上第i个单元上第j个节点的声压值;n为单元的节点个数。
将上式代入(11)式,则传递损失可以表示为
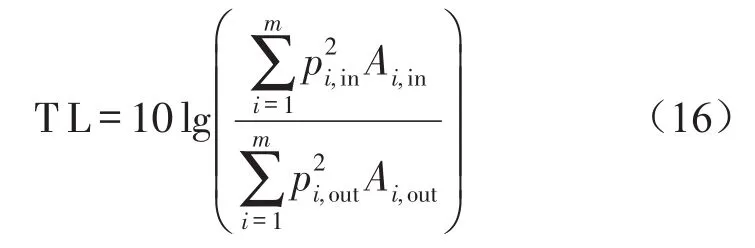
其中m为进出口面上划分的单元个数。显然,计算精度与进出口面上划分单元的个数有很大关系。当进出口管道截面上划分单元的个数较多时,每个单元的截面就会越小,在每个单元上的声压分布就会越接近平面波,计算精度就会越高。
1.3 管道声模态法
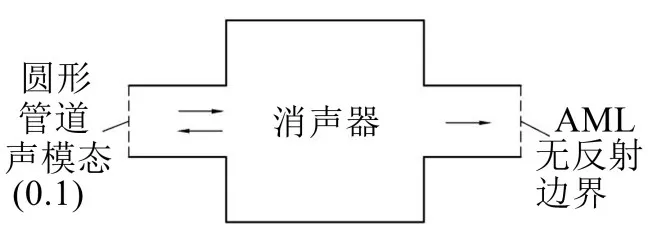
图2 消声器声模态法计算示意图
对于进出口管道为圆形的消声器,在Virtual Lab Acoustics软件中能够利用管道声模态方法计算传递损失。如图2所示,在利用圆形管道声模态计算消声器的传递损失时,通常消声器进口处定义为(0,1)阶管道声模态激励,消声器出口处定义为AML(Automatic Matched Layer)无反射边界条件。这种方法的优势是采用了AML技术,能够对无反射边界实现更优的模拟[5]。
2 计算实例与分析
考虑如图3所示的膨胀腔消声器,膨胀腔内径D=800 mm,膨胀腔长度L=400 mm,进出口管直径d1=300 mm,d2=300 mm,进出口插管长度分别为L1=150 mm,L2=100 mm,壳体壁厚tw=2 mm。声速为c0=343 m/s。
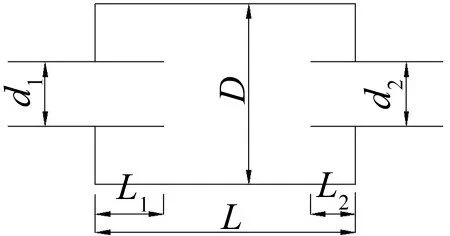
图3 进出口插管消声器示意图
图4比较了用管道声模态法与本文方法计算得到的传递损失结果。该消声器的进出口管道平面波截止频率大约在1 400 Hz左右,从图可以看出,在截止频率以下,两种方法计算结果吻合较好。在截止频率以上,两者计算结果存在一定偏差,本文方法计算出的传递损失曲线共振峰明显多于用管道声模态法计算结果的共振峰。

图4 进出口插管消声器的传递损失
为了消除共振峰产生的影响,在原模型基础上添加100 g/L玻璃丝棉,为保护吸声材料使用了穿孔管,形成了穿孔管阻性消声器,如图5所示,其中,穿孔板壁厚tw=2 mm,穿孔孔径dh=5 mm,穿孔率为ϕ=25%。
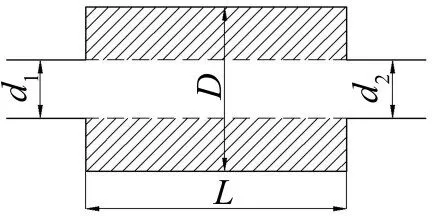
图5 穿孔管阻性消声器示意图
图6比较了用管道声模态法与本文方法计算穿孔管阻性消声器的传递损失结果。可以看出,两者传递损失曲线整体吻合较好,说明了文中方法是可行的。但在截止频率以上,两者结果仍然存在一些差异,用管道声模态法计算的传递损失曲线趋势较平缓;而本文方法计算的传递损失曲线略有波动,还出现了两个明显的共振峰。
为了进一步观察非平面波效应,首先采用传统方法使用Virtual.Lab Acoustics计算如图7所示的阻抗复合式消声器的传递损失。消声器具体尺寸为:d1=d2=700 mm,D1=1 300 mm,D2=1 200 mm,L1=200 mm,L2=300 mm,L3=400 mm,L4=200 mm,L5=200 mm,L6=300 mm,L7=1 200 mm,L8=800 mm,L9=1 000 mm,穿孔板壁厚tw=2 mm,穿孔孔径dh=5 mm,穿孔率ϕ=25%。声速为c0=520 m/s,进出口管道平面波截止频率约为900 Hz。
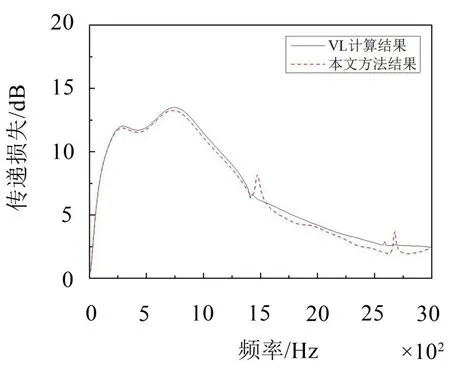
图6 穿孔管阻性消声器的传递损失
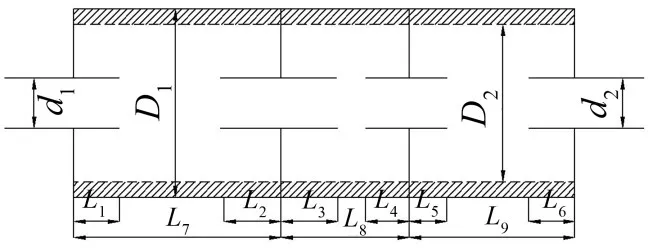
图7 阻抗复合式消声器示意图
图8为不同频率下消声器轴向剖面声压级云图。可以看出,在频率较低时,进出口管道内部声场基本上为平面波分布;当频率超过进出口管道平面波截止频率时,整个消声器内部呈现三维声场分布。

图8 轴向剖面声压级云图
在消声器进出口面上分别选取三个位置不同的观测点,提取各观测点上的声压值,结果如图9和图10所示。可以看出,在截止频率之前,进出口面上声场以平面波分布为主,各观测点处的声压值基本相同;在截止频率之后,消声器进出口面上已不再是平面波,三个位置处的声压值产生了明显差异,声压值与观测点的位置相关。
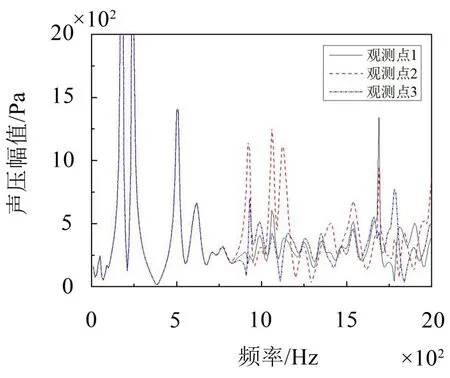
图9 进口面上声压幅值响应曲线
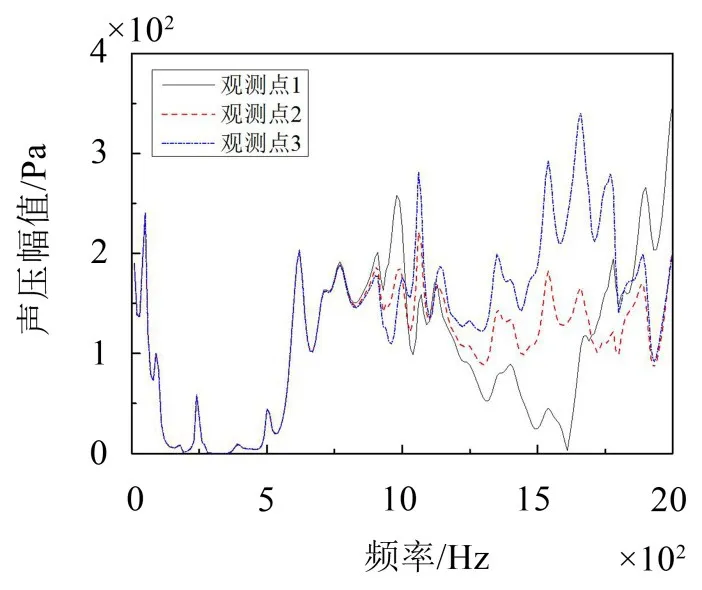
图10 出口面上声压幅值响应曲线
图11为使用三个观测点处的声压计算得到的消声器的传递损失。可以看出,三组结果在截止频率之前基本相同,在截止频率之后出现了较大偏差,而且部分频率处传递损失还出现了负值。可见,当非平面波出现时,传统方法计算消声器传递损失的结果与选取的进出口面上的观测点有较大关系,这是不合理的。
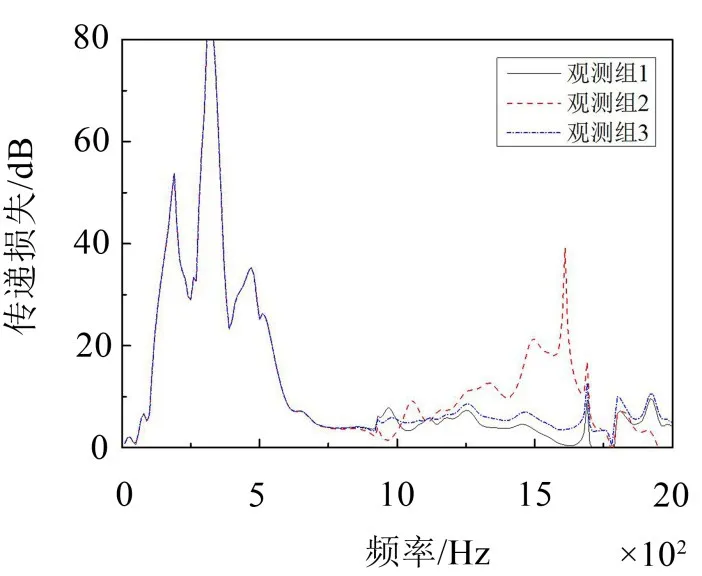
图11 消声器传递损失计算结果
为了进一步考虑进出口管内的非平面波效应,分别使用Virtual Lab Acoustics中的管道声模态法和本文的单元能量叠加法计算该消声器的传递损失,计算结果如图12所示。可以看出,两种方法计算得到的传递损失曲线在截止频率之前吻合很好,在截止频率之后的大部分频率范围内两者计算结果较为接近,在一些频率范围处存在一定的差异。
本文方法计算结果与管道声模态法计算结果出现差异的主要原因可以归纳为以下几点:
(1)本文方法在计算总声功率时,将进出口面划分为有限个单元,存在某些单元上声压变化略大,不满足平面波要求的情况;
(2)本文方法并未考虑介质的黏性效应等因素。
(3)Virtual Lab Acoustics管道声模态法所采用的AML技术模拟无反射边界的精准程度还有待考察。
本文方法的主要优势在于可以计算管道截面为任意形状的消声器的传递损失,而管道声模态法只能对进出口管道为圆形或方形的消声器进行计算。
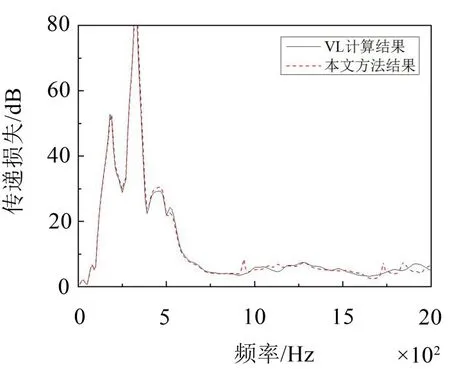
图12 阻抗复合式消声器的传递损失
3 结语
使用有限元法,建立了基于单元能量叠加法计算消声器宽频传递损失的方法,分析了进出口管道内非平面波对消声器传递损失计算结果的影响。通过使用本文方法自编程序计算结果与管道声模态法计算结果的比较,验证了本文方法的正确性。本文方法的最大优点是适用于任意形状消声器宽频传递损失计算,且能有效地考虑非平面波影响。
[1]毕嵘.复合式消声器声学特性的分析方法和实验研究[D].合肥:合肥工业大学,2012.
[2]季振林.消声器声学理论与设计[M].北京:科学出版社,2015.
[3]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.
[4]REDDY J.N.An introduction to the finite element method[M].New York:Mc Graw-Hill,2005.
[5]詹福良,徐俊伟.Virtual.Lab Acoustics声学仿真计算从入门到精通[M].西安:西北工业大学出版社,2013.
Element Energy Superposition Method for Transmission Loss Prediction of Silencers
WANG Shi-hua,JI Zhen-lin
(School of Power and Energy Engineering,Harbin Engineering University,Harbin 150001,China)
The high-order modals are excited above the plane wave truncation frequency of the silencer’s inlet and outlet pipes.Therefore,the traditional method to calculate the transmission loss of the silencer is no longer applicable since it assumes that it is the plane wave which propagates in the inlet and outlet pipes.In the present paper,by using the finite element method,the inlet and outlet sections are divided into several elements and the sound field distribution on each element is approximated as plane wave.Then,the method for calculating the transmission loss of the muffler is established based on the element energy superposition.Three kinds of silencers are chosen to calculate the transmission loss by using the present method and Virtual Lab Acoustics code,and their non-plane wave behaviors are analyzed.The results show that the present method is feasible and can effectively consider the influence of the non-plane wave.
acoustics;silencer;transmission loss;non-plane wave;finite element method;element energy superposition
O422.6
A
10.3969/j.issn.1006-1355.2017.05.039
1006-1355(2017)05-0189-04
2017-03-29
国家“863”高技术研究发展计划资助项目(2014AA041502)
王世华(1989-),男,山东省济宁市人,硕士研究生,主要从事噪声控制研究。
季振林,男,教授,博士生导师,主要从事噪声控制与消声器设计。
E-mail:jizhenlin@hrbeu.edu.cn
