BTA深孔钻杆系统流固耦合非线性动力学研究

马国红，沈兴全

（中北大学 机械与动力工程学院，太原 030051）

BTA深孔钻杆系统流固耦合非线性动力学研究

马国红，沈兴全

（中北大学 机械与动力工程学院，太原 030051）

提出一种研究深孔钻杆系统流固耦合的非线性动力响应的方法。基于输液管道的理论，考虑钻杆和切削液耦合作用来构建钻杆系统的动力学模型。采用Galerkin方法对系统运动方程进行离散，并运用四阶Runge-Kutta方法获得系统方程的数值解。通过系统的分岔图、相图和频谱图，分析了钻杆系统振动的非线性特性。研究数值结果表明，钻杆系统具有丰富复杂的非线性动力特性，如周期性运动，拟周期运动和混沌运动，能够为深孔钻杆系统动态设计及控制提供理论指导。

振动与波；深孔加工；非线性动力学特性；流固耦合；Galerkin方法

深孔加工系统是一个内部相互作用复杂的系统，在深孔加工过程中，存在着刀杆涡动、刀具颤振、切削液扰动等非线性动力学行为，然而深孔加工过程是封闭式或半封闭式切削，对这些行为无法进行观测和有效控制，从而对深孔加工系统及加工质量产生不良的影响[1–4]。

针对深孔加工过程钻杆系统的动态行为，国内外学者进行了大量的研究。胡占齐等人研究了BTA深孔加工中钻杆和工件内孔壁间楔形空间所产生的流体润滑力而引起钻杆涡动，分析了钻杆涡动和失稳的力学机理与条件[5]。孔令飞等人所建立的钻杆系统动力学模型考虑了质量偏心和非线性流体力等影响因素，采用有限元方法分析多跨柔性钻杆深孔加工系统的非线性动力学行为，此外，运用改进的打靶法研究钻杆系统的局部稳定性和分岔行为[6–8]。Thil等人采用实验手段研究切削速度和进给率对BTA深孔加工过程的影响，从切屑的形态、宽度、破碎比和压缩率等方面对钻削条件进行评价[9]。Hussien提出了一种通过在钻杆和工件之间以内部作用力的形式引入系统激励来研究BTA深孔钻杆系统涡动的方法[10]。Kenichiro建立分析颤振的模型，详细地分析了辅助支撑和油压头对钻杆振动的影响[11]。

目前，对于深孔钻杆系统动力学行为的研究，所建立的分析模型往往仅考虑对钻杆的作用力。然而，在深孔加工系统中受力情况是复杂的，并且彼此相互作用，因此需要研究深孔加工系统中的耦合效应。通过建立深孔加工系统耦合动力学模型，分析耦合动力学特性，为实际生产加工提供理论指导。本文建立钻杆系统流固耦合动力学模型，研究钻杆与切削液相互耦合作用对深孔钻杆振动特性的影响。

1 系统运动方程

在深孔加工过程中，切削液在高压的作用下流经钻杆以实现冷却、润滑以及排屑的目的，钻杆的受力情况较为复杂。本文着重研究钻杆与其内部切削液耦合动力学特性，忽略切削力、支撑作用及轴向力对钻杆振动的影响，将钻杆视为简支梁模型。基于输流管道理论，建立钻杆系统运动方程为

式中M单位长度切削液质量，m单位长度钻杆质量，U切削液流速，I为钻杆横截面惯性矩，A为钻杆横截面面积，l为钻杆长度，E杨氏模量，t为时间，a黏弹性阻尼系数，x为沿钻杆中轴线坐标。

对方程（1）进行无量纲化，为此引入如下无量纲变量

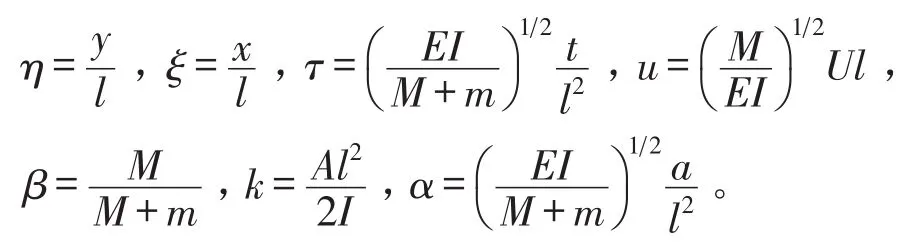
方程（1）可重新写为如下无量纲形式

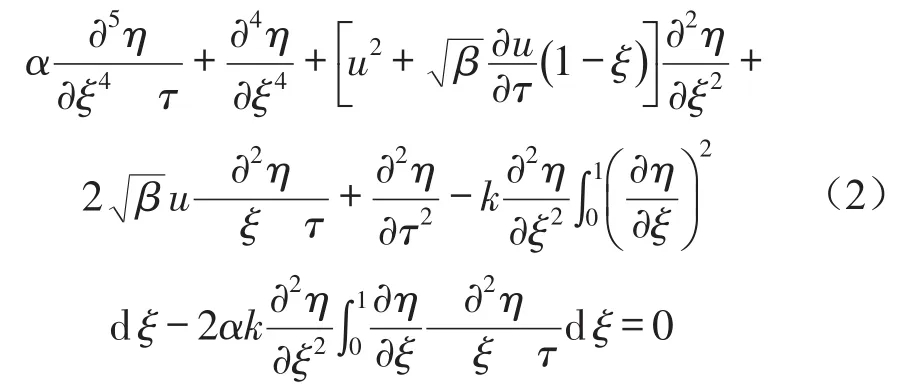
假设流速为脉动流，无量纲流速定义如下

其中u0为平均流速，μ为流速波动幅值，ω为脉动频率。

2 系统方程离散化

采用Galerkin方法将方程(2)在模态空间内展开，设

其中qi(τ)为广义时间坐标，φi(ξ)为简支梁正交模态函数，φi(ξ)的表达式为

其中：特征值λi是特征方程sinλi=0的解。

在本文研究中，取式（3）截断项数N=2，所得特征方程前2阶特征值为

将式（3）代入方程式（2），并在方程两边同时乘以φj(ξ)，然后对方程从0到1进行积分，经过化解整理可得方程为

式中

其中B0到B5的元素可分别表示为

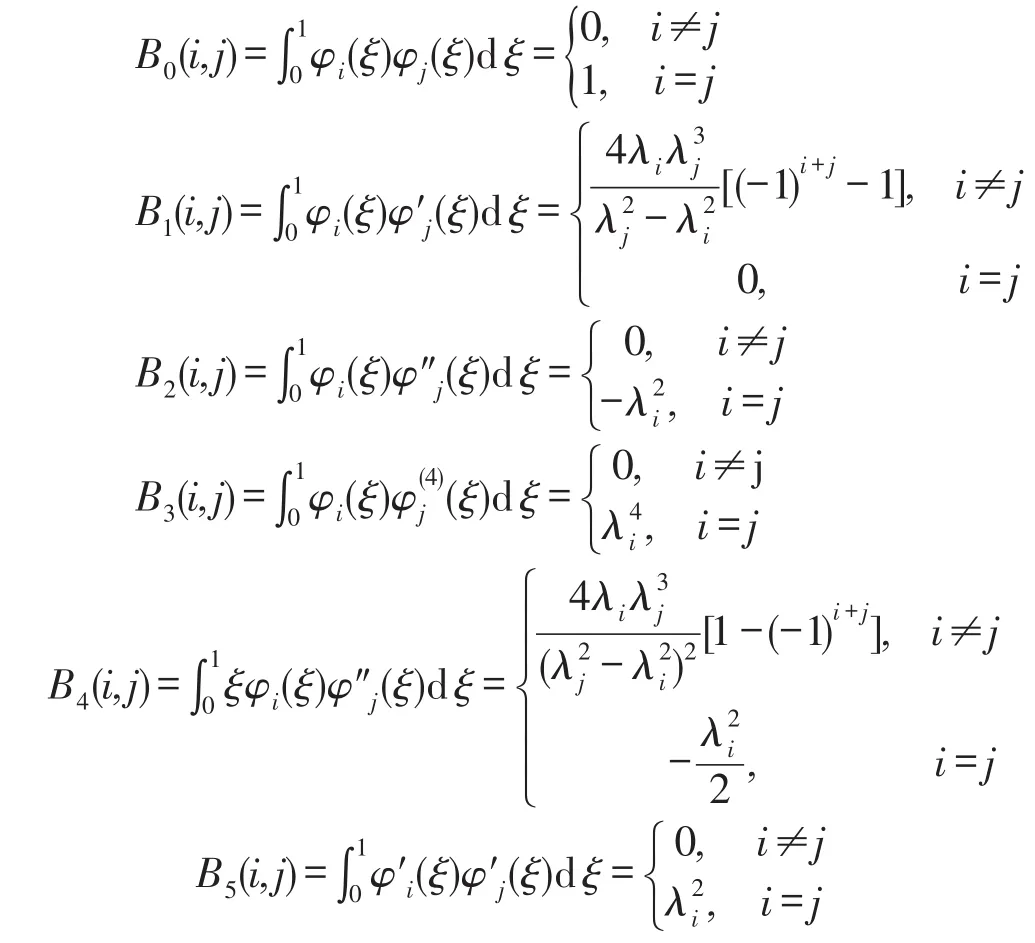
为了便于数值求解，引入状态向量

将式（6）代入方程（5），化解整理可得

式中

其中S，T以及Q可分别表示为

3 数值结果与分析

采用4阶Runge-Kutta方法对钻杆系统流固耦合动力学方程进行求解。钻杆系统参数：钻杆长度为5 m，内径为26 mm，外径30 mm，杨氏模量2.14×1011Pa，黏弹性系数取 0.000 5，钻杆密度为7.8×103kg/m3，切削液密度为 0.865×103kg/m3。本文中无量纲流速取值为3.5，脉动幅值取值为0.4。

取脉动频率作为系统分岔参数，图1为钻杆中轴线中点处振动位移随脉动频率变化的分岔图。从图1(a)中可以看出，随着脉动频率的增加，钻杆系统响应呈现出多种非线性动力学行为，包括周期运动、拟周期运动和混沌运动。

通过对比图1(a)、图1(b)和图1(c)可以看出，当1＜ω＜11.3，33.7＜ω＜36.8和47.8＜ω＜50时，在这几部分区域中，钻杆系统动力学响应主要表现为拟周期运动和混沌运动，当然其中也存在着少数的周期运动。从图1(c)可以清晰地观察到在大量的拟周期运动和混沌运动中出现少量的周期运动，比如在激励频率区间49.49＜ω＜49.63。

如图2所示为ω=10时钻杆系统混沌响应的相图和Poincare映射图。

图1 钻杆系统振动位移随激励频率变化的分岔图

图2 ω=10时钻杆系统混沌运动

图3 ω=35时钻杆系统拟周期运动

如图3所示为ω=35时钻杆系统拟周期响应的相图和Poincare映射图。然而，拟周期运动和混沌运动是难以直接从系统分岔图和相图中区分出来的，而Poincare映射图是分辨两者最为有效的手段。通过对比分析图2(b)和图3(b)的Poincare映射图，可以发现混沌运动的Poincare截面上是堆积的散点，而拟周期运动的Poincare截面上是一封闭的曲线，这是混沌运动和拟周期运动极为明显的差异。

在系统分岔图的其他区域中，钻杆系统响应主要为周期性运动，而少数的拟周期运动和混沌运动也伴随着出现，如图1(b)所示。

如图4所示为ω=21时钻杆系统响应为周期三运动的相图。

图4 ω=21时钻杆系统周期三运动的相图

如图5所示为ω=25时钻杆系统响应为周期运动的相图。

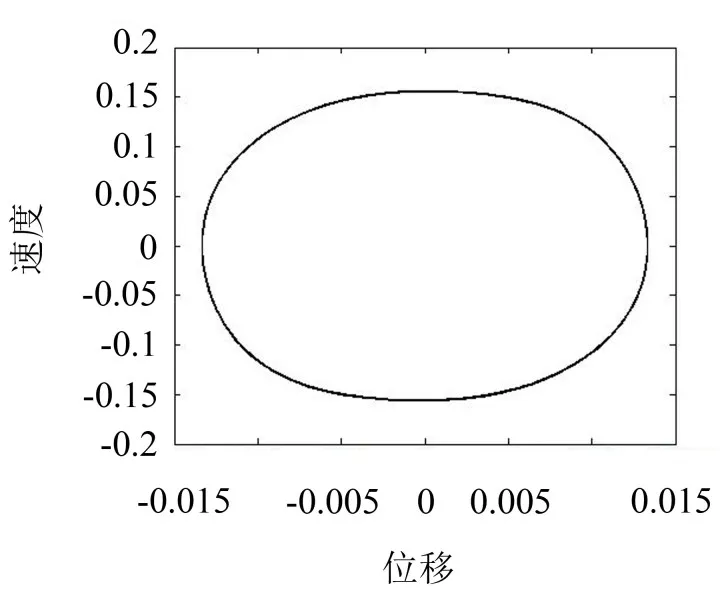
图5 ω=25时钻杆系统周期运动相图

如图6所示为ω=28.2时钻杆系统响应为周期四运动的相图。

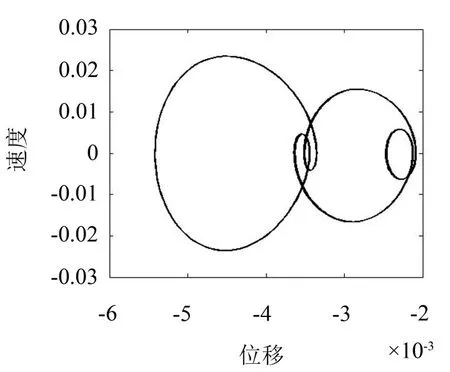
图6 ω=28.2时钻杆系统周期四运动相图

4 结语

本文建立了钻杆系统流固耦合动力学模型，对系统运动方程进行了数值求解。研究结果发现钻杆系统响应形式非常丰富，包含多种形式的周期运动、拟周期运动以及混沌运动，进一步分析了钻杆系统非线性动力学特性，为钻杆系统动态设计及控制提供理论指导。

[1]何宁.高速加工理论与应用[M].北京：科学出版社，2010.

[2]沈兴全，庞俊忠.深孔加工关键技术研究[J].中北大学学报(自然版)，2010，5(6)：43-46.

[3]何定健，李建勋，王勇.深孔加工关键技术及发展[J].航空制造技术，2008(21)：90-93.

[4]李文亮.高效深孔加工技术的研究[D].兰州：兰州理工大学，2012.

[5]胡占齐，赵武，缪磊.BTA深孔加工中流体力引起的钻杆涡动的研究[J].机械工程学报，2005，41(1)：230-233.

[6]KONG LINGFEI,LI YAN,ZHAO ZHIYUAN.Numerical investigating nonlinear dynamic responses to rotating deep-hole drilling shaft with multi-span intermediate supports[J].InternationalJournalofNon-Linear Mechanics,2013,55:170-179.

[7]KONG LING FEI,LI YAN,LU YAN JUN,et al.Complex nonlinear behaviors of drilling shaft system in boring and trepanning association deep hole drilling[J].International Journal of Advanced Manufacturing Technology,2009,45:211-218.

[8]LINFEI KONG,YAN LI,YANJUN LV,et al.Numerical investigation on dynamic characteristics of drilling shaft in deep hole drilling influenced by minimal quantity lubrication[J].Nonlinear Dynamics,2013,74(4):943-955.

[9]THIL J,HADDAG B,NOUARI M.Experimental and analytical analyses of the cutting process in the deep hole drilling with BTA system[J].Mechanics and Industry,2013,14(6):413-429.

[10]HUSSIEN M AL-WEDYAN,RAMA B BHAT,et al.Whirling vibrations in boring trepanning association deep holeboring process[J].JournalofManufacturing Science and Engineering Transactions of the ASME,2007,129(1):48-62.

[11]KENICHIRO MATSUZAKI,TAKAHIRO RYU,ATSUO SUEOKA,et al.Theoretical and experimental study on rifling mark generating phenomena in BTA deep hole drilling process[J].International Journal of Machine Tools&Manufacture,2015,88:194-205.

Study on Nonlinear Dynamic Responses of a BTADeep-hole Drilling Shaft System with Fluid-structure Interaction

MA Guo-hong,SHEN Xing-quan
(School of Mechanical and Power Engineering,North University of China,Taiyuan 030051,China)

An approach to analyze the nonlinear dynamic responses of the deep-hole drilling shaft system considering fluid-structure interaction is presented.Based on the theories of fluid flow in pipelines,the governing dynamic equations of the drilling shaft system are constructed considering the interaction between the drilling shaft and the cutting fluid.The dynamic equations are discretized using Galerkin method.The fourth order Runge-Kutta method is used to obtain the numerical solution of the equations.The nonlinear characteristics of the drilling shaft system are further analyzed by the bifurcation diagram,phase diagram and spectrogram of the dynamic system.The numerical results in this study show that the drilling shaft system has rich and complex nonlinear dynamic behaviors such as periodical motion,quasi-periodical motion and chaotic motion.This work may provide a theoretical guidance for dynamic design and control for deep hole drilling systems.

vibration and wave;deep hole drilling;nonlinear dynamic behavior;fluid-structure interaction;Galerkin method

TH113

A

10.3969/j.issn.1006-1355.2017.05.008

1006-1355(2017)05-0038-04

2017-02-27

国家国际科技合作资助项目(2013 DFA70770)；高等学校博士学科点专项科研基金资助项目(20131420110002)；中北大学研究生科技立项项目(20161312)

马国红（1987－），男，山西省朔州市人，博士生，主要研究方向为深孔加工非线性动力学研究。

E-mail:mgh266088@163.com