MARG传感器误差分析与标定方法研究∗

梁益丰 许 微 曹 勇

（海军工程大学导航工程系 武汉 430033）

MARG传感器误差分析与标定方法研究∗

梁益丰 许 微 曹 勇

（海军工程大学导航工程系 武汉 430033）

MARG传感器成本低廉、导航参数全面，在工程领域应用广泛，但存在精度低，误差大的问题。针对此问题，利用三轴惯性转台对某型MARG传感器的三部分完成标定。首先分别分析了MARG三部分传感器的误差特性，然后引入适合各传感器的输出模型和标定方法；其次，对采集的数据进行处理，得到各传感器的误差参数；最后补偿误差，验证了加速度计六位置法、陀螺仪角速率标定和磁传感器八位置法标定的有效性，为该MARG传感器的实际应用提供了依据。实验结果表明，基于三轴惯性转台的几种标定方法的精度能够满足一般应用的需求，但也存在改进空间。

三轴惯性转台；MARG传感器；误差标定与补偿

C lassNum ber TP212

1 引言

目前，MIMU（加速度计和陀螺仪）和磁传感器（三类合称MARG）因价格低廉、使用方便而广泛应用于微小型无人机、机器人和室内定位等领域［1］，但是误差较大，因此需要对其性能参数进行测试和标定，以提高精度。现探究在三轴转台载体上，用几种常规方法对某型MARG传感器标定的精度，总结其标定效果与存在不足。

2 三轴加速度计标定

2.1 加速度计误差分析和标定模型

三轴加速度计的标定误差大致分为以下几类：仪器仪表类型误差、温度误差、随机误差等。温度相对稳定情况下，仪器仪表类型误差为主要误差源，且由于MARG传感器主要应用于中低精度测量，可忽略较小的二次非正交误差项。由此建立数学误差模型如下［2～4］：

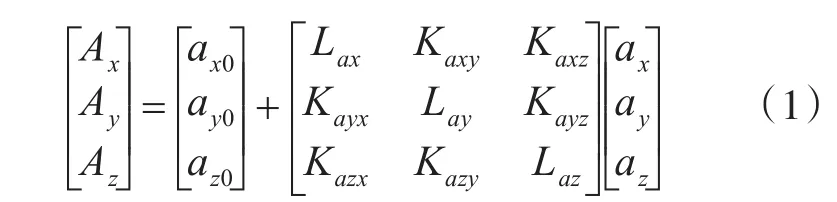
其中，Ax、Ay、Az为输出值；ax0、ay0、az0为零位输出；ax、ay、az为各轴敏感到的真实加速度；Lax、Lay、Laz为刻度因数；敏感轴ax存在两个安装误差系数Kaxy、Kaxz，对应安装误差角θxy，θxz；同理，敏感轴ay和az分别存在两个安装误差系数，对应两个安装误差角。

由误差模型即式（1）可推导其误差补偿模型，可表示为

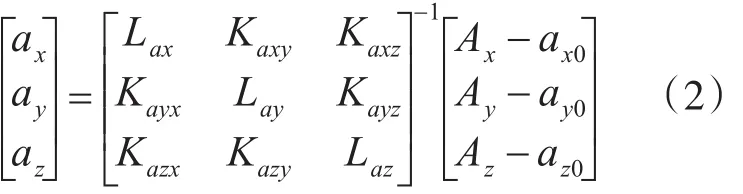
2.2 三轴加速度计的6位置标定

基于三轴转台提供的高精度姿态角作为参考基准，采取六位置法［5～7］对加速度计进行标定。实验具体步骤如下：1）将MARG传感器各轴与三轴惯性转台各轴对齐安装，并加以固定；2）调整转台位置，使传感器依次处于如表1所示的六个位置；3）在转台静止状态下，在各位置采集多组加速度计部分输出的平均值作为该位置的输出值。每组数据采集时间为10s，采样频率为10Hz。

表1 加速度计所处的六个位置及各轴重力加速度

X轴在各位置的输出值分别依次表示为：Ax1、Ax2、Ax3、Ax4、Ax5、Ax6，Y、Z轴类似。经六位置方程联立，可得X轴各参数的解如式（3）所示：

同理可得到Y轴与Z轴各参数相似形式的解。

采集MARG加速度计部分的输出值，综合以上方程式可求得各误差参数如表2所示。

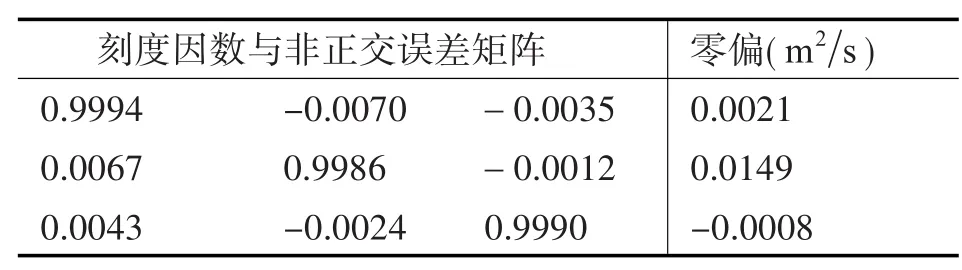
表2 加速度计误差参数

经换算，加速度计的误差补偿模型为

2.3 六位置法标定效果验证

观察所测数据，位置1、位置4的输出值与标准值有较大偏差，其余四个位置的输出值精度基本满足要求。因此以位置1和位置4为例，比较补偿前后的数据与理论值之差。

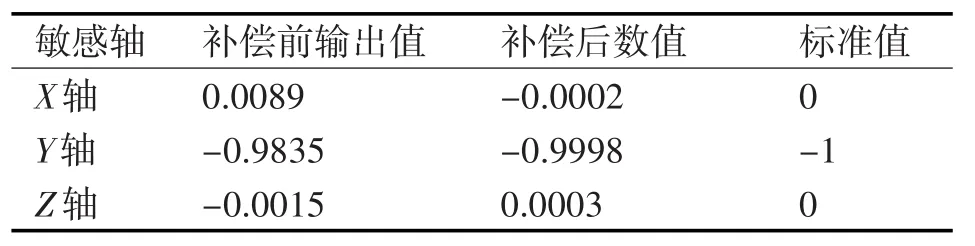
表3 位置1标定补偿前后结果对比

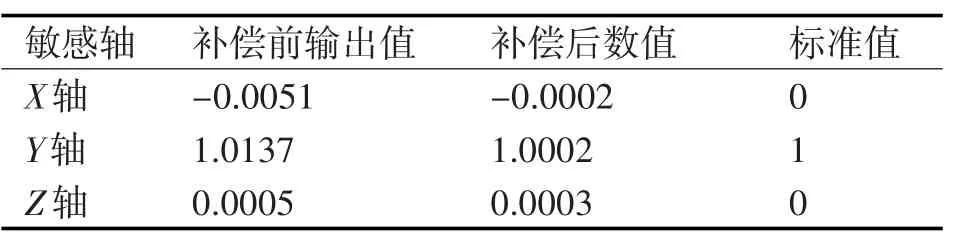
表4 位置4标定补偿前后结果对比

可以看到，补偿后三轴加速度计测量值与对应理想值的误差变小补偿后误差普遍降低了1～2个数量级，与理论值之差达到万分级，说明六位置标定方法可行，所建立的数学模型准确可靠。但六位置法求解过程中，并没有首先剔除安装误差，位置间不存在相互补偿关系，因此所求零偏包含了真实零偏和安装误差两部分。可以通过自转轴指北等方法［8］求解安装误差，得到精确的零偏值。

3 三轴陀螺仪标定

3.1 陀螺仪误差分析与建模

陀螺仪主要误差源按其性质可分为元件误差、安装误差、初始值误差、干扰误差等。按照实验要求，陀螺仪X、Y、Z三个敏感轴应相互严格垂直，用于精确跟踪各个轴向的角运动。实际使用时，安装误差角是造成陀螺仪测量误差的主要原因。此外，噪声等干扰对标定结果影响较小且是一个随机小量，在标定时可忽略。由此建立陀螺仪误差模型［9～10］：

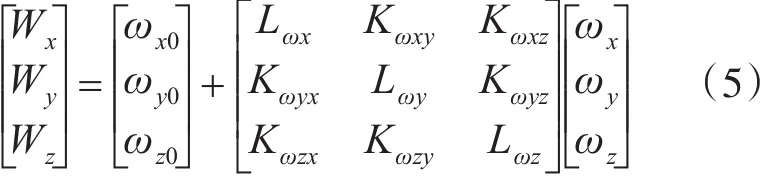
式（5）中Wx、Wy、Wz为实际输出值；ωx0、ωy0、ωz0为零位输出；ωx、ωy、ωz为各轴敏感到载体真实运动的角速率；Lωx、Lωy、Lωz为刻度因数；Kωxy、Kωxy、Kωyx、Kωyz、Kωzx、Kωzy为安装误差角所致的三轴陀螺仪的6个非正交误差系数。

3.2 陀螺仪的角速率标定方法

将MARG传感器通过夹具固定安装在三轴转台上，标定轴与转台转轴平行。给转台一个固定的速率值，测量陀螺仪部分输出的位置和速度信息。转台速率值的取法按照GB-321规定的R5系列选取［11］。

按标准取转台角速率值±25，±40，±63（单位：°/s），标定步骤如下［12～14］：

1）接通三轴惯性转台的电源，根据实验具体要求进行半小时预热；

2）设置转台为速率模式，按照三轴六速率共18种模式的各个不同角速率驱动转台；

3）设置采样时间为100s，频率10Hz，取陀螺仪输出均值作为该角速率值下的输出值。

由式（5），陀螺仪零偏ωx0、ωx0、ωz0可以表示为

Wx+、Wy+、Wz+为转台各速率模式下旋转轴正转时的测量值；Wx-、Wy-、Wz-为转台各速率模式下旋转轴反转时的测量值，将求取的各轴零偏平均值作为陀螺仪零偏。

将实验采集的陀螺仪实际输出值代入式（5）数学模型，由最小二乘法可得刻度因数和非正交误差系数。求得12个误差参数如表5所示。

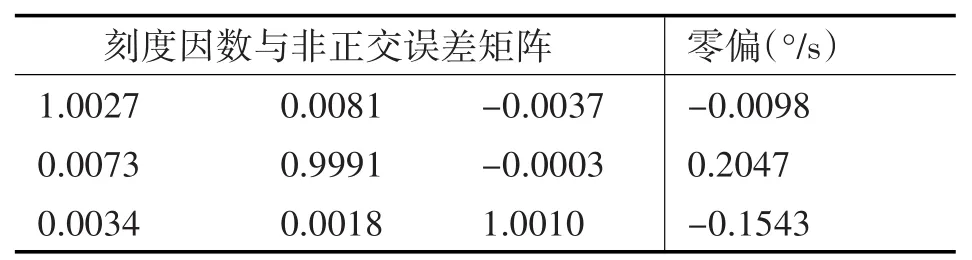
表5 陀螺仪误差参数

经变换可以得到陀螺仪标定补偿后的表达式，如式（7）所示：

以模式5、11、17所测陀螺仪数据为例，分析该标定方法的有效性，标定补偿前后陀螺仪的数据对比曲线如图1～图3所示。

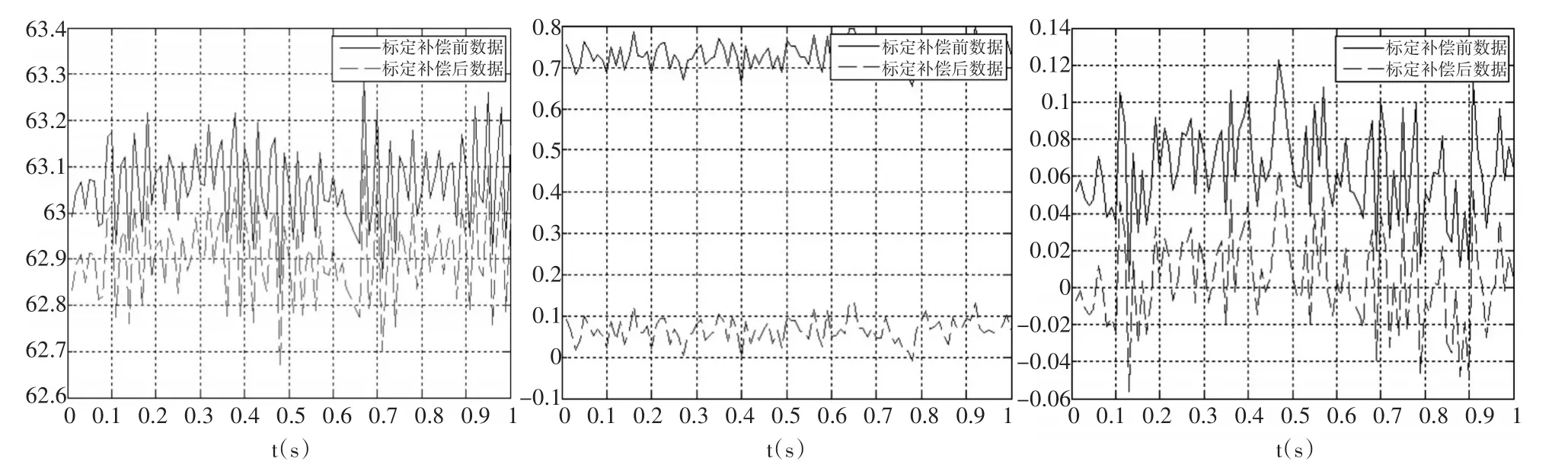
图1 模式5陀螺仪数据对比

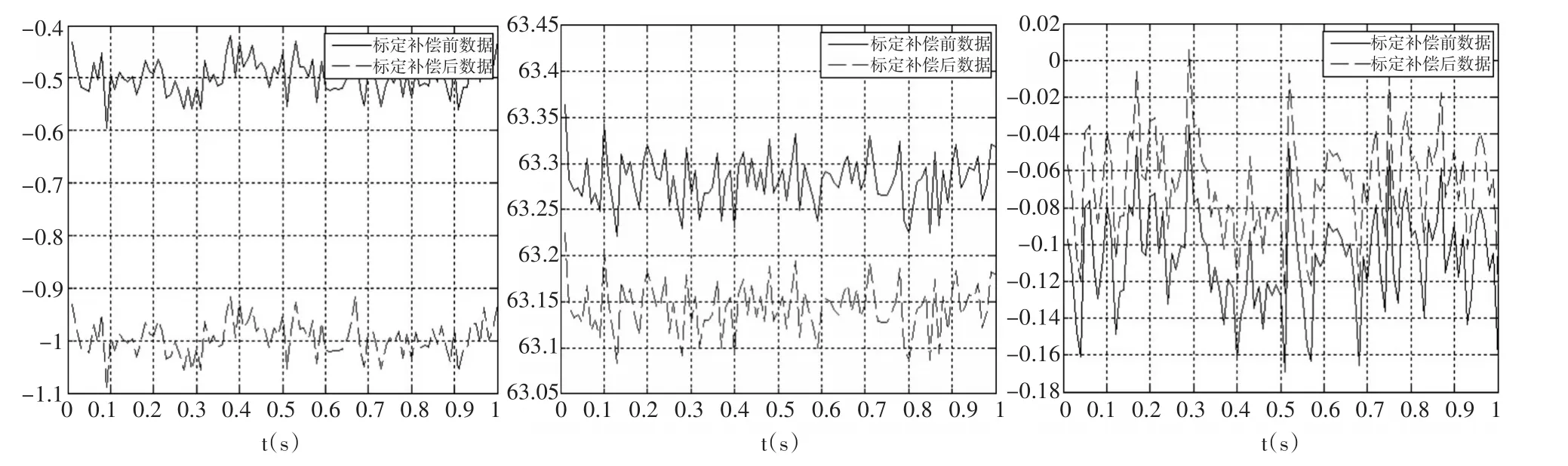
图2 模式11陀螺仪数据对比

图3 模式17陀螺仪数据对比

图1 ～图3中从左至右分别为陀螺仪X、Y、Z轴数据对比曲线，其中蓝色和红色曲线分别为标定补偿前后陀螺仪数据。总体来讲，对Y、Z轴的标定效果良好，X轴标定前后误差变化不大，甚至略有增加，这可能是因为Y轴自身误差较大引起的。说明在某一轴安装误差较明显时，角速率标定有一定的局限性，即：要求三个轴的精确度相对接近。可以通过提高安装标准、利用卡尔曼滤波精简数据等方式减小这种局限。同时，陀螺仪每组转速之间抵消了安装误差，零偏较为准确。

4 磁传感器标定

4.1 磁传感器误差分析与模型建立

磁传感器有以下误差［15］：

1）标度因数误差：因生产水平所限造成的偏差，为仪器固有误差。包括正交误差、零偏等。

2）安装误差：传感器普遍存在的误差，因三个轴未能严格安装而产生失准角。

3）罗差：即使处于磁场干净的环境，仍然存在铁质引起的磁强度变化，称为罗差［16］。

其中，正交误差项与失准角误差项，都可归类为磁传感器三个敏感轴不水平正交而产生的误差；零偏包含安装固有零偏和安装误差引起的小量。总体来讲，可以将磁传感器的误差分为非水平正交引起的误差项和零偏。由此建立误差模型方程如式（8）所示：

将误差方程式展开可得

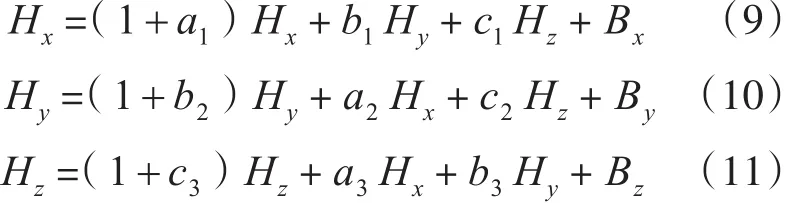
矩阵A代表非正交误差矩阵，分别对应三个轴的标度因数误差，矩阵B代表磁传感器的零偏。根据误差来源分析，所建立方程合理。

4.2 八位置系统误差标定

八位置系统误差标定方法是将MARG固定于三轴转台，调整转台的姿态到八个特定角度，经过解算求出磁传感器系统误差模型系数矩阵A和矩阵B，对系统误差进行补偿。八个特定位置详见表6。

表6 八位置试验次序

磁传感器的零位偏差可由式（12）求出：

将矩阵A写成式（13）的形式：

通过位置2，4，5，7，联立方程如式（14）和式（15），二者相减即得到关于a的方程，见式（16），矩阵a中包含a1，a2，a3三个参数。

同理，选取恰当的四个位置可以求解b、c。Hu和Hn分别为当地天向磁场和北向磁场的理论值［17］，引入Hu和Hn值即可求出 a，b，c的具体值。代入模型，实现系统误差补偿。

4.3 模型求解

将磁传感器固定在三轴转台上，清理现场可能引起磁场变化的铁质等。按照表6给的8个位置调整转台姿态，采集数据，解算出误差系数矩阵A和B，见表7和表8。

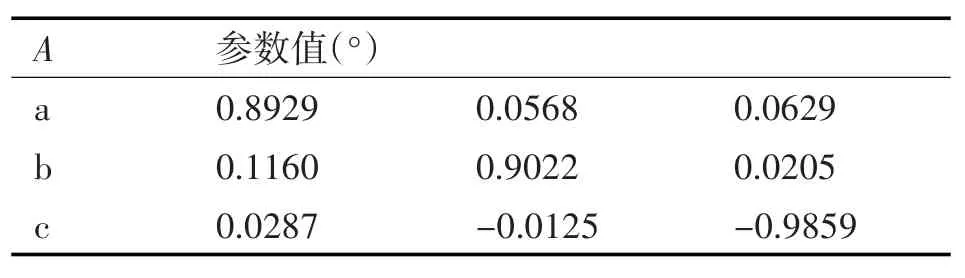
表7 磁传感器参数标定结果（矩阵A）

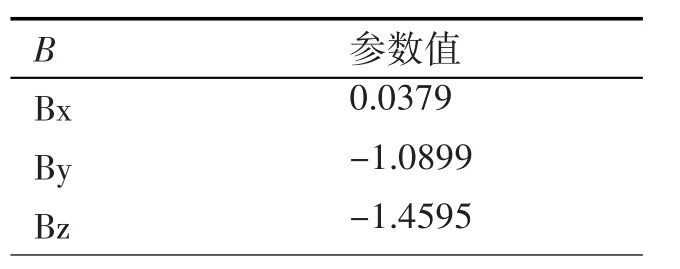
表8 磁传感器参数标定结果（矩阵B）

验证结果表明，用三轴转台八位置翻转法标定磁传感器误差大，经补偿有一定效果。但实验条件要求多，考虑到实验室与传感器实际应用场所磁强度不一，难以直接投入使用。综合来看，磁传感器应在使用环境中利用椭球拟合标定为宜［18～20］。

5 结语

利用三轴转台完成了MARG三部分传感器的误差标定。采取恰当方法，求解出各部分传感器的标度因子，使传感器可以投入实际使用。分析补偿前后误差的变化，验证了几种常用标定方法的有效性。总结了相应方法的局限性并提出改进手段，为不同条件下进行、对精度有不同要求的试验提供了依据。

［1］沃克尔·肯普.惯性MEMS器件原理与实践［M］.北京：国防工业出版社，2016：298-300.

［2］宋丽君，秦永元.MEMS加速度计的六位置测试法［J］.测控技术，2009，28（7）：12.

［3］Wang Mei，Wang Yongquan，Zhang Yanhua.Adaptive filiter foraminiature MEMSbased attitude and heading reference system［J］.Journal of Harbin Institute of Technology（New Series），2006，13（5）：27.

［4］Bian Chao，Xu Yuanyuan，Sun Hongguang.Amicro amperometric immunosensor based on MEMS［J］.Jounral of Electronics&Information Technology， 2006，（11） 4：11-15.

［5］石玺文，李杰，胡陈君，秦丽.MEMS三轴加速度计6位置标定方法的研究［J］.电子器件，2016，39（2）：404.

［6］Peng X，Zhang T，Li J，et al.Field Calibration of Three-AxisMEMSDigital Acceleration［J］.Journalof Vibration，Measure-mentand Diagnosis，2014，34（3）：544-548.

［7］杨常松，徐晓苏.捷联惯导系统加速度计标度因数和安装误差的试验标定［J］.测控技术，2005，24（12）：57-59.

［8］赵桂玲.光学陀螺捷联惯性导航系统标定技术［M］.测绘出版社，2014：40-42.

［9］宋丽君，秦永元.MEMS陀螺仪的一种实用标定法［J］.压电与声光，2010，32（3）：373.

［10］ZHAO Zhijin ，ZHOU Yunshui，SHANG Junna.Modulation recognition based on the time frequency analysis and RBFneuralnetwork［J］.Piezoelectrics&Acoustoo ptics，2004，26（4）：328-330.

［11］柳征，姜文利，周一宇.基于小波包变换的辐射源信号识别［J］.信号处理，2005，21（5）：460-463.

［12］KENICHINishiguchi，MASAAKIKobaya shi.Improved algo rithm fo restimating pulse repetition intervals［J］.IEEETranson AES，2000，36（2）：407-421.

［13］彭孝东，陈瑜，李继宇，闫国琦，张铁民.MEMS三轴数字陀螺仪标定方法研究［J］.传感器与微系统，2013，32（6）：64.

［14］林恒，魏莹莹，李保国.一种八位置数字磁强计系统误差标定方法［J］.传感器与微系统，2011，30（3）：88.

［15］袁智荣.三轴磁航向传感器的全姿态误差补偿［J］.传感器技术，2003，22（9）：35.

［16］王璐.组合式航向系统关键技术研究［D］.西安：西北工业大学，2007：35.

［17］赵希亮，边刚，金绍华，王美娜，刘强.世界地磁场模型WMM2015 误差分析与评估［J］.海洋测绘，2016，36（3）：12-13.

［18］张樨，李杰，蒋窍，张晓明.基于椭球拟合的三轴磁传感器快速标定补偿方法［J］.机械工程与自动化，2012，4：164-165.

［19］杨晓东，王炜.地磁导航原理［M］.北京：国防工业出版社，2009：90.

［20］袁智荣.磁航向传感器使用中的误差补偿［J］.测控技术，2001，20（1）：58-59.

Research on Error Analysisand Calibration Method ofMARG Sensor

LIANG Yifeng XUWei CAO Yong
（Departmentof Navigation，Naval University of Engineering，Wuhan 430033）

MARG sensor is low cost，comprehensive navigation parameter，widely used in engineering field，but there are problems of low precision and large error.To solve this problem，three-axis inertial turntable is used to calibrate the three parts ofa MARG sensor.Firstly，the error characteristics of the MARG three-partsensor are analyzed respectively，and then the outputmodel and calibration method suitable for each sensor are introduced.Secondly，the experimental data is collected，screened and processed seriously.Finally，the compensation error is used to verify the accuracy of the six-position accelerometer six-positionmethod，the gyro angular rate calibration and themagnetic sensoreight-positionmethod，which provides the basis for the practicalapplication of the MARG sensor.The experimental results show that several commonly used calibrationmethods based on the three-axis inertialplatform have high accuracy，meanwhile，but there is room for improvement.

three-axis turntable，MARG，error calibration and compensation

TP212

10.3969/j.issn.1672-9730.2017.09.009

2017年3月11日，

2017年4月28日

梁益丰，男，研究方向：惯性技术及其应用。许微，女，讲师，研究方向：室内定位技术。曹勇，男，研究方向：信息技术。