基于改进等效旋转矢量的姿态更新算法研究∗

张昀申 曹 彪

（1.92941部队 葫芦岛 125001）

（2.海军航空工程学院 烟台 264001）

基于改进等效旋转矢量的姿态更新算法研究∗

张昀申1曹 彪2

（1.92941部队 葫芦岛 125001）

（2.海军航空工程学院 烟台 264001）

姿态更新算法是捷联惯导系统解算的核心，论文研究了姿态更新的等效旋转矢量算法，该算法在短时间内有很高的定位精度，但随着时间的延长会产生误差积累。通过改进算法可以有效降低误差，提升捷联惯导系统性能。

捷联惯导；姿态更新；等效旋转矢量；组合导航

ClassNum ber TN967.2

1 引言

姿态更新算法是捷联惯导系统解算的核心，也是影响捷联惯导系统精度的主要因素之一［1］，主要有欧拉角法、方向余弦法、四元数法、等效旋转矢量法等。Miller R B［2］提出了三子样优化算法，大大改进了锥运动环境中算法的性能。Lee JG［3］等提出四子样算法，在高频锥运动中的性能优于三子样算法。Yeon F J［4］提出了改进的捷联惯导姿态更新算法，该方法的估计误差至少减少两个数量级，同时降低了计算量。Savage PG［5～6］给出了现今捷联惯导系统中所使用的综合设计方法。Limanovich Y A［7］提出了与Savage PG给出的速度和位置算法不同的两种捷联导航算法。

四元数法和等效旋转矢量法为目前常用的姿态更新算法。但四元数算法对有限转动引起的不可交换误差的补偿程度不够，所以只适用于低动态运载体的姿态解算。对于高动态运载体，四元数姿态解算中的算法漂移十分严重。等效旋转矢量算法可以采用多子样算法来实现对不可交换误差的有效补偿，并且可通过对系数的优化处理使算法漂移在相同子样算法中达到最小，因而特别适用于用于飞机等高动态、大机动载体的姿态更新。

2 等效旋转矢量算法

由文献［1］推导的旋转矢量与姿态四元数的关系，可得：

式（1）中，⊗表示四元数乘法运算。

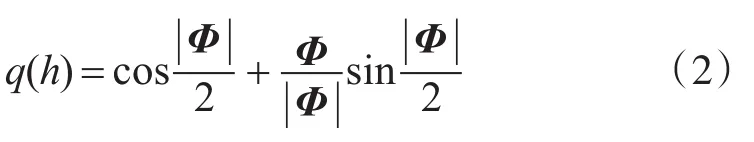
Φ为等效旋转矢量，| Φ |为Φ的模；q(h)称为[tk， tk+1]时间段内的姿态变化四元数。工程上常用

表1 航向角ψ的真值表

表2 横滚角γ的真值表

3 仿真分析

对所应用的捷联惯导算法进行Matlab仿真分析，为组合导航系统捷联惯导模块的有效性奠定基础。对于运动的载体，由于导航系统是时变的，系统矩阵和量测矩阵的确定都与载体的位置、速度有关，因而在仿真前，要对飞行轨迹进行设计，以提供仿真量测值［12］。飞机初始位置为北纬22°，东经110°，高度2000。初始航向0°，速度300m/s。对上述飞行轨迹采用原有旋转矢量算法进行仿真分析，姿态误差曲线如图1所示。

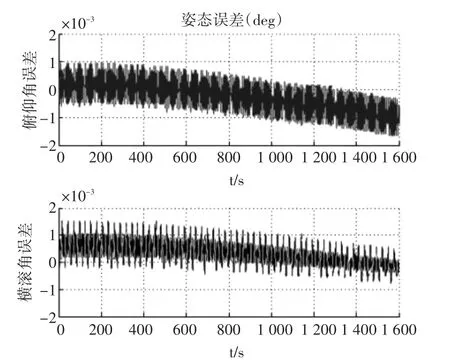
图1 姿态误差曲线

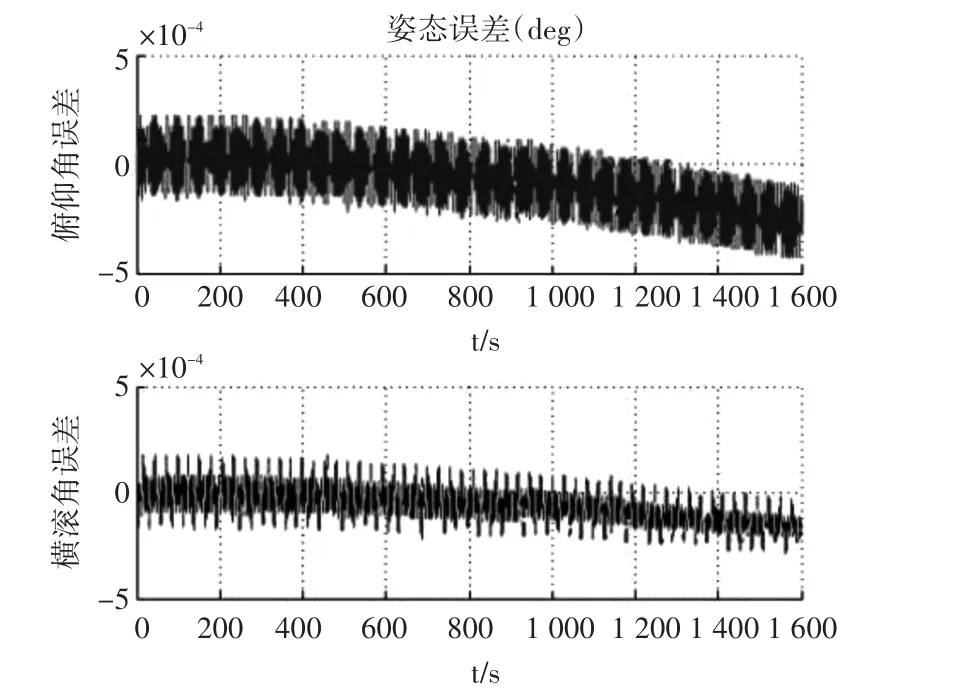
图2 算法改进后的姿态误差曲线

通过比较不难发现，改进的旋转矢量算法可以有效降低误差，提高姿态解算精度。

4 结语

本文分析了惯导姿态更新的几种算法，针对四元数算法对有限转动引起的不可交换误差的补偿程度不够，应用等效旋转矢量算法对捷联惯导姿态进行更新。仿真实验表明该算法在短时间内有很高的定位精度，但随着时间的延长，产生误差积累，通过改进算法可以有效降低误差，提升捷联惯导系统性能。

［1］秦永元.惯性导航［M］.北京：科学出版社，2006：287-287， 298-299， 306-311， 311-315， 331-333，33136，340-341，346-350.

［2］Miller R B.Anew strapdown attitude algorithm［J］.AIAAJournal of Guidance，Control and Dynamics，1983 ：6（4）：287-291.

［3］Lee JG，Yoon Y J，Mark JG，Tazartes D A.Extension of strapdown attitude algorithm for high-frequency basemotion［J］.JournalofGuidance，1990：13（4）：738-743.

［4］Yeon F J，Yu P L.Improved strapdown coning algorithm［J］.IEEE Transactions on Aerospace and Electronic Systems，1992：28（2）：48290.

［5］Savage PG strapdown inertial navigation integration algorithm design，Part 1［J］.AIAAJournal of Guidance，Controland Dynamics，1998：21（1）：19-28

［6］Savage PG strapdown inertial navigation integration algorithm design，Part 2：Velocity and Position algorithm［J］.AIAAJournal of Guidance，Control and Dynamics，1998：21（1）：208-221.

［7］Litmanovich Y A，Lesyuchevsky V M，Gusinky V Z.Two new classes of strapdown navigation algorithms［J］.AIAAJournalofGuidance，Controland Dynamics，2000：23（1）：324.

［8］ Roscoe K M.Equivalency between strapdown inertial navigation coning and sculling integrals/algorithms［J］.J.Guid.Contr.Dyn，2001，24（2）：145-1.

［9］杜继永，张凤鸣，李建文，等.高动态环境下SINS姿态更新的改进等效旋转矢量算法［J］.空间科学学报，201333（1）：85-91.

［10］戴邵武，徐胜红，史贤俊等.惯性技术与组合导航［M］.北京：兵器工业出版社，2009，204-213，120-125.

［11］张昀申.基于姿态更新算法的仿真实体行为建模［J］.计算机与数字工程，2016：44（7）：1238-1241.

［12］黄昆，杨功流，刘玉峰.舰载姿态加角速度匹配传递对准方法研究［J］.中国惯性技术学报，2006：14（1）：17-26.

Strapdown Algorithm Research Based on Im proved Equivalent Rotation Vector

ZHANG Yunshen1CAO Biao2
（1.No.92941 Troopsof PLA，Huludao 125001）（2.Naval Aeronautical Engineering Institute，Yantai 264001）

The strapdown algorithm is the key of SINS system solution，this paper researches on the algorithm of equivalent rotation vector，the algorithm has high location precision in the shortsimulation time，while there is error accumulation in the long simulation time.The error can be reduced and SINSperformance can be advanced by the improved algorithm.

SINS，strapdown，equivalent rotation vector，integrated navigation

TN967.2

10.3969/j.issn.1672-9730.2017.09.006

2017年3月8日，

2017年4月22日

张昀申，男，硕士，工程师，研究方向：组合导航。曹彪，男，硕士，讲师，研究方向：系统分析与集成。