多维数据K-means谱聚类算法改进研究
2017-10-23谢志明
谢志明,王 鹏,黄 焱
(1.汕尾职业技术学院 信息工程系,广东 汕尾 516600;2.汕尾市创新工业设计研究院 云计算与数据中心工程设计研究所,广东 汕尾 516600;3.西南民族大学 计算机科学与技术学院,四川 成都 610041;4.淮阴师范学院 计算机科学与技术学院,江苏 淮安 223300)
多维数据K-means谱聚类算法改进研究
谢志明1,2,王 鹏3,黄 焱4
(1.汕尾职业技术学院 信息工程系,广东 汕尾 516600;2.汕尾市创新工业设计研究院 云计算与数据中心工程设计研究所,广东 汕尾 516600;3.西南民族大学 计算机科学与技术学院,四川 成都 610041;4.淮阴师范学院 计算机科学与技术学院,江苏 淮安 223300)
针对传统K-means算法不能自动确定初始聚类数目k和谱聚类算法对参数敏感的问题,提出了一种基于谱聚类的K-means(PK-means)算法。该算法在对k值选取时进行了创新改进,将计算所得的高密度数据点按规律排序,选择密度点前96%的进行聚类,可以以较高的准确率取得聚类数目k,同时采用了不受参数影响且稳定性更高的基于谱聚类模糊的相似性度量方法,利用FCM算法求隶属度矩阵确定数据点间的相似性。应用PK-means算法、K均值算法与密度敏感的谱聚类算法(DSSC)进行了多维非线性数据处理的测试实验。实验结果表明,无论是对于低维数据集还是高维数据集,K-means算法的处理效率是最低的,DSSC算法稍好,而PK-means算法优势明显,其相比传统聚类算法具有更高的聚类精度和更强的鲁棒性,且维数越高,聚类性能表现越突出。
K-means算法;谱聚类算法;聚类;FCM算法;隶属度矩阵
0 引 言
聚类(Clustering)是一种将类似的对象通过物理或抽象对象集合的方式划分成若干个簇或类的过程。聚类的对象无类别标识,属于无监督学习模式,特征是使簇内的对象相似度尽可能小,簇间的对象相似度尽可能大[1-2]。聚类算法自提出以来就已成为数据挖掘领域方面一直研究的课题,伴随着云计算、大数据技术的相继问世,对聚类算法的研究更是方兴未艾,目前研究较多的聚类算法主要有基于划分的K-means、基于分层的CURE、基于网格的STRING、基于密度的DBSCANE和基于模型的SOM等方法[3-4]。
K-means算法是数据挖掘领域中应用最广泛的一种聚类分析方法,因简单、高效、收敛快和线性时间复杂度优势而被广泛应用,并被用于大数据分析,其突出特点是局部搜索能力强[5-6]。但是该算法也有明显的缺点,主要表现在初始聚类中心对聚类结果影响很大,易使算法过早陷入局部最优解;其次聚类数目k难以确定,迭代次数的增加加大了系统I/O的输出和资源的消耗,总耗时增加;第三是孤立点对算法的影响也很大,会导致聚类结果不确定,鲁棒性不高[7]。
针对该算法存在的诸多不足,已有专家学者进行了一系列的改进方案。文献[8]利用不同聚类结果子簇之间的交集构造出关于子簇的加权连通图,并通过其连通性合并子簇,使聚类结果在精度和效率上有了一定的提高。文献[9]提出了依据密度点分布的情况,将高密度分布的点定为初始聚类中心,该算法比随机选取初始聚类中心准确率高了许多,但由于选取的多个聚类中心有可能距离较为接近,失去代表性。文献[10]提出了当最大密度参数值不唯一时,最大密度参数选取的合理方案,该方案不仅提高了聚类精度,还有效避开了对孤立点的选取。文献[11]提出了以数据对象邻域为基础,选择位于数据集样本密集区且相距较远的数据对象作为初始聚类中心,该算法对噪声数据具有较强的抗干扰能力。文献[12]基于距离最远的样本点最不可能分到同一个簇中的事实,构造了一种将文本相似度转换为文本距离的方法,该方法能有效降低聚类耗时,提高F度量值。文献[13]利用数据对象的分布密度以及计算最近两点的垂直中点方法来确定k个初始聚类中心,该算法在低维数据集下有较高的准确率和稳定性,聚类高维数据集时准确率不高。文献[14]利用直方图将数据样本空间进行了最优划分,依据样本分布特点确定初始聚类中心,这种算法减少了对参数的依赖,其聚类结果的准确率和效率都有了明显提高;若针对的是高维或超高维样本数据,伴随迭代次数的增加,运算过程将趋于复杂化,从而导致算法效率下降。
改进K-means算法的方法很多,既能高效处理多维非线性数据又能自动确定聚类数k的改良方法和研究则很少。为此,利用K-means算法在低维样本空间收敛速度快、扩展性好等优点,结合谱聚类算法在高维样本空间能高效聚类任何形状类型的数据集且对维数不敏感,可避免因维数所引起奇异性问题的优势,提出了一种基于谱聚类的多维数据K-means聚类改进算法。其可将基于局部识别方法的谱聚类算法拓展至可全域收敛求最优解[15],因此适用于多维非线性数据的聚类。
1 聚类数k值的确定
K-means算法和谱聚类算法都不能自动获取到聚类数目,为解决这一问题,提出依据高密度数据点分布情况来实现聚类数目的自动确定。一般来说,数据集在低维空间中会呈现特定的分布且类类之间是不连续的,而将数据集转移到高维空间,仍沿用低维空间的方法找到的高密度区域线性数据点进行聚类,k值的确定则变得容易许多。
输入整个数据集X,计算每个数据点的k近邻图,建立一个N×N的矩阵S,其中数据集X为N维,则矩阵元素Sij的值为:
(1)
如果xi属于xj的k邻域,或xj属于xi的k邻域,则Sij=dij,否则,Sij=0。其中,Sij表示第i个元素和第j个元素之间的相似性度量,dij使用高斯核函数进行计算:
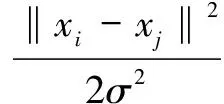
(2)
其中,‖xi-xj‖表示欧氏距离测度;dij表示数据点xi和xj的邻接程度,由此构造了数据集X的邻接矩阵。
由上述邻接矩阵可定义每个数据点的相对密度,通过式(3)求得每个数据点的相对密度:
(3)
对所有数据点以降序方式重新排序,选取相对密度较高的数据点(一般选取密度最大的前96%的数据点作为高密度数据点)对其聚类,确定聚类数目k。
Xseeds={xi|den(xi)>T96,xi∈X}
(4)
2 基于谱聚类模糊的度量相似性
高斯核函数是传统谱聚类算法中用于计算两点间相似性度量的常用方法,是在欧几里得距离的基础上加入尺度参数σ扩展形成的,其聚类结果的好坏受参数影响很大,具有明显的局限性。由于高斯核函数对尺度参数敏感,如以不同的参数挨个尝试去做聚类,不仅增加了设备运算成本还浪费了大量时间,降低了算法效率,因此选取一种良好的相似性度量方法很有必要。文献[16]提出了一种基于路径相似度测量的鲁棒性谱聚类算法(RPB-SC),通过定义高斯核的邻域加权尺度因子计算相似度和以路径聚类思想调节全局相似度,有效减弱高斯核尺度参数的影响,提高聚类性能。实验选取了不受参数影响且稳定性更高的基于谱聚类模糊的相似性度量方法,利用模糊C均值(Fuzzy C-Means,FCM)算法求隶属矩阵,其任意两点间的相似性关系可根据每个数据点对聚类中心的隶属度关系推导求得[17]。
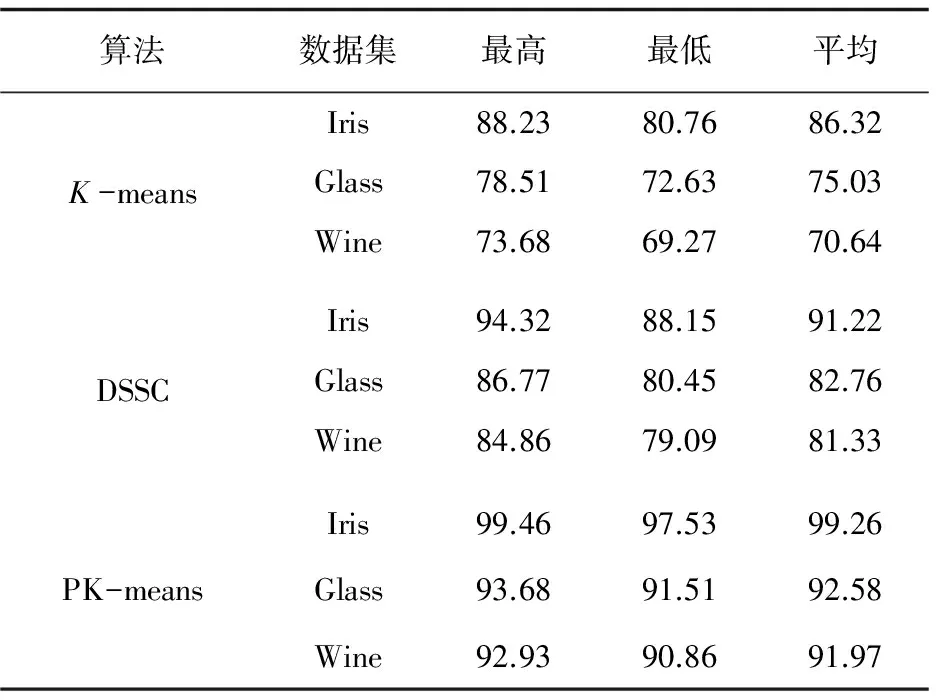
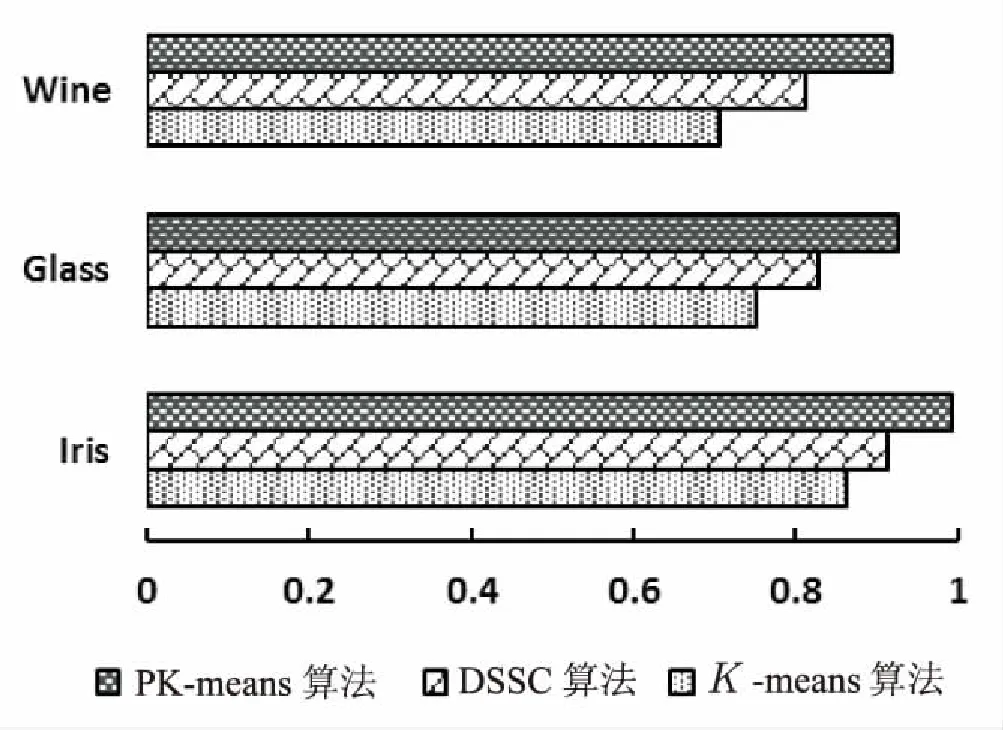
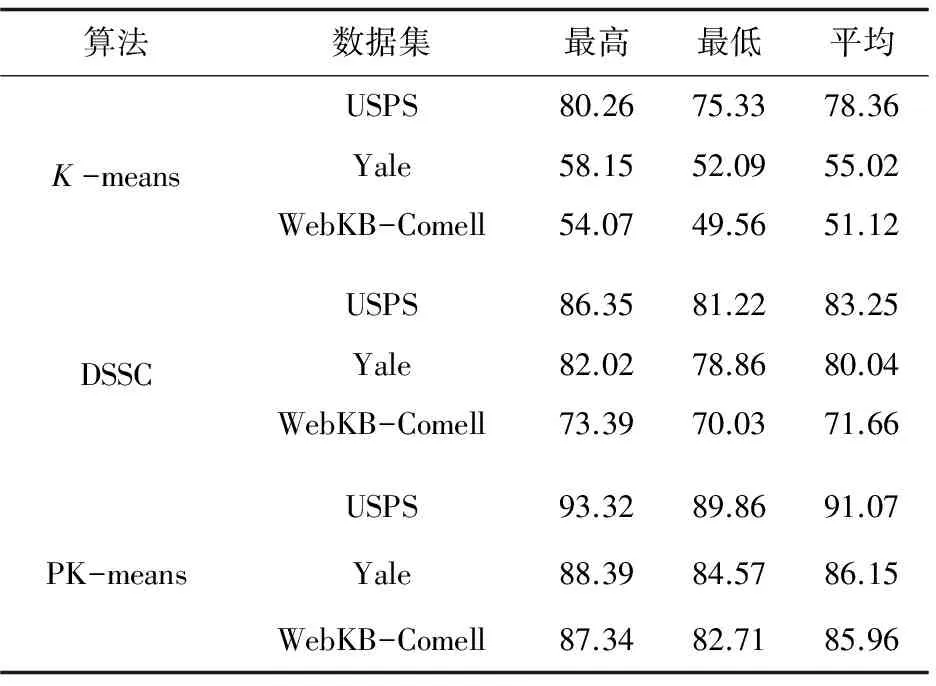
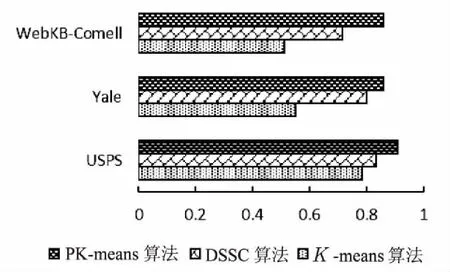
设现有一N维数据集X和C个聚类中心Ci(i=1,2,…,c),1 (5) 其中,uij表示第j个数据点分别属于第i类的程度,用0~1之间的数值表示,当对隶属度矩阵归一化后,该数据集的隶属度总和为1。 (6) 模糊聚类的目标函数最小化后得到的隶属度矩阵为: (7) 其中,U为隶属度矩阵;ci为模糊组I的聚类中心;dij=‖ci-xj‖为数据集ci到各个聚类中心的欧氏距离;m∈[1,∞)是一个控制模糊度的加权指数,影响隶属度矩阵的模糊程度。 构造新的目标函数,此函数是使式(7)达到最小值的一个必要条件: (8) 其中,λj(j=1,2,…,n)是式(6)n个约束式的拉格朗日乘子。 使式(7)达到最小化目标函数的两个特定先决条件为: (9) (10) FCM的最小目标函数通过式(9)、(10)交替更新簇ci的中心和隶属矩阵U,直至目标函数值小于某个阈值或两次目标函数值一个小于某个阈值,则算法停止。其过程可简单描述为:先随机初始化初始聚类中心,然后求隶属度矩阵,再计算目标函数,迭代(FCM聚类算法迭代过程较为简单)。确定隶属度矩阵后,即可确定集群中任意两点的相似性,如果为同一聚类中心,则相似性的概率较大,反之则较小。 基于FCM算法模糊聚类的相异性计算的实现过程如下: Step1:输入经FCM算法计算得到的隶属度和最近的聚类中心数; Step2:按照降序排列隶属度矩阵U中的每一列,获得一个新的矩阵U'; Step4:令Sij=Sji; Step5:输出数据集的模糊相异性情况。 3.1PK-means算法 提出的改良K-means算法是在谱聚类算法的基础上进行扩展的,记作PK-means。由于谱聚类算法具有优秀的处理高维数据的特性,结合K-means算法后能更好地完成对高维非线性数据的聚类。将上述两种聚类算法合二为一,使PK-means算法不仅具有自动确定聚类数目k的能力,同时还引入了谱聚类模糊的度量相似性法则来保证聚类的准确度。其算法过程如下: Step1:确定初始聚类数k,可依据提出的自动确定聚类数目的方法进行计算; Step2:通过FCM模糊聚类的相异性计算方法,确定相似性矩阵S; Step6:利用K-means算法对标准化后的矩阵M'进行聚类。 3.2实验环境和实验数据选取 3.2.1 实验环境 实验选用的平台是Windows 7专业版64位,Intel Core i5-3470 CPU @ 3.20 GHz,8.00 GB内存,1T SATA硬盘,MATLAB R2010b语言编程环境。 3.2.2 UCI实验数据 为验证该算法的高效性和准确率,选取了低维数据集和高维数据集作为实验的数据源,这些数据源均来自国际上专用于测试聚类算法性能的UCI数据库[9]。低维数据源选取了Iris、Glass和Wine,分别为4维、7维和13维,类别数为3、9和3;高维数据源选取了USPS、Yale和WebKB-Comell,抽取的样本数均为800个。其中USPS手写数据集的维数是256,16×16像素的灰度图像,每一数字400幅,类别数为5;Yale人脸数据集的维数是1 024,每个人脸分割的纹理图像是32×32像素,类别数为15;另外,特选取了维数高达4 143,类别数为7的WebKB-Comell文本数据集。实验将使用三种不同的聚类算法,即K-means算法、密度敏感的谱聚类算法(Density-Sensitive Spectral Clustering,DSSC)[18]和PK-means算法,对所选取的多维数据集进行聚类。其中,将选择聚类效果最优的参数进行对比验证,实验次数为30,验证聚类结果的准确率。 3.3低维数据集实验对比分析 选取低维数据集,计算其聚类的正确率,对实验结果取平均值,如表1所示。平均正确率条形图如图1所示。 表1 三种算法处理低维数据集的聚类精度比 % 由表1和图1可以看出,在低维空间时,DSSC算法比传统的K-means算法在聚类方面性能要好,但相较于PK-means算法效率还尚有差距。究其原因,PK-means算法所体现的优势在于,首先DSSC算法的相似性度量是对参数敏感的,而PK-means算法是基于隶属度矩阵,不会选择到敏感的参数;其次,PK-means算法有效地解决了K-means算法中不能高效选取簇的初始数目的问题。此外,这三种算法都有一个共同特点,随着维数的升高,其聚类效果稍有下降,维数越高下降越明显。为了能更好地体现PK-means算法的高效性和准确性,下面将对高维数据集进行同样的类似实验。 图1 三种聚类算法处理低维数据集的平均正确率条形图 3.4高维数据集实验对比分析 选取高维数据集,计算其聚类的正确率,对实验结果取平均值,如表2所示。平均正确率条形图如图2所示。 表2 三种算法处理高维数据集的聚类精度比 % 图2 三种聚类算法处理高维数据集的平均正确率条形图 从表2和图2可以看出,在高维空间,随着数据集维数的增大,聚类的正确率也有所下降。其中,K-means算法聚类正确率受维度数变化下降最为明显,其次是DSSC算法,PK-means算法虽也有影响,但和前两种算法相比,受到的波动则可算之微乎其微。 综上,三种聚类算法处理低维数据集的准确率要高于高维数据集的准确率,而无论是在处理低维数据集还是高维数据集,K-means算法都是最低的,其次是DSSC算法,而PK-means算法优势明显,且维数越高,聚类性能表现越突出。 充分利用K-means算法收敛快和谱聚类算法对数据集维度数不敏感的特点,提出了PK-Means算法。通过高密度数据点计算并对其聚类,可较容易地获得聚类数目k,有效解决了初始聚类中心选择和孤立点的问题;利用模糊的度量元素相异性方法降低了谱聚类算法对参数的敏感性,并采用FCM求隶属度矩阵的方法确定谱聚类算法中的相似度,消除了对敏感参数的选择。实验结果表明,PK-means算法较其他两种算法具有更高的聚类精度与稳定性,尤其对于高维数据更具优势。然而,该算法仍存在着较大的改进空间,当面对多维海量数据时,在实现分布式处理方式并提高集群的运行效率方面仍需要进一步深入研究。 [1] Han Jiawei,Kamber M.Data mining concepts and techniques[M].2nd ed.Beijing:China Machine Press,2006:402-404. [2] Nagpal A,Jatain A,Gaur D.Review based on data clustering algorithms[C]//Proceedings of IEEE conference on information & communication technologies.[s.l.]:IEEE,2013:298-303. [3] 王 慧,申石磊.一种改进的特征加权K-means聚类算法[J].微电子学与计算机,2010,27(7):161-163. [4] Aggarwal C C,Li Yan,Wang Jianyong,et al.Frequent pattern mining with uncertain data[C]//Proceedings of the 15th ACM SIGKDD international conference on knowledge discovery and data mining.New York:ACM Press,2009:29-38. [5] 曹永春,蔡正琦,邵亚斌.基于K-means的改进人工蜂群聚类算法[J].计算机应用,2014,34(1):204-207. [6] Huang Z.Extensions to the k-means algorithm for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery,1998,2(3):283-304. [7] 邢长征,谷 浩.基于平均密度优化初始聚类中心的k-means算法[J].计算机工程与应用,2014,50(20):135-138. [8] 雷小锋,谢昆青,林 帆,等.一种基于K-Means局部最优性的高效聚类算法[J].软件学报,2008,19(7):1683-1692. [9] 韩凌波,王 强,蒋正锋,等.一种改进的k-means初始聚类中心选取算法[J].计算机工程与应用,2010,46(17):150-152. [10] 黄 敏,何中市,邢欣来,等.一种新的k-means聚类中心选取算法[J].计算机工程与应用,2011,47(35):132-134. [11] 谢娟英,郭文娟,谢维信,等.基于样本空间分布密度的初始聚类中心优化K-均值算法[J].计算机应用研究,2012,29(3):888-892. [12] 翟东海,鱼 江,高 飞,等.最大距离法选取初始簇中心的K-means文本聚类算法的研究[J].计算机应用研究,2014,31(3):713-715. [13] 周炜奔,石跃祥.基于密度的K-means聚类中心选取的优化算法[J].计算机应用研究,2012,29(5):1726-1728. [14] 张健沛,杨 悦,杨 静,等.基于最优划分的K-Means初始聚类中心选取算法[J].系统仿真学报,2009,21(9):2586-2590. [15] 周 林,平西建,徐 森,等.基于谱聚类的聚类集成算法[J].自动化学报,2012,38(8):1335-1342. [16] 范 敏,李泽明,石 欣.基于路径相似度测量的鲁棒性谱聚类算法[J].计算机应用研究,2015,32(2):372-375. [17] 孙晓霞,刘晓霞,谢倩茹.模糊C-均值(FCM)聚类算法的实现[J].计算机应用与软件,2008,25(3):48-50. [18] 王 玲,薄列峰,焦李成.密度敏感的谱聚类[J].电子学报,2007,35(8):1577-1581. ResearchonModificationofK-meansSpectralClusteringAlgorithmofMultidimensionalData XIE Zhi-ming1,2,WANG Peng3,HUANG Yan4 (1.Department of Information Engineering,Shanwei Polytechnic,Shanwei 516600,China; 2.Institute of Cloud Computing & Data Center Engineering Design,Shanwei Institute of Innovative Industrial Design,Shanwei 516600,China;3.School of Computer Science and Technology,Southwest University for Nationalities,Chengdu 610041,China;4.School of Computer Science and Technology,Huaiyin Normal University,Huaian 223300,China) Aiming at the problem that the traditionalK-means algorithm cannot determine the initial cluster numberkautomatically and spectral clustering algorithm is sensitive to parameter,a newK-means algorithm based on spectral clustering called PK-means is proposed.It makes improvement and innovation in selection ofkvalues,sorts the calculated high density data points orderly,and then picks out the frontal 96% density point to cluster,so that the number of clusterskcan be obtained with high accuracy.In the meantime,it also selects the unaffected and higher stable similarity measure method based on spectral clustering fuzziness and uses the FCM algorithm for membership degree matrix so as to determine the similarity between data points.The PK-means,K-means and DSSC have been employed to deal with multi-dimensional nonlinear datasets.The experimental results show that whether the selected data source is low dimension or high dimension,the efficiency ofK-means is the lowest,followed by DSSC,and PK-means owns obvious advantages which always has the higher clustering accuracy and stronger robustness than the traditional clustering algorithm.The higher the dimension,the more prominent the clustering performance. K-means algorithm;spectral clustering algorithm;clustering;FCM algorithm;degree of membership matrix TP301.6 A 1673-629X(2017)10-0060-05 2016-10-27 2017-02-20 < class="emphasis_bold">网络出版时间 时间:2017-07-11 国家自然科学基金资助项目(60702075);广东省科技厅高新技术产业化科技攻关项目(2011B010200007);广东省高等职业教育质量工程教育教学改革项目(GDJG2015244,GDJG2015245) 谢志明(1977-),男,讲师,硕士,研究方向为云计算与大数据、算法设计。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1456.068.html 10.3969/j.issn.1673-629X.2017.10.013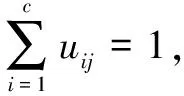
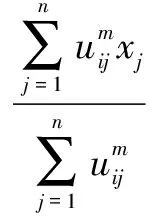
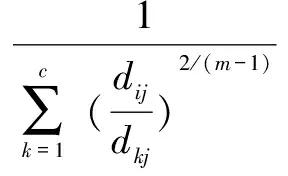
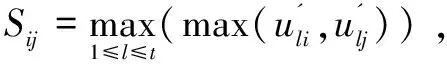
3 算法实现过程及实验结果分析

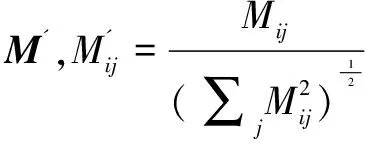
4 结束语
