公元纪年与干支纪年的对应技巧

曾鹏

摘要：

公元纪年和干支纪年是我国现行并用的纪年法。公元纪年，原称基督纪年，亦称西历或西元，是历史年轮演进的顺序代码，是一个无限延伸的数字序号，有“公元前”和“公元后”之分。与公元纪年相关的有“世纪”和“年代”两个概念。干支纪年是以十天干和十二地支顺次对应而组合成的甲历纪年法则，每六十年为一个循环周期，古人用来表示年、月、日和时辰的次序，周而复始，循环不已。

关键词：

公元纪年；干支纪年；推算技巧

中图分类号：K04

文献标识码：A

文章编号：1000-5099（2017）03-0103-05

国际DOI编码：10.15958/j.cnki.gdxbshb.2017.03.17

公元纪年，原称基督纪年，又称西历，即格里历，又译为国瑞历、额我略历、格列高利历、格里高利历，亦称西元，是意大利医生兼哲学家里利乌斯（Aloysius Lilius）對《儒略历》加以改革而编制成的一种历法。公元1582年，教皇格列高利十三世予以批准颁行。“公元”是公历的纪元，产生于公元6世纪，当时，基督徒们极力扩大教会的统治势力，几乎把任何事情都附会于基督教会。公元525年，教徒狄奥尼西为了预先推算7年后（公元532年）“复活节”的日期，提出耶稣出生于古罗马狄奥克列颠纪年之前的248年，主张以耶稣出生之年作为公元纪年的起算点，并把耶稣诞生前、后的日期分别称为“主前”和“主的年份”。这个主张得到了教会的大力支持，公元532年（亚历山大复活节日期每532年为一个循环），教会把狄奥克列颠纪年之前的248年定为“主的年份元年”，率先在教会中推行。近代学者为了淡化其宗教色彩，同时避免非基督徒的反感，而改用“公元”和“公元前”的称谓。18世纪随着西方国家对外扩张，实行殖民统治，西方文化、历法等广泛传播，公元纪年便逐步成为世界多数国家通行的纪年法则。但也有部分国家、地区或民族仍然使用其传统历法，而不采用西元纪年法，世界上几乎所有华人，以及朝鲜、韩国、越南、马来西亚等国家，至今仍然使用中国夏历（又称农历、阴历、殷历、古历、旧历等）来推算传统节日，如春节、端午节、中秋节等；还有一些国家使用伊斯兰纪元、佛教纪元（如泰国使用佛教纪元，公元2016年相当于佛历2559年）、日本纪元、希伯来纪元、波斯纪元、衣索匹亚纪元、印度纪元、伊朗纪元、犹太纪元，还有天文纪年、帝王年号纪元等等纪年法则。

一、公元纪年和干支纪年概说

公元纪年是历史年轮演进的顺序代码，是一个无限延伸的数字序号。公元前的纪年，通常以B.C.（英文Before Christ的缩写）表示，前、后分界不设〇年，从公元前1年起记，逆向推进，如公元前1年庚申，公元前1400年辛丑，公元前2605年丙申等；公元后的纪年定为公元某年，通常以A.D.（拉丁文Anno Domini的缩写）或者C.E.（英文Common Era的缩写）表示。从公元1年起记，顺行记年，如公元1年辛酉，公元2年壬戌，公元3年癸亥，公元1840年庚子，公元1911年辛亥等，公元1年，相当于中国西汉平帝（刘衎）元年。与公元纪年相关的有“世纪”和“年代”两个概念，“世纪”一词来源于拉丁文，意思是100年，即一个世纪为100年。按照常规，公元1年至公元100年为一世纪，公元101年至公元200年为第二世纪……由于没有公元〇年，公元一世纪是公元1年至公元99年共计99年，从二世纪起每个世纪才是100年。这是因为历法业界已经形成的习惯，就是把每个00年作为下一个世纪的第一年，所以，公元二世纪是从公元100年至公元199年，三世纪是公元200年至公元299年，……公元2000年至公元2099年为21世纪，以此类推。

公元前、后世纪的推算原理是一样的，唯一不同的是从绝对值大的向绝对值小的年份顺序排列，如公元前一世纪为公元前99年至公元前1年的99年；公元前二世纪是公元前199至公元前100年，……公元前2299年至公元前2200年为公元前23世纪，以此类推。如何准确判定某一年在哪个世纪呢？这里介绍一个简单的方法（公元前、后相同）：（1）公元年份是两位自然数的，即在1—99年间，则肯定是在公元一世纪里；（2）公元年份是三位自然数的，即在100—999年之间，就在每个世纪第一年的百位数上加上1即可，如公元389年，3+1=4，即为公元4世纪，以此类推。（3）公元年份是四位自然数的，即在1000-9999年之间，就以年份自然数的前两位数（千位和百位）加上1定其世纪数，如公元前1735年，前两位数是17，17+1=18，即为公元前18世纪；又如公元2016年，20+1=21，即为公元21世纪，简称21世纪，以此类推。

在公元纪年的世纪中，又分为早期或称初期、中期、晚期或称未期，或者分为前半期、后半期等。早期，即一个世纪的前30年；中期，则指一个世纪中间的50年；晚期，是一个世纪的后20年；前半期和后半期就是指一个世纪的前、后各50年。“年代”是指一个世纪中的某一个10年，但是，历法业界已经习惯把每个世纪的前20年（公元前、后一个世纪均为前19年）称为某世纪初年；把20—29年称为20年代，30—39年称为30年代，…… 90—99年称为90年代，由此可知，每个世纪实际上又可分为1个初年，8个年代。在世界上，对相隔久远的年代还有千年代的说法，即1000年为一个千年代。上述这些概念已经被人们广泛接受，而且早已运用于實际生活和工作之中。

计算跨公元前、后连续纪年总数的方法。因为公元前、后的分界点不设〇年，故公元前的纪年数是按绝对值由大到小的顺序排列，绝对值最小的是公元前1年。从公元前2000年（含）到公元前1年（含），总年数是2000年，同理，公元纪年按绝对值由小到大依次排列，从公元1年（含）到公元2000年（含），也是整2000年。最简单的方法就是将公元前、后两个积年总数直接相加即得。如果在数轴上计算跨公元前、后的连续纪年总数，则不同于数学中正负数绝对值相加的计算方法，正确的计算方法是：“自公元前某年起至公元某年之总数-1”。因为在数轴上是贯通公元前、后连续计数的，包含了数轴原点“〇”，所以要减去1年。如公元前1525年至公元2015年的总年数为3541年，减去1后实际为3540年。

公元纪年是从西方传入中国的，我国从公元1912年起采用西元的月、日，同时实行中华民国纪年法（公元1912年为民国1年）。1949年9月27日，中国人民政治协商会议第一届全会通过《公元纪年法》，我国从此正式与国际上通用的公元纪年法接轨。

公元纪年和干支纪年是我国现行并用的纪年法。干支纪年是以十天干和十二地支顺次对应而组合成的甲历纪年法则，每六十年为一个循环周期，一般称为“六十甲子”，又称“一花甲子”或“一甲子”，古人用来表示年、月、日和时辰的次序，周而复始，循环不已。我国使用干支纪年历史悠久，黄帝历、颛顼历、夏历、殷历、周历、鲁历合称为古六历，均属于以干支纪年和农历并行的历法。据史载，太昊伏羲氏作甲历，定四时，黄帝命大桡作甲子，至夏商周日臻完善，后来的历代皇帝都很重视修订历法，并广泛运用历法指导农牧畜业生产，研究天象物候。特别值得一提的是，商朝30位帝王全部以天干字样命名，如太甲、祖乙、外丙、武丁、太戊、雍己、盘庚、小辛、外壬等，这种命名用字的方式，很可能与其出生的年份或月、或日、或时辰有关。从中华民族的史书来看，公元1912年以前都是以干支纪年法记载部族、国家史实的，如“辛酉政变”“甲午中日战争”“戊戌变法”“辛丑条约”“辛亥革命”等。由此可见，干支纪年法已经千古流传、根深蒂固，是中华传统文化中的重要组成部分，是中华民族传统文化中的瑰宝。

公元纪年与干支纪年各成体系，又能相互对应换算。由于“六十甲子”的特定循环规律（每六十年循环一次），缺乏明确的线性计数概念，因而造成它很难单独标示某一事物在整体历史发展长河中的准确时段。如大禹元年为丙子年，到底是公元前2205年，还是公元前1605年？还是……的丙子年呢？因为“六十甲子”的每一个循环期内都有一个丙子年，不熟悉古代历史年代的人是根本无法确定的。为了准确掌握干支纪年在历史时空坐标上的确切时点，就必须把公元纪年与干支纪年相对应，同步推移，方可获得准确答案。下面介绍几种对应的方法和技巧只要掌握其中一种方法就能迎刃而解。

二、列表推算法

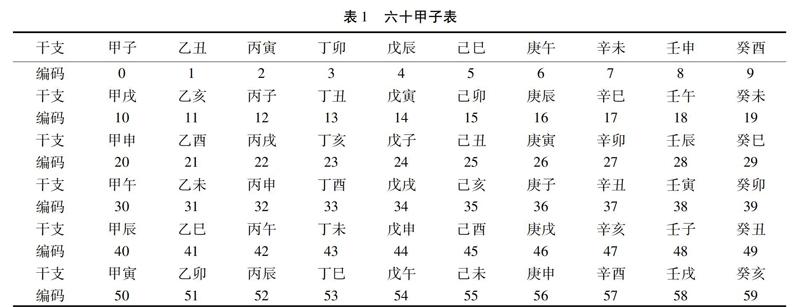
列表推算公元纪年的干支非常直观，基本不会出错，不过所做基础工作量较大。将十天干：甲、乙、丙、丁、戊、己、庚、辛、壬、癸与十二地支：子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥，从头到尾依次一一匹配，反复组合六次，就列出了如表1所示的“六十甲子表”。

在数轴上，公元前纪年（简称“公元前”，或“前”） 以其绝对值由小到大排列，向原点的负方向或说逆向推进，绝对值越大的年份，距离现今的年代越久远。公元前纪年的干支则是由其对应的绝对值大的年份向数轴原点方向依次排列的。公元后纪年（简称公元）与其相对应的干支则是同向并肩向原点的正方向推进，公元纪年年份数的绝对值越大，该年份就越接近现今。

（一）查询公元纪年的干支

现以公元1年与辛酉年为首个平行基准点。从表一可知，公元一世纪，干支在“六十甲子”的第一个循环周期内公元1年辛酉，其编码为57，到公元4年甲子（为计算方便，特向前推1年）共計为4年，因此“4”就成为一个常数。设公元年份数为x，在推查“六十甲子”第一個循环周期内的干支时，设定公式“X-4”，以所得的差数作编码，对应表一中的干支，即为所要查询的公元纪年的干支。例如：查公元50年的干支，需要将年份数50代入公式：50-4=46，查表一，编码46对应庚戌，即公元50年的干支是庚戌。同理可得，公元27年的干支是丁亥（27-4=23，对应干支是丁亥）。“六十甲子”从第二个循环周期起就是60年了，为了运算方便，设“六十甲子”的循环周期次数为“n”（可按查询时段之需，n=1、2……33……等若干次数）。现定基准点为公元4年（甲子年），以“4+60n”所得之和，如公元64、184、484……1204……1804……2164……2404……3004年等均为甲子年，换言之，凡是与60成倍数关系的总数加上4的和数所对应的年份，均为甲子年，这样，就可在表一中快捷地查找到相应年份的干支了。例如查公元1267年的干支。第一步，求查询年甲子循环次数n=1267÷60=21……7（即循环21次，余数不用）；第二步，按照计算公式：4+（60×21）=1264 （可知公元1264年是甲子年）；第三步，已知在表一中甲子年对应编码是0，从公元1264年（含当年）到公元1267年（含当年）顺次移动4年，即从编码0到编码3，对应丁卯，即公元1267年为丁卯年。

（二）查询公元前纪年干支

公元前1年的干支为庚申，在表一中的编码是56，即从干支甲子顺数直到庚申，共计57年（公元前纪年在《六十甲子》第一个循环周期内只有57年，另3年为公元纪年），或从编码56（庚申）起，倒数至编码“0”（甲子），甲子年即为公元前57年，从第二个甲子周期起每60年循环一次。现以“57”为常数，设定的公式“57+60n”，据此计算出的年份数所对应的干支必定是甲子年。以这个甲子年的年分数减去查询年的年分数，以所得的差为查询编码数，即为公元前某年份所对应的干支。例如求公元前2205年的干支。第一步，求查询年甲子循环次数n=2205÷60=36……45（循环36次，余数不用）；第二步，求查询年的编码：57+（60×36）-2205=12（12即为查询年的编码）；第三步，在表一中找到编码12，对应丙子，即公元前2205年的干支为丙子。再比如求公元前725年的干支，第一步，求查询年甲子循环次数n=725÷60=12……5 （循环12次，余数不用）；第二步，求查询年的编码：57+（60×12）-725=52（52即为查询年的编码）；第三步，在表一中找到编码52，对应丙辰，即公元前725年的干支是丙辰。

三、技巧查对法

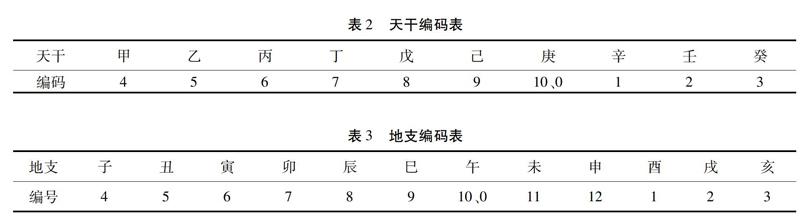
所谓技巧查对干支，就是用一些简单的算术方法来查对公元前、后纪年所对应的干支，关键问题就是记住天干、地支的编码和对应方法。我们将十天干和十二地支分别列表、编号（表2、表3），作为公元纪年与干支纪年对应求解的工具。

（一）求公元纪年的干支

推算公元某年干支的基本方法：（1）查询公元1—10年的干支，以年分数本身作编码，分别直接在表2、表3中定查询年的干支，如公元8年的干支为戊辰。查询公元11、12年的干支，以查询年之年分数末位数作编码，在表2中定天干，以查询年之年分数以本身作编码，在表3中定查询年的地支，如公元12年的干支为壬申。（2）确定>12的年分的天干，以查询年之年分数的末位自然数作编码，该编码所对应的天干即为查询年的天干。（3）确定>12的年分的地支。设年份数为x，以x÷12，所得的商不用，取余数作为编码，表三中相同编码所对应的地支即为该年的地支。例如，求公元5年的干支，公元5年，以5作编码，查表二，编码5对应天干乙，即定天干为乙；查表三，编码5对应地支丑，所以公元5年的干支是乙丑。同样的，求公元1934年的干支，公元1934年的末位数是4，即编码为4，查表二，编码4对应天干甲，甲即为该年的天干；1934÷12=161……2 余数2，即编码为2，查表三，编码2对应地支戌，所以公元1934年的干支是甲戌。

（二）求公元前纪年的干支

推算公元前某年干支的基本方法：（1）因为天干共十个，故以10+1=11作为常数，用公式11-前纪年末位自然数，以所得的差为编码数，对应表二中的天干，即为所要查询的天干；（2）第一步，设公元前纪年的年份数为，用y÷12，所得的商不用，取其余数备用；第二步，因为地支一共有十二个，故以12+1=13作为常数；第三步，用13-余数，以所得的差为编码，对应表三中的地支，即为要查询的地支。（3）公元前纪年仅一位数的年份，直接以11-前纪年数、13-前纪年数，分别以其差值作为编码，在表二、三中对应查取即可。现举例加以说明，例如求公元前2314年的干支，求天干，根据公式11-4=7，即编碼为7，查表二，编码7对应天干丁；求地支：2314÷12=192……10，13-10=3，即编码为3；查表三，编码3对应地支亥，故公元前2314年的干支为丁亥。再比如，求公元前45年的干支，查天干：11-5=6 ，即编码为6；查表二，编码6对应的天干是丙；查地支：45÷12=3……9，13-9=4，即编码为4；查表三，编码4对应地支子，故公元前45年的干支为丙子。

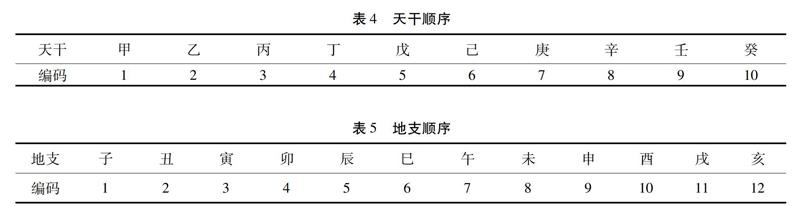
公元前纪年对应的干支，还可用以下方法进行推算。首先按照天干、地支的顺序分别列表、编码，作为本方法使用的工具（表4、表5）：

求天干。我們设定一个常数8，设公元前某年的末位数为m，设其差值为k。用公式：

8-m=k，分下面几种情况：（1）k>〇，就以k作为编码，按顺序直接对应表四中的天干即得解。（2）k≤〇，就用k-1，以所得的差值作编码，在表四中从编码10起倒数定天干。（3）k≤〇，也可用k+10所得的和作编码，在表四中顺向对应查对天干。

求地支。以y÷12，所得的商数不用，取其余数备用。分以下几种情况：（1）所得余数<10，第一步，以10-余数；第二步，以所得的差数作编码，按顺序在表五中查对地支。（2）所得余数≥10，就以10-余数，以其差值在表五中从12（亦作“0”）起倒查所对应的地支。（3）所得余数≥10，再引入一个常数22，用22-余数，用所得的差作编码，按顺序在表五中查定地支。现求解举例如下：

例1.周康王元年是公元前1067年，查该年的干支。求天干：8-7=1（1>〇），即编码为1，查表4，可知1对应天干甲；求地支，1067÷12=88……11，11>〇），以“方法二”之2“求地支”中的方法⑵：10-11=-1，即编码为-1，在表5中倒查地支为戌。以“方法二”之2“求地支”中的方法⑶：22-11=11，11即为编码。在表五中顺查地支为戌。故确定周康王元年，公元前1067年的干支为甲戌。

例2.查齐灵公20年，即公元前562年的干支求天干：8-2=6 （6>〇），即编码为6，查表四，编码6对应天干己；求地支：562÷12=46……10 （10>〇），以“方法二”之2“求地支”中的方法⑵：10-10=0，即编码为0（亦即12），在表五中对应地支为亥。以“方法二”之2“求地支”中的方法⑶：22-10=12 12即为编码，在表五中对应地支为亥，故确定齐灵公20年，公元前562年的干支为己亥。

参考文献：

[1]胡志明，张笑恒.不可不知的2008个中华文化常识[M].北京：中国电影出版社，2007.

[2]刘元.趣说万事由来[M].哈尔滨：哈尔滨出版社，2008.

（责任编辑：王勤美）