m-END误差下回归模型加权估计的相合性

鲁 俊，肖 潇，陶浩然，乔旭东，吴秋月，杨文志*

（安徽大学 a.文典学院；b.数学科学学院，合肥，230009）

m-END误差下回归模型加权估计的相合性

鲁 俊a，肖 潇a，陶浩然a，乔旭东b，吴秋月b，杨文志b*

（安徽大学 a.文典学院；b.数学科学学院，合肥，230009）

m-END随机变量是一类很弱的负相依随机变量，它包含了NA随机变量、NOD随机变量和END随机变量。本文基于误差为m-END序列，研究非参数回归模型未知参数的加权估计，获得了加权估计的收敛性，包括矩相合性收敛速度和完全相合性收敛速度。作为应用，给出非参数回归模型未知参数近邻权估计的矩相合性收敛速度和完全相合性收敛速度。

回归模型；END随机变量；矩相合性；完全相合性

Liu[1]给出如下相依随机变量END随机变量的概念。

定义1 对随机变量序列X1,X2,…,Xn,…，如果存在一正常数M＞0，满足对所有n≥1和所有实数x1,x2,…,xn,都有

则称X1,X2,…,Xn为END的。进一步，如果对所有n≥1,X1,X2,…,Xn，为END随机变量，则称{Xn,n≥1}为END随机变量序列。

如果在定义1中每个取+∞和-∞，易知控制系数M≥1。Liu给出了END随机变量的定义及一些例子[1]。当M=1时，END随机变量就是Lehmann给出的著名NOD随机变量[2]，而NOD随机变量包含了NA随机变量[3]。有关NA、NOD及相关的随机变量的介绍，可参见文献[4-10]及相关引用文献。另一方面，基于m相依和NA随机变量概念，Hu等给了m-NA随机变量的概念，并获得了其完全收敛性结果[11]。受Hu等[11]的启发，Wang等[12]给了m-END随机变量概念。

定义2 对某个固定的整数m≥1，如果对任意的n≥2和任意i1,i2,…,in，当为END的，则称随机变量{Xn,n≥1}为m-END的。

作为应用，Wang等研究了m-END误差下回归模型未知参数加权估计的完全收敛性[12]。受上述文献的启发，本文继续研究m-END误差下回归模型估计的相合性问题，获得加权估计的矩收敛速度和完全收敛速度，推广了已有文献的结果。

下面我们考虑固定设计下的非参数回归模型

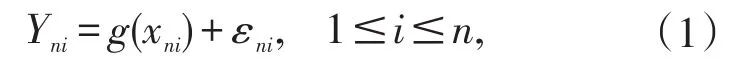
其中xn1,xn2,…,xnm为已知的固定设计点列，且都属于A⊂Rr,r≥1,εn1,εn2,…,εnn为m-END随机误差，g(·)为未知的实函数。假设对所有n≥1,(εn1,εn2,…,εnn)与(ε1,ε2,…,εn)同分布。下面给出未知函数g(·)的加权函数估计量：

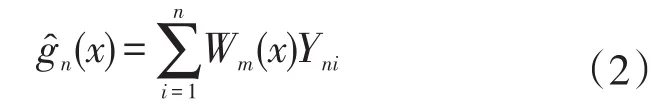
其中，Wm(x)=Wm(x;xn1,…,xnn)为权函数。

有关非参数回归模型的研究很多。例如Tran等获得了线性误差下加权估计(x)的渐近正态性[13]；Liang和Jing获得了NA误差下加权估计(x)的渐近正态性[14]；Yang等给出NOD误差下加权估计(x)的矩相合性和强收敛速度[15]；Wang等给出END误差下加权估计(x)的完全相合性[16]，等等。更多回归模型和统计推断知识，可参见文献[17，18]。本文将考虑误差为m-END误差下非参数回归模型（1）的未知参数g(x)加权估计(x)的渐近性质，获得了加权估计的矩相合性和完全相合性，给出它们的收敛速度。作为应用，给出未知参数近邻权估计量的矩相合性收敛速度和完全相合性收敛速度，具体见第2节主要结论。我们推广了已有文献的结论，具体见注释1。最后一些引理及其定理的证明见第3节内容。

为叙述方便，本文记C,C1,C2,…,C(p),C(p,m),C(p,m,M)为不依赖于n的正常数，I(A)表示集合A的示性函数，‖x‖记为向量x的欧式范数，logn=logmax(n,e)。

1 主要结论

在非参数回归模型（1）中，对某个p≥1和任意固定的x∈A，权函数Wni(x)=Wni(x;xn1,…,xnn)的假设条件如下

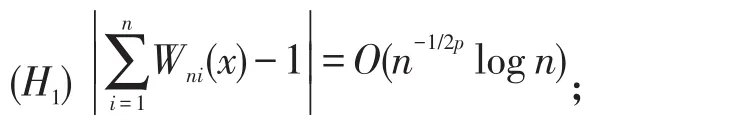
(H2)对所有n≥1，存在一正数C满足

获得g(·)的加权估计(x)的矩相合性收敛速度和完全相合性收敛速度。

定理1 在回归模型（1）中，假设{εn,n≥1}为同分布的m-END序列，且满足Eε1=0，E|ε1|2p＜∞，其中p≥1。假设条件(H1)～(H3)满足，g(x)函数在点x∈A的邻域满足局部莱布利兹条件，则有

进一步，如果E|ε1|2p+2＜∞，有

作为定理1的一个应用，我们给出了g(x)的近邻权函数估计的矩相合性和完全相合性。不失一般性，取A=[0,1],xni=i/n，i=1,2,…,n，对x∈[0,1]，将|xn1-x|,|xn2-x|,…,|xnn-x|按大小重新排序。如果，则规定当i＜j时，|xni-x|排在|xnj-x|之前。设1≤kn≤n，定义回归模型（1）中的g(x)近邻权函数估计

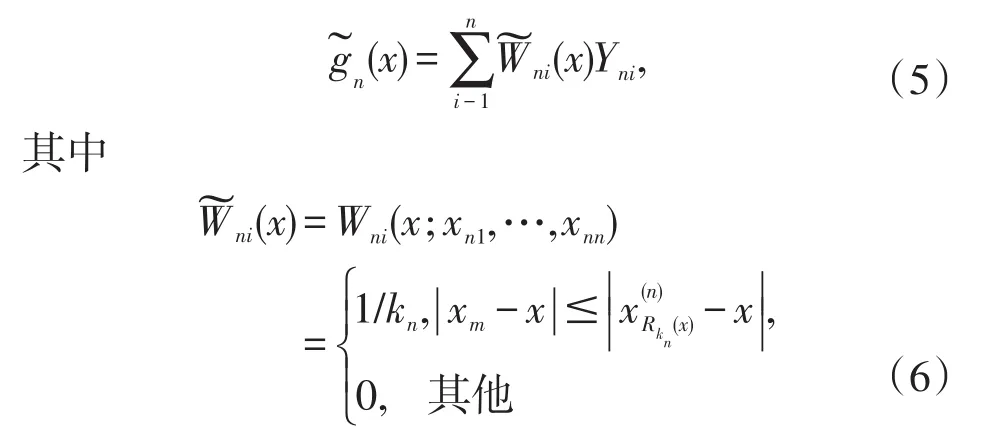
基于上面的符号，应用定理1，获得如下推论。

推论1 在回归模型（1）中，假设{εn,n≥1}为同分布的m-END序列；存在某个p＞3/2，满足Eε1=0,E|ε1|2p＜∞；g(x)函数在点x∈[0,1]的邻域满足局部莱布利兹条件。取kn=[n1/2p]，其中[·]为取整符号，则

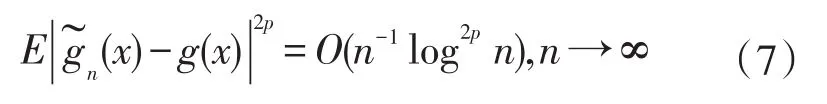
进一步，如果E|ε1|2p+2＜∞，有

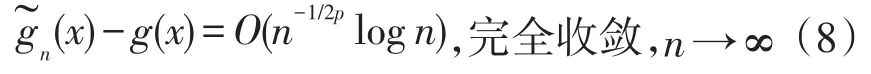
注1 一方面，矩相合性和强相合性不能相互推导，故本文在相同假设条件下分别获得非参数回归模型（1）未知参数加权估计的矩相合性收敛速度和完全相合性收敛速度，具体见（3）式、（4）式、（7）式和（8）式；另一方面，在权函数满足一些条件下，Yang等[15]讨论了误差为NOD（矩条件满足时g(·)的加权估计(x)的矩相合性、一致矩相合性、强相合性和强收敛速度（见其定理2.1-2.4）；Wang等[16]讨论了误差为END（矩条件满足E|ε1|2p＜∞,p≥1）时加权估计(x)的完全相合性，但未讨论其收敛速度（见其定理1.2）；Wang等[12]讨论了误差为m-END（矩条件满足E|ε1|max(2,2/s)＜∞,s≥1/2）时加权估计(x)的完全收敛性，但同样未讨论其收敛速度（见其定理4.1）。受上述文献启发，本文讨论了m-END误差下加权估计(x)的矩相合性和完全相合性，分别给出它们的收敛速度，具体见定理1和推论1。由于m-END随机变量包含NA随机变量、NOD随机变量、END随机变量，所以我们推广了Yang等[15]的定理2.1-2.4、Wang等的定理1.2和Wang等[12]定理4.1到误差为m-END场合，并获得非参数回归模型未知参数加权估计的矩相合性收敛速度和完全相合性收敛速度。

2 引理及定理1的证明

引理1[12]假设X,X,…,X是m-END随机变量，f1(·),f2(·),L,fn(·)对所有变元是非降或非增的Borel函数，则f1(X1),f2(X2),…,fn(Xn)仍是m-END随机变量，控制系数M不变。

引理2[19]假设是END随机变量，满足EXn=0,|Xn|≤dn,a.s.,n≥1,其中{dn,n≥1}为一正数序列。记,则对任意的ε＞0有

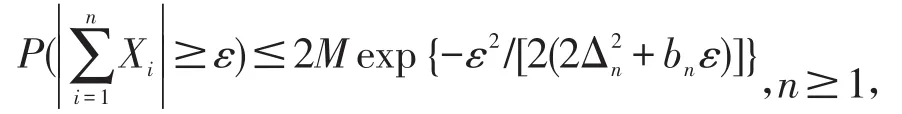
其中M为控制系数。

推论2 假设{Xn,n≥1}是m-END随机变量，满足EXn=0|Xn|≤dn,a.s.,n≥1，其中{dn,n≥1}为一正数序列。记,则对任意的ε＞0有

其中M为引理2所定义。

证明 由于Xn,n≥1为m-END随机变量，所以有m-END定义知，可将{Xn,n≥1}分解为m个END序列，即

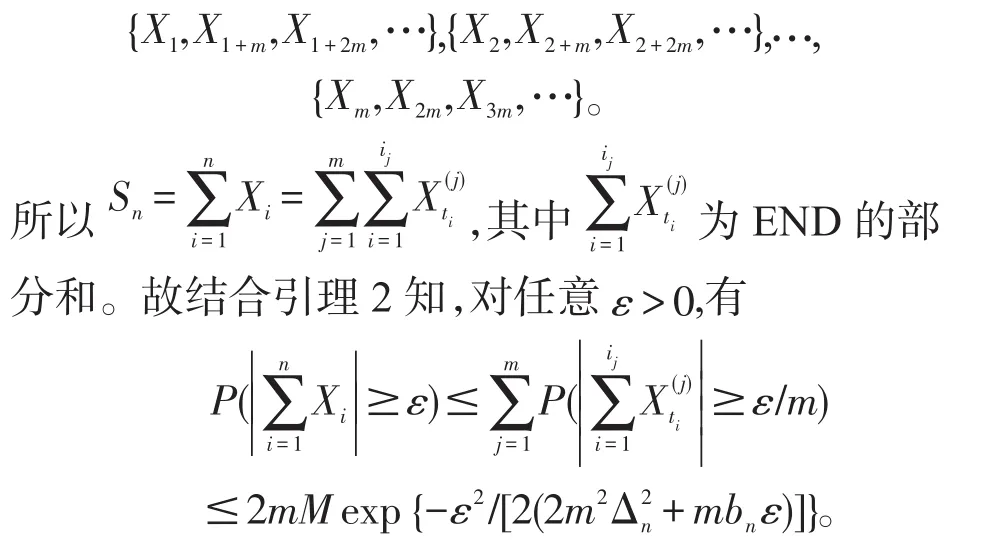
证毕。

引理3[20]设{X,n≥1}是END随机变量，满足EXn=0和E|Xn|p＜∞,n≥1，其中p≥2,则对所有n≥1有

其中,C(p,M)为不依赖于n的正常数。

推论3 设{Xn,n≥1}是m-END随机变量，满足EXn=0和E|Xn|p＜∞，n≥1，其中p≥2,则对所有n≥1有

其中，C1(p,m,M)为不依赖于n的正常数。进一步，如果{ani,1≤i≤n,n≥1}为一实数阵列，则

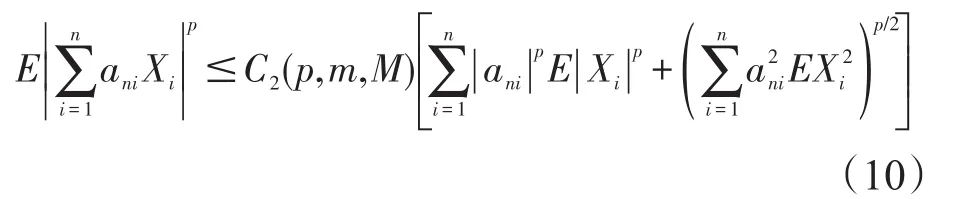
其中，C2(p,m,M)为不依赖于n的正常数。

证明 由于m-END序列可分解为m个END序列，再结合Cr不等式和引理3，易得（9）式。另一方面，对固定的n≥1，由引理1知和仍为m-END随机变量，控制系数不变。进一步，由于函数f(x)=xp/2关于x≥0是增函数，其中p≥2。故有

最后结合（9）式，易得（10）式，证毕。

定理1的证明对于固定的x∈A，由引理1知，和仍为m-END序列，控制系数不变。结合，不失一般性，我们在证明过程中假设Wni(x)≥0。类似于在Yang等[15]的（4.2）的证明，由(H1)～(H3)，对x∈A，有

由于对所有n≥1，由于(εn1,εn2,...,εnn)与(ε1,ε2,...,εn)同分布，且ε1,ε2,...,εn同分布。故由（2）式，条件(H2)、Eε1=0、E|ε1|2p＜∞，对x∈A，应用推论3的（10）式得

另一方面，结合Cr不等式，有

所以由（11）式至（13）式知（3）式成立。

接下来我们将证明（4）式。由（11）式，为证（4）式，只需证明

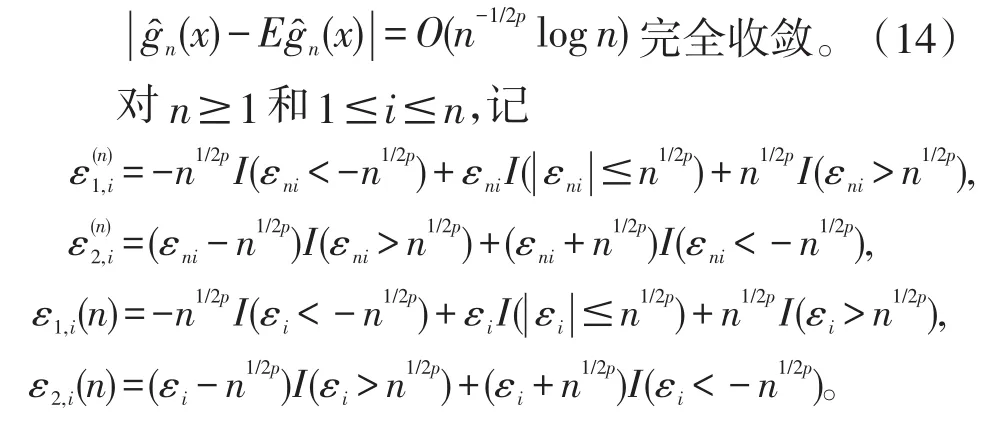
对于所有固定的n≥1，由于(εn1,εn2,εn3,...,εnn)与(ε1,ε2,ε3,...,εn)同分布及ε1,ε2,...,εn同分布，知Eεni=Eεi=Eε1=0，从而有

因此，由(H2)和E|ε1|2p+2＜∞(p≥1)知，

由于{Wni(x)(ε1,i(n)-Eε1,i(n),1≤i≤n)}仍为m-END随机变量，控制系数不变，因此由推论2知，存在充分大的正数C满足

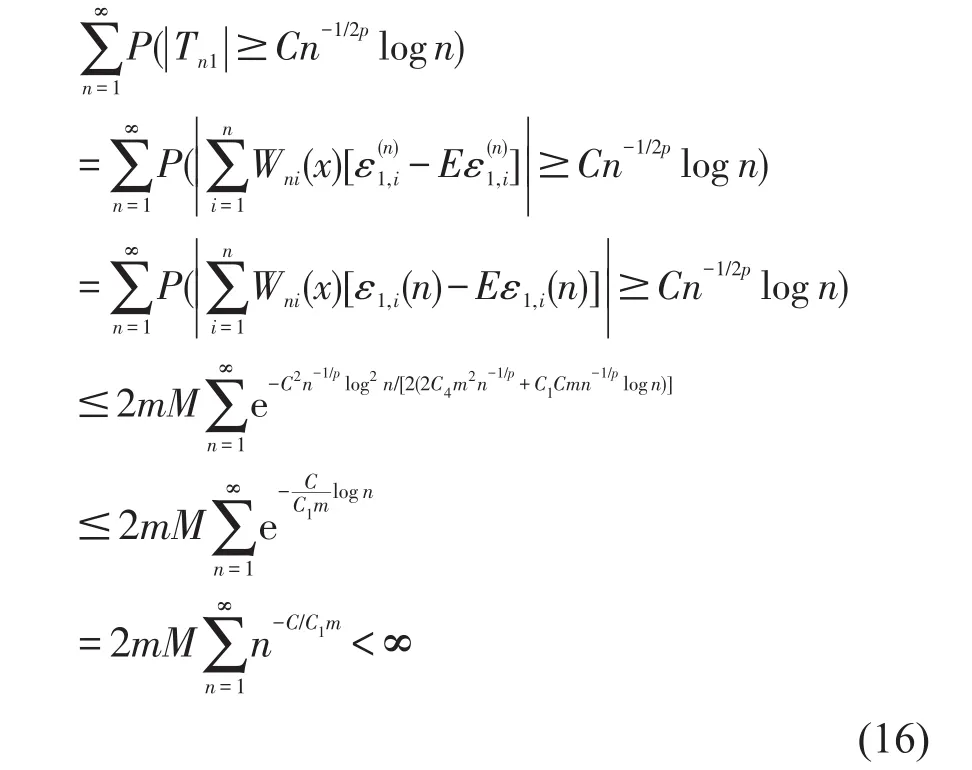
另一方面，根据(H2),E|ε1|2p+2＜∞(p≥1)以及Markov不等式,知

因此，由（15）式至（17）式知（14）式成立。故（4）式证毕。

推论1的证明对于每个x∈[0,1]，由Ri(x)的定义及xni和kn=[n1/p]的选取，有

显然，对于任何s＞0，若s(1-3/2p)≥1/2p，有p≥(3s+1)/2s＞3/2。所以对p＞3/2和任意的s＞0，有

由于函数g(x)在点x∈[0,1]的邻域满足局部莱布利兹条件，由（6）式和（18）式至（20）式，我们可以验证条件(H1)～(H3)都是满足的。因此，应用定理1，立即获得推论1。故（7）式和（8）式证毕。

[1]Liu L.Precise large deviations for dependent random variables with heavy tails[J].Statistics and Probability Letters,2009,79(9)：1290-1298.

[2]Lehmann E L.Some concepts of dependence[J].Annals of Mathematical Statistics,1966,37(5)：1137-1153.

[3]Joad-Dev K,Proschan F.Negative association of random variables with applications[J].Annals of Statistics,1983,11(1)：286-295.

[4]胡太忠.随机变量的负超可加相依及其应用[J].应用概率统计,2000,16(2)：133-144.

[5]Wu Q Y.A strong limit theorem for weighted sums of sequences of negatively dependent random variables[J].Journal of Inequalities and Applications,2010,Article ID 383805,8 pages.

[6]林正炎,陆传荣,苏中根.概率极限理论基础[M].北京：高等教育出版社,1999：78-118.

[7]吴群英.混合序列的概率极限理论[M].北京：科学出版社,2006：132-205.

[8]Bulinski A V,Shaskin A.Limit theorems for associated random fields and related systems[M].Singapore：World Scientific,2007：1-160.

[9]Rao P B L S.Associated sequences,demimartingales and nonparametric inference[M].Basel：Birkhaauser,Springer,2012：1-30.

[10]Oliveira P E.Asymptotics for associated random variables[M].Berlin Heidelberg：Springer-Verlag,2012：3-33.

[11]Hu T C,Chiang C Y,Taylor R L.On complete convergence for arrays of rowwise m-negatively associated random variables[J].Nonlinear Analysis,2009,71(12)：1075-1081.

[12]Wang X J,Wu Y,Hu S H.Exponential probability inequality for m-END random variables and its applications[J].Metrika,2016,79(2)：127-147.

[13]Tran L,Roussas G,Yakowitz S,et al.Fixed-design regression for linear time series[J].Annals of Statistics,1996,24(3)：975-991.

[14]Liang H Y,Jing B Y.Asymptotic properties for estimates of nonparametric regression models based on negatively associated sequences[J].Journal of MultivariateAnalysis,2005,95(2)：227-245.

[15]Yang W Z,Wang X J,Wang X H,et al.The consistency for estimator of nonparametric regression model based on NOD errors[J].Journal of Inequalities and Applications 2012,2012：140,pages 13.

[16]Wang X J,Zheng L L,Xu C,et al.Complete consistency for the estimator of nonparametric regression models based on extended negatively dependent errors[J].Statistics,2015,49(2)：396-407.

[17]陈希孺.数理统计引论[M].北京：科学出版社,1981：439-532.

[18] 陈希孺,陈桂景,吴启光,等.线性模型参数的估计理论[M].北京：科学出版社,2010：30-155.

[19]Yang W Z,Xu H Y,Chen L,Hu S H.Complete consistency of estimators for regression models based on extended negatively dependent errors[J].Statistical Papers,First Online：28 April 2016,DOI 10.1007/s00362-016-0771-x

[20]Shen A T.Probability inequalities for END sequence and their applications[J].Journal of Inequalities and Applications,2011,2011：98,pages 12.

Consistency of weighted estimator of regression model based onm-END errors

LU Juna,XIAO Xiaoa,TAO Hao-rana,QIAO Xu-dongb,WU Qiu-yueb,YANG Wen-zhib*
(a.Wendian College;b.School of Mathematical Sciences,Anhui University,Hefei Anhui230039,China)

m-END random variables are weakly dependent random variables,which contain NA random variables,NOD random variables and END random variables.In this paper,we investigate the weighted estimator of nonparametric regression model based onm-END errors.Some results of consistency such as mean convergence rate and complete convergence rate are obtained.As an application,the nearest neighbor weight estimator of nonparametric regression model is studied and mean convergence rate and complete convergence rate are presented.

regression model;END random variables;mean consistency;complete consistency

O212.7

A

1004-4329（2017）03-030-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）03-030-05

2017-04-14

国家自然科学基金(11501005，11671012)；安徽省自然科学基金(1508085J06)资助。

杨文志(1982- )，男，博士，副教授，研究方向：概率论与数理统计。