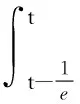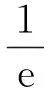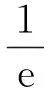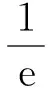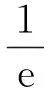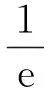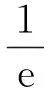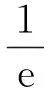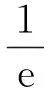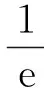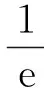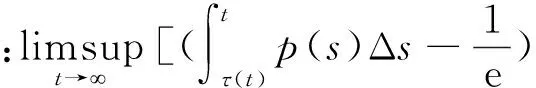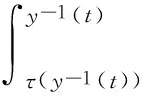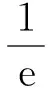时标上一类具时滞的动力方程的新的非振动准则

刘兰初，王 佩

(湖南工程学院 理学院, 湘潭 411104)

时标上一类具时滞的动力方程的新的非振动准则

刘兰初，王 佩

(湖南工程学院 理学院, 湘潭 411104)

考虑了时标上时滞动力方程xΔ(t)+P(t)f(x(τ(t)))=0,t≥t0∈T.的非振动性，获得新的非振动解的存在条件.其中P(t),τ(t)∈Crd([t0,.)，R+)，R+=[0,)，f(u)·u>0，τ(t)是非减函数.当T=R,T=Z，f(u)=u时，是该方程的特殊情形，获得的结论是对已有结果的改进与推广.

时标; 时滞; 非振动准则 ；Δ导数

1 预备知识

Stefan Hilger[1]对时标上时滞动力型方程的开创性研究,引起了广泛关注[2-10].时标上的动力方程不仅能够统一微分方程和离散方程，还能揭示更为复杂的动力系统[7-10]，例如在昆虫数量模型、神经网络模型、流行病传播模型等等中都有广泛应用.

首先给出一些基本定义，详见[1-4]将离散和连续形式统一起来的时标(实数R的任意一个非空闭子集称作一个时标，本文以符号T表示)．常用的集合，如R,Z,N,[0,1]∪N，都是时标.

对于函数f:T→R,如果对任意的ε>0，存在U的某一邻域，即U=(t-δ,t+δ)∩T，使得

|[f(σ(t))-f(s)]-fΔ(t)[σ(t)-s]|≤ε|σ(t)-s|

成立，则称为f在t处是可导的，这样的导数称作Δ导数或者Hilger导数.

本文考虑时标上时滞动力方程

xΔ(t)+P(t)f(x(τ(t)))=0,t≥t0∈T.

(1)

其中P(t),τ(t)∈Crd([t0,.)，R+)，R+=[0,)，f(u)·u>0，τ(t)是非减函数.当T=R,T=Z，f(u)=u时，方程(1)已有一些非振动准则[11-12]，本文将这些结果推广到一般的时标上，并获得新的非振动准则.

2 主要结果

引理1[3]若方程(1)存在最终正解当且仅当相应方程

xΔ(t)+P(t)f(x(τ(t)))≤0(t≥t0)

存在最终正解.

引理2[5,6]设P(t)∈Crd([t0,.)，R+)，考虑二阶方程

yΔ2(t)+P(t)f(y(t))=0,t≥t0

(2)

则方程(2)存在最终正解当且仅当

(3)

其中t充分大.

定理1 如果

(4)

且二阶方程

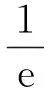
(5)

存在最终正解，则方程

xΔ(t)+f(x(τ(t)))=0,t≥t0∈T.

(6)

存在最终正解.

证明设y(t)是方程(5)的最终正解，由(2)-(4)知存在T≥t0，使得：

(7)

设u(t)=yΔ(t)，显然u(t)>0,uΔ(t)≤0，且

(8)

定义

(9)

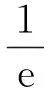
t)u(s)Δs+2ey(T)≤ω(t)-

ω(t)-u(t)

即:

(10)

v0(t)=ω(t),t≥T,vn(t)=

由归纳，有：

u(t)

1,2,...

u(t)≤vn(t)≤ω(t)=2ey(t),t≥T

(11)

且

(12)

(12)代人(5),有

或者

(13)

(14)

将上式代入(14)有

zΔ(t)+f(z(τ(t)))≤0,

(15)

t足够大.这表明不等式(15)有一最终正解，由引理1知相应的方程(6)有最终正解.

注释：当方程(1)中P(t)=1,即为方程(6).

定理2 假设(4)成立，且

(16)

成立，则方程(1)有一最终正解.证明类似与定理1.(略)

定理3 假设存在0t0，使得

(17)

则方程(1)存在最终正解.

[1] S. Hilger. Analysis on Measure Chains A Unified Approach to Continuous and Discrete Calculus[J]. Results in Matematics 1990(18):18-56.

[2] S.H.Saker. Oscillation of Second-order Nonlinear Neutral Delay Dynamic Equations on Time Scales[J].Journal of Computational and Applied Matematics, 2005, 39(3): 377-396.

[3] J.S..Yu,Z.C.Wang,B.G.Zhang,X.Z.Qian.Oscillation of Differential Equations with Deviating Ayguments[J].Panamer Math,1992(2):59-78..

[4] 杨 军，张玉静.时标上二阶混合型边值问题的正解存在性[J].应用数学学报，2008,31(4): 592-598.

[5] E.Hille，Non-oscillation Theorems,Trans.Amer.Math.Soc.1948(64):234-252.

[6] M.K.Kwong,Oscillation of First Order Delay Equations[J].Math.Anal.Appl，1991(156): 274-286.

[7] 刘光辉,夏文华.测度链上一阶中具有多时滞的非线性中立型泛函微分方程的振动性[J].湖南工程学院自科版,2011，21(4)：35-37.

[8] Xun-huan Deng,Qi-ru Wang, Zhan Zhou. Oscillation Criteria for Second Order Nonlinear Delay Dynamic Equations on Time Scales[J].Journal of Computational and Applied Matematics, 2015(269): 834-840.

[9] Qinglong WangZhijun Liu. Existence and Stability of Positive Almost Periodic Solutions for a Competitive System on Time Scales[J]. Matematics and Computers in Simulation, 2017(1): 34-40.

[10] Quanxin Cheng, Jinde Cao. Synchronization of Complex Dynamical Networks with Discrete Time Delays on Time Scales[J].Neurocomputing, 2015,151(2):729-736.

[11] Jianhua,Xianhua Tang. New Nonoscillation Criteria for Delay Differential Equations[J].Math.Anal,2004(290): 1-9.

[12] Xiaoping Wang. Oscillation for Higher Order Superlinear Rdelay Differential Equations with Unstable Type[J].Math.Anal,2004(289): 379-386.

NovelNonoscillatoryCriteriaforDelayDynamicEquationonTimeScales

LIU Lan-chu, WANG Pei

(College of Science, Hunan Institute of Engineering, Xiangtan 411104, China)

Considering the delay dynamic equationsxΔ(t)+P(t)f(x(τ(t)))=0,t≥t0∈T. WhereP(t),τ(t)∈Crd([t0,.),R+)，R+=[0,),f(u)·u>0,τ(t)is nondecreasing, novel nonoscillation criteria are obtained. Our results as a special case whenT=R,T=Z,f(u)=u, are involved improve some nonoscillation results.

time scales; delay; nonoscillatory criteria; delta differential

O175.1

A

1671-119X(2017)03-0040-03

2017-03-02

湖南省教育厅科研资助项目(13C188).

刘兰初(1972-),女,硕士，副教授，研究方向：泛函微分方程及其应用.