粒子群优化的移动机器人路径规划算法

韩 明，刘教民，吴朔媚，王敬涛

(1.石家庄学院 计算机科学与工程学院，石家庄 050035; 2.燕山大学 信息科学与工程学院，河北 秦皇岛 066004)

(*通信作者电子邮箱han_ming2008@126.com)

粒子群优化的移动机器人路径规划算法

韩 明1,2*，刘教民2，吴朔媚1，王敬涛1

(1.石家庄学院 计算机科学与工程学院，石家庄 050035; 2.燕山大学 信息科学与工程学院，河北 秦皇岛 066004)

(*通信作者电子邮箱han_ming2008@126.com)

针对移动机器人在复杂环境下采用传统方法路径规划收敛速度慢和局部最优问题，提出了斥力场下粒子群优化(PSO)的移动机器人路径规划算法。首先采用栅格法对机器人的移动路径进行初步规划，并将栅格法得到的初步路径作为粒子的初始种群,根据障碍物的不同形状和尺寸以及障碍物所占的地图总面积确定栅格粒度的大小，进而对规划路径进行数学建模；然后根据粒子之间的相互协作实现对粒子位置和速度的不断更新；最后采用障碍物斥力势场构造高安全性适应度函数，从而得到一条机器人从初始位置到目标的最优路径。利用Matlab平台对所提算法进行仿真，结果表明，该算法可以实现复杂环境下路径寻优和安全避障；同时还通过对比实验验证了算法收敛速度快，能解决局部最优问题。

栅格法；粒子群优化；路径规划；步进因子；适应度函数

0 引言

智能机器人研究不断取得新的成果，机器人应用也越来越多地渗透到社会的各个领域。在智能机器人的控制过程中，机器人导航是移动机器人研究的一个重点领域，其中路径规划的研究更是机器人导航能力的一个重要体现[1]。

移动机器人的路径规划主要目标是使得机器人在从起始点到目标点运动的过程中避免出现碰撞，因此需要寻找一条最优的路径实现机器人在移动过程中的无碰撞运动[2]。

国内外学者作了大量的研究并提出了很多方法，目前移动机器人的路径规划方法主要有全局路径规划和局部路径规划[3-4],其根据传感器获取的信息寻找躲避障碍物的最优路径，并根据传感器信息实时调整路径寻优的策略。可视图算法[5]根据图搜索的完备性理论可以实现最优路径搜索，但是该算法由于计算量大，收敛速度慢，寻优的能力较差，在实时性和可靠性高的要求中无法满足需求[6]。随着遗传算法和神经网络算法的深入研究，很多学者将这些启发式的路径规划算法引入到了机器人的路径规划中实现局部路径规划[7]；但这些算法大多存在局部最优的问题，因此为了解决这一问题需要不断地引入新的算法实现路径的最优规划，与此同时增加了算法的复杂度[8]。粒子群优化(Particle Swarm Optimization, PSO)算法[9]具有计算简单、全局寻优能力强、收敛速度快等优点，在各类多维连续空间优化问题上取得了非常好的效果。许多学者对粒子群优化算法在路径规划领域的应用展开了研究。

文献[10]首次将PSO算法引入移动机器人路径规划中，该算法首先采用链接图建立机器人工作空间模型，用Dijkstra 算法求得链接图最短路径,然后用PSO算法对此路径进行优化，得到全局最优路径；但是由于链接图并不能完全体现实际规划环境中的信息，二次优化后得到的路径不一定是全局最优路径, 因此该方法限制了PSO算法的全局寻优能力。文献[11]利用三次Ferguson样条算法对移动机器人路径规划进行描述，将路径规划问题转化为三次样条的参数优化问题，为PSO算法在机器人路径规划中的应用提供了新的思路；但是，由于PSO算法普遍存在早熟收敛问题使得规划结果容易陷入局部极值。文献[12]针对三次样条早熟收敛问题，提出了具有速度变异的PSO算法，从而改善了早熟收敛问题。针对PSO算法在移动机器人的全局路径规划过程中容易出现由于过早收敛导致算法陷入局部最优的问题，文献[13]提出了一种带扰动机制的PSO算法。当算法在搜索最优解的过程中陷入局部最优时，采用粒子修正方法产生新的粒子替代原来的粒子，以此来引导算法摆脱局部最优值，搜索可行路径。为了充分利用PSO算法的全局寻优能力，文献[14]采用罚函数法表示粒子适应度函数，解决过早收敛的问题；并且为了缩短算法的执行时间，在执行过程中加入碰撞能量测试点，但没有给出碰撞和距离能量函数的权重比，因此最佳路径的寻优无法保证。

针对当前移动机器人路径规划中的算法收敛速度慢和局部最优的问题，本文将斥力势场引入PSO算法，首先采用栅格法对机器人的移动路径进行初步规划，并将栅格法得到的初步路径作为粒子的初始种群；然后根据粒子之间的相互协作实现对粒子的位置和速度的不断更新；最后采用障碍物斥力势场构造高安全性适应度函数，从而得到一条机器人从开始位置到目标的最优路径。

1 栅格法实现路径规划的数学建模

1.1 栅格法表示机器人工作空间

栅格法将机器人的工作空间表示成一个二维区域，该二维区域进行栅格划分，分解成一系列的以基本元素为单元的最小栅格，在二维区域的自由区域基本元素取值为0，在图1中用白色表示；障碍物区域取值为1，在图中用灰色表示，如图1所示为机器人工作空间的栅格法表示。

设机器人在平面上运动的二维区域为AS，原点坐标为(0,0)，任意栅格表示为g(x,y)∈AS，其中x表示该栅格所在的行号，y表示该栅格所在的列号；S={1,2,…,n}表示所有栅格的集合。x和y方向的最大值分别为xmax和ymax，机器人行走的步长为δ，则机器人工作空间中的每行和每列的栅格数分别为Nx=xmax/δ和Ny=ymax/δ。对于任意的栅格g(xi,yi)与栅格序号集合互为映射关系，则第i个栅格可表示为：

(1)

其中：mod为模运算，int为向下取整运算。

1.2 确定栅格

由图1可见，当划分的栅格粒度越小时，障碍物的表示越精确，但是工作空间划分得越细所占用的存储空间会越大，同时会导致算法的复杂度增加；如果选择的栅格粒度太大又容易造成路径规划不准确。因此在栅格法的初步规划中，粒度大小的选择是栅格法面临的主要问题。

在得到机器人工作空间的地图之后，首先根据障碍物的不同的形状进行剖分，其中椭圆和不规则图形按照能覆盖的最小长方形计算，凸多边形则进行三角剖分，根据剖分的结果计算地图中障碍物所占的总面积；然后根据障碍物所占的整个地图的总面积的比例来决定栅格的粒度大小。栅格粒度大小的计算方法如下：

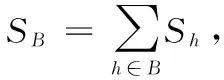
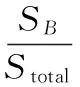
(2)

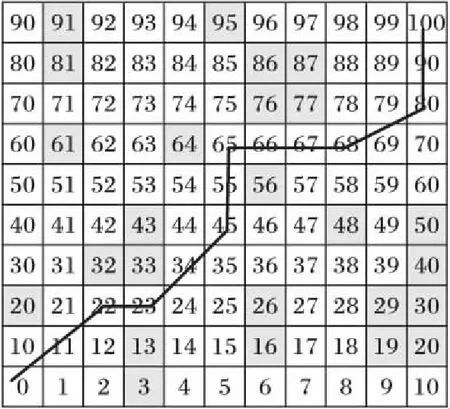
图1 机器人工作空间栅格法表示Fig. 1 Robot working space represented by grid method

1.3 路径规划数学建模

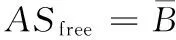
在XOY地图上建立以为p0为原点，pend为终点的新的X′轴，与之垂直的为Y′轴，则原坐标系中的点在新坐标系中的表示为：

(3)

其中α为X坐标轴与X′的夹角。

将p0pend线段作m+1垂直等分处理，将pend写为pm+1，其中与X′垂直的平行线簇(l1,l2,…,lm)与X′的交点的序列(p1,p2,…,pm)即为路径的序列，如图2所示。

规划路径的长度LP为：

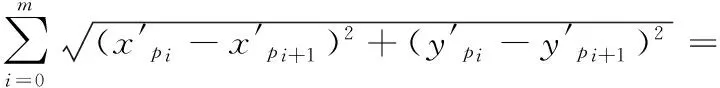
(4)

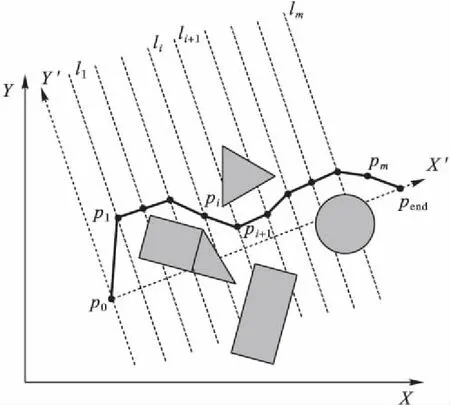
图2 路径规划坐标变换Fig. 2 Path planning coordinate transformation

2 改进的PSO算法实现路径优化

2.1 粒子速度与位置更新

PSO算法是模拟鸟类觅食行为的速度-位置搜索模型，其粒子的优劣程度由粒子的适应度函数f(x)决定，而且每一个粒子在运行的过程根据自身的个体极值Pbest和整个种群目前最优解的全局极值Gbest来更新位置和速度，以在搜索空间中向更好的位置运动，从而搜索全局最优解[14]。

在1.3节介绍的路径规划方法中采用垂直等分的形式按照式(4)进行处理，所以采用PSO算法时的粒子维数为m，而垂线li上点的Y′坐标则构成粒子的位置编码。

由图2可见可将粒子定义为由起始点p0经过不同的连接线到达终点pend的距离，即每一个粒子代表一段距离。粒子的适应度函数即为路径长度表达式(4)，因此当适应度函数的值越小则得到的解即为最优解。

在m维空间中，第i个粒子的位置可表示为向量Xi=(xi1,xi2,…,xim)，通过向量Xi可以确定每个粒子点在链接线上的坐标，计算相邻两点之间的距离，从而计算适应度值。根据适应度值的大小决定当前的解是否为局部最优，如果是则替换历史局部最优Pbest。

局部最优Pbest的适应值随着迭代的进行不断进行更新;而全局最优Gbest则是与各个Pbest进行比较，如果局部最优Pbest的适应值小于全局最优Gbest则更新全局最优的值为该Pbest的值。

为了得到移动机器人的全局最优路径，需要在计算过程中不断更新粒子的速度和位置，其中粒子i表示为向量Xi=(xi1,xi2,…,xim)，粒子的飞行速度为Vi=(νi1,νi2…,νim)。则粒子的速度和位置更新公式如下：

(5)

其中：vi, j(t+1)和xi, j(t)分别表示t时刻第i个粒子在j维的速度和位置；ω为惯性权重因子，ω取值越大则算法具有较高的全局搜索能力，反之则具有较强的局部搜索能力。惯性权重ω随着迭代次数的增加线性减少，可以使粒子种群在开始时进行大范围的最优解空间的搜索，然后随着迭代次数的增加逐渐缩小搜索范围，从而加强搜索现有解空间的能力。因此本文设计惯性权重ω的取值方法如下：

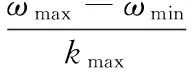
其中：ω的最大值和最小值在本文的实验中取ωmax=0.9，ωmin=0.4；ki为当前的迭代次数，kmax为最大迭代次数。

c1、c2分别为个体和全局的加速因子，即每个粒子受到个体极值Pbest和全局极值Gbest位置吸引的加速度的权重。加速因子使得每个粒子都具有自我总结并向群体中其他优秀个体学习的能力，从而使粒子在前进的过程中向自己的历史最优点以及群体内的全局最优点靠近。其中c1调节粒子飞向自身最好位置方向的步长，c2调节粒子飞向全局最好位置方向的步长。r1、r2为随机数，一般取[0,1]。Pi, j(t)和Gj(t)分别表示到t时刻为止第i个粒子在j维分量搜索到的个体最优位置以及整个种群粒子的第j维分量搜索到的最优位置。

2.2 构造高安全性适应度函数

将人工势场原理引入到适应度函数的构建中，使移动机器人在人工势场中移动时，同时受到目标位置的引力场的引力和障碍物的斥力场的斥力两种力的共同作用。由于斥力场与障碍物有关，因此，机器人在运动的过程中距离障碍物越近则产生的斥力就越大，同时机器人碰触障碍物的危险系数越高。由于引力场的作用与机器人的运动目标位置有关，因此从算法的复杂度考虑，本文构建高安全性适应度函数时只考虑斥力场的作用。

障碍物附近的斥力场函数表示为：

(6)

其中：η为障碍物的斥力系数；p为机器人在空间中移动时的任意位置，ρ(p)为移动机器人到障碍物的最短距离；ρ0为障碍物的斥力场的作用距离。

为了保证在整个势力场中只有在目标点位置时全局最小，因此在式(6)的基础上引入机器人与目标点的相对位置，即在原有的基础上乘以一个距离因子:

Urep=

(7)

斥力为斥力势函数的负梯度，则可得斥力为：

Frep=-grad(Urep)=

(8)

机器人在移动过程中由于路径点的安全性不仅与障碍物的远近有关，还与空间中障碍物的分布密集程度有关，因此由式(8)可得，移动机器人在空间中的任意位置xi, j处的安全度为：

safei, j=

(9)

其中：s为模板窗口尺寸因子，并且窗口的实际尺寸为(2s+1)2，当s减小时，窗口中会包含较少的障碍物信息，此时安全系数safei, j增大；sign(m,n)为点xi+m, j+n处的障碍物标志，当xi+m, j+n点为障碍物时sign(m,n)=1，否则，sign(m,n)=0。因此可由式(9)计算出机器人在移动的过程中所处位置的安全性系数。

则由式(9)可得路径Ppath的安全度为：

(10)

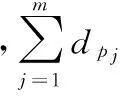
由式(4)和式(10)可得路径Ppath的优化函数为：

fP=ω1LP+ω2MP

(11)

通过调整加权因子ω1和ω2来调整LP和MP在路径规划中所占的比重，从而选择路径和安全性均适中的路线。

2.3 路径优化算法实现

设定义n个m维粒子，采用式(11)作为第i个粒子的适应度函数：

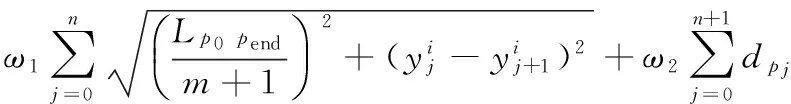
(12)

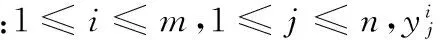
利用适应度函数对所得的路径集合进行优化, 从而求解全局最优路径，适应度函数得到的值越小，所得的解越优。

算法实现的具体步骤如下：

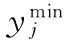
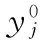
(13)

由式(5)得到粒子的第i个粒子第j维的初始速度和位置为：

(14)

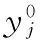
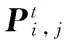
步骤5 对每个粒子按照式(5)中的位置和式(6)的速度进行更新，注意粒子两端和边界的约束。

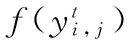
步骤7 如果达到了最大迭代次数或者是最小精度要求，则输出最优路径，否则转到步骤4继续执行。

算法流程如图3所示。

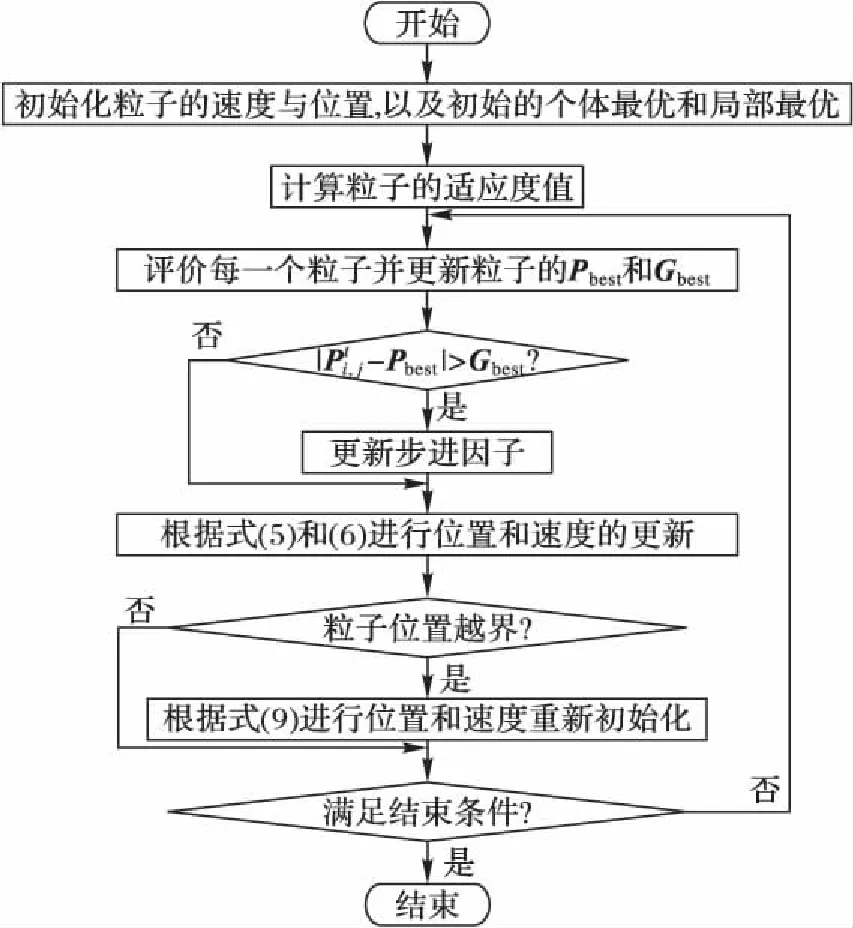
图3 本文算法流程Fig. 3 Flow chart of the proposed algorithm

3 仿真与分析

为了验证算法的有效性，以Visual studio 2010为平台，C# 语言为编程环境进行仿真。实验的硬件平台为：Intel Core i5 3.20 GHz CPU；4 GB内存；500 GB硬盘，Windows 10操作系统。

为了验证本文算法的有效性，在相同的环境模型下将本文方法与线性递减惯性权重粒子群优化算法(Linearly Decreasing Weight Particle Swarm Optimization, LDWPSO)[13]进行对比实验。

3.1 最优路径与收敛性比较

采用1.2节的方法确定栅格，经过多次对不同实验环境(包括本文的实验环境1、2以及图8所示环境)的测试，取lmax=20，lmin=3时栅格粒度较适合实验目的。实验环境1和2相对障碍物较少，因此栅格粒度较大；而图8中的实验环境下障碍物较密，因此栅格粒度较小。

实验环境1参数描述：实验环境采用15×15方格的环境，环境中障碍物数目为42，每一个方格表示一个障碍物。移动机器人运动起点为(0,0)，终点位置为(14,14)。

如图4所示为本文算法与LDWPSO的最优解对比结果。LDWPSO算法在第32次迭代时找到了最优解，本文算法则是在第25次迭代时已经找到了符合终止条件的最优解。因此从算法的收敛性上来看本文算法优于LDWPSO算法，并且寻找的最优路径的栅格长度本文算法为17，LDWPSO算法为19。

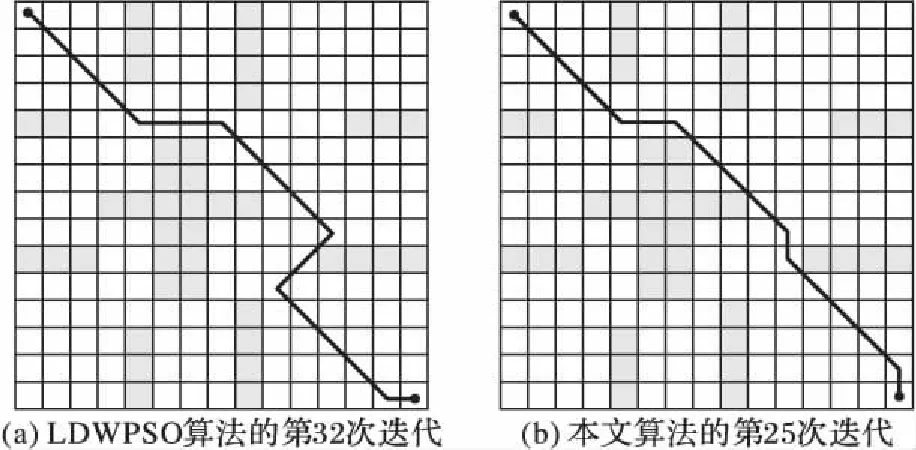
图4 环境1最优路径对比Fig. 4 Comparison of optimal path in environment 1

图5给出了本文算法的避障过程，在由第17次向第18次迭代的过程中，能够明显地躲避障碍，并且在搜索的过程中搜索范围较大，能够跳出局部最优。

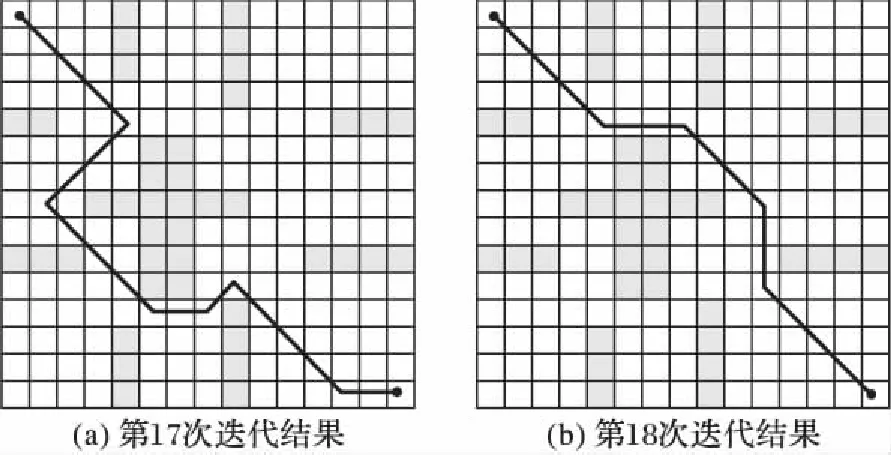
图5 本文算法的第17次迭代和第18次迭代的避障情况Fig. 5 Obstacle avoidance of 17th and 18th iterations by the proposed algorithm

实验环境2参数描述：实验环境采用10×10方格的环境，环境中障碍物数目为31，每一个方格表示一个障碍物，并且分布无序；移动机器人的起始位置为(0,0)，终点位置为(9,9)。

由图6可以看出本文算法克服了局部最优的缺陷并成功搜索到了最优路径，本文算法搜索路径的栅格长度为12，而LDWPSO算法则为14。

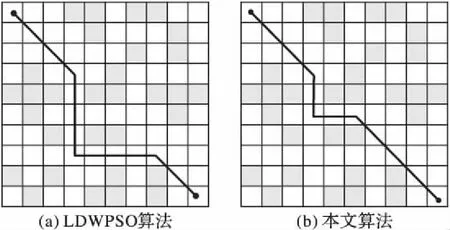
图6 环境2最优路径对比Fig. 6 Comparison of optimal path in environment 2

图7给出了两种算法的收敛性比较，可以看出：本文算法在50次的迭代过程中都在第6次找到了局部最优解，第12次迭代之后找到了最优解，并稳定在最优解；而LDWPSO算法则在第17次达到了局部最优并且没有跳出局部最优解。因此从算法的收敛性和克服局部最优解方面本文算法优于LDWPSO算法。

3.2 本文算法不同实验环境最优路径对比

在本实验中采用相同的实验地图，但是实验环境中的障碍物数目、位置以及状态不同。实验结果如图8所示，由图可以看出对于不同的实验环境，本文算法都能得到最优的路径规划，说明本文算法对于复杂环境具有较高的适应性。

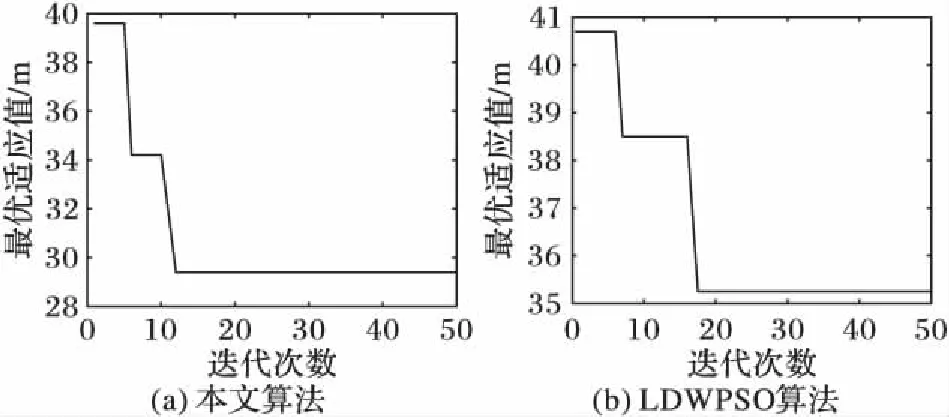
图7 两种算法收敛性比较Fig. 7 Convergence comparison of two algorithms

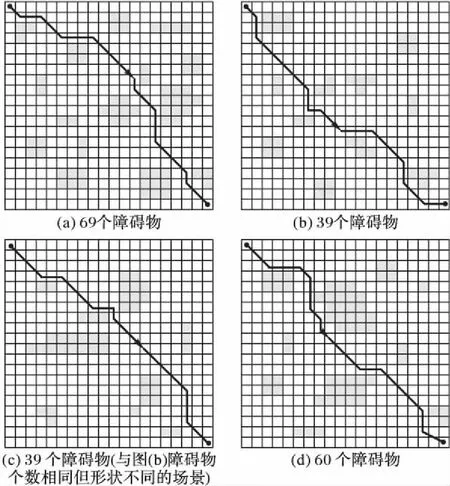
图8 不同环境的最优路径规划Fig. 8 Optimal path planning in different environments

4 结语

本文针对传统的粒子群优化(PSO)算法实现移动机器人路径规划中的局部极值问题以及适应度函数在计算过程中的粒子安全性问题，提出了斥力势场下粒子群优化的移动机器人路径规划算法，该算法为移动机器人在复杂环境下的路径规划提供了一种有效的选择。该算法主要有以下特点：1)该算法利用栅格法实现机器人路径的初步规划，并将初始规划的路径作为粒子的初始种群；2)根据粒子之间的相互协作实现对粒子的位置和速度的不断更新，解决路径规划中的局部极值问题；3)采用障碍物斥力势场构造高安全性适应度函数。通过实验仿真验证本文算法能获得路径寻优的最优解，并且算法的收敛速度快。

References)

[1] 朱大奇,颜明重.移动机器人路径规划技术综述 [J].控制与决策,2010,25(7):961-967. (ZHU D Q, YAN M Z. Survey on technology of mobile robot path planning [J]. Control and Decision, 2010, 25(7): 961-967.)

[2] 蔡自兴,贺汉根,陈虹.未知环境中移动机器人导航控制理论与方法[M]. 北京：科学出版社,2009:8-12. (CAI Z X, HE H G, CHEN H, Mobile robot navigation in unknown environment control theory and method [M]. Beijing: Science Press,2009:8-12.)

[3] CLERC M, KENNEDY J. The particle swarm-explosion, stability and convergence in a multidimensional complex space [J]. IEEE Transactions on Evolutionary Computer, 2002, 6(1): 58-73.

[4] SHI P, HUA J N. Mobile Robot dynamic path planning based on artificial potential field approach [J]. Advanced Materials Research, 2012, 490-495: 994-998．

[5] SUD A, ANDERSEN E, CURTIS S, et al. Real-time path planning in dynamic virtual environments using multiagent navigation graphs [J]. IEEE Transactions on Visualization and Computer Graphics, 2008, 4(3): 526-538.

[6] TAVARES R S, MARTINS T C, TSUZUKI M S G. Simulated annealing with adaptive neighborhood: a case study in off-line robot path planning [J]. Expert Systems with Applications, 2011, 38(4): 2951-2965.

[7] GHATEE M, MOHADES A. Motion planning in order to optimize the length and clearance applying a Hopfield neural network [J]. Expert Systems with Applications, 2009, 36(3): 4688-4695.

[8] 杜宗宗,刘国栋.基于遗传模拟退火算法的移动机器人路径规划[J].计算机仿真,2009,26(12):118-121. (DU Z Z, LIU G D. Path planning of mobile robot based on genetically simulated annealing algorithm[J]. Computer Simulation, 2009, 26(12): 118-121.)

[9] ZENG N, ZHANG H, CHEN Y, et al. Path planning for intelligent robot based on switching local evolutionary PSO algorithm [J]. Assembly Automation, 2016, 36(2): 120-126.

[10] 秦元庆,孙德宝,李宁，等.基于粒子群算法的移动机器人路径规划[J].机器人,2014,26(3):222-225. (QIN Y Q, SUN D B, LI N, et al. Path planning for mobile robot based on particle swarm optimization [J]. Robot, 2014, 26(3): 222-225.)

[11] SHENG J W, HE G H, GUO W B et al. An improved artificial potential field algorithm for virtual human path planning [C]// Proceedings of the 2010 International Conference on Entertainment for Education Digital Techniques & Systems, LNCS 6249. Berlin: Springer-Verlag, 2010: 592-601

[12] SETHANAN K, NEUNGMATCHA W. Multi-objective particle swarm optimization for mechanical harvester route planning of sugarcane field operations [J]. European Journal of Operational Research, 2016, 252(3): 969-984.

[13] TANG Z, ZHOU Y. A glowworm swarm optimization algorithm for uninhabited combat air vehicle path planning [J]. Journal of Intelligent Systems, 2014, 24(1): 69-83.

[14] TANG B, ZHU Z, LUO J. A convergence-guaranteed particle swarm optimization method for mobile robot global path planning [J]. Assembly Automation, 2017, 37(1): 114-129.

This work is partially supported by the Science and Technology Plan Projects of Hebei Province (15220327, 16222101D- 2), the Youth Topnotch Talent Program of Hebei Universities and Colleges (BJ2017105).

HANMing, born in 1984, Ph. D., lecturer. His research interests include intelligence robot, pattern recognition and control.

LIUJiaomin, born in 1958, Ph. D., professor. His research interests include intelligence control, pattern recognition.

WUShuomei, born in 1977, M. S., lecturer. Her research interests include pattern recognition, machine vision.

WANGJingtao, born in 1984, M. S., assistant. Her research interests include intelligence computing, pattern recognition.

Pathplanningalgorithmofmobilerobotbasedonparticleswarmoptimization

HAN Ming1,2*, LIU Jiaomin2, WU Shuomei1, WANG Jingtao1

(1.CollegeofComputerScienceandEngineering,ShijiazhuangUniversity,ShijiazhuangHebei050035,China；2.SchoolofInformationScienceandEngineering,YanshanUniversity,QinhuangdaoHebei066004,China)

Concerning the slow convergence and local optimum of the traditional robot path planning algorithms in complicated enviroment, a new path planning algorithm for mobile robots based on Particle Swarm Optimization (PSO)algorithm in repulsion potential field was proposed. Firstly, the grid method was used to give a preliminary path planning of robot, which was regarded as the initial particle population. The size of grids was determined by the obstacles of different shapes and sizes and the total area of obstacles in the map, then mathematical modeling of the planning path was completed. Secondly, the particle position and speed were constantly updated through the cooperation between particles. Finally, the high-security fitness function was constructed using the repulsion potential field of obstacles to obtain an optimal path from starting point to target of robot. Simulation experiment was carried out with Matlab. The experimental results show that the proposed algorithm can implement path optimization and safely avoid obstacles in a complex environment; the contrast experimental results indicat that the proposed algorithm converges fast and can solve the local optimum problem.

grid method; Particle Swarm Optimization (PSO); path planning; progress factor; fitness function

TP391; TP18

A

2017- 01- 17;

2017- 03- 05。

河北省科技计划项目(15220327, 16222101D- 2)；河北省高等学校青年拔尖人才计划项目(BJ2017105)。

韩明(1984—)，男，河北行唐人，讲师，博士，CCF会员，主要研究方向：智能机器人、模式识别与控制； 刘教民(1958—)，男，河南西峡人，教授，博士生导师，博士，CCF会员，主要研究方向：智能控制、模式识别； 吴朔媚(1977—)，女，河北邢台人，讲师，硕士，主要研究方向：模式识别、机器视觉； 王敬涛(1984—)，女，河北邯郸人，助教，硕士，主要研究方向：智能计算、模式识别。

1001- 9081(2017)08- 2258- 06

10.11772/j.issn.1001- 9081.2017.08.2258