基于趋势特征表示的shapelet分类方法
2017-10-21闫欣鸣孟凡荣闫秋艳
闫欣鸣,孟凡荣,闫秋艳
(中国矿业大学 计算机科学与技术学院,江苏 徐州 221116)
(*通信作者电子邮箱yanxm@cumt.edu.cn)
基于趋势特征表示的shapelet分类方法
闫欣鸣*,孟凡荣,闫秋艳
(中国矿业大学 计算机科学与技术学院,江苏 徐州 221116)
(*通信作者电子邮箱yanxm@cumt.edu.cn)
Shapelet是一种具有辨识性的时间序列子序列,通过识别局部特征达到对时间序列准确分类的目的。原始shapelet发现算法效率较低,大量工作关注于提高shapelet发现的效率。然而,对于带有趋势变化的时间序列,采用典型的时间序列表示方法进行shapelet发现,容易造成序列中趋势信息的丢失。为了解决时间序列趋势信息丢失的问题,提出一种基于趋势特征的多样化top-kshapelet分类方法:首先采用趋势特征符号化方法对时间序列的趋势信息进行表示;然后针对序列的趋势特征符号获取shapelet候选集合;最后通过引入多样化top-k查询算法从候选集中选取k个最具代表性的shapelets。在时间序列的分类实验中,与传统分类算法相比,所提方法在11个数据集上的分类准确率均有提升;与FastShapelet算法相比,提升了运行效率,缩短了算法的运行时间,并在趋势信息明显的数据上效果显著。结果表明,所提方法能有效提高时间序列的分类准确率,提升算法运行效率。
shapelet;趋势特征;符号化;多样化top-k查询; 时间序列分类
0 引言
近些年来,人们对于时间序列数据挖掘的兴趣越来越浓厚。其中大多数的研究是基于不同距离度量方法的最近邻算法,如欧氏距离、动态时间归整(Dynamic Time Warping,DTW)等。2009年,Keogh等提出了shapelet的概念[1],引起了广泛的关注,并在时间序列的分类[2]和聚类[3]等领域有了广泛的应用。通俗来讲,shapelet是时间序列的子序列,是时间序列中具有辨识度的局部特征,它在某种意义上能够最大限度地代表一个类,并据此很好地区分两类间的不同[4]。原始的shapelet分类方法是利用shapelet构造决策树,这种分类方法相比最近邻算法(Nearest Neighbor Algorithm, 1NN)有较大提高,然而它并不能胜任多分类问题。2012年,Lines等在文献[5]中利用shapelet对原始数据集进行转换,使用这种方法,能够对原始的时间序列降维,并将shapelet发现与构造分类器分离开来,而后利用转换后的数据与其他分类器结合使用,从而克服了原始shapelet方法在多分类问题上的不足。2014年,原继东等在文献[6]中提出了基于shapelet的剪枝和覆盖算法,对降低shapelet集合的冗余性作出了改进。
由于时间序列通常是连续的高维数据,许多研究者采用时间序列符号化方法对时间序列进行离散化、降维[7]。2007年,Lin等在文献[8]中提出了符号聚集近似(Symbolic Aggregate approXimation,SAX)算法,SAX因其简易高效的特性而广受欢迎。2013年,Keogh等在文献[9]中提出了快速shapelet算法,通过将时间序列进行SAX符号化表示,利用生物信息学中的随机规划[10]算法评判shapelet的分值,大大提高了shapelet发现的效率。
然而,现实生活中带有趋势变化的时间序列挖掘对我们提出了新的挑战,例如:股票数据、天气数据、居民用电量等,此类数据中的趋势信息对于发现特殊事件的发展规律和对异常事件预测预警,具有重要意义。典型的时间序列符号化表示方法,如分段聚集近似(Piecewise Aggregate Approximation, PAA),SAX等,均使用平均值对序列的分段特征进行表示,对于时间序列的趋势特征,如上升(下降)、角度、幅度等信息,则无能为力。
为了解决现有shapelet分类方法无法有效表示时间序列趋势特征的问题,本文提出了一种基于趋势特征的多样化top-kshapelet分类方法,该方法首先采用趋势特征符号化方法对时间序列的趋势信息进行表示;然后针对序列的趋势特征符号获取shapelet候选集合;最后通过引入多样化top-k查询算法[11]从候选集中选取k个最具代表性的shapelets[12]。实验部分分别选取公测数据和实际数据,将本文方法与对比算法进行比较,结果表明本文算法针对具有趋势特征的时间序列数据具有更好的分类效果。
1 相关定义
表1总结了本文涉及的相关符号,并于下文对其进行了详细释义。

表1 符号表Tab.1 Symbol table
定义1 时间序列。时间序列T=t1,t2,…,tm是一段时间等间隔的实值序列,m是时间序列的长度。
定义2 子序列。一条时间序列的子序列S=tp,tp+1,…,tp+l-1是T上一段连续的序列,p是开始位置,l代表长度。
定义3 时间序列间的距离。对于两条时间序列T和Q,定义T和Q之间的距离为:

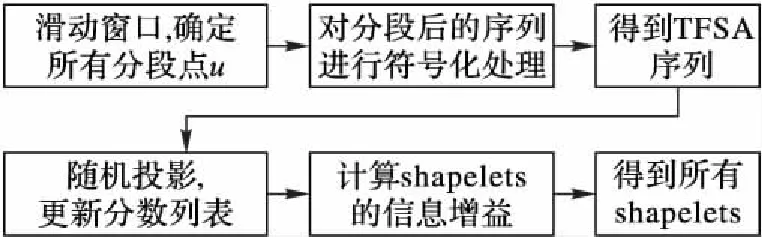
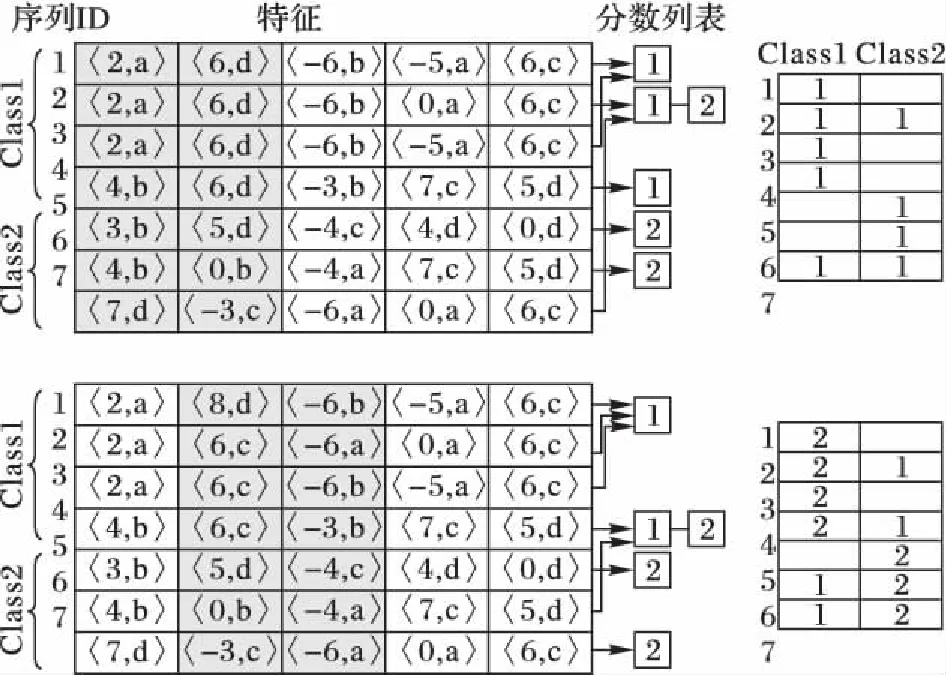
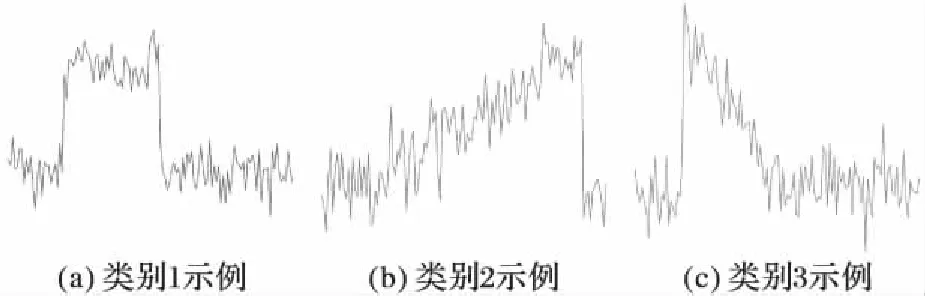
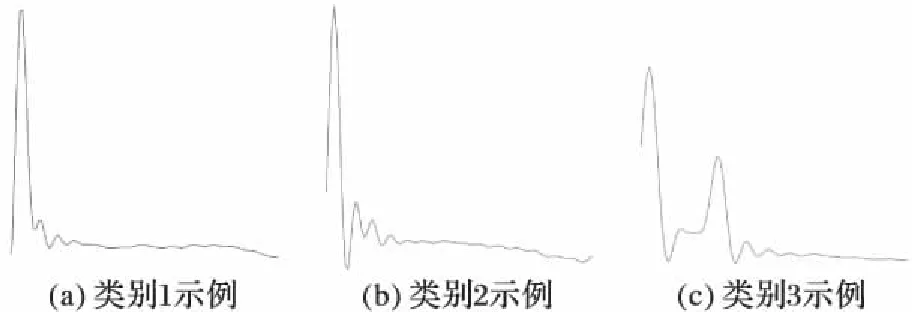
定义5 分裂点[1]。分裂点〈S,d〉是一个二元组,其中S为时间序列子序列,d为距离阈值。分裂点表示存在某一距离阈值d使得数据集D被其分为两个数据集DL和DR,并且对于所有的TL和TR都有SubseqDist(S,TL) 定义6 信息增益。一个分裂点〈S,d〉的信息增益为: 其中E(D)表示数据集D的熵,计算公式如下: E(D)=-∑p(Ci) lb (p(Ci)) 定义7 shapelet[1]。是一个最优分裂点,采用信息增益作为量度,能够将数据集D一分为二,并且使得最终的信息增益最大,即满足IG(〈shapelet,dosp〉)≥IG(〈S,d〉),其中IG为该分裂点的信息增益。 定义8 shapelet相似[6]。对于任意两个shapelet 〈S1,d1〉和〈S2,d2〉,若SubseqDist(S1,S2) 定义9 多样化top-k查询[11]。给定一个查找集合I={v1,v2,…}和一个正整数k,其中对于任意vi∈I,vi的分数可以表示为score(vi),并且1≤k≤|I|。定义多样化top-k查询结果D(I)满足以下条件: 1)D(I)⊆I并且|D(I)|≤k; 2)对于任意两个结果vi∈I和vj∈I,并且vi≠vj,如果vi与vj相似,那么vi和vj不同属于D(I); 定义10 多样化图[11]。给定一个查找集合I={v1,v2,…},其多样化图表示为无向图G(I)=(V,E),其中V是I中所有变量组成的顶点集合,若vi与vj相似,则两点间有一条边,记为E。为了不失一般性,假定G(I)中的点都是以其分数非递增排列的,即1≤i 定义11 多样化top-kshapelets[12]。在候选shapelets集合I={S1,S2,…,Sn}中,满足下列条件的k个shapelets,将其表示为DivTopk(I): 1)DivTopk(I)⊆I,|DivTopk(I)|≤k; 2)对于任意两个shapelets,Si,Sj∈I,Si≠Sj,如果Si和Sj相似,则Si和Sj不同属于DivTopk(I); 本文给出一种基于趋势特征的多样化top-kshapelet分类方法(Trend-based Diversified top-kShapelet, TDTS),算法主要分为三个部分:1)对序列进行趋势特征符号化,并进行shapelets发现;2)对产生的shapelets候选集进行多样化top-k查询,选出k个最具代表性的shapelets;3)使用shapelet转换技术对原始数据集进行转换,并利用转换后的数据集进行分类。算法伪代码见算法1。 算法1 TDTS。 输入 数据集D; 输出 分类结果R。 1) allShapelets=∅ 2) allShapelets=ShapeletCandidates(D,min,max) 3) kShapelets=DivTopkSearch(allShapelets,k) 4) R=ShapeletConvert(kshapelets,D) 5) returnR 2.1 带有趋势特征的快速shapelet发现算法 本文进行shapelet发现主要利用趋势特征符号化的方法对时间序列进行降维处理,并保留序列的趋势信息,再对序列进行快速shapelet发现,以保证shapelet发现的运行效率,具体流程如图1,其中TFSA序列表示趋势特征符号化后的符号化序列,即后文中算法2的返回结果。 图1 趋势shapelet快速发现过程Fig. 1 Process of trendy shapelet quick discovery 2.1.1 时间序列的趋势特征符号化 由于时间序列大多带有趋势信息,所以在对时间序列进行符号化时需要考虑这些趋势特征。文献[9]中使用SAX对时间序列进行符号化处理,这种方法较为简洁,实现了高维到低维、实值到离散的转化。但是使用SAX方法对序列符号化并不能有效地保留时间序列的趋势信息,因此本文引入文献[13]中基于趋势特征的时间序列的符号化方法,对原始时间序列进行趋势特征符号化。 在趋势特征符号化的过程中,首先对要符号化的序列进行分段,所有分段点用u表示。分段过后,将每一段分割后的序列对应成一个二元组〈K,u〉,其中:K是该段序列的斜率,其符号代表了该段序列的趋势,正表示上升趋势,负表示下降趋势,0保持平稳;u是该段序列的终点值,即分段过程产生的分段点,最后一段序列的终点值即为整条序列的终点值。对每一段分割后的序列计算出其对应的二元组值,即完成符号化。斜率K的计算如下: (1) 其中:x表示该段序列的长度,vj表示时间戳tj在序列中对应的值。 图2给出了趋势特征符号化的一个示例。符号化方法使用滑动窗口机制计算窗口内序列的斜率,当斜率的变化(即角度angle)超过一定阈值时,产生一个分段点ui,并继续滑动窗口,以此类推。找出所有分段点后,对每一段序列进行符号化。在对每一段待符号化序列符号化的过程中,本文首先参考了文献[13]中的离散方法,将斜率值K离散地对应到集合{x|x=-9,-8, …,8,9}中,表示斜率值K在该离散值对应的区间内,例如当离散化后的斜率值K=5时,表示该段序列与x轴的夹角在(40°,50°)区间范围内;当K=-5时,表示序列与x轴夹角在(-50°,-40°)区间范围内;当K=0时,与x轴夹角为0°。而后参考了文献[8]中的符号化方法,将终点值u映射到集合{x|x=a,b,c,d}中,从而完成整个符号化过程。即将每一段序列对应成一个二元组〈K,u〉,记为q,qi表示分段后第i段序列的趋势特征符号化结果,即qi=〈Ki,ui〉,详细过程见算法2。 图2 趋势特征符号化示意图Fig. 2 Symbolization of trend feature 算法2 CreateTFSAList。 输入 数据集D,分段点个数num,阈值τ。 输出 TFSA序列集。 1) Forid=1 ton 2)U=∅ 3)l=m/num 4)S1=subseq(Tid,1,l) 5)K1=slope(S1) 6) Fori=1 tom-l 7)S2=subseq(Tid,i+1,l) 8)K2=slope(S2) 9) If |K1-K2|>τ 10)U←l+i-1 11)i=update(i) 12) >S1=subseq(Tid,i,l) 13)K1=slope(S1) 14) Else 15)K1=(K1+K2)/2 16) End For 17)TFSAList← Symbolization(U) 18) End For 19) ReturnTFSAList 算法中n表示数据集D中的时间序列个数,m表示每条时间序列的长度,Tid表示D中第id条时间序列。第一步,设置滑动窗口大小(第3)行);第二步,计算第一个窗口内序列的K1(第4)~5)行);第三步,滑动窗口,计算斜率K2,并计算两斜率的差,如果差值大于一定阈值,则认为序列趋势有变化,记一分段点ui,反之将两段序列合为一段,记K1=(K1+K2)/2,并反复执行此步骤,直至窗口滑动到序列结束,得出所有分段点(第6)~16)行);第四步,依据分段点,将每个子序列进行符号化,符号化后的信息包括序列斜率和终点值的符号化表示形式(第17)行)。最后返回已经趋势特征符号化的TFSA序列集。 2.1.2 保持趋势特征的shapelet发现算法 在对原始数据进行趋势特征符号化后,将其与原始FastShapelet算法[9]结合,在原数据的趋势符号化表示的基础上对其进行shapelet发现,具体内容见算法3。图3给出了一个基于趋势特征表示的快速shapelet发现的示例。该算法随机覆盖序列的子序列,然后对未覆盖的子序列进行Hash碰撞检测,碰撞后得出图3右侧的碰撞频次,最后通过对碰撞频次的分析(具体分析方法见文献[9]),选出候选的shapelet。由于该方法选出的shapelet在自身所在类中碰撞频次较高且在其他类中碰撞频次较低,因此该shapelet更具有代表性。 图3 趋势快速shapelet发现示意图Fig. 3 Illustration of trendy shapelet fast discovery 算法3 ShapeletCandidates。 输入 数据集D,最小长度min,最大长度max,投影次数r; 输出 Shapelet候选集allShapelets。 1)allShapelets=∅ 2) forlen=mintomax 3)TFSAList=CreateTFSAList(D,len) 4)Score={} 5) Forj=1 tor 6)Count=RandProjection(TFSAList,D) 7)Score=UpdateScore(Score,Count) 8) End For 9)KTFSACand=FindTopKTFSA(ScoreList,Score,M) 10)KShapeletCand=Remap(KTFSACand,D) 11) Fori=1 to |KShapeletCand| 12) CalInfoGain(Shapelet[i],D) 13) End For 14) All Shapelet.add(KShapeletCand) 15) End For 16) ReturnallShapelets 算法3中,首先对原始时间序列数据进行趋势特征符号化,产生指定长度的TFSA序列(具体过程见算法1),将其放入列表中(第3)行);之后,在产生的TFSA序列集上进行随机覆盖,对每一个TFSA序列产生一个碰撞频次,根据碰撞频次计算出该序列的分值(第5)~8)行);接着根据分值选取最好的M个TFSA序列,作为候选TFSA序列,并将其重新映射到原数据集上,产生候选shapelets,然后对所有候选shapelets计算信息增益,并将其加入到shapelets集合中(第9)~14)行);最后返回所有候选的shapelets。其中r是投影次数,表示算法进行了r次随机映射,本文中设r=10,M=10。 2.2 多样化top-k shapelets查询 top-k查询通常是在列表中直接按分值查询最优的k个结果,但这种方法并没有考虑到结果之间的相似性。在前文中提到的shapelets发现算法中,得到shapelets候选集,而这些shapelets间存在许多相似shapelets,由于shapelet是能够最大程度代表一个类的时间序列子序列,如果直接选取k个最优的shapelets,那么使用相似的shapelets进行分类可能使其失去了代表性。因此参考文献[11]中的多样化top-k查询,得出本文使用的多样化top-kshapelets查询[12,14],算法流程见图4,详细过程见算法4。 图4 多样化top-kshapelets查询过程 Fig. 4 Process of diversified top-kshapelets query 算法4 DivTopkSearch。 输入 shapelets候选集allShapelets,k值。 输出k个shapelets。 1)Graph=∅ 2) sort(allShapelets) 3) Fori=1 to |allShapelets| 4)Graph.add(allShapelets[i]) 5) End For 6) Forj=1 to |allShapelets| 7) Fork=1 to |allShapelets| 8) If(allShapelets[j]≈allShapelets[k]) 9)Graph[j].add(Graph[k]) 10)Graph[k].add(Graph[j]) 11) End For 12) End For 13)kShapelets=∅,n=|V(Graph)| 14)kShapelets.add(v1) 15) while(|kShapelets| 16) Fori=2 ton 17) If(vi.adj(Graph)∩kShapelets=∅) 18)kShapelets.add(vi) 19) End If 20) End For 21) returnkShapelets 算法由两部分构成。第一部分,构造多样化shapelets图(第1)~12)行)。首先对算法1中得到的所有shapelets根据其信息增益进行排序,并将其作为点加入图中(第1)~5)行);接着依次遍历所有shapelets,判断与其他shapelets是否相似,如若相似,在两点间构造一条边(第6)~12)行)。这样便完成了多样化shapelets图的构造。第二部分,查询多元化top-kshapelets(第13)~21)行)。首先将信息增益最大的shapelet(v1)放到kShapelets集合中(第14)行)。如果k=1,此时算法将会结束,并返回该shapelet;否则,对于多元化图中的其他节点,如果该节点的邻接节点都不在kShapelets中,就可以将该节点加入到kShapelets中(第15)~20)行)。最后返回k个多元化shapelets(第21)行)。 2.3 shapelet转换分类方法 在得到所有shapelets候选集后,采用shapelet转换技术对原始数据集进行转换[5]。转换过程中计算时间序列与所有shapelets的距离,记为新的一条时间序列。将传统的分类方法应用于转换后的数据集进行分类,得出分类结果。 2.4 算法时间复杂度分析 算法首先进行时间序列的趋势特征符号化,其时间复杂度为O(nm),其中n表示时间序列的个数,m表示时间序列的长度;而后使用快速shapelet发现算法进行shapelet发现,其时间复杂度为O(nm2);而多样化Top-kshapelets查询的时间复杂度为O(p2),p为候选shapelets个数。因此,算法总体时间复杂度为O(nm2)+O(p2)。 3.1 实验说明 通过对算法的设计与实现,现利用算法对合适的数据集进行分类以验证其效果,数据集的选取将在3.2节详细介绍。算法首先通过与原始时间序列分类方法对比,以验证shapelet分类的有效性;而后对比本文算法与FastShapelet算法的效果,以验证趋势特征符号化在提高分类准确度上的有效性。由于算法需要选取k个shapelets参与最后的分类,实验过程中需要对k值进行设定,k值的选取见3.3节。在3.4节给出了本文算法与对比算法的分类准确率对比,以验证本文算法的效果。在3.5节对则本文算法与FastShapelet算法的运行时间进行了对比。 3.2 数据集的选取 实验选取了多种数据集进行测量。第一种采用UCR数据集[15],选取其中7个数据集做了进一步的实验;第二种使用千秋矿上电磁辐射的强度和脉冲数据,以其状态异常或正常进行分类;第三种选用加州大学欧文(尔湾)分校机器学习库中的占用检测(Occupancy Detection)数据集[16],实验数据采集温度、湿度、灯光和二氧化碳浓度等,对办公室占用或者不占用进行二分类。 在这些数据集当中,有一部分时间序列有着明显的趋势特征,例如UCR数据集中的CBF数据集,示例如图5所示;而另一部分则不明显具有趋势特征,例如UCR数据集中的MedicalImages数据集,由于该数据集类别过多,此处仅列举3类示意,示例如图6所示。可以看出本文算法在包含有明显趋势特征的数据集上有着良好的效果。 图5 CBF数据集部分序列示例Fig. 5 Illustration of part series in CBF dataset 图6 MedicalImages数据集部分序列示例Fig. 6 Illustration of part series in MedicalImages dataset 3.3k值选取说明 算法中k取值的不同会对算法的结果造成影响,因此k值的选取相当关键。针对不同k值对本文算法进行测试的结果如图7所示,可以看出,随着k取值的增加,算法的结果趋于稳定,当k大于13以后,算法的结果稳定在某一数值,因此在以后的对比实验中,均取k=13时的算法分类准确度作为对比实验的比对数据。 3.4 分类准确率对比 为了说明本文所提出的TDTS算法能够提高包含有趋势特征的时间序列的分类准确率,将其与其他算法在多个数据集上的分类准确度进行对比。算法将原始数据集进行shapelet转换,并将转换后的结果运用于多个原始分类器上以评估算法的效果。表2展现了TDTS算法与传统分类算法的准确率对比,对比算法包括C4.5、1NN、朴素贝叶斯(Naive Bayes, NB)、贝叶斯网络(Bayesian Network, BN)、随机森林(Random Forest, RanF)、旋转森林(Rotation Forest, RoF)、支持向量机(Support Vector Machine, SVM)。表2中:第1列为测试数据集,第2列为单独C4.5算法对各数据集分类的准确率(以“单独”表示),第3列为C4.5算法应用于本文算法后得出的分类准确率(以“结合”表示),以此类推,最后一行表示TDTS算法对比传统分类算法分类准确率有所提升的数据集个数。对比结果表明,在11个数据集上,TDTS算法对大部分数据集在准确率上均有所提升。 由于FastShapelet算法采用SAX符号化方法对原始时间序列符号化,本文算法思路与其相似,为了体现TDTS更能保留时间序列的趋势特征,选取FastShapelet算法作为本文的对比算法。表2展示了FastShapelet算法在不同数据集上的分类准确率,图8对TDTS算法与FastShapelet算法在分类准确率上进行了对比。对比显示,本文算法在11个数据集上有7个数据集要好于FastShapelet,表明本文算法能够较好地提高分类准确率。 图7 不同数据集分类准确率随k变化过程Fig. 7 Classification accuracy of different datasets changing with k 图8 TDTS与FastShapelet分类准确率对比Fig. 8 Classification accuracy comparison between TDTS and FastShapelet algorithms 3.5 shapelet发现时间对比 由于算法在shapelet发现阶段耗时最长,本文仅对比算法在shapelet发现阶段所用时间,结果如表4所示,其中加速倍数=FastShapelet算法运行时间/TDTS算法运行时间。由于本文算法在进行shapelet发现前先对时间序列整体进行符号化,而原始FastShapelet算法则是在shapelet发现过程中对子序列进行符号化进而计算shapelet,因此本文算法在运行时间上要少于原始FastShapelet算法。由表4可以看出,与FastShapelet算法相比,TDTS算法一定程度上提升了时间效率。本文算法采用先符号化后进行shapelet发现的过程,与FastShapelet算法相比,本文算法主要节省了符号化的时间,但由于本文符号化的结果是一个个二元组,在处理符号化后序列的过程中会比FastShapelet算法慢。MoteStrain等数据集原始序列长度较短,造成本文算法运行时间比FastShapelet算法长,先处理符号化后进行shapelet发现的优势无法体现,因此无法加速;而FaceFour等数据集原始序列长度较长,更能体现本文算法优势。由于时间序列大多较长,因此可以认为本文算法在提升效率上具有一定优势。 表2 TDTS算法与传统分类算法准确率对比Tab.2 Accuracy comparison between TDTS and traditional classification algorithms 表3 FastShapelet算法在不同数据集下的分类准确率 %Tab.3 Classification accuracy of FastShapelet algorithm in different datasets % 表4 算法运行时间对比Tab. 4 Comparison of running time 本文提出了一种基于趋势特征的多样化top-kshapelet查询方法,解决了现存的shapelet分类算法不能很好地捕捉时间序列趋势信息的问题。通过将趋势特征符号化与FastShapelet进行结合,选出包含有趋势信息的shapelets,并利用多样化查询的方法对shapelet去除冗余,利用shapelets转换技术对时间序列进行分类。实验结果表明,算法能够有效地提高时间序列的分类效率,提高了算法的运行效率,缩短了算法的运行时间,并在趋势信息明显的数据上效果显著。但由于算法在进行shapelet发现的过程中着重保留了时间序列的趋势信息,应用在部分趋势信息较弱的时间序列时,分类效果会差于趋势特征明显的数据,因此在这方面还有待提高。 References) [1] YE L, KEOGH E. Time series shapelets: a new primitive for data mining [C]// KDD ’09: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2009: 947-956. [2] MUEEN A, KEOGH E, YOUNG N. Logical-shapelets: an expressive primitive for time series classification [C]// KDD’11: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2011: 1154-1162. [3] ZAKARIA J, MUEEN A, KEOGH E. Clustering time series using unsupervised-shapelets [C]// ICDM 2012: Proceedings of the IEEE 12th International Conference on Data Mining. Washington, DC: IEEE Computer Society, 2012: 785-794. [4] YE L, KEOGH E. Time series shapelets: a novel technique that allows accurate, interpretable and fast classification [J]. Data Mining and Knowledge Discovery, 2011, 22(1/2): 149-182. [5] LINES J, DAVIS L M, HILLS J, et al. A shapelet transform for time series classification [C]// KDD ’12: Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2012: 289-297. [6] 原继东,王志海,韩萌.基于Shapelet剪枝和覆盖的时间序列分类算法[J].软件学报,2015,26(9):2311-2325. (YUAN J D, WANG Z H, HAN M. Shapelet pruning and shapelet coverage for time series classification [J]. Journal of Software, 2015, 26(9):2311-2325.) [7] LIN J, KEOGH E, LONARDI S, et al. A symbolic representation of time series, with implications for streaming algorithms [C]// DMKD ’03: Proceedings of the 8th ACM SIDMOD Workshop on Research Issues in Data Mining and Knowledge Discovery. New York: ACM, 2003: 2-11. [8] LIN J, KEOGH E, WEI L, et al. Experiencing SAX: a novel symbolic representation of time series [J]. Data Mining and Knowledge Discovery, 2007, 15(2): 107-144. [9] RAKTHANMANON T, KEOGH E. Fast shapelets: a scalable algorithm for discovering time series shapelets [C]// SDM 2013: Proceedings of the thirteenth SIAM Conference on Data Mining. Philadelphia, PA: SIAM, 2013: 668-676. [10] BUHLER J, TOMPA M. Finding motifs using random projections [J]. Journal of Computation Biology, 2001, 9(2): 225-242. [11] QIN L, YU J X, CHANG L. Diversifying top-kresults [J]. Proceedings of the VLDB Endowment, 2012, 5(11): 1124-1135. [12] 孙其法,闫秋艳,闫欣鸣.基于多样化top-kshapelets转换的时间序列分类方法[J].计算机应用,2017,37(2):335-340. (SUN Q F, YAN Q Y, YAN X M. Diversified top-kshapelets transform for time series classcation [J]. Journal of Computer Applications, 2017, 37(2): 335-340.) [13] YIN H, YANG S-Q, ZHU X-Q, et al. Symbolic representation based on trend features for knowledge discovery in long time series [J]. Frontiers of Information Technology & Electronic Engineering, 2015, 16(9): 744-758. [14] YAN Q, SUN Q, YAN X. Adapting ELM to time series classification: a novel diversified top-kshapelets extraction method [C]// Proceedings of the 27th Australasian Database Conference on Databases Theory and Applications, LNCS 9877. Berlin: Springer-Verlag, 2016: 215-227. [15] CHEN Y, KEOGH E, HU B, et al. The UCR time series classification archive [DB/OL]. [2015- 07- 01]. http://www.cs.ucr.edu/~eamonn/time_series_data/. [16] CANDANEDO L M, FELDHEIM V. Accurate occupancy detection of an office room from light, temperature, humidity and CO2 measurements using statistical learning models [J]. Energy and Buildings, 2016, 112: 28-39. This work is partially supported by the National Key Research and Development Program (2016YFC060908), the National Natural Science Foundation of China (61402482, 61572505, 51674255), the Natural Science Foundation of Jiangsu Province (BK20140192). YANXinming, born in 1993, M. S. candidate. Her research interests include time series data mining. MENGFanrong, born in 1962, Ph. D., professor. Her research interests include database, data mining. YANQiuyan, born in 1978, Ph. D., associate professor. Her research interests include time series data mining, machine learning. Shapeletclassificationmethodbasedontrendfeaturerepresentation YAN Xinming*, MENG Fanrong, YAN Qiuyan (SchoolofComputerScienceandTechnology,ChinaUniversityofMiningandTechnology,XuzhouJiangsu221116,China) Shapelet is a kind of recognizable time series sub-sequence, by identifying the local characteristics to achieve the purpose of accurate classification of time series. The original shapelet discovery algorithm has low efficiency, and much work has focused on improving the efficiency of shapelet discovery. However, for the time series with trend change, the typical time series representation is used for shapelet discovery, which tends to cause the loss of trend information in the sequence. In order to solve this problem, a new trend-based diversified top-kshapelet classification method was proposed. Firstly, the method of trend feature symbolization was used to represent the trend information of time series. Then, the shapelet candidate set was obtained according to the trend signature of the sequence. Finally, the most representativekshapelets were selected from the candidate set by introducing the diversifying top-kquery algorithm. Experimental results of time series classification show that compared with the traditional classification algorithms, the accuracy of the proposed method was improved on 11 experimental data sets; compared with FastShapelet algorithm, the efficiency was improved, the running time of the proposed method was shortened, specially for the data with obvious trend information. The experimental results indicate that the proposed method can effectively improve the accuracy and the effciency of time series classification. shapelet; trend feature; symbolization; diversified top-kquery; time series classification TP311.13 A 2017- 02- 22; 2017- 05- 03。 国家重点研发计划项目(2016YFC060908);国家自然科学基金资助项目(61402482,61572505,52674255);江苏省自然科学基金资助项目(BK20140192)。 闫欣鸣(1993—),女,江苏徐州人,硕士研究生,主要研究方向:时间序列数据挖掘; 孟凡荣(1962—),女,辽宁沈阳人,教授,博士,主要研究方向:数据库、数据挖掘; 闫秋艳(1978—),女,江苏徐州人,副教授,博士,主要研究方向:时间序列数据挖掘、机器学习。 1001- 9081(2017)08- 2343- 06 10.11772/j.issn.1001- 9081.2017.08.2343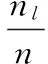


2 趋势特征表示的shapelet分类方法
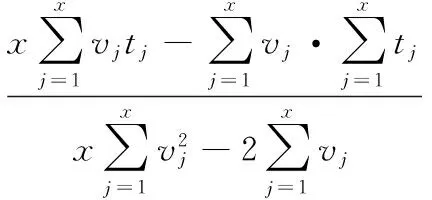


3 实验结果与分析





4 结语
