基于多尺度量子谐振子算法的相空间概率聚类算法
2017-10-21王梓懿安俊秀
王梓懿,安俊秀,王 鹏
(1.成都信息工程大学 并行计算实验室,成都 610225; 2.西南民族大学 计算机科学与技术学院,成都 610225)
(*通信作者电子邮箱86631589@qq.com)
基于多尺度量子谐振子算法的相空间概率聚类算法
王梓懿1,安俊秀1*,王 鹏2
(1.成都信息工程大学 并行计算实验室,成都 610225; 2.西南民族大学 计算机科学与技术学院,成都 610225)
(*通信作者电子邮箱86631589@qq.com)
针对大型集群难以进行任务调度和资源分配的问题,提出一种基于多尺度量子谐振子算法的相空间概率聚类算法(PSPCA-MQHOA)。首先,将集群工作状态投影到相空间中,把复杂的集群工作状态转化为相空间中的点集;进而,将相空间网格化,形成多尺度量子谐振子算法(MQHOA)以处理离散目标函数;最后,利用MQHOA优化过程中波函数变化的概率解释对集群节点进行概率聚类。PSPCA-MQHOA继承了MQHOA物理模型明确、搜索能力强、结果精确等优点,并且由于以相空间作为离散化的目标函数,迭代次数大大减少。实验结果表明PSPCA-MQHOA能适用于多种负载状态的集群。
概率聚类;量子谐振子;相空间;波函数;集群
0 引言
随着云计算技术的大面积普及与应用,集群的规模将越来越大[1];同时节点间频繁的迁移、备份、失效处理等高耦合性操作对集群的任务调度和资源分配造成了巨大的困难[2-4]。一种有效的处理方案是:把集群节点按照工作状态聚类,同一聚类中的节点具有相同的负载状态,如CPU占用率、内存占用率、I/O吞吐量、磁盘空间、网络通信状态等。文献[5]运用模糊聚类技术把计算机划分成若干个能力均衡的逻辑集群;文献[6]使用改进的C均值聚类算法计算出集群节点聚类中心和分类结果。但是目前所有聚类算法都不能保证完全准确地把每一个实例划分到合理的类,如果给出节点属于各个类的概率来形成概率聚类,将有助于消除传统聚类问题中硬性而快速的判断方案引发的脆弱性[7]。在聚类的实际应用中已经有学者使用了概率模型[8-10],然而使用概率模型对集群节点按工作状态聚类的应用尚未见诸文献。
对相空间理论的研究发现,传统相空间同样适用于云计算系统的分析。文献[11]首次提出云计算相空间的概念,为分析云计算集群提供了思路;文献[12]提出了多尺度量子谐振子算法(Multi-scale Quantum Harmonic Oscillator Algorithm, MQHOA),其在收敛过程中波函数的特征对集群概率聚类具有启发作用;文献[13]基于MQHOA的高斯采样提出了一种聚类中心选取算法,证明了MQHOA用于聚类的可行性,但该算法不适用于密度分布呈多峰特性的数据集。本文在相空间的基础上利用多尺度量子谐振子算法的搜索聚焦能力,根据其收敛过程中波函数变化的概率解释,提出了基于多尺度量子谐振子算法的相空间概率聚类算法(Phase Space Probabilistic Clustering Algorithm base on Multi-scale Quantum Harmonic Oscillator Algorithm, PSPCA-MQHOA),并通过三种模拟集群实验验证了PSPCA-MQHOA能适用于多种负载状态的集群。
1 相空间模型与多尺度量子谐振子算法
1.1 相空间投影与网格化
目前基于云计算相空间的研究已经有一定的成果[14-16]。文献[11]给出了云计算相空间的一般定义:在云计算系统中以服务器的n个工作状态参数为坐标轴所形成的n维空间称为云计算系统的相空间。
对于只考虑两个工作状态x和y的拥有p个节点的集群,可以由相空间中的点集C表示:C={(xi,yi):i≤p}。某集群节点的CPU占用率和内存占用率在相空间中的投影如图1所示,进一步将相空间划分为n×n的网格,根据每个网格在相空间中的位置附加坐标,投影到相空间的节点就必然落入某一个网格中。

图1 网格化相空间投影Fig. 1 Meshed phase space projection
将相空间如上述过程网格化后便可以运用MQHOA对节点进行聚类。如果把每一个网格当成一个点,落在网格中的节点数量当成函数值,整个相空间就可以抽象为一个离散的目标函数F(x,y),其定义域为:1≤x≤n2, 1≤y≤n2(x,y为整数)。此时网格取代连续目标函数中的点成为最小的计算单位,落入网格中的节点越多视为更优的采样位置,聚类的过程转化为优化问题,网格划分得越密计算的结果越精确。
1.2 多尺度量子谐振子算法在PSPCA-MQHOA中的应用
量子力学以其完备的理论成为现代物理学的基础支柱之一,在多种技术中得到了广泛的应用,其中量子谐振子的运动规律对优化问题有重要的启示。多尺度量子谐振子算法(MQHOA)就是一种模仿量子谐振子从高能态向基态收敛过程的函数优化算法,文献[17]详细介绍了其物理模型。MQHOA的波函数表示了目标函数在定义域上最优解出现位置的概率密度,由算法在函数优化的收敛过程中高斯函数的叠加形成。文献[12]给出了MQHOA在高维坐标分量xi的归一化波函数公式:

(1)
PSPCA-MQHOA的概率聚类过程就是寻找网格化相空间中局部包含节点最多的网格的过程,其波函数表示了网格化相空间中包含节点最多的网格出现位置的概率密度,以此波函数可以确定聚类个数,计算各网格中节点分属于各聚类的概率。PSPCA-MQHOA过程可以视为MQHOA对一个离散目标函数的多峰优化过程。
2 PSPCA-MQHOA
2.1 PSPCA-MQHOA原理分析

如图2为尺度收敛下采样网格的移动情况,图中网格中的数字表示被投影到该网格的节点数,被阴影覆盖的网格为当前采样网格,图2(a)~(d)分别为尺度在12.5、6.25、3.125、1.562 5下的采样网格位置,从中可以看出随着算法尺度的收敛,采样网格朝着局部节点数最多的网格聚拢。

图2 尺度收敛下采样网格的移动情况Fig. 2 Movement of sampling mesh under scale convergence
2.2 PSPCA-MQHOA基本流程
算法1 PSPCA-MQHOA。
输入 集群状态相空间,采样网格个数k,采样参数m,算法停止尺度σ,搜索尺度σs;
输出 集群节点概率聚类的结果。
步骤1 把集群状态相空间划分为n×n的网格,随机生成k个初始采样网格。

步骤3 若k个采样网格位置标准差变化量的最大值MAX(Δσk)满足MAX(Δσk)≥σs,则返回步骤2,否则进入步骤4。
步骤4 若σs≥σ,搜索尺度减半σs=σs/2,返回步骤2;否则算法结束,此时的波函数图像就表示集群的概率聚类。
PSPCA-MQHOA的迭代过程由嵌套的两种收敛组成:多尺度收敛和量子谐振子收敛。其中多尺度收敛的次数在网格划分完成后是固定不变的;对于量子谐振子收敛,后续的实验表明其次数在同一尺度下通常为1。
2.3 算法结果分析
PSPCA-MQHOA的输出结果为在停止尺度σ下的波函数,由于PSPCA-MQHOA的波函数表示了包含节点最多的网格出现位置的概率分布,所以波函数图像波峰的位置就是节点数最多的网格最有可能出现的位置,即聚类的中心,波峰的数量则是聚类的数量。类似于量子谐振子处于基态时波函数由多个高斯函数叠加形成,此时的波函数由多个高斯函数在聚类中心处叠加形成。将组成波函数的若干个高斯函数分离出来单独讨论可知,每一个高斯函数都是由数个采样网格在某处聚集形成,则此处必然是一个全局或局部节点数最密集的区域,自然地在这个区域就存在着一个聚类。若将每一个高斯函数代表一个聚类,那么高斯函数的函数值就是网格中节点属于其代表聚类的概率贡献,因此每一个网格中的节点都有属于各个聚类的概率贡献,将其归一化后就得出了节点属于各个聚类的概率。综上所述,对算法输出的波函数进行如下处理后形成了集群节点的概率聚类:
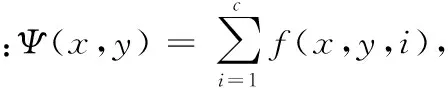
3 实验分析
本章在二维相空间下对PSPCA-MQHOA进行实验,对算法参数进行分析,以确定实验中使用的算法停止尺度σ、采样网格个数k和采样参数m的选取;然后对三种模拟集群的工作状态进行概率聚类实验,输出其波函数图像,并与传统聚类算法进行比较。
3.1 实验参数的分析
PSPCA-MQHOA的精确性与网格的划分有密切关系,网格划分得越密算法的结果越精确,然而计算开销越大。实际情况中需要根据集群中节点的数量动态调整网格划分的密度,因此不详细讨论网格的划分密度。为确定实验参数使用的测试数据为拥有四个聚类中心的二维数据集,其在相空间的投影如图3所示,并假设相空间划分为n×n个网格,参数k、m、σ将以n的倍数进行取值。
3.1.1 算法停止尺度σ的分析与选取
算法停止尺度σ的取值直接关系着波函数的形态,σ取值过大则算法过早停止,波函数在聚类位置叠加次数不足,如图4(a)所示为σ=n/2时波函数的俯视图;σ取值过小则算法收敛过度,波函数在聚类中心处过度叠加,如图4(b)所示为σ=n/30时波函数的正视图。实验的σ取值为n/2与n/30之间的一个合适的中间值σ=n/10,其波函数图像俯视图如图4(c)所示。

图3 四聚类中心测试数据集Fig. 3 Test data set with four clustering centers

图4 σ不同取值下的波函数图像Fig. 4 Wave function images with different values of σ
3.1.2 采样网格个数k、采样参数m的分析与选取
PSPCA-MQHOA参数k、m的选取会影响算法得到的聚类个数和聚类的位置。通过使用召回率(Recall)和精确率(Precision)来衡量k、m取值不同时算法测试结果的好坏。其中:召回率R侧重于考查算法的查全率,计算方式如式(2)所示;精确率P侧重于考查算法的查准率,计算方式如式(3)所示。
R=算法得出的与测试数据吻合的聚类数/测试数据的聚类数
(2)
P=算法得出的与测试数据吻合的聚类数/算法得出的所有聚类数
(3)
以相空间网格密度n的不同倍数对参数k、m进行取值,组成若干个不同的k、m参数组合,对测试数据进行聚类实验,记录10次实验的平均召回率和精确率,如表1所示。从表1可以看出,参数k、m共同影响算法的召回率和精确率。当k较小时,算法的召回率较低,这是因为采样网格数过少,无法全面覆盖所有局部节点最多的网格;当m较小时,算法的精准率较低,这是因为算法以高斯采样寻找更优网格的次数过少,采样网格没有完全聚集到局部节点最多的网格。随着参数k、m取值的增大,算法的召回率和精确率趋近于1。理论上参数k、m越大算法越稳定,计算开销也越大。同时考虑到算法的稳定性与效率,实验参数k、m的取值为:k=n×1.5,m=n×2.0。
3.2 概率聚类实验
实验使用的数据为三种不同负载状态下的模拟集群Cluster1、Cluster2、Cluster3。其中:Cluster1处于低负荷状态;Cluster2处于负载不均衡状态;Cluster3中有两组节点负荷相似。它们在网格化的相空间投影如图5所示。
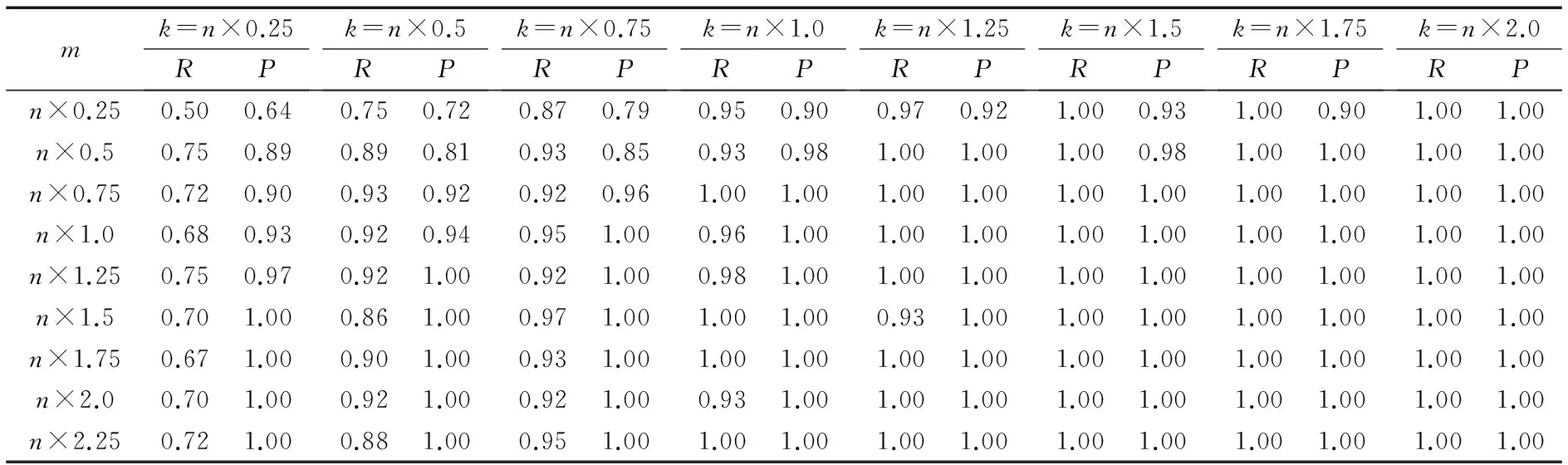
表1 不同k、m取值下平均召回率和精确率Tab. 1 Average recall rate and precision rate of different k, m values

图5 三种模拟集群相空间投影图Fig. 5 Phase space projection of three simulated clusters
下面使用PSPCA-MQHOA对上述三种集群按工作状态进行概率聚类,网格密度n为20,实验参数为σ=n/10,k=n×1.5,m=n×2.0。算法输出的波函数如图6所示。从图6可以看出,PSPCA-MQHOA的波函数图像正好对应了集群节点的聚类情况,算法不仅可以应用在节点数量少、负载状态单一的集群,对节点数量多、负载不均衡的集群也同样适用,同时能区分集群中负载状态十分相似的节点。
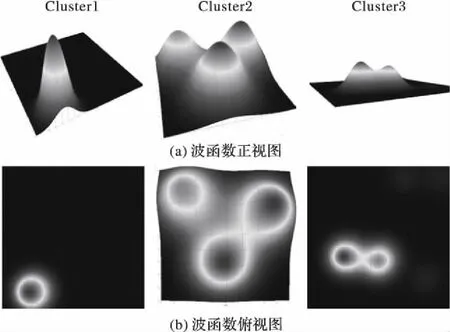
图6 三种集群数据的波函数图像Fig. 6 Wave function images of three clusters
在算法的两种收敛中,量子谐振子收敛的次数由采样网格移动情况与当前搜索尺度的关系决定,上述实验中这种关系如图7所示。从图7中可以看出,采样网格位置标准差变化量的最大值均小于当前搜索尺度,即每次量子谐振子收敛过程中,只需进行一次高斯采样便可生成满足条件的采样网格,当前尺度下量子谐振子收敛次数为1。这是由于网格化的相空间是一个定义域取值范围很小的离散目标函数,每次采样后网格位置的变化都非常小。因此,PSPCA-MQHOA的性能只与网格划分、集群工作状态数量和参数k、m有关,与相空间的投影情况(即集群负载情况)无关。
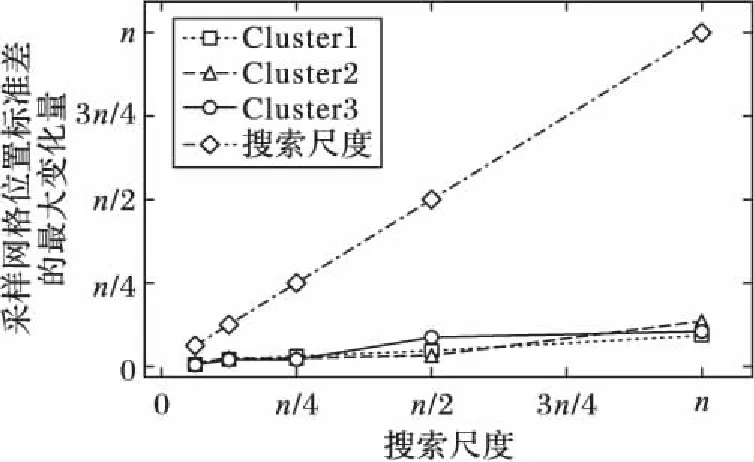
图7 采样网格标准差变化量与搜索尺度的关系Fig. 7 Relationship between variation of standard deviation of sampling grid and search scale
使用2.3节所述的方法将集群节点进行聚类,并将聚类结果与经典聚类算法K-means和DBSCAN(Density-Based Spatial Clustering of Applications with Noise)进行比较,如表2所示,其中K-means算法在数据集Cluster1、Cluster2、Cluster3中K取值分别为1、3、2。
从表2可以看出:对于Cluster1,由于聚类只有一个,各算法的效果相当;对于Cluster2和Cluster3,K-means算法的效果最好,但K-means算法比较依赖K的设定。在不需要提前设定聚类个数的算法中,PSPCA-MQHOA的效果略好于DBSCAN算法。

表2 不同聚类算法的正确率比较Tab. 2 Accuracy comparison of different clustering algorithms
4 结语
PSPCA-MQHOA将相空间离散化后作为MQHOA的目标函数,将普通的聚类问题转化为MQHOA的多峰优化问题,并用波函数表示集群的概率聚类。通过对三种模拟集群的聚类实验,验证了PSPCA-MQHOA能适用于多种负载状态的集群,并且算法具有迭代次数少、结果直观明确等优点。使用波函数对集群节点进行概率聚类也给云计算系统分析、云计算监控、负载均衡调度等工作提供了新思路。
References)
[1] 陈康,郑纬民.云计算:系统实例与研究现状[J]. 软件学报,2009,20(5):1337-1348. (CHEN K, ZHENG W M. Cloud computing:system instances and current research [J]. Journal of Software, 2009, 20(5): 1337-1348.)
[2] 李建锋,彭舰.云计算环境下基于改进遗传算法的任务调度算法[J]. 计算机应用,2011,31(1):184-186. (LI J F, PENG J. Task scheduling algorithm based on improved genetic algorithm in cloud computing environment [J]. Journal of Computer Applications, 2011, 31(1): 184-186.)
[3] 华夏渝,郑骏,胡文心.基于云计算环境的蚁群优化计算资源分配算法[J]. 华东师范大学学报(自然科学版),2010(1):127-134. (HUA X Y, ZHENG J, HU W X. Ant colony optimization algorithm for computing resource allocation based on cloud computing environment [J]. Journal of East China Normal University (Natural Science), 2010(1): 127-134.)
[4] ERGU D, KOU G, PENG Y, et al. The analytic hierarchy process: task scheduling and resource allocation in cloud computing environment [J]. The Journal of Supercomputing, 2013, 64(3): 835-848.
[5] 刘伯成,陈庆奎.云计算中的集群资源模糊聚类划分模型[J].计算机科学,2011,38(10A):157-160,168. (LIU B C, CHEN Q K. Fuzzy clustering partition model for computer cluster in cloud computing [J]. Computer Science, 2011, 38(10A): 157-160,168.)
[6] 姚婧,何聚厚.基于模糊聚类分析的云计算负载平衡策略[J].计算机应用,2012,32(1):213-217. (YAO J, HE J H. Load balance strategy of cloud computing based on fuzzy clustering analysis [J]. Journal of Computer Applications, 2012, 32(1):213-217.)
[7] WITTEN I H, FRANK E, HALL M A. Data Mining: Practical Machine Learning Tools and Techniques [M]. 3rd ed. San Francisco, CA: Morgan Kaufmann Publishers Inc., 2011: 285-287.
[8] MADDAH M, WELLS W M, Ⅲ, WARFIELD S K, et al. Probabilistic clustering and quantitative analysis of white matter fiber tracts [C]// IPMI 2007: Proceedings of the 20th International Conference on Information Processing in Medical Imaging, LNCS 4584. Berlin: Springer-Verlag, 2007: 372-383.
[9] VOGT J E, KLOFT M, STARK S, et al. Probabilistic clustering of time-evolving distance data [J]. Machine Learning, 2015, 100(2/3): 635-654.
[10] LU Z, LEEN T K. Penalized probabilistic clustering [J]. Neural Computation, 2007, 19(6): 1528-1567.
[11] 王鹏.云计算系统相空间广义热力学参数定义及分析[J].计算机应用,2012,32(8):2172-2175. (WANG P. Definitions and analysis of general thermodynamic parameters in cloud computing phase space [J]. Journal of Computer Applications, 2012, 32(8): 2172-2175.)
[12] 王鹏,黄焱,任超,等.多尺度量子谐振子高维函数全局优化算法[J].电子学报,2013,41(12):2468-2473. (WANG P, HUANG Y, REN C, et al. Multi-scale quantum harmonic oscillator for high-dimensional function global optimization algorithm [J]. Acta Electronica Sinica, 2013, 41(12): 2468-2473.)
[13] 燕京京,王鹏,范家兵,等.基于量子谐振子模型的聚类中心选取算法[J].电子学报,2016,44(2):405-412. (YAN J J, WANG P, FAN J B, et al. Clustering center selecting algorithm based on quantum harmonic oscillator model [J]. Acta Electronica Sinica, 2016, 44(2): 405-412.)
[14] 张磊,王鹏,黄焱,等.基于相空间的云计算仿真系统研究与设计[J].计算机科学,2013,40(2):84-86. (ZHANG L, WANG P, HUANG Y, et al. Research and design of cloud computing simulation system based on phase space [J]. Computer Science, 2013, 40(2): 84-86.)
[15] 郭又铭,王鹏,唐华,等.基于相空间的云计算专用监控系统[J].计算机工程,2013,39(7):40-44. (GUO Y M, WANG P, TANG H, et al. Specialized cloud computing monitoring system based on phase space [J]. Computer Engineering, 2013, 39(7): 40-44.)
[16] 王鹏,黄焱,李坤,等.云计算集群相空间负载均衡度优先调度算法研究[J].计算机研究与发展,2014,51(5):1095-1107. (WANG P, HUANG Y, LI K, et al. Load balancing degree first algorithm on phase space for cloud computing cluster [J]. Journal of Computer Research andt Development, 2014, 51(5): 1095-1107.)
[17] 王鹏,黄焱.多尺度量子谐振子优化算法物理模型[J].计算机科学与探索,2015,9(10):1271-1280. (WANG P, HUANG Y. Physical model of multi-scale quantum harmonic oscillator optimization algorithm [J]. Journal of Frontiers of Computer Science and Technology, 2015, 9(10): 1271-1280.)
This work is partially supported by the National Natural Science Foundation of China (71673032).
WANGZiyi, born in 1993, M. S. candidate. His research interests include distributed computing, intelligent algorithm.
ANJunxiu, born in 1970, M. S., professor. Her research interests include social computing, distributed computing.
WANGPeng, born in 1975, Ph. D., professor. His research interests include distributed computing, intelligent algorithm.
Phasespaceprobabilisticclusteringalgorithmbasedonmulti-scalequantumharmonicoscillatoralgorithm
WANG Ziyi1, AN Junxiu1*, WANG Peng2
(1.ParallelComputingLaboratory,ChengduUniversityofInformationTechnology,ChengduSichuan610225,China;2.SchoolofComputerScienceandTechnology,SouthwestMinzuUniversity,ChengduSichuan610225,China)
A Phase Space Probabilistic Clustering Algorithm based on Multi-scale Quantum Harmonic Oscillator Algorithm (PSPCA-MQHOA) was proposed to solve the task scheduling and resource allocation of large clusters. Firstly, the cluster operating status was projected into the phase space, and the complex working state was transformed into the point set in the phase space. Furthermore, the phase space was meshed to form the Multi-scale Quantum Harmonic Oscillator Algorithm (MQHOA) for discrete objective function. Finally, probabilistic clustering of cluster nodes was carried out by using the probability interpretation of wave function in the MQHOA process. PSPCA-MQHOA inherits the advantages of MQHOA, such as explicit physical model, strong search capabilities and accurate results, and it has few iterations due to the discretized phase space. Experimental results show that PSPCA-MQHOA can be applied to clusters in a variety of load conditions.
probabilistic clustering; quantum harmonic oscillator; phase space; wave function; cluster
TP393.027.2
A
2017- 02- 15;
2017- 03- 13。
国家自然科学基金资助项目(71673032)。
王梓懿(1993—),男,广西贺州人,硕士研究生,主要研究方向:分布式计算、智能算法; 安俊秀(1970—),女,山西临汾人,教授,硕士,CCF会员,主要研究方向:社会计算、分布式计算; 王鹏(1975—),男,四川乐山人,教授,博士,CCF会员,主要研究方向:分布式计算、智能算法。
1001- 9081(2017)08- 2218- 05
10.11772/j.issn.1001- 9081.2017.08.2218
