基于熵分析法和分析法的换热网络适应性比较

冯园丽，夏力，项曙光



冯园丽，夏力，项曙光

（青岛科技大学过程系统工程研究所，山东青岛 266042）

能源是国民经济发展和人们生活水平的重要物质基础，能源的合理开发和有效利用对社会的发展和进步产生很大的影响。国家“十三五”规划建议提出推进能源革命，加快能源技术创新，建设清洁低碳、安全高效的现代能源体系，提高非化石能源比重，推动煤炭等化石能源清洁高效利用[1]。调整能源结构、提高能源利用率、推广节能技术已经成为我国优化过程能量系统和发展过程工业的内在需求。

热量输运过程的研究是化工过程中能量系统的基础环节，该过程的优化能够减少能量消耗，是化工过程系统节能的有效措施。在传热过程优化的研究中，PRIGOGINE[2]基于变分法提出最小熵产原理，BEJAN[3]提出的熵产最小原则，即给定换热速率，温差最小，熵产最小，可用能损失最小。NEVERS和SEADER[4-5]基于熵平衡方程式，定义损失功和热力学效率，从而提出了熵分析法。熵分析法在许多领域都有广泛研究，比如热力学[6-7]、生物学[8-9]、物理[10-11]、医学[12]、工程技术[13-14]，甚至哲学[15]、历史[16-17]和经济[18-19]等。目前，在化工过程工业的节能方面，熵分析法较多地用于优化换热器参数，较少用于双流股换热网络[20]，没有用于多流股换热网络中，且熵分析法存在一定的局限性：BEJAN[21]对换热器优化设计时，发现有效度随着熵产数增大而增大的“熵产悖论”现象；BERTOLA等[22]证明熵产最小原理优化导热和流体流动时，不适用于静止状态和傅里叶定律；ZHANG等[23]研究换热器的传热效果时，发现存在临界热平衡误差，使得出现无效负熵产的现象。

1 换热网络中的熵分析法和分析法

1.1 换热网络中的熵分析法

换热网络中的熵分析法是基于热力学第二定律，目的是研究在环境温度0下热物流对冷物流做的最大理想功。通过计算冷、热物流各自的熵变、焓变、理想功或根据冷、热物流的总熵变计算损失功，进一步求解热力学第二定律效率来作为评价换热网络能量回收效果的依据，有助于指导制定相应的节能措施。

假设换热网络中有h个热物流（包括热公用工程）和c个冷物流（包括冷公用工程），在换热过程中流体不存在相变，没有热量损失和轴功，流体的流动方式是逆流或并流，则从起始温度为in到终点温度为out的熵变为式(1)、式(2)[31]。

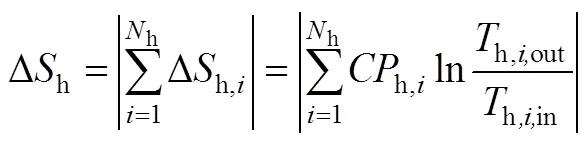
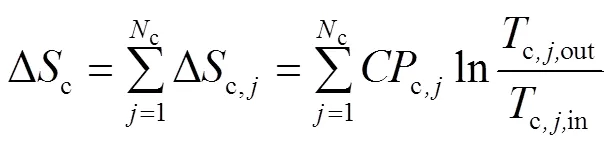
式中，为热容流率，即=质量流率×定压比热容c。

物流所做的理想功为式(3)、式(4)。

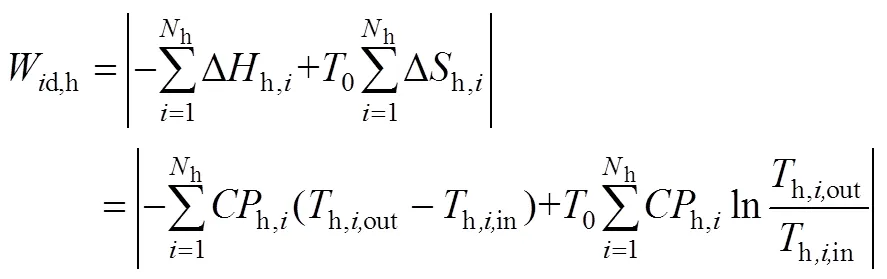
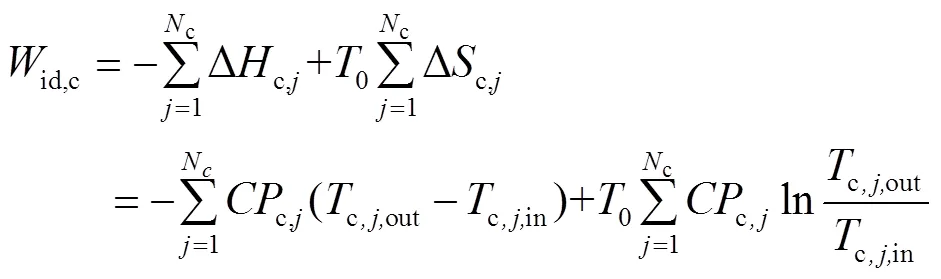
式中，Δ为焓变；0为环境温度。

换热网络的热力学第二定律效率为式(5)。

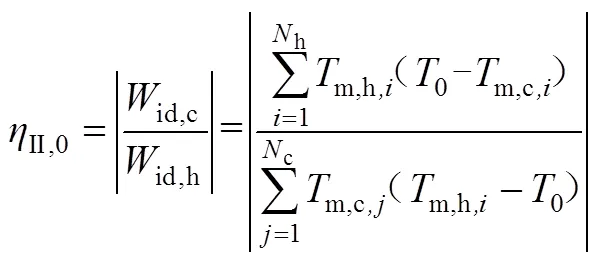
式中，m,h,i、m,c,j为股热物流和股冷物流的对数平均温度。

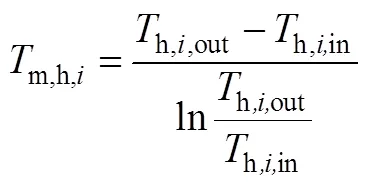
传热温差越大表明在换热网络中热物流的热量并不能较好地被冷物流利用，则损失功越大，热力学第二定律效率越低。通常Δmin=15~25K[32-33]，因此选择不同的传热温差，重复上述步骤，由式(5)分别得到热力学第二定律效率Ⅱ,1、Ⅱ,2…，通过比较来评价换热网络中的热量利用情况，确定最大热回收网络。

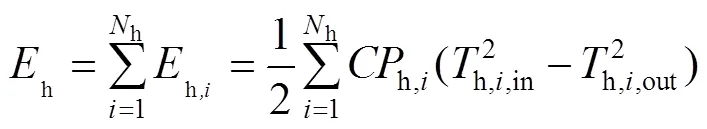
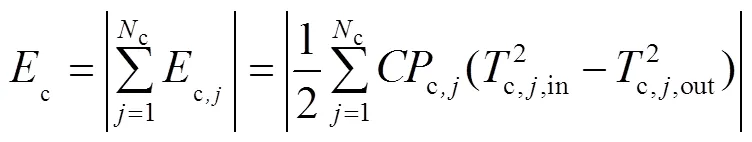
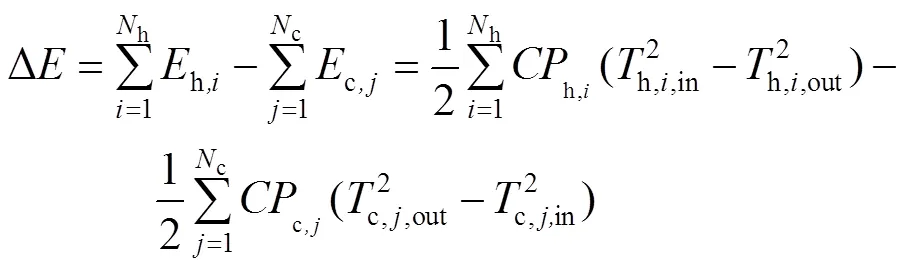
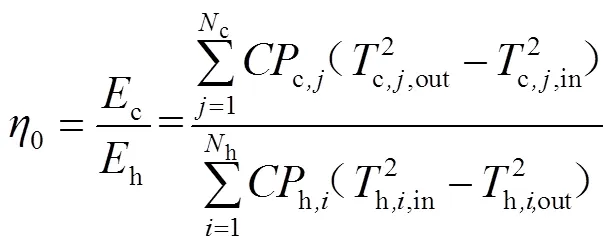
由式(1)、式(2)计算该过程的熵变，见式(10)。

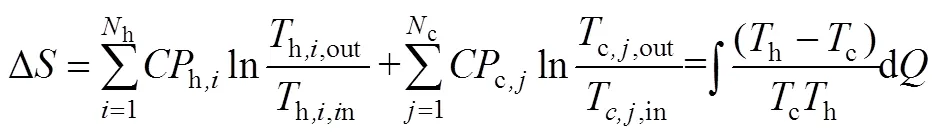
根据式(5)，可计算热力学第二定律效率为 式(13)。

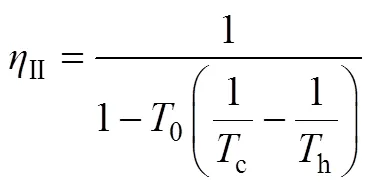
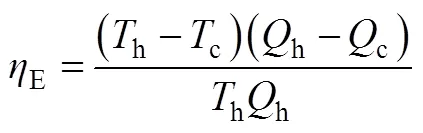
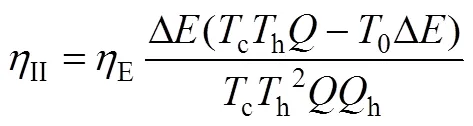
2 SSOT装置换热网络中两种分析方法的比较

SSOT装置是指重质油采用一次通过、加氢裂化尾油部分循环或全循环的方式操作进行加氢脱硫、脱氮等反应，是现代炼化企业二次加工、重质油轻质化的重要手段。案例中SSOT装置以减压瓦斯油为原料，经过预热与氢气混合后被加热到一定温度进入反应器进行加氢脱硫、脱氮、裂解及烯烃和芳烃饱和等反应，反应产物经冷高分、冷低分，冷高分顶循环气脱硫后返回到反应部分循环使用，冷低分酸性气输送到其余脱硫单元，冷低分来的生成油脱除H2S后，进入分馏塔将转化产品与转化产品分离，得到转化产品石脑油、航煤、柴油和作为乙烯生产原料的尾油。该装置的换热网络包括11股热物流和9股冷物流，提取物流数据见表1，冷、热公用工程数据见表2和 表3[38-39]。

2.1 现行换热网络分析

根据表1的数据，选取环境温度为0=298.15K，压力=0.1013MPa，在-图中绘制出冷、热组合曲线，见图1。

表1 工艺物流数据

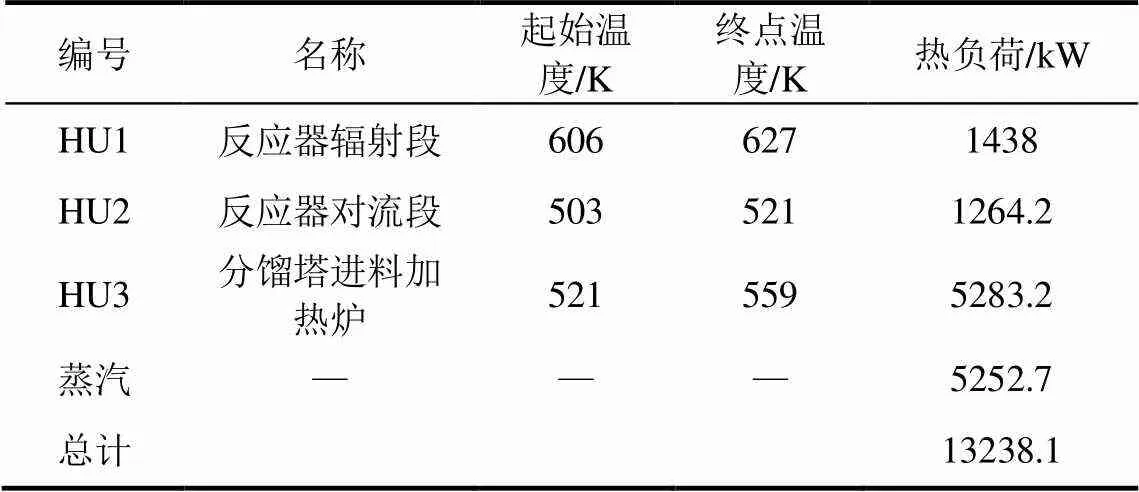
表2 热公用工程数据

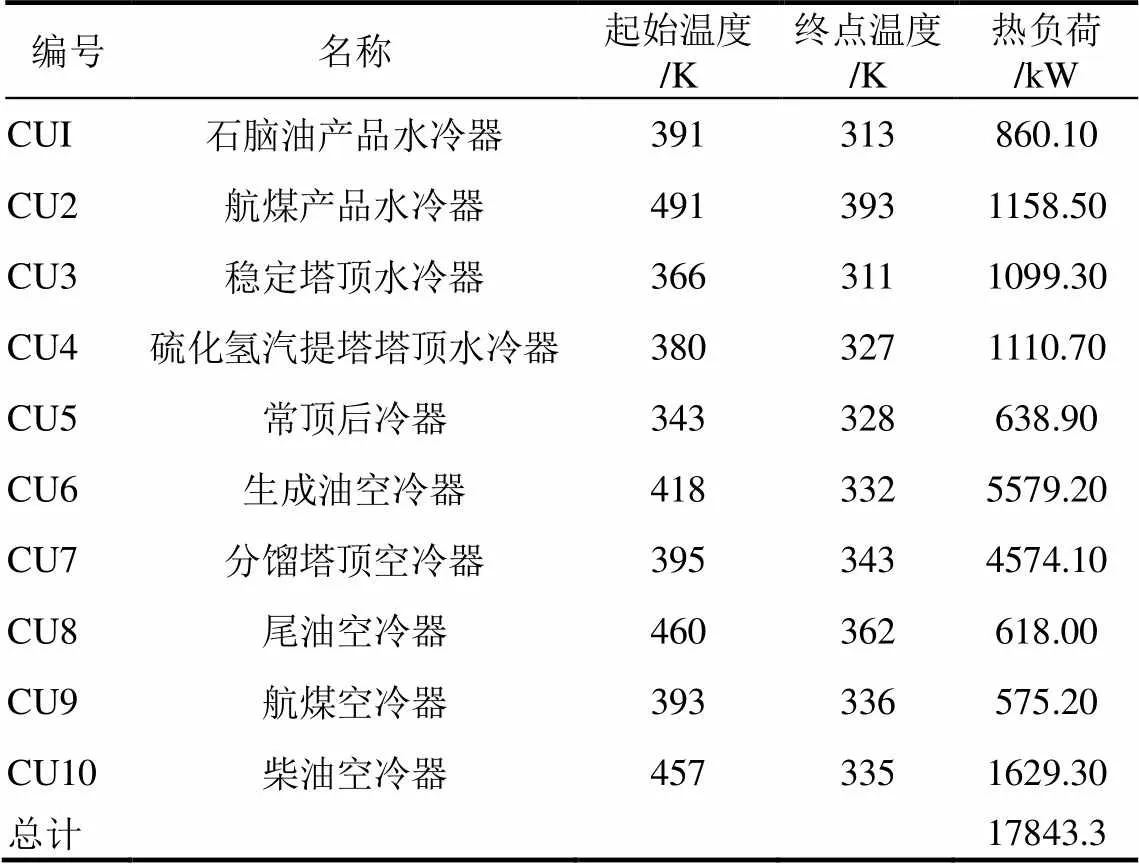
表3 冷公用工程数据

（1）熵分析法 热物流的熵变为97.861kW/K，热物流的理想功为1.547×104kW，冷物流的熵变为72.445kW/K，冷物流的理想功为1.264×104kW，外加热公用工程的熵变为14.073kW/K，理想功为3.670×103kW，冷公用工程的熵变为48.003kW/K，理想功为3.531×103kW，则热力学第二定律效率为81.70%。

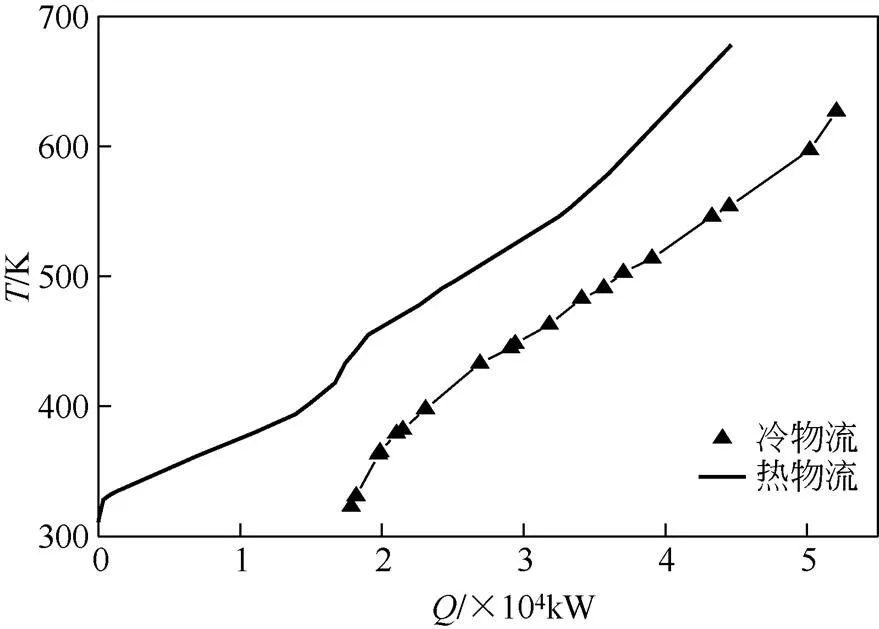
图1 SSOT装置现有换热网络的冷、热组合曲线图

2.2 最大能量回收下的换热网络分析

假设取Δmin=20K时，夹点温度为408K（位移温度），即对于热物流为418K，对于冷物流为398K，在-图中绘制最大热回收换热网络的冷、热组合曲线图见图2。

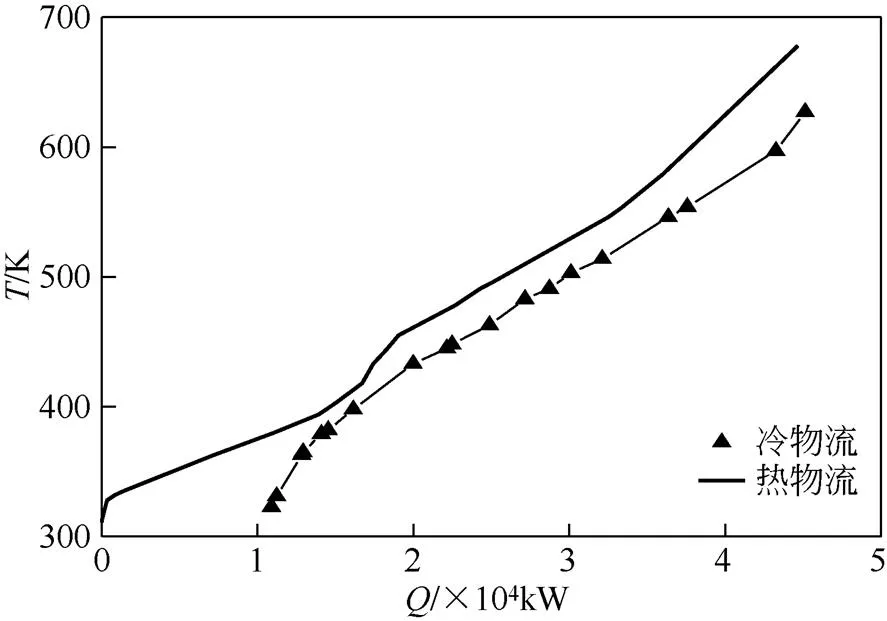
图2 SSOT装置最大热回收换热网络组合曲线图[38-39]

（1）熵分析法 热物流的熵变为1.002×102kW/K，热物流的理想功为1.479×104kW，冷物流的熵变为70.905kW/K，冷物流的理想功为1.310×104kW，外加热公用工程熵变为1.669kW/K，理想功为5.352×102kW，冷公用工程熵变为32.283kW/K，理想功为1.817×103kW，则热力学第二定律效率为88.59%，节能67.34%。

按照上述方法，分别再取Δmin=15K、25K，计算结果见表4、表5。

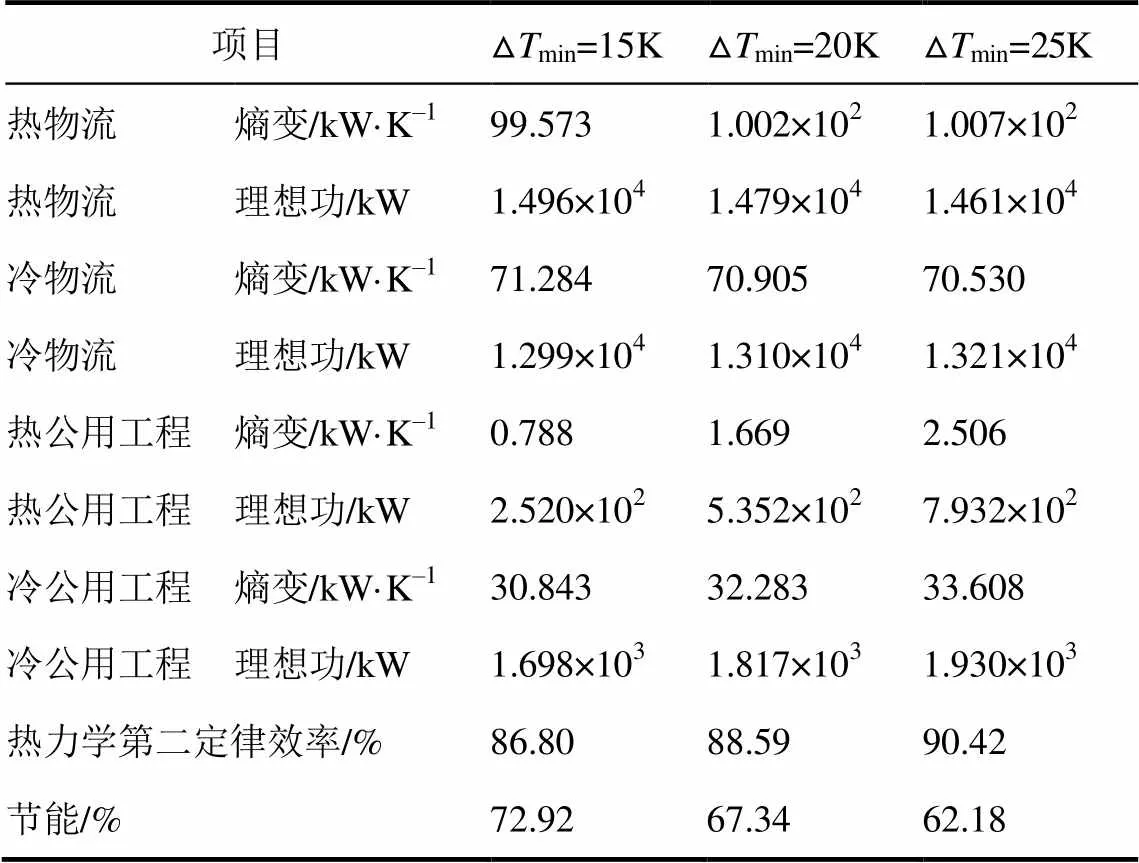
表4 熵分析法结果

表5 分析法结果

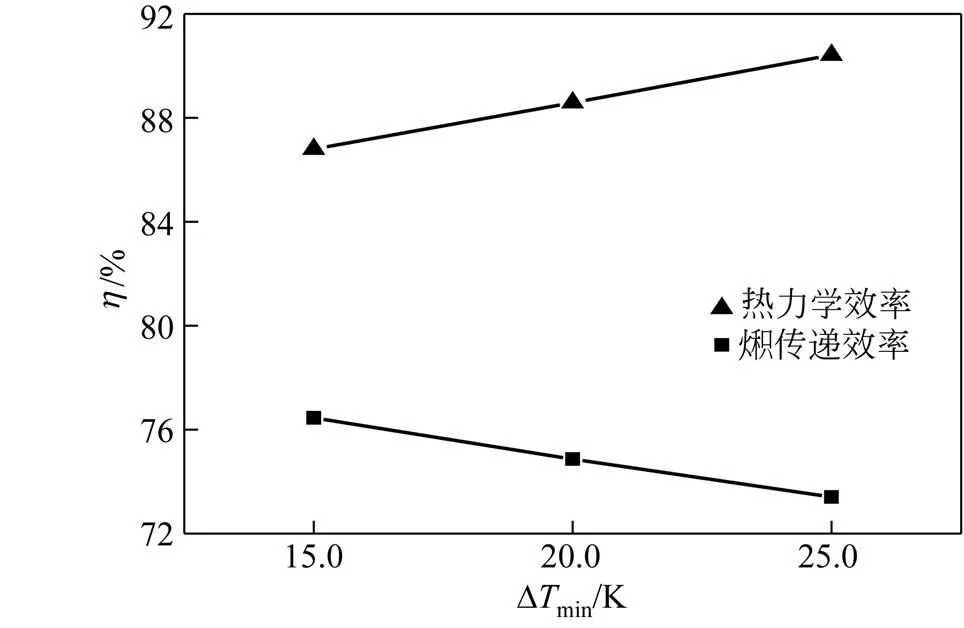
图3 热力学效率和传递效率随ΑΒΓΔTmin的变化

由图3和表4、表5可以看出，对于熵分析法，随着Δmin=15K、20K和25K变化时，热物流的熵变越来越大，所做的理想功越来越小；冷物流的熵变越来越小，所做的理想功越来越大，而热力学第二定律效率却越来越大，分别为86.80%、88.59%和90.42%。由式(1)知熵与热量和温度有关，当热量一定时，冷、热流体温差越小，总熵变越小，做功能力越强，根据BEJAN提出的熵产最小原则，熵变越小表明损失功越小。而案例中冷热流体的传热温差越大，反而总熵变越大，损失功越小，热力学效率越大，节能效果越差，出现违背熵产最小原则的现象。因此，熵分析法并不适用于描述换热网络的节能效果。

3 结论

符号说明

CP——热容流率，kW/K cv——定容比热容，kJ/(kg·K) cp——定压比热容，kJ/(kg·K) E——，kW·K ΔE——耗散，kW·K H——焓变，kW m ——质量流率，kg/s P——压力，MPa Q——热容量，J S——熵变，kW/K T——温度，K ΔTmin——最小传热温差，K W——功，kW ηII——热力学第二定律效率，% ηE——传递效率，% 下角标 c——冷物流 h——热物流 i, j——物流的组分数 m——对数平均 in——起始 out——终点 id——理想状态

[1] 国务院. 中华人民共和国国民经济和社会发展第十三个五年规划纲要[EB/OL]. 新华社，2016[2016-03-17]. http://www.china. com.cn/ lianghui/news/2016-03/17/content_38053101.htm

The State Council．The 13th Five-Year Plan for Economic and Social Development of the People’s Republic of China[EB/OL]. [2016-03- 17]. http://www.china.com.cn/lianghui/news/2016-03/17/content_ 38053101. htm

[2] PRIGOGINE I．Problèmes d'Évolution dans la Thermodynamique des Phénomènes Irréversibles[M]．The Origin of Life on the Earth (English-French-German Edition)．New York：Academic Press，1959：418-427．

[3] BEJAN A．Entropy generation minimization：the new thermodynamics of finite-size devices and finite-time processes[J]. Journal of Applied Physics，1996，79（3）：1191-1218．

[4] NEVERS N D，SEADER J D．Lost work：a measure of thermodynamic efficiency[J]．Energy，1980，5（8/9）：757-769．

[5] NEVERS N D，SEADER J D．Mechanical lost work，thermodynamic lost work，and thermodynamic efficiencies of processes[J]．Revista Latinoamericana De Transferencia De Calor Y Materia，1984，8（1/2）：77-105．

[6] BUTT A S，ALI A．Entropy analysis of magnetohydrodynamic flow and heat transfer over a convectively heated radially stretching surface[J]．Journal of the Taiwan Institute of Chemical Engineers，2014，45（4）：1197-1203．

[7] NATERER G．Transition criteria for entropy reduction of convective heat transfer from micropatterned surfaces[J]．Physical Review A，2015，87（4）：2940-2949．

[8] SHAW C A，SENEFF S，KETTE S D，et al．Aluminum-induced entropy in biological systems：implications for neurological disease[J]．Journal of Toxicology，2014（10）：1-27．

[9] BAEZ J C，POLLARD B S．Relative entropy in biological systems[J]．Entropy，2015，18（2）：1-22．

[10] GIFFIN A，CAFARO C，ALI S A．Application of the maximum relative entropy method to the physics of ferromagnetic materials[J]．Physica A：Statistical Mechanics and its Applications，2016，455（8）：11-26．

[11] DUBROCA B，BRULL S，MALLET J．General moment system for plasma physics based on minimum entropy principle[J]．Kinetic & Related Models，2015，8（3）：533-558．

[12] CRANE P W，ZHOU Y，SUN Y，et al．Entropy：a conceptual approach to measuring situation-level workload within emergency care and its relationship to emergency department crowding[J]．Journal of Emergency Medicine，2014，46（4）：551- 559．

[13] THARAYIL T，ASIRVATHAM L G，DAU M J，et al．Entropy generation analysis of a miniature loop heat pipe with grapheme-water nanofluid: Thermodynamics model and experimental study[J]．International Journal of Heat and Mass Transfer，2017，106（3）：407-421．

[14] MUNITZ A，MESHI L，KAUFMAN M J．Heat treatments' effects on the microstructure and mechanical properties of an equiatomic Al-Cr-Fe-Mn-Ni high entropy alloy[J]．Materials Science and Engineering：A，2017，689（3）：384-394．

[15] REUTLINGER A．Can Interventionists be Neo-Russellians? Interventionism，the open systems argument, and the arrow of entropy[J]．International Studies in the Philosophy of Science，2013，27（3）：273-293．

[16] DAVIES T，FRY H，WILSON A，et al．Application of an entropy maximizing and dynamics model for understanding settlement structure：the khabur triangle in the middle bronze and iron ages[J]．Journal of Archaeological Science，2014，43（2）：141-154．

[17] BUSTINCE H，BARRENECHEA E，PAGOLA M，et al．A historical account of types of fuzzy sets and their relationships[J]．IEEE Transactions on Fuzzy Systems，2016，24（1）：179-194．

[18] ARGENTIERO A，BOVI M，CERQUETI R．Bayesian estimation and entropy for economic dynamic stochastic models：an exploration of overconsumption[J]．Chaos Solitons & Fractals，2016，88：143-157．

[19] GO D S，LOFGREN H，RAMOS F M，et al．Estimating parameters and structural change in CGE models using a Bayesian cross-entropy estimation approach[J]．Economic Modelling，2016，52（18）：790-811．

[20] CHENG X T，LIANG X G．Computation of effectiveness of two-stream heat exchanger networks based on concepts of entropy generation, entransy dissipation and entransy-dissipation-based thermal resistance[J]．Energy Conversion and Management，2012，58：163-170．

[21] BEJAN A．Second-law analysis in heat transfer and thermal design[J]．Advances in Heat Transfer，1982，15：1-58．

[22] BERTOLA V，CAFARO E．A critical analysis of the minimum entropy production theorem and its application to heat and fluid flow[J]．International Journal of Heat and Mass Transfer，2008, 51（7-8）：1907-1912．

[23] ZHANG Z，ZHANG Y，ZHOU W，et al．Critical heat balance error for heat exchanger experiment based on entropy generation method[J]．Applied Thermal Engineering，2016，94（2）：644-649．

GUO Z Y，LIANG X G，ZHU H Y．Entransy—A physical quantity describing heat transfer ability[J]．Progress in Natural Science，2006，16（10）：1288–1296．

[25] 陈群，许云超，过增元. 传热学中的状态图及其应用[J].科学通报，2012，57（28）：2771-2777.

CHEN Q，XU Y C，GUO Z Y．The property diagram in heat transfer and its applications[J]．Chinese Science Bulletin，2012，57（28）：2771-2777．

[26] WU J，GUO Z Y．Application of entransy analysis in self-heat recuperation technology[J]．Industrial & Engineering Chemistry Research，2013，53（3）：1274-1285．

WANG Y F，CHEN Q．An entransy dissipation resistance-based method for optimization of heat exchanger networks[J]．Journal of Chemical Industry and Engineering（China），2015，66（s1）：272-276．

[28] XU Y C，CHEN Q，GUO Z Y．Optimization of heat exchanger networks based on lagrange multiplier method with the entransy balance equation as constraint[J]．International Journal of Heat and Mass Transfer，2016，95：109-115．

[29] 柳雄斌，过增元．换热器性能分析新方法[J]．物理学报，2009，58（7）：4766-4771.

LIU X B，GUO Z Y．A new method for performance analysis of heat exchangers[J]．Acta Physica Sinica，2009，58（7）：4766-4771．

[30] XU Y C，CHEN Q，GUO Z Y．Entransy dissipation-based constraint for optimization of heat exchanger networks in thermal systems[J]．Energy，2015，86（4）：696-708．

[31] 施云海．化工热力学[M]. 2版. 上海：华东理工大学出版社，2013：192-193.

SHI Y H．Chemical engineering thermodynamics[M]．2nd. Shanghai：East China University of Science and Technology Press，2013：192-193．

[32] 华贲，仵浩，刘二恒. 基于㶲经济评价的换热器最优传热温差[J]．化工进展，2009，28（7）：1142-1146．

HUA B，WU H，LIU E．Exergy-economics based method about optimal temperature difference in heat-exchanger[J].Chemical Industry and Engineering Progress，2009，28（7）：1142-1146．

[33] 肯普. 能量的有效利用-夹点分析与过程集成[M]. 项曙光，贾小平，夏力译. 北京：化学工业出版社，2010：69-70.

KEMP I C. Pinch analysis and process integration[M]. XIANG S G，JIA X P，XIA L. translation. Beijing：Chemical Industry Press，2010：69-70.

CHENG X G．Entransy and its applications in heat transfer optimization[D]．Beijing：Tsinghua University，2004．

[35] 施林德尔．换热器设计手册第三卷换热器的热设计与流动设计[M]. 北京：机械工业出版社，1988：1-2.

SCHLUNDER E U．Thermal and flow design of heat exchangers of the heat exchanger design handbook[M]．Beijing：China Machine Press，1988：1-2．

[36] VDI-Gesellschaft．VDI heat atlas[M]．Berlin：Springer，2010．

[37] 柳雄斌，孟继安，过增元．换热器参数优化中的熵产极值和火积耗散极值[J]. 科学通报，2008，53（24）：3026-3029．

LIU X B，MENG J A，GUO Z Y．Minimum entropy generation and minimum entransy dissipation in parameter optimization of heat exchanger[J]．Chinese Science Bulletin，2008，53（24）：3026-3029．

[38] 王凌燕，夏力，高凯，等．SSOT装置换热网络节能研究[J]．化工进展，2011，30（s1）：689-693．

WANG L Y，XIA L，GAO K，et al．Energy saving research on SSOT heat exchanger network[J]．Chemical Industry and Engineering Progress， 2011，30（s1）：689-693．

[39] 王凌燕．SSOT装置的模拟与节能研究[D]．青岛：青岛科技大学，2012．

WANG L Y．Studies on simulation and energy saving of SSOT device[D]．Qingdao：Qingdao University of Science and Technology， 2012．

Comparative study on heat exchanger network adaptability based on entropy analysis and entransy analysis

FENG Yuanli，XIA Li，XIANG Shuguang

（Institute of Process System Engineering，Qingdao University of Science and Technology，Qingdao 266042，Shandong，China）

Entropy and entransy are the measure of irreversibility of heat transfer process，which can be used to evaluate the utilization of energy in the heat exchanger networks（HENs）. In view of the irreversibility of HENs，firstly，the mathematical models of HENs energy efficiency were established based on entropy analysis method and entransy analysis method. Then, taking the maximum energy recovery as the goal，the HEN analysis of the single-stage once through hydrocracker （SSOT） unit was carried out. The applicability of the two methods was compared，and it was proved that the entropy analysis method is suitable for the analysis of complex HENs. The results showed that the minimum temperature differencesminwere selected 15K，20K，25K respectively，and the heat transfer efficiency calculated by the two methods were different. The efficiency of the second law of thermodynamics calculated by entropy analysis method increased 86.80%，88.59% and 90.42%，respectively，which was inconsistent with the principle of minimum entropy production. The entransy transfer efficiency decreased 76.45%，74.86%，73.41%，respectively. The results of entropy analysis method were consistent with the greater the temperature differences，the lower the heat transfer ability. Thus，the entransy analysis method is more suitable for the analysis of energy utilization efficiency of HENs than that of entropy analysis method. At the same time，this method is helpful to evaluate the energy saving potential of heat transfer network.

heat transfer；entropy；entransy；optimization；heat exchanger networks

TQ021.8

A

1000-6613（2017）10-3657-08

10.16085/j.issn.1000-6613.2017-0355

2017-03-07；

2017-06-05。

国家自然科学基金项目（21406124）。

冯园丽（1992—），女，硕士研究生。

项曙光，教授，博士生导师，研究方向为化工过程系统工程。E-mail：xsg@qust.edu.cn。