经验模式分解与代价敏感支持向量机在癫痫脑电信号分类中的应用*

李冬梅，张洋，杨日东，陈子怡，田翔华，董楠，尔西丁·买买提，周毅,△

(1. 新疆医科大学，新疆 乌鲁木齐 830011；2.新疆医科大学第一附属医院神经内科，新疆 乌鲁木齐 830011；3.中山大学中山医学院生物医学工程系，广东 广州 510080；4.中山大学附属第一医院神经内科，广东 广州 510080)

1 引 言

癫痫是一种常见的慢性脑部神经疾病，其发作来源于大脑神经元异常放电，引起中枢神经系统功能短暂性失常，表现为意识、感觉等多方面功能障碍，具有不确定性、发作性，严重影响患者的日常生活和工作。脑电图(electroencephalogram，EEG)的发展，对临床试验探测大脑皮层的脑活动和相关疾病提供了一种无创和低成本的有效技术[1]。脑电图表示的是通过脑电电极所记录到的各种脑电活动的总和[2]，癫痫患者的脑活动通常包括发作间期和发作期(在一些病例中存在癫痫发作的前期和后期)。从一种状态向另一种状态演变时，脑电信号会发生变化，大脑系统与此对应的各种动力学特征向量也随之产生变化[3]。脑电信号具有非平稳性和非线性特征，因此,对于脑电信号分析往往以传统的时域、频域或者时频结合的方法为主[4-7]，通过计算各种非线性的特征值来区分脑电信号[8]。大多数的数据预处理方法均是用小波变换对信号进行分解，而分层数、基函数的选择对结果有很大影响，不具备对信号自适应的分解能力[9-10]。

对癫痫脑电信号进行自动检测与识别的分类方法越来越多，主要有支持向量机(SVM)、决策树(DT)、随机森林(RandomForest)、模糊分类(FM)等。我们采用了代价敏感支持向量机(cost-sensitive support vector machine,CSVM)这一方法，其不仅具备了支持向量机(support vector machine，SVM)的特征，并且能够考虑到样本的不同误分类代价，实现代价敏感挖掘。本研究中，首先采用EMD算法将癫痫脑电数据进行分解，选取主要IMF分量，计算样本熵；使用核函数为RBF(rial basis function，RBF)的代价敏感支持向量机进行分类，先选取一例患者的脑电信号作为训练数据对分类器进行训练，然后选取不同的病例脑电信号作为测试数据进行分类，并使用K-CV(k-fold cross validation，K-CV)算法进行参数寻优，最后依据临床医师诊断得出分类结果。用这种测试方法不仅可以进一步提高分类的准确率，并且能对分类器的泛化能力和学习能力进行更准确的描述，对于临床上研究癫痫实时信号检测与识别更具有实际意义。

2 数据处理及特征提取

2.1 经验模式分解算法

EMD(empirical mode decomposition，EMD)是一种自适应信号时频分析方法，在处理脑电信号这一类非平稳非线性随机信号上具有明显的优势[11]。它可将信号分解成一系列的准单分量信号，即本征模函数(intrinsic mode function，IMF)。每一阶IMF包含了原始信号的不同频率信息，分析这些IMF即可获得信号的局部信息特征。

经验模式分解是由Huang等人提出的一种新的自适应信号时频处理方法，其本质是通过信号的时间尺度获得本征波动模式。EMD有三大假设[12-13]：(1)信号至少有一个极大值点和一个极小值点；(2)特征时间尺度由极值点的时间推移定义；(3)如果整个信号只包含曲折点而不包含极值点，可以先微分一次或者多次找到极值点，然后将所得到的分量进行积分得到最后结果。这样任何一个复杂信号都可以被分解成有限个具有物理意义的固有模态函数(IMF)，其中任何一个IMF满足以下两个约束条件：

(1)数据段内，极值点和零点数目要想等或者最多相差1；

(2)任何一点处，分别由局部极大值点和局部极小值点确定的包络线的均值为0。

EMD的具体步骤是：

(1)求出信号C(t)所有的极值点，并分别用一条光滑的曲线连接，使得两条曲线间包括所有的信号。上下包络线emax(t)和emin(t)的均值记作m1(t)，求出：

C(t)-m(t)=h1(t)

(1)

若h1(t)是一个固有模态分量，那么h1(t)就是C(t)的第一个分量。

(2)用h1(t)替代C(t)，重复之前的步骤，直到h1k(t)为一个IMF，记C1(t)=h1k(t)，并将C1(t)从信号C(t)中分离出来，得到：C(t)-c1(t)=r1(t)，并令C(t)=r1(t)；

(3)重复上述步骤，直到rN(t)或c1(t)满足预设条件，C(t)的分解结束。

一般来说，EMD分解出来IMF的前几个分量集中了原始信号中的主要信息。将EMD分解应用到脑电分析中，可为研究人员提供有价值的信息，避免了人为因素的干扰，更有利于提高脑电信号的分类准确率。

2.2 样本熵

EEG信号是一种非线性时间序列。常见的非线性动力学参数有关联维数、Lyapunov指数、近似熵、样本熵等，其中样本熵(sample entropy，SampleEn)是由Richman和Moornan提出的一种新的时间序列复杂性测度方法。可用于测量两个新信息发生的条件率。样本熵是一种与近似熵类似，但精度更好，可降低近似熵的误差。其具体算法如下：

设原始数据为x(1)，x(2)，…，x(N)，共N点。

(1)按序号连续顺序组成一组m维矢量：

X(i)=[x(i)，x(i+1)，…，x(i+m-1)]，i=1～N-m+1

(2)

(3)

(4)

(5)

(6)理论上此序列的样本熵为：

(6)

当N为有限值时上式表示为：

SampEn(m，r，N)=-ln[Bm+1(r)/Bm(r)]

(7)

SampEn的值显然与m，r的取值有关。不同的嵌入维数m和相似容限r对应的样本熵也不同。在一般情况下m=1或2,r=0.1SD～0.25SD(SD为标准差)计算得到的样本熵具有较为合理的统计特性，故本文所有样本熵的计算均取m=2，r=0.25SD。

大脑在癫痫发作时，神经元同步放电，各种脑功能都受到不同程度的抑制，因此与正常脑电活动相比，复杂度会有所降低。癫痫患者从发作间期到发作期，样本熵会有不同程度的下降，发作期结束后样本熵又会逐渐升高。

2.3 代价敏感支持向量机(CSVM)

传统分类算法通常假定每个样本的误分类具有同样的代价且每类样本数大致相等。但是现实的数据挖掘中这种假设是不成立的，因此取得的结果也不理想。考虑到不同样本的误分类具有不同的代价，提出代价敏感支持向量机(CSVM)的方法，对样本的错分采用不同的惩罚参数重新构造分类器，使其具有代价敏感的特性。

假设正常脑电为正类，癫痫脑电为负类。本研究对于正负类的训练错误引入不同的惩罚参数C+和C_对支持向量机进行训练，具体算法如下：

在训练集中T={(x1，y1)}，…，(xl，yl)}∈(X×Y)lxi为输入出样本，yi为输出样本，其中，xi∈X=Rn，yi∈Y={-1,1}，i=1，…，l。

选取径向基核函数(gaussian radial basis function,RBF)，其形式为：

K(xi，xj)=exp(-‖xi-xj‖2/σ2)

(8)

选取惩罚参数，构造并求解最优问题：

subject toyi((ω·xi)+b)≥1-ξi，ξi≥0，i=1，…，l

(9)

根据Lagrange函数，得到对偶问题：

0≤αi≤C+，i=1，2，…，l：yi=+1

0≤αi≤C-，i=1，2，…，l：yi=-1

(10)

(11)

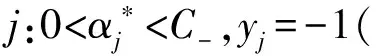
f(x)=sgn((ω*·x)+b*)

(12)

3 实验结果与分析

3.1 临床数据采集

实验数据来自于新疆医科大学第一附属医院神经科脑电图室，采样频率均为200 Hz。采用新疆医科大学第一附属医院神经科脑电图室某六位颞叶癫痫患者的数据，对六例患者的脑电数据描述如下：一例16岁颞叶患者(1号)的脑电数据诊断为发作间期118段与发作期118段，每段1500点数据；一例22岁颞叶患者(2号)的脑电数据发作间期至发作期330 s，共110段数据，每段1 500点数据、代表时间3 s，其中临床诊断在150～230 s为发作期，患者表现为左侧上肢抽搐；一例46岁颞叶患者(3号)的脑电数据发作间期至发作期160 s，共80段数据，每段1 000点数据、代表时间2 s，其中临床诊断在105～142 s为发作期，患者表现为双上肢自动症、口咽部自动症；一例28岁颞叶患者(4号)的脑电数据发作间期至发作期200 s，共100段数据，每段1 000点数据、代表时间2 s，其中临床诊断在85～126 s为发作期，患者表现为失神、左上肢自动症、口咽部自动症；一例39岁颞叶患者(5号)的脑电数据发作间期至发作期160 s，共80段数据，每段1 000点数据、代表时间2 s，其中临床诊断在95～116 s为发作期，患者表现为咀嚼、左上肢强直、右上肢自动；一例15岁颞叶患者(6号)的脑电数据发作间期至发作期160 s，共80段数据，每段1 000点数据、代表时间2 s，其中临床诊断在105～136 s为发作期，患者表现为愣神、双上肢自动症。实验采用数据均为头皮脑电数据，采集后由临床脑电图仪进行预处理后存储于医院数据库中，因此可直接将其进行研究。

3.2 实验过程

基于EMD的数据分解及特征值分类、发作预测的过程见图1。对输入信号首先进行EMD分解；对得到各阶的IMF分量进行傅里叶变换从而获得频谱能量；计算特征值，从中选择合适的特征向量作为分类器的输入，进行分类，并对分类器进行参数优化，最后可以得到较为理想的分类结果。

图1基于EMD分解的特征提取及分类优化过程

Fig1EMDdecompositionbasedonfeatureextractionandclassificationoptimizationprocess

首先，利用1号患者的发作间期与发作期各118段数据进行特征提取，将得到的236个样本熵值输入到分类器构建算法中得到分类器。之后将剩余的5位患者脑电数据按顺序各分为两组，输入到构件号的分类器中进行分类，得到分类结果。

3.3 实验结果分析

由于记录数据时数据量较大，因此结合统计学的关联性分析，只选取关联性较小的导联数据进行分析。对6例患者的脑电数据样本进行经验模态分解，并对IMF分量做傅里叶变换，得到频谱，主要频谱能量集中在前三个IMF，因此提取前三个IMF分量的特征值。将已经得到的特征值样本利用CSVM分类器对其进行分类实验，其中核函数为径向基(RBF)函数，惩罚参数取c=1，核函数参数取g=0.01。信号分类实验结果见表1。

通过对训练样本集进行训练，得到分类模型后，利用测试集样本对分类器进行检验，得到的准确率反应了分类器的分类效果，但这种效果只关注了经验风险，因此这种评价有不足之处。为了量化地表示CSVM的学习能力和泛化能力，采取了交叉验证(cross validation，CV)中K-CV的方法对分类器的性能进行验证。K-CV可以有效地避免过学习以及欠学习状态的发生，最后得到的结果也比较具有说服力。

表1 5位受试对象IMF能量谱特征提取方法分类结果

Table1No. 1subjectsoftheIMFenergyspectrumfeatureextractionmethodclassificationresults

数据组测试样本数发作期发作间期正确识别率(%)2号110257691.823号80165791.254号1001862805号801058856号80155486.25

图2 SVC参数寻优

取2号患者数据对分类器的训练情况进行分析。图2是在网格搜索下的参数c和g的不同取值所对应的分类准确率所对应的3D视图及其等高线图。图中x轴表示c取以2为底的对数后的值，y轴表示g取以2为底的对数后的值，等高线表示的取相应的c和g后对应的K-CV方法的准确率，通过图中可以看出把c的范围缩小到2＾(-2)～2＾(4)，同时g的范围可以缩小到2＾(-4)～2＾(4)，这样在上面粗略参数选择的基础上可以再利用SVMForClass进行精细的参数选择。

表3为5位受试者的样本分类效果比较。与经验参数下分类效果进行比较，可以看出在参数优化后，分类器的分类准确率有了明显提高。

表3 受试者脑电数据在两类分类器下的准确率

4 总结与展望

本研究表明，选取EMD对数据进行分解处理时，在一定程度上克服了传统脑电算法处理不具备自适应性信号处理的能力；并针对传统分类算法中假定每个样本的误分类具有同样的代价且每类样本数大致相等的缺陷，提出了代价敏感支持向量机的方法，在分类器进行设计时，考虑样本的不同误分类代价，从而实现代价敏感挖掘；对以构建好的分类器进行参数优化，进一步提高了分类的准确率，较真实地反应了分类器的学习能力和泛化能力。

目前，神经科学的研究已成为生命科学研究的热点。基于非线性动力学的方法，通过对神经电信号的研究，定量描述脑电信号的某些特征，能够对癫痫类神经疾病进行更加深入的探索研究。本研究利用经验模式分解(EMD)在对非平稳时变信号进行多尺度分解，将代价敏感支持向量机运用于癫痫脑电信号的分类，并对分类器进行优化，不仅可以提高临床上癫痫脑电信号的检测与识别的准确率，还可用于实时监测的在线分析，更好地帮助电生理医生客观准确地分析脑电信号，为后续癫痫病的研究提供基础。