基于FPGA的卷积神经网络Softmax层实现

李理，应三丛

（四川大学计算机学院，成都 610041）

基于FPGA的卷积神经网络Softmax层实现

李理，应三丛

（四川大学计算机学院，成都 610041）

FPGA能够充分发挥卷积神经网络的并行特性，并在小尺寸、低功耗的条件下，实现卷积神经网络的运算，是人工智能研究和发展的新方向。其中，Softmax层函数是神经网络的输出层函数，主要用于神经网络的最后一层。首先简要介绍Softmax层函数，分析几种实现函数的方案，然后采用分段拟合的方法在MATLAB上对Softmax层函数进行逼近，对数据进行量化和分析，在FPGA平台用硬件描述语言实现Softmax层函数，并通过Vivado进行仿真，结果表明误差可以控制在较小数量级。

神经网络；FPGA；Softmax；分段拟合

0 引言

神经网络作为机器学习的一个重要领域，随着集成电路的发展，计算机处理能力不断提高，神经网络依然是当今人工智能研究和发展的热点。目前，为了高效地实现对卷积神经网络的计算，多块GPU组成的并行运算平台被广泛运用。然而，由于存在GPU平台体积大、功耗大的特点，小尺寸、低功耗的平台上难以广泛应用卷积神经网络。

FPGA又称现场可编程门阵列，它的特点是能通过硬件编程来实现并行计算。因此，用FPGA来实现神经网络，不仅能大大加快计算速度，降低功耗，同时有助于将神经网络发展到嵌入式领域。

1 Softmax层简介

Softmax函数是神经网络中的一种输出层函数，计算输出层的值，主要用于神经网络最后一层。Softmax定义：

假设有一个数组V，Vi表示V中的第i个元素，∑jej表示从第一个元素值开始的求和，那么这个元素的Softmax值就是：

也就是说，是该元素的自然指数值，与所有元素自然指数值和的比值。由于分母是一个求和，只需要对每一个ei进行分析讨论。下面主要对分子ei进行拟合分析。

本文首先对神经网络中Softmax层定义进行简要介绍，接着提出基于FPGA平台计算的几种方案，并分析各个方案的优缺点，最后采用分段拟合逼近的方法对Softmax进行仿真实现，并对误差进行分析。

2 方案选择

FPGA实现复杂函数计算，目前主要的逼近方法有泰勒展开法、查表法、多项式拟合法、CORDIC算法、分段拟合方法等。

泰勒级数展开的方法需要阶数过多，运算量较大，会消耗FPGA大量乘法器，另外，后面矩阵乘法运算也需要大量乘法器，因此不适合在此处消耗大量乘法器。

查表法是比较直接简单的方法，是将不同自变量对应的函数值事先存入ROM中供查找。优点是适用于任何复杂函数，理论上可以做到无限逼近。另外，这种方法不消耗乘法器，能在一个时钟内出结果。缺点是一旦精度要求高，查找表的尺寸就会增大，消耗存储资源。

多项式拟合非线性函数的时候同样存在需要阶数过高，消耗资源较大的问题，而且计算时间长。

CORDIC算法即坐标旋转数字计算方法，消耗资源较少，但耗时长，同时存在精度不高的问题。

本文采用的是分段函数拟合逼近的方法实现Soft⁃max函数，即在一个范围内将Softmax函数划分为几段，每一段用次数较低的多项式进行拟合的方法。这种方法有着占用资源少，速度较快，精度较高的特点，相对可行。

3 MATLAB拟合及数据分析

用MATLAB内置函数polyfit进行拟合，考虑到计算精度以及计算时间，本文主要对函数ei在（-8,8）区间上分成9个区间段，并设置最高阶数为三次，可以依次得到每一阶的系数。具体各个区间分段及其拟合函数如表1所示。

用MATLAB中的plot等绘图工具，对函数ei，拟合函数，以及两函数差的绝对值，三条曲线进行绘制，得到如图1，图2。

图1为拟合曲线图，可以看出两函数差的绝对值对应的误差曲线基本与x轴重合，直观上精度相对较高，由于图1看不出有三条曲线，图2为拟合曲线和指数曲线部分区域放大的截图。下面输入数据进行分析。

在区间（-8,8）随机取10个数据，取点精度为0.01，得到的拟合值及误差绝对值如表2：

从表可以看出，误差绝对值基本在0.02以下，最大的数值达到0.2，输入值越大，绝对误差会相对大一些，相对误差还是较小的，是由于函数ei图像，随着x值的增大，变化越剧烈造成的。另外，本文考虑到计算的速度时效，采用的拟合最高阶次为3次，如果阶次更高，相对精度也会更高。因此，拟合结果的误差精度是可以接受的。

4 FPGA实现及误差分析

本文使用xc7a35tcpg236-1 FPGA平台去实现ei。

这里使用软件Vivado中的IP核框图调用例化去编程ei的拟合函数y=ax3+bx2+cx+d。首先，建立模块，添加IP Catalog中的 Multiplier和 Adder/Substract⁃er，即乘法器和加法器，进行设置、连线，并添加输入输出。然后，Create HDL Wrapper，添加顶层文件，修改代码进行例化即可完成。

同样的，随机的输入8个x的值。图3为其中一个输入x=7.4的仿真结果图。由于硬件语言限制，不显示小数点，仿真图中第二栏Value的值表示为16位的十六进制，小数点在正中间。

FPGA平台上计算的拟合函数值及误差表见表2。从表2可以看出，绝对误差基本在0.05以内，只有一个误差超出，但是相对误差精度较高，因此误差是可以接受的。

5 结语

本文简要介绍了神经网络系统的Softmax层函数，运用MATLAB采用分段拟合逼近的方法，并在FPGA平台上去实现，对结果进行了误差分析。通过数据分析，误差基本保持在0.05以下，表明该算法可运用在神经网络系统的应用方面，是今后很好的研究方向。

表1 MATLAB分段拟合函数表

图1 MATLAB拟合曲线图

图2 放大截图

图3 仿真结果图

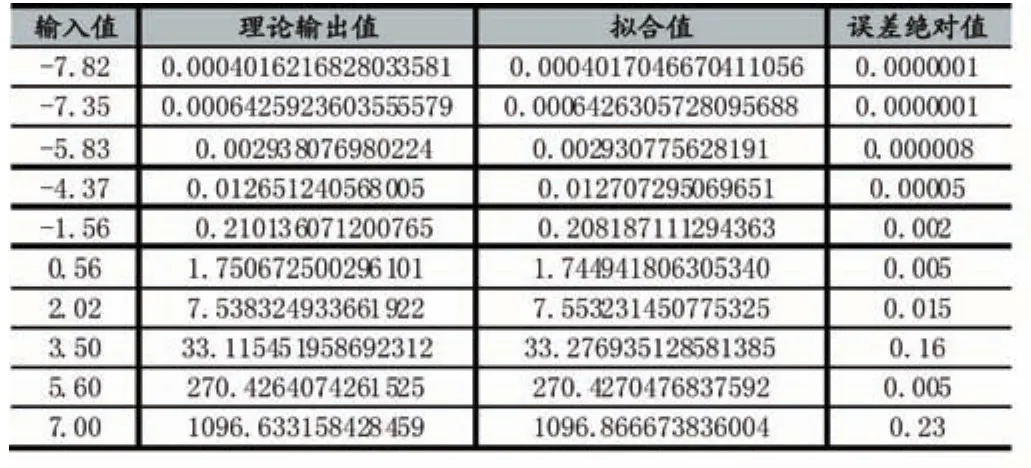
表2 MATLAB拟合函数值及误差表

表3 FPGA上计算的拟合函数值及误差表

[1]张玉玺，刘寒颖，张耀天．基于FPGA的Sigmoid函数实现[J].计算机工程与应用，2016，52（S1）：501-505.

[2]王羽．基于FPGA的卷积神经网络应用研究[D].广州：华南理工大学，2015.

[3]张智明，张仁杰.神经网络激活函数及其导数的FPGA实现[J].现代电子技术，2008（18）：139-142.

[4]陈先昌.基于卷积神经网络的深度学习算法与应用研究[D].杭州：浙江工商大学，2013.

[5]Alin TISAN,Stefan ONIGA,Daniel MIC,Attila BUCHMAN.Digital Implementation of the Sigmoid Function for FPGA Circuits[J]．Electronics and Telecommunications：Volume 50,Number 2,2009：15-19.

[6]王羽.基于FPGA的神经网络硬件实现[D].青岛：中国海洋大学，2008.

[7]刘培龙.基于FPGA的神经网络硬件实现的研究与设计[D].成都：电子科技大学，2012.

Abstract：The FPGA can give full play to the convolution of the neural network parallel features,and under the condition of small size,low power con⁃sumption,realize convolutional neural network arithmetic,is the new direction of artificial intelligence research and development.The Soft⁃max layer function is the output layer function of the neural network,which is used primarily for the last layer of the neural network.Briefly introduces the Softmax layer function principle,analyzes the several functions for realizing scheme,then uses piecewise fitting method in the MATLAB function to approximate the Softmax layer,to quantify the data and analysis,the FPGA platform,uses hardware description language to realize the Softmax layer function and through Vivado simulation,the results show that error can be controlled in smaller orders of magnitude.

Keywords：Neutral Network;FPGA;Softmax;Piecewise Fitting

Softmax Layer Implementation of Neural Network Based on FPGA

LI Li，YING San-cong

（College of Computer Science,Sichuan University，Chengdu 610041）

1007-1423（2017）26-0021-04

10.3969/j.issn.1007-1423.2017.26.005

李理（1990-），男，安徽黄山人，在读硕士研究生，研究方向为集成计算技术实验

2017-06-27

2017-09-10