一种顾及异常控制点的坐标转换方法
2017-10-17谢锋珠王建民
谢锋珠,王 飞,王建民
(1. 山西煤炭职业技术学院,山西 太原 030031;2. 山西能源学院,山西 太原 030060;3. 太原理工大学 矿业工程学院,山西 太原 030024)
0 引 言
随着测绘科学技术的发展,世界上许多国家产生了多个国家坐标系统以及服务于地方的独立坐标系统,我国也不例外。2000国家大地坐标系(China Geodetic Coordinate System 2000,简称CGCS2000)是2008年7月全面启用的新的地心大地坐标系,这就面临着将已有坐标系统下的成果转换到CGCS2000下,其中坐标成果的转换是最为基础的部分,为此,国家测绘地理信息局发布29号公告,要求从2017年3月1日实施大地测量控制点坐标转换技术规范[1]。
坐标转换的精度和可靠性主要取决于转换模型的严密性及其用于求解转换参数的“同名点”的可靠性。通常选择可靠性高的控制点作为同名点用于求解转换参数。控制点本身含有的各种误差会对坐标转换的结果产生影响的问题,文献[2]探讨了随机误差对七参数转换模型的影响:但是由于地壳变形、误差累积或区域性系统误差等因素会导致控制点可能发生了较大的“位移”[3],这种位移量的大小定义为控制点的异常值。如果这种类型的控制点当作同名点求转换参数时,必然会使得转换参数的精度降低,本文将其称作“异常点”。
事实上,坐标转换模型的理论研究和应用较为成熟,大地测量控制点坐标转换技术规范明确指出了常用转换模型及其技术流程[3],其前提条件是同名控制点可靠。然而,在选择同名点的时候,并不能保证同名点绝对可靠,因此,有必要研究在转换过程种探测异常点的坐标转换方法。
在实际应用中,对于异常点的识别主要是计算同名点转换残差是否大于3倍中误差来进行的[4],这类方法对于较大的异常值有效。如果存在多个“异常点”,根据可靠性理论,该方法从理论上来说并不严密,不能有效抵抗多个异常点的影响。
为了提高坐标转换的可靠性,国内外学者将粗差探测理论应用于坐标转换中进行研究。杨元喜将抗差估计理论应用于坐标转换中提高转换参数的可靠性[1],文献[5]系统地分析了13种常用的抗差估计法在坐标转换中抵抗粗差的效力,结果表明调谐系数的大小决定着抗差的效力,虽然每种方法都给出一个调谐系数的经验值,在实际应用中还需要调整,才能取得较理想的效果。
文献[6]提出完整搜索估计法(Full Search Estimation,FSE)定位和估值多维粗差,用于在控制网中探测粗差,后来经过改进和完善FSE并将其应用于坐标转换中,FSE通过粗差对残差影响关系间接地导出了粗差估值方程[8]。本文在FSE形成定位矩阵的基础上,求解粗差的估计,并加以修正,直接评价转换参数的精度。
1 异常点的定位与估值
1.1 异常值的估计
转换参数的求解需要利用两个不同坐标系统下的同名点对当作“观测值”,然后应用最小二乘法(Least Squares,简称LS)求解转换参数。典型的转换模型有布尔莎七参数法[7-8]和平面四参数法[9]。本文以布尔莎七参数模型为例说明异常同名点的定位和估值原理,式(1)为七参数模型。

式中,(xQ,yQ,zQ)为转换后坐标系下的坐标,(xP,yP,zP)为原始坐标系下的坐标;(x0,y0,z0)为3个方向的平移参数,(εx,εy,εz)为3个方向的旋转参数,μ是尺度因子。
使用式(1)至少需要3个非共线同名点对应用最小二乘法求解7个参数,为了提高转换参数求解的精度和定位异常同名点,通常需要增加同名点对的个数。
设两个坐标系统中有k个同名点对,观测值个数n=3k,t=7个未知参数,自由度为r=3k-t。将式(1)的转换模型写成误差方程式(2)的形式,并用矩阵表示为:

式中,R(A)=t,则其解为:

L是由k个同名点对组成的3k×1维向量,如果在坐标系Q或P中存在异常点,则异常点的异常值的大小反映到L中。假设L中受到m个异常点的影响,其大小用m×1维向量ε=[ε1ε2,…,εm]T表示;用n×1维向量ei表示异常位置,且ei=[0,0,…,1,…,0]T(i=1,2,…,n),其中,第j个元素为1表示为异常,其余元素为零,则m个异常点组成n×m矩阵B=[e1e2,…,en],矩阵B称为定位矩阵,此时式(2)进一步改写为[10]:

式中,R(B)=m,n>(t+m),式(4)的LS解为:

根据分块矩阵求逆公式得:


其协因数阵分别为:

由于引入定位矩阵B,由式(4)得到的残差是经过修正后的残差,通过式(7)求解的参数 是经过异常值修正后参数的最佳估值,式(8)得到的ε为异常点中异常值的估计值,式中除了矩阵B以外其他量都为已知量,因此,如何确定矩阵B是关键所在。
1.2 异常点的定位算法
由式(7)和(8)可知,只有确定了异常点的位置,才能估计其大小,借鉴FSE算法的原理并进行简化,设计如下算法步骤生成定位矩阵B。
1)假设有n个同名点对组成L,首先进行LS平差,得到验后方差。
2)暂且认为L中的元素均受到异常点的影响,然后逐个去除Lj(j=1,2,…,n)后,由剩下n-1个元素进行LS平差,可以得到n个对应验后方差(j=1,2,…,n);下标j表示去除第j个元素经LS平差得到的验后方差,在n个验后方差选出其中最小值,并令,定义为n次完整搜索的验后方差,那么Lk对应的同名点对就很有可能包含异常点,并把k的位置写入位置向量ek=[0,0,…,n×1 1,…,1,0]T,1是第k个元素表示异常位置。
3)在L中剩下的n-1个元素中是否受到异常值的影响,继续重复步骤2)进行n-1次完整搜索,需要强调的是每确定一个异常元素Lj后,不再参与后续的LS平差,这样每执行完成步骤2)的搜索后,就会定位一个异常点。
经过以上算法步骤,假设形成了m个位置向量e,并组成了定位矩阵B。
1.3 算法结束的条件
每当执行完成一个完整搜索,就会定位一个异常,假设执行完第m个完整搜索后,正好将全部的异常值搜索完,则。考虑到每一个完整搜索是一个独立的过程,根据F检验原理得:

特殊地,当m=1时,适当地将F值增大,因为此时可能受异常值的影响,相对而言其值会比后续得到的方差较大。显然当ρm>F(f1,f2)时,认为搜索结束,并自动生成定位矩阵B;反之认为无异常。将B分别代入式(7)和(8)得到最佳参数估值和异常值的估计值,用相应的协因数矩阵对其精度加以评价,上述算法的计算流程图如图1所示。

图1 定位、估值计算流程图Fig. 1 Flow diagram of location and estimation
2 算例和分析
算例数据是从CGCS2000坐标系转换到某城市独立坐标系,提供了11个同名点对,其坐标认为无误差,数据见表1。在表中随机选择了4个点模拟了异常值,加粗值为异常值的大小,最大值为5cm,则n=33,t=7,r=26。

表1 同名点对坐标Tab. 1 Coordinates of the corresponding points

表2 异常点定位和估值结果Tab. 2 Location and estimation results of the abnormal points
当搜索结束时,方差比ρm较其他值显著增大。为了突出此特征,如果再进行1次多余的完整搜索,此时的方差比ρm明显回落,如第5次完整搜索后的方差比ρm=1.3。
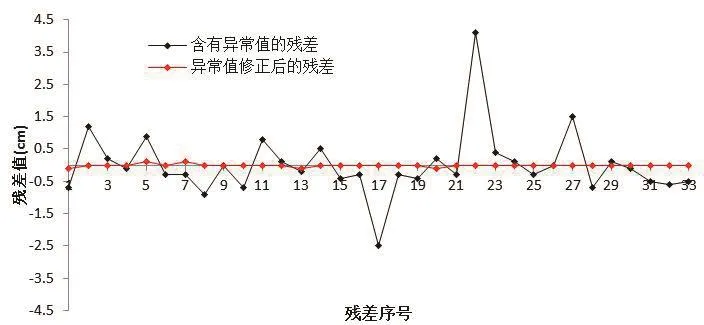
图2 残差对比Fig. 2 Comparison of residual
3 结束语
本文以布尔莎七参数法为例论证了顾及异常点的坐标转换方法,其特点是满足高斯-马尔可夫线性模型国家测绘地理信息局条件的转换模型均适用于该方法。首先通过搜索算法定位异常点,形成定位矩阵,根据F检验原理给出搜索结束的条件,具有理论依据;在求解转换参数的过程中,对异常值加以修正,直接得到参数的最佳估计值。
文中通过一个实例来说明该方法的有效性,结果表明该方法对中小异常值能够定位和估值。其不足之处是估值结果在原坐标系中与其实际异常值的符号正好相反,这是由于原坐标系中的异常值正好以相反的符号转移到目标坐标系中,并不影响转换参数的求解结果。这也说明即使该方法能够估计异常值的大小和符号,但不适合用其直接修正坐标。
