一种风力发电机自动故障诊断及预测方法
2017-10-17向健平姜楠楠SimonJonathanWatson
向健平, 姜楠楠, Simon Jonathan Watson
(1. 长沙理工大学 能源与动力工程学院, 长沙 410114; 2. Faculty of Aerospace Engineering,Delft University of Technology, Kluyverweg 1, 2629 HS, Delft, Netherlands)
一种风力发电机自动故障诊断及预测方法
向健平1, 姜楠楠1, Simon Jonathan Watson2
(1. 长沙理工大学 能源与动力工程学院, 长沙 410114; 2. Faculty of Aerospace Engineering,Delft University of Technology, Kluyverweg 1, 2629 HS, Delft, Netherlands)
为了获得故障信号精确的时域和频域信息,提出了一种Morlet小波变换补偿方法,首先计算出故障信号的时间和频率信息,然后根据Morlet小波系数中心频率峰值对计算的故障信号的幅值进行补偿,得出故障信号的准确幅值.采用Simulink模型证明该方法的可行性,并将该方法应用到测试风力发电机和实际大型风力发电机的电功率信号分析中.结果表明:该方法可以自动获得故障信号按时序排列的振幅趋势图,显示了部件发生故障后的剩余使用寿命期限;风力发电机特别是海上风力发电机的维护维修计划可根据此时间信息进行制定,降低风电运维成本.
风力发电机; 故障诊断; Morlet小波变换; 补偿算法; 电功率信号
Abstract: A Morlet wavelet-based compensated algorithm was proposed to calculate the accurate amplitudes of faulty signals. The specific way is to compute the time range and frequency values of the faulty signals at first, and then to compensate the amplitudes calculated for above faulty signals according to the center frequency values of Morlet wavelet coefficients to further obtain the accurate amplitudes. A Simulink model was used to demonstrate the feasibility and generalization of the algorithm. At the same time, the algorithm was used to analyze the electric power signals of a test rig and large turbines. Results show that this algorithm can automatically find the amplitude trend of faulty components in a time sequence, and indicate the residual service life of wind turbines after faults are generated. Based on the information of the residual service life, the maintenance and repairing plan for wind turbines, especially offshore ones, can be developed to lower the cost of wind power in operation and maintenance.
Key words: wind turbine; fault diagnosis; Morlet wavelet transform; compensated calculation; electric power signal
自然环境中存在很多复杂信号,其中一些如心电图信号和地震信号都是非平稳的,但信号测量方式可以控制[1-2].通常运用小波变换来处理这些复杂的非平稳信号[3].由于这些非平稳信号的频率可通过控制测量方式来确保其信号频率不变,因此,与信号相关物理对象的状态可以通过小波图像比较来监测.然而,还有一些复杂信号,如不可控变工况下的变速异步风力发电机电功率信号中包含的一些元件故障信号,这些信号具有不连续性,其频率随时间发生变化,用传统的小波变换无法有效反映信号的本质特征.这就意味着复杂信号的频率随不可控外界条件的变化而变化,阻碍了传统小波变换的应用.
近年来,随着风力发电机的安装向离岸100 km以外的远海发展,其维护维修更加困难,预测性风力发电机智能化运维研究受到越来越多的重视,因此自动在线状态监控系统和风力发电机剩余使用寿命预测显得更加重要.现有的风力发电机组状态监测主要采用接触式传感器和振动监测设备,以检测轴承、轴和齿轮箱的故障问题,该设备能够在灾难性故障发生之前检测到齿轮箱中的轴承故障.然而,当一个特定的故障即将发生时,单一的系统可能不能给出足够令人信服的证据.欧盟CONMOW项目研究发现,通过一些简单元件测量得到的信号如风力发电机的输出功率信号,能够用Morlet小波变换补偿方法计算出一些故障的信号及其能量发展趋势,判断出这些故障在不同阶段的故障程度,因而有可能实现自动在线状态监控和相关元件剩余使用寿命的预测,即Morlet小波变换补偿方法可从电功率信号中分离出相关故障信号,然后按时间序列来比较相关故障信号的能量趋势,若故障信号的能量趋势上升,则表明该元件存在故障且其故障程度在加深.
综上所述,将Morlet小波变换补偿方法应用于风力发电机电功率信号的分析,有可能实现对一些元件的状态监测和剩余使用寿命预测.新的Morlet小波变换补偿方法兼顾了快速傅里叶变换(FFT)和传统Morlet小波变换的优点,既可以从复杂信号中提取非平稳信号,又可以计算对应频率的信号幅值.
笔者首先从理论上进行讨论,然后应用Simulink仿真来分析如何从一个复杂信号中提取非平稳信号的幅值信息.同样用Simulink仿真模型对比了FFT和传统Morlet小波变换的不足之处,并通过25 kW小型风力发电机的实验对结果进行验证.
1 Morlet小波变换补偿方法
研究Morlet小波变换补偿方法是为了解决工程实际中出现的一些问题.如图1中,风力发电机电功率信号中的与其主轴故障相关的2sf1非平稳信号[4]频率,随风力发电机主轴速度(受风速影响)的变化而变化,因s是包含了风力发电机转轴转速的转差率,所以故障信号的频率也将随不可控的风力发电机转速的变化而变化.此外图1也表明电功率信号中还包含了许多故障相关频率成分[5],如三叶片旋转频率和两倍滑差频率.笔者因此提出了一种分析此类复杂信号的新算法——Morlet小波变换补偿方法[6],探讨该算法在风力发电机电功率信号分析中的应用,实现对一些元件的状态监控和剩余使用寿命的预测.这种方法已成功应用于一些变速风力发电机中[7].
图1展示了传统Morlet小波变换能够从电功率信号中提取出2sf1信号,但用传统Morlet小波变换计算信号幅值时,计算值随频率变化而变化,这使得信号振幅不能确定,因而无法直观观察故障随时间的变化情况[8-11].
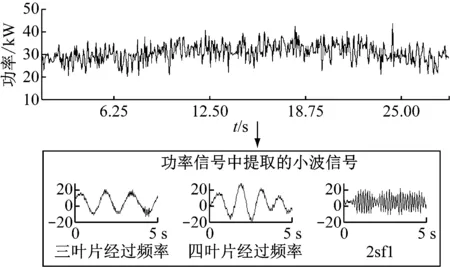
图1 风力发电机电功率信号和Morlet小波变换提取的叶片旋转频率和滑差调制振动信号
Fig.1 Power signal from a wind turbine and Morlet-wavelet transform of the passing frequencies and the slip modulated vibration signal
Morlet小波变换补偿方法是建立在传统小波分析法基础上,因此这里先讨论连续小波变换,然后根据拉普拉斯变换卷积定理推导出Morlet小波变换补偿方法.
1.1 连续小波变换
连续小波变换的定义为:
(1)
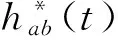
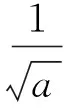
(2)
由于小波随时间轴变换,式(1)可以用变量t替换参数b,用变量τ来替换t:
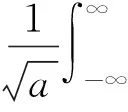
(3)
式(3)也可以用相关运算符⊗和卷积运算符*表达如下:
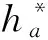
(4)
其中,
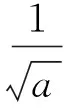
(5)
从图形角度来说,2个信号的卷积就是将一个信号进行翻转、平移,再乘以另一个信号.相关性只涉及到移位和相乘(不涉及翻转),是用来衡量2个信号的相似性.因此,可以利用多个波形之间的交叉相关性来检测特定频率的周期信号.
式(4)表明,Ws(a,t)是由信号s(t)映射到小波ha(t)上得到的,是一组离散序列的小波系数,信号s(t)的时间和频率信息由与其具有极高相似性的小波ha(t)揭示,但信号的振幅却没有显示.为了确定信号的幅值信息,有必要做一个信号幅值与小波变换系数之间的解映射.接下来详细介绍Morlet小波变换的基本理论并推导Morlet小波变换补偿方法.
1.2 Morlet小波变换
为便于计算和仿真,采用Matlab软件进行计算.Matlab中Morlet母波表达式如下:
h(t)=e-t2/2cos(5t)
(6)
根据式(2)可以得到子波表达式:
(7)
显然,在时域范围内,当a>1时,子波是母波的扩张波;当a<1时,子波是母波的压缩波.利用Matlab中的Morlet小波变换可以获得一系列小波系数.图2中的波形表明小波系数是一个时间长度为2 s,频率为5 Hz的正弦信号,该小波系数频率在小波变换的中心频率5 Hz处幅值最大.除中心频率外的波形的幅值明显不同于原始正弦信号的幅值,下面从理论上推导如何得到Morlet小波变换补偿方法,并计算图2中单频正弦信号s(t)的幅值.
根据拉普拉斯变换卷积定理,2个原函数的卷积的傅里叶变换等于2个原函数傅里叶变换的乘积,式(1)中小波变换的傅里叶变换表达式[12-13]可写成:
Ws(a,ω)=S(ω)Ha(ω)
(8)
式中:Ws(a,ω)、S(ω)和Ha(ω)分别为Ws(a,t)、s(t)和ha(t)的傅里叶变换.
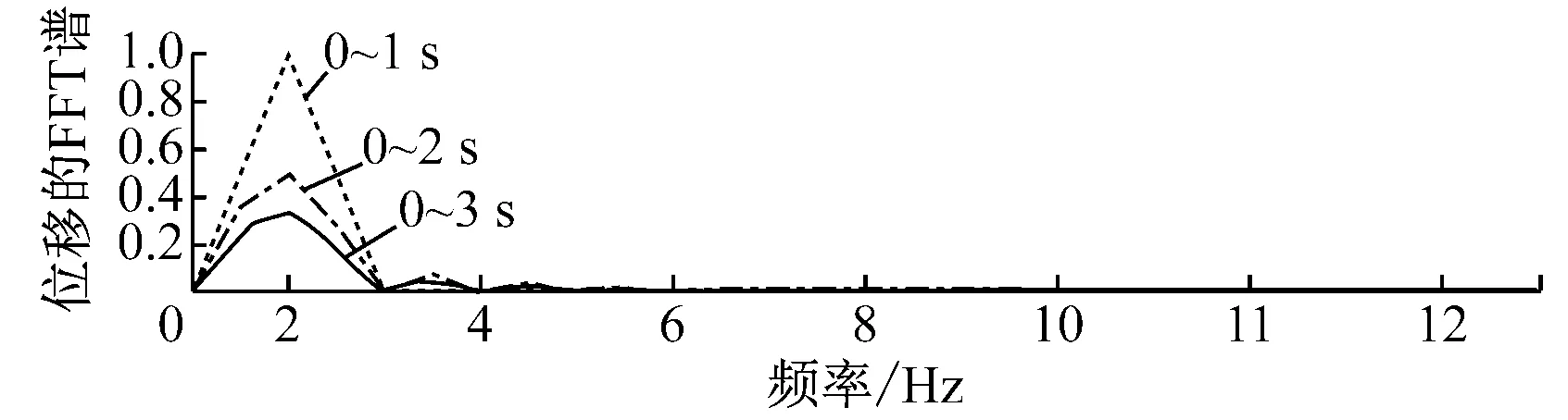
Morlet小波是对称分布的,在中心频率处形成带通滤波.当小波ha(t)的中心频率与信号s(t)频率相等时,小波系数Ws(a,ω)具有最大幅值,即相关性最高.图3(a)给出了时间长度为5 s的单频正弦信号取不同频率时得到的Morlet小波系数的傅里叶变换图谱.由图3(a)可知,带宽随着中心频率的增加而增加,且振幅随着中心频率的增加而减小.由于信号时间长度为5 s的傅里叶变换的频率分辨率为0.2 Hz,所以频率为2.1 Hz和2.3 Hz和2.5 Hz处的振幅是由傅里叶变换窗泄露引起的.因此,得到小波系数与信号振幅间的关系显得尤为重要.
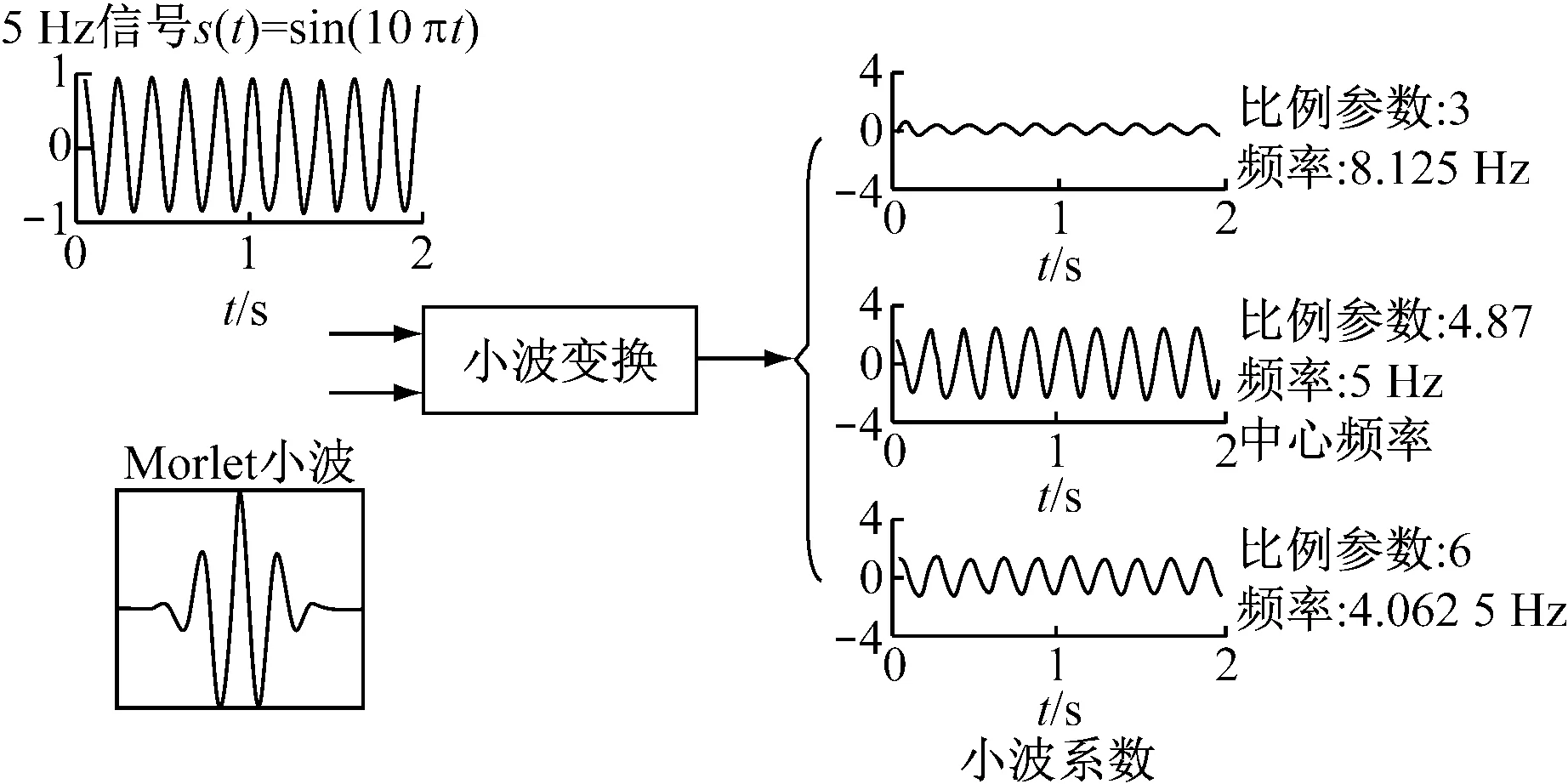
图2 单频正弦信号的小波系数
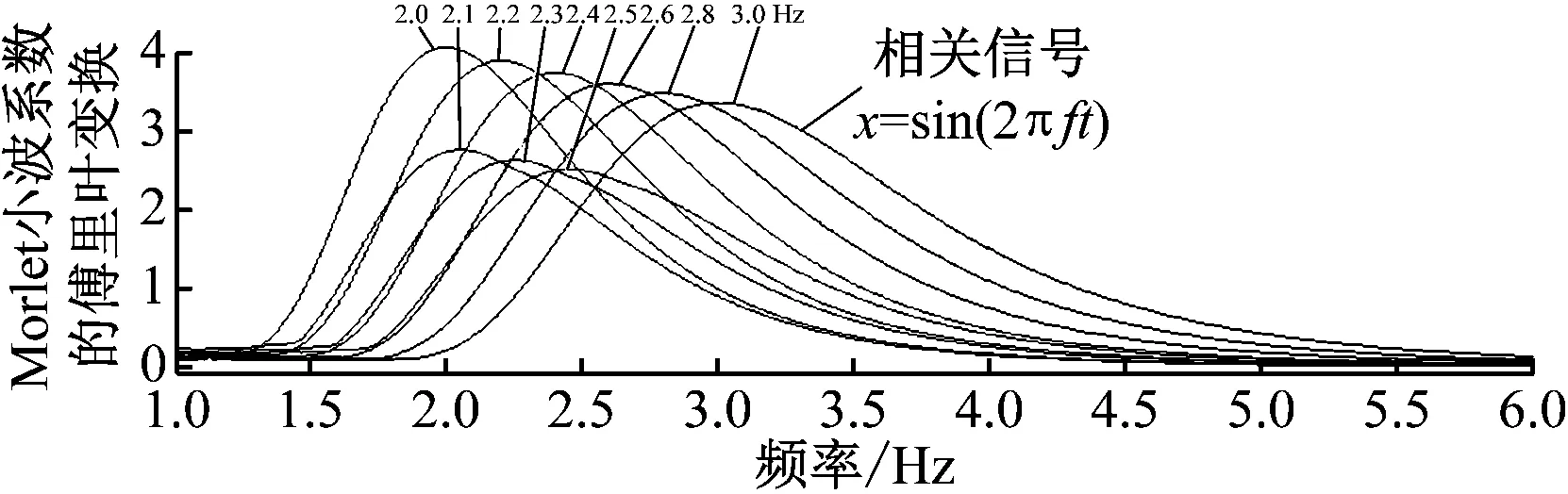
(a) Morlet小波系数的傅里叶变换
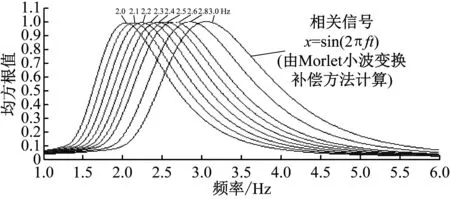
(b) 补偿后Morlet小波系数的均方根值
1.3 补偿后信号振幅的计算
传统Morlet小波变换在中心频率处的振幅误差修正如下.
对式(5)应用尺度定理可得:
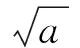
(9)
式中:H(ω)为h(t)的傅里叶变换.
文献[14]中给出了Morlet小波的傅里叶变换:

(10)
根据式(5)、式(9)和式(10)得到的Morlet小波的傅里叶变换如下:
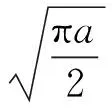
(11)
由于f=ω/2π,式(11)表明Morlet小波在频域范围内是以fcenter=5/(2πa)为中心的带通滤波器.
用频率f代替角频率ω,则Morlet小波在频域的傅里叶变换为:
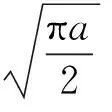
(12)
从式(12)可以看出,若补偿能够实现,则频率成分能够通过计算中心频率处Morlet小波系数得到.
由式(12)可推导出式(13):
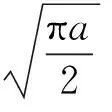
(13)
式中:f0为中心频率.
对一个频率为f0的正弦信号来说,中心频率处的小波变换为:
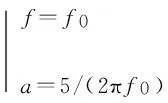
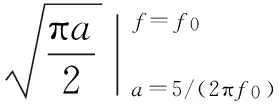
(14)
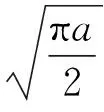
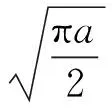
(15)
将式(15)命名为Morlet小波变换补偿方法,因为传统Morlet小波变换的信号幅值得到了补偿.图3(b)为单频正弦信号x=sin(2πft)取不同频率时经新算法补偿之后的小波系数图,为避免快速傅里叶变换的频率分辨率问题,使用均方根值代替快速傅里叶变换幅值来计算小波系数的幅值.其中,均方根值反映了信号的能量,对于一个正弦波,其均方根值约为其峰值的0.707倍.显然,无论信号频率取值如何,中心频率的幅值与原始正弦信号的幅值始终相等,具体可由式(13)确定.
传统Morlet小波变换能够从复杂信号中提取非平稳信号,而推导出来的新算法能够获得非平稳信号的幅值,因此复杂信号的非平稳频率成分的幅值能够通过Morlet小波变换补偿方法计算得到.
Morlet小波变换补偿方法的特点有:能确定非平稳信号的幅值和频率,这对分析一些高度复杂的数据序列尤其重要,如变速风力发电机电功率信号中由故障元件引起的非平稳故障信号.利用Morlet小波变换补偿方法和智能计算机工程,能够建立复杂系统的在线自动监测系统,如风力发电机在线自动监测系统.
2 Simulink振动信号仿真
风力发电机传动系统中叶片、传动轴和齿轮箱等部件与发电机转轴相联,若这些部件发生故障,其引起的非平稳振动信号将通过风力发电机气隙磁场的作用,叠加到风力发电机电功率信号中.首先需要了解振动机制,由于轴承故障和终端三相故障较为广泛[15-18],因此用一个Simulink模型产生非平稳振动信号,并说明在线自动监测系统的工作过程.
由于简谐力作用下的球轴承振动特性具有典型性,其径向振动可以通过二阶微分方程来描述,本节将说明如何用Simulink模型对机械振动系统及其故障产生的非平稳信号进行仿真,并利用Simulink模型得出的结果,解释Morlet小波变换补偿方法的相关问题.
为简单起见,以式(16)的常系数二阶微分系统为例:

(16)
若设f(t)为二阶常微分系统的脉冲激振力,式(16)的单位脉冲响应函数为:
(17)
系统的非阻尼固有频率为:

(18)
式中:M为质量系数;B为阻尼系数;K为刚度系数;A为振幅;φ为相位角.
若暂时施加一个冲击作用力f(t),则振动会在几个周期后消失.振动的自然频率和下降速度取决于系统参数K、M和B.如果在短周期内间歇性施加冲击作用力,将出现振幅变化连续的振动信号.
图4给出了一个有确定参数的二阶微分方程的Simulink模型,用来模拟间歇性施加冲击作用力引起的振动.相关Simulink模型如下:

(19)
此处B=10 N·m/s,M=1 kg,K=298.51 N/m,式(19)为一个单位脉冲函数.
系统无阻尼自然频率为:
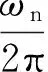
(20)
实际情况下,由于部件与部件之间的接触点不同,故障元件引起的振动信号也有所不同.图4(b)模拟了一个因为故障产生的变化的冲击作用力,图4(c)表明所导致的振动信号也不规则.
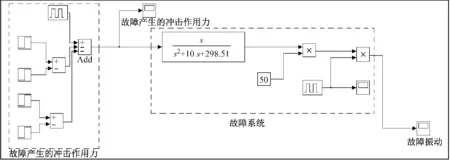
(a) Simulink模型
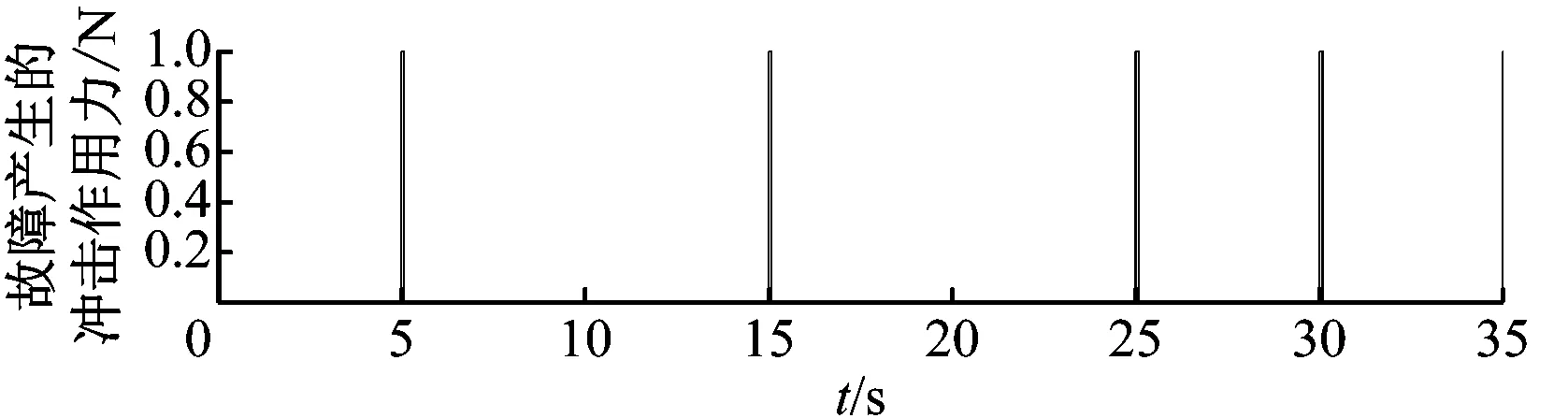
(b) 仿真故障产生的冲击作用力
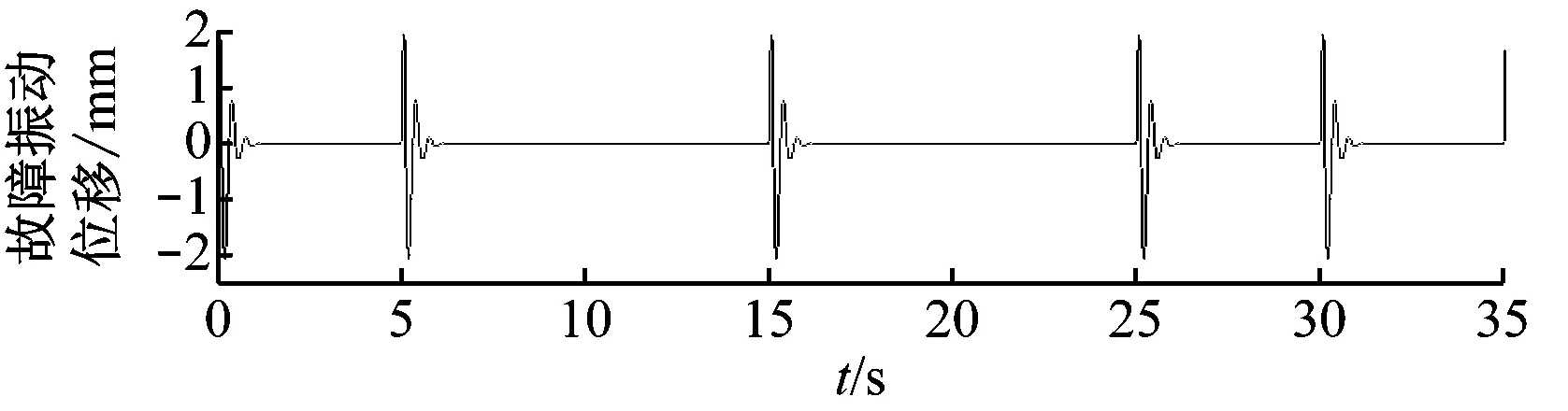
(c) 故障振动信号
3 利用Morlet小波变换补偿方法监测振动程度
图5(a)给出了一个时间长度为1 s,频率为2 Hz正弦信号的非平稳信号.图5(b)为图5(a)的快速傅里叶变换,显然,两信号之间的时间间隔越长,FFT计算的幅值将会越小.由图5(a)可知,在对信号进行FFT之前,时域信息对于非平稳信号至关重要,这项工作可通过小波变换实现.
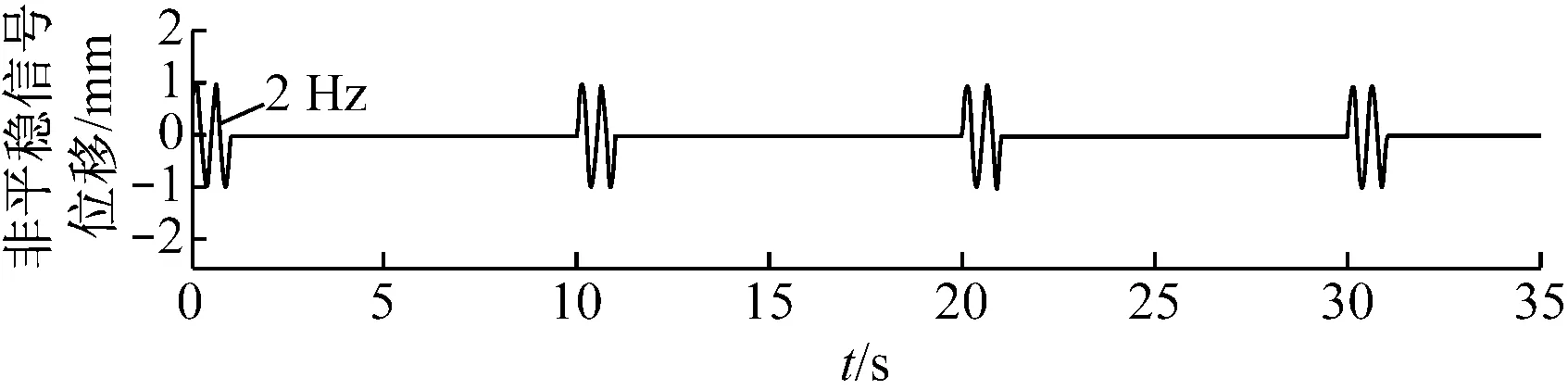
(a) 非平稳信号(2 Hz)
(b) (a)的快速傅里叶变换
图6(a)给出了一个复杂信号,包含一个由式(20)决定的非平稳振动信号和一个50 Hz的正弦信号.其振动信号小波如图6(b)所示.
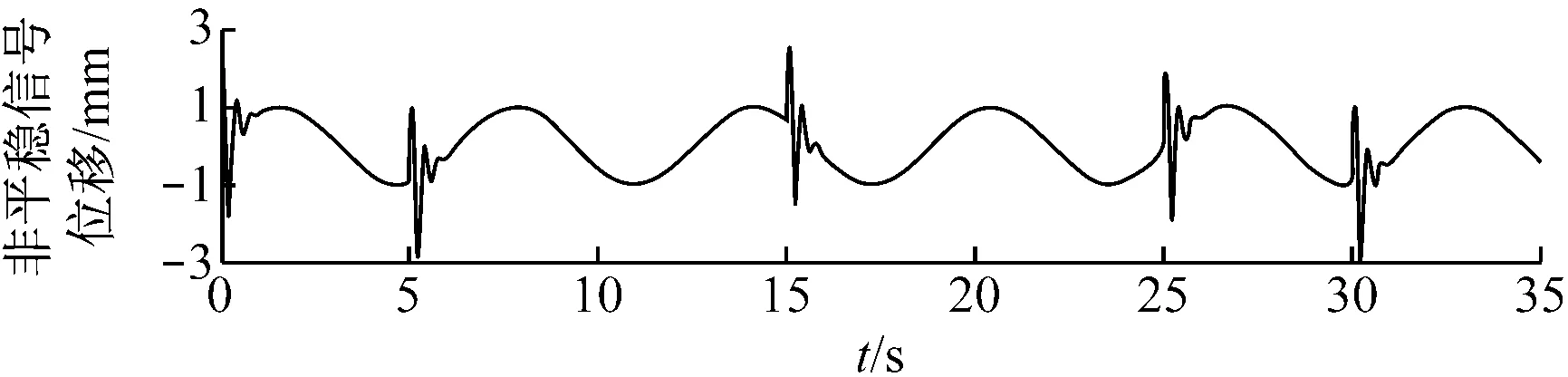
(a) 振动信号加一个50 Hz的正弦信号
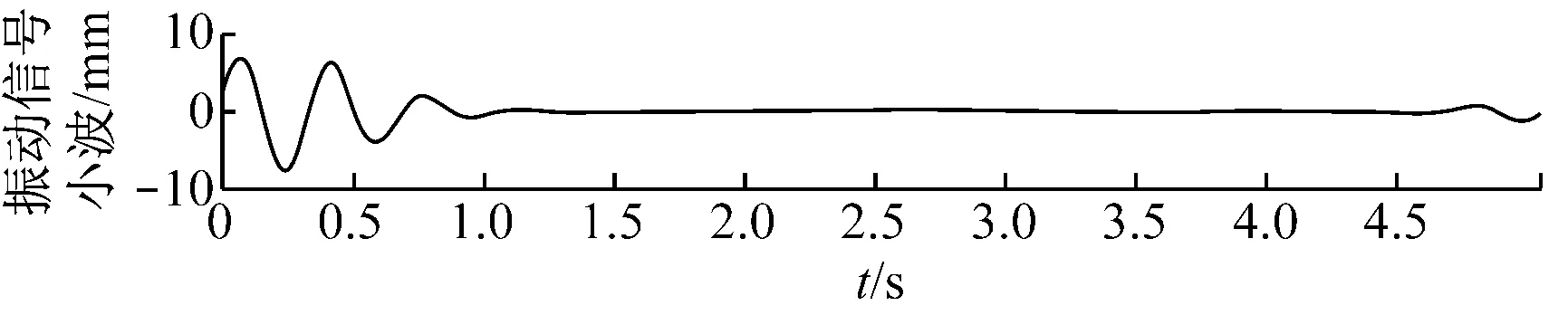
(b) 从(a)中提取的振动信号小波
图7(a)是以1 s为时间长度的振动仿真信号,利用FFT计算其振幅频谱图得到图7(b),图7(c)为仿真信号的小波变换系数,图7(d)为Morlet小波变换补偿方法计算图7(c)得到的振动仿真信号频谱图.显然,利用FFT计算的图7(b)与利用Morlet小波变换补偿方法得到的图7(d)的结果相似,进一步说明Morlet小波变换补偿方法能确定非平稳信号的幅值和频率.
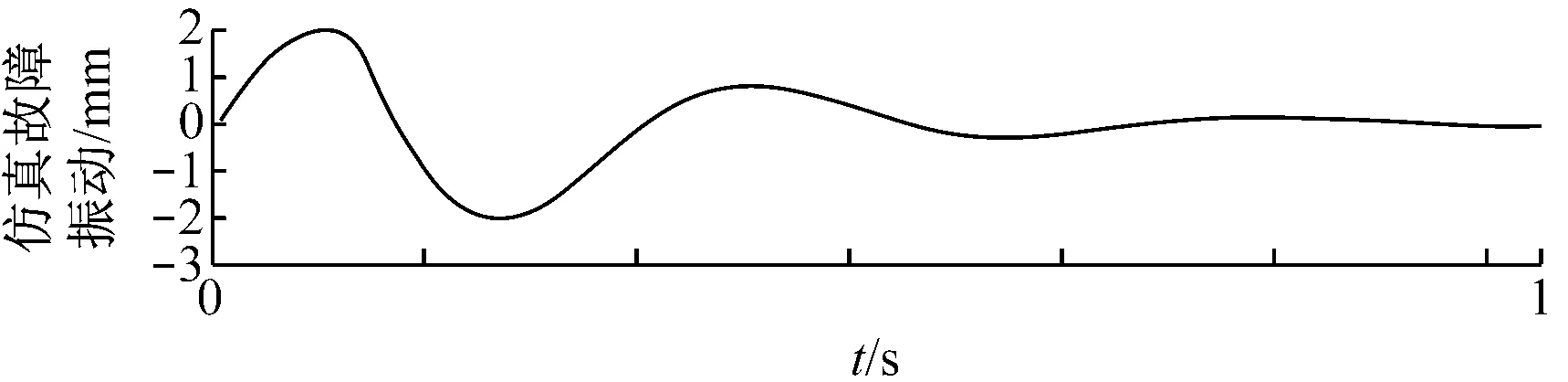
(a) 振动仿真信号

(b) 仿真信号的傅里叶变换

(c) 仿真信号的小波变换系数

(d) Morlet小波变换补偿方法计算(c)得到的谱图
当元件故障更加严重时,振动幅值会增加,这种情况下,采用一个自动的故障诊断方法来计算振幅趋势尤为重要.图8(a)和图8(b)是由Simulink模型产生的与图4(a)信号相似的信号.图8(c)是基于新算法所计算的振幅谱,每个信号段振幅计算取决于一个合理的时间长度,显然Morlet小波变换补偿方法能够检测图8(b)中信号的幅值变化.图8(a)模拟主轴偏心产生故障时对主轴产生的冲击作用力.设5 s、15 s和20 s处故障产生的作用力大小为1 N;在25 s和30 s处故障产生的作用力大小为2 N,依次仿真风速变化时的风力机主轴偏心故障产生的冲击作用力.图8(b)的仿真结果表示主轴产生故障时主轴承产生的振动信号振幅能够通过Morlet小波变换补偿方法计算.在实际复杂环境下,如近海风力机状态监控中,可以每天、每时甚至每秒计算信号振幅趋势,见图8(c).
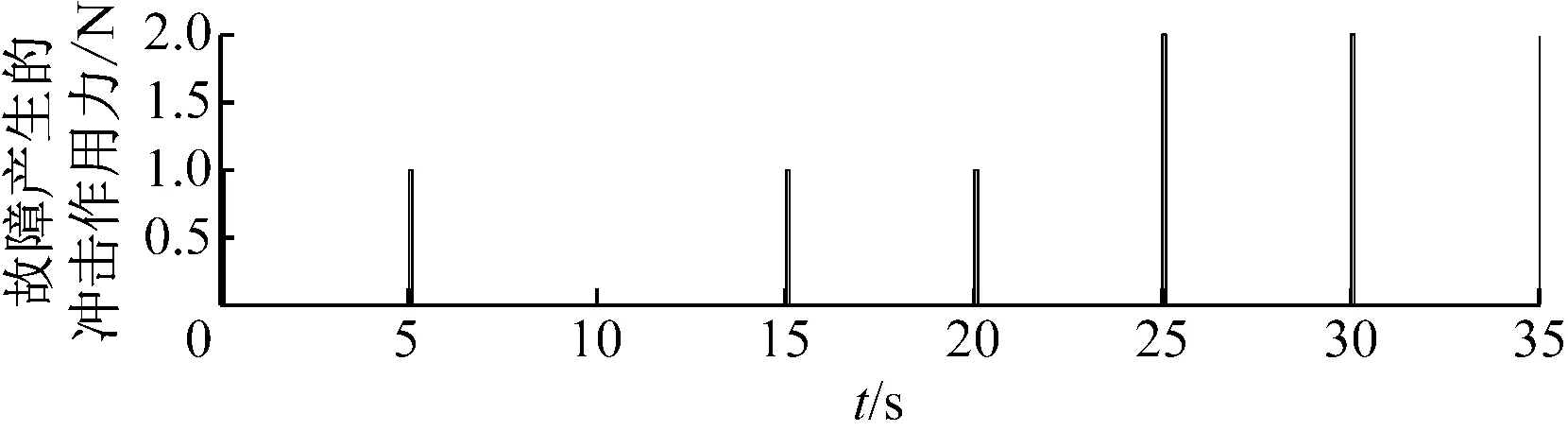
(a) Simulink模型仿真故障产生的冲击作用力

(b) Simulink模型产生的故障信号
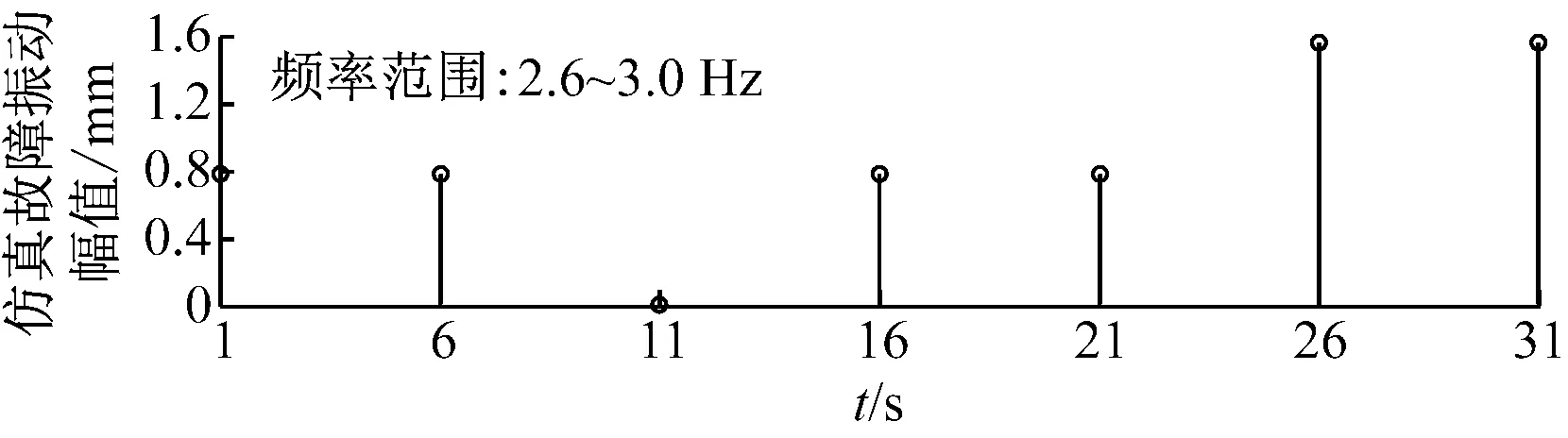
(c) 故障信号小波的振幅
4 Morlet 小波变换补偿方法的应用
由于耦合在风力发电机轴上的任何故障元件所引起的振动是通过气隙作用于磁感应强度的,也就是说,故障元件的频率将反映在磁感应强度中,因此也将反映于电流、转矩和电功率信号中.同样,一个异步电机,主轴转速与同步转速不等,转差率s将调制一些故障相关的振动信号,如s/2可能是由主轴不平衡或电流不平衡引起的.为了确定实际情况下Morlet小波变换补偿方法的可行性,将这种方法应用于2台25 kW的小型风力发电机上进行验证.
图9给出了故障信号断续施加在25 kW小型风力发电机上的结果.从图9(a)可以看出,与正常情况下相比,当电流不平衡时,两倍滑差频率的振幅变大.从图9(b)可以看出,质量不平衡所导致的两倍滑差振幅更大,同样证明了振动变化是风力发电机典型不平衡问题的特征.图9(b)中,振动随时间变化而周期变化,振动信号的长度和大小与系统参数、两部分的接触位置、故障分量的受力等相关.然而,当施加不平衡质量后振幅会增加.不平衡越严重,振动越明显.
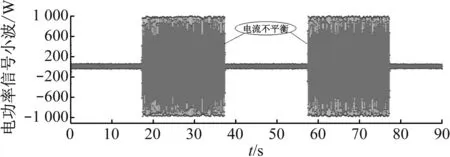
(a) 频率为17.99 Hz的电功率信号小波幅值

(b) 频率为8.74 Hz的电功率信号小波
图10为利用电压信号传感器和加速度传感器对25 kW小型风力发电机的传动系统状态进行分析对比的实验结果.图10(a)和图10(b)表明两者的故障信息非常相似.
图11中,2010年6月25 kW小型风力发电机传动系统失效前两天其振动信号与从风力发电机电信号计算出的故障幅值均急剧增加,进一步说明Morlet小波变换补偿方法可用来预测风力发电机相关部件的剩余使用寿命.从图11可以看出,故障信号振幅比正常时的幅值高出几倍,风力发电机监测程序应该发出风力发电机部件严重损坏的警告.
然而,笔者认为利用实际风力发电机的数据获得的剩余使用寿命预测方法,在经济上是不可取的.该方法还需结合理论计算或实验方法,获得变风速情况下故障信号不同幅值之间进行比较和校正.在运行中,滚过受损轴承部件会产生特定的振动频率,若完全损坏时的振动强度能通过理论计算或实验确定,就可将Morlet小波变换补偿方法计算得出的振动强度与完全损坏时的振动强度进行比较,结合计算得出的振动强度变化速度,应可估计出距离轴承完全损坏导致风机停止运行的时间长度.风力发电机特别是海上风力发电机的维护维修计划,将可根据此时间长度信息制定,降低风电运维成本.由于理论计算或实验方法需要更深入的研究,将在今后工作中作进一步讨论.
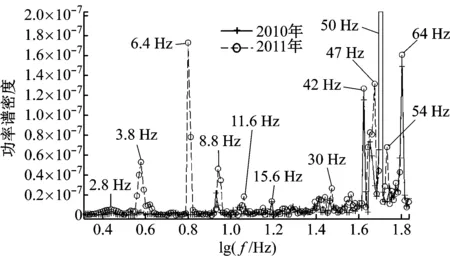
(a) 加速度传感器信号频谱
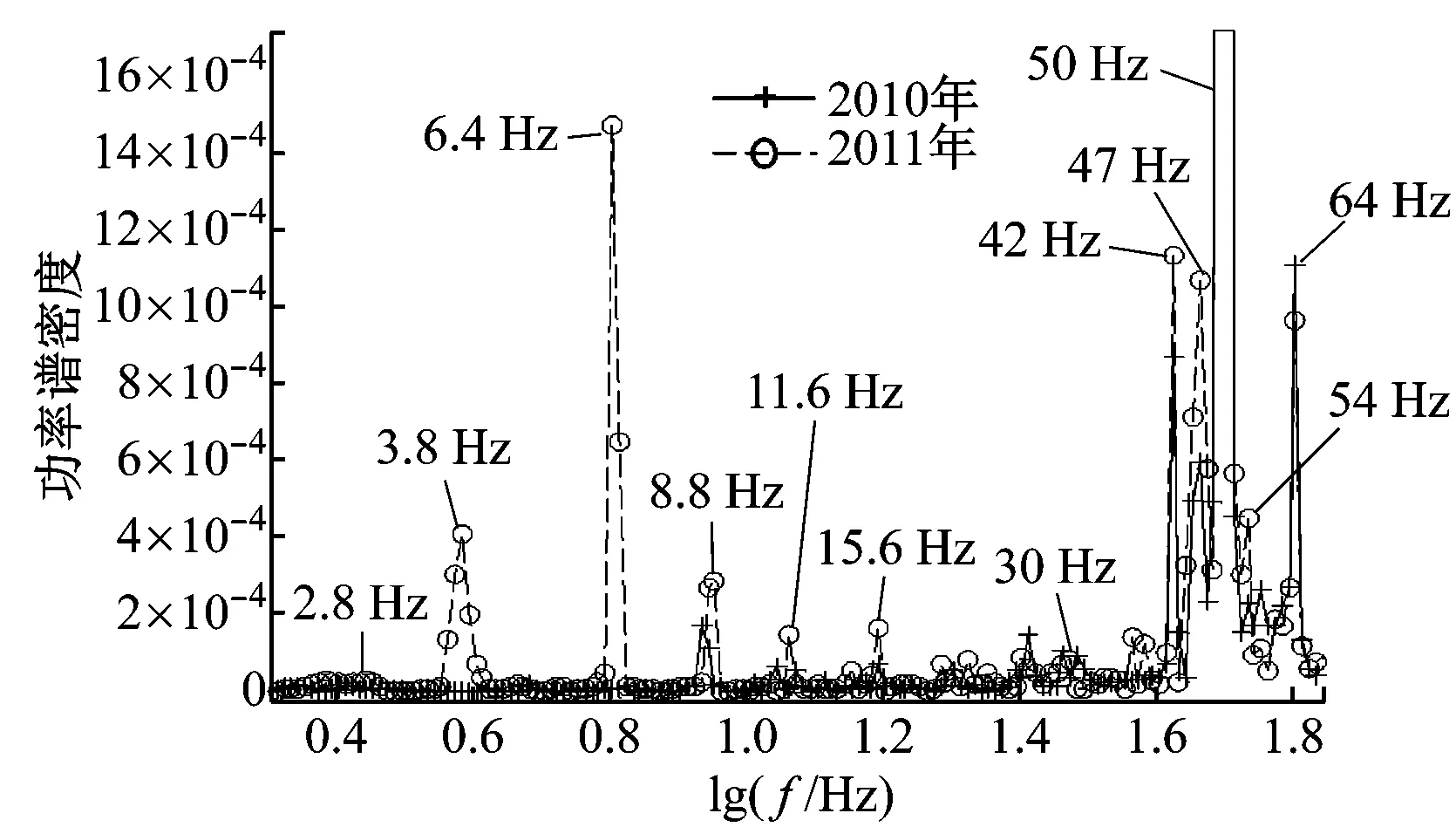
(b) 电压信号频谱
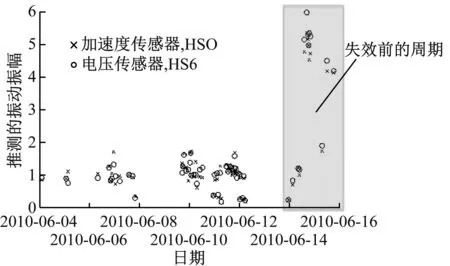
图11 25 kW小型风力发电机传动系统故障振幅图
5 结 论
所采用的Morlet小波变换补偿方法能较准确地计算非平稳信号的振幅和频率.将Morlet小波变换补偿方法应用到风力发电系统故障诊断和状态监测时,无需增添额外的测量装置,因此降低了系统的成本.仿真结果表明,采用Morlet小波变换补偿方法分析电功率信号来检测故障与利用振动信号分析的结果基本相同.将Morlet小波变换补偿方法应用于测试风力发电机和实际大型风力发电机上的结果都表明了该新方法的有效性.基于该新方法的风力发电机状态监测系统将有可能对一些部件的剩余使用寿命进行预测.
[1] ADDISON P S. Wavelet transforms and the ECG: a review[J].PhysiologicalMeasurement, 2005, 26(5): 155-199.
[2] 祁浩, 王福豹, 邓宏. 基于无线传感器网络的地震信号特征提取方法研究[J].物理学报, 2013, 62(10): 104301.
QI Hao, WANG Fubao, DENG Hong. A novel approach to research on feature extraction of seismic wave signal based on wireless sensor networks[J].ActaPhysicaSinica, 2013, 62(10): 104301.
[3] ROCHA M P C, LEITE L W B. Treatment of geophysical data as a non-stationary process[J].Computational&AppliedMathematics, 2003, 22(2): 149-166.
[4] 向玲, 李媛媛. 经验小波变换在旋转机械故障诊断中的应用[J].动力工程学报, 2015, 35(12): 975-981.
XIANG Ling, LI Yuanyuan. Application of empirical wavelet transform in fault diagnosis of rotary mechanisms[J].JournalofChineseSocietyofPowerEngineering, 2015, 35(12): 975-981.
[5] VAS P. Parameter estimation, condition monitoring, and diagnosis of electrical machines[M]. Oxford, UK: Clarendon Press, 1993.
[6] WIGGELINKHUIZEN E, VERBRUGGEN T, BRAAM H, et al. Assessment of condition monitoring techniques for offshore wind farms[J].JournalofSolarEnergyEngineering, 2008, 130(3): 031004.
[7] WATSON S J, XIANG J. Real-time condition monitoring of offshore wind turbines[C]//ProceedingsofEuropeanWindEnergyConference&Exhibition(EWEC). Greece:EWEA publication, 2006: 647-654.
[8] 耿宇斌, 赵学智. 基于Morlet小波变换与SVD的故障特征提取[J].华南理工大学学报(自然科学版), 2014(7): 55-61.
GENG Yubin, ZHAO Xuezhi. Fault feature extraction based on Morlet wavelet transform and singular value decomposition[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2014(7): 55-61.
[9] TSE N C F, LAI L L. Wavelet-based algorithm for signal analysis[J].EURASIPJournalonAdvancesinSignalProcessing, 2007,2007: 1-10.
[10] WATSON S J, XIANG B J, YANG W X, et al. Condition monitoring of the power output of wind turbine generators using wavelets[J].IEEETransactionsonEnergyConversion, 2010, 25(3): 715-721.
[11] 程发斌, 汤宝平, 赵玲. 最优Morlet小波滤波及其在机械故障特征分析中的应用[J].中国机械工程, 2008, 19(12): 1437-1441.
CHENG Fabin, TANG Baoping, ZHAO Ling. A filtering method based on optimal Morlet wavelet and its application in machine fault feature analysis[J].ChinaMechanicalEngineering, 2008, 19(12): 1437-1441.
[12] XIONG Y G, QUEK F. Gestural hand motion oscillation and symmetries for multimodal discourse: detection and analysis[C]//IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition. Madison, Wisconsin, USA: IEEE, 2003.
[13] KELLEY N D, OSGOOD R M, BIALASIEWICZ J T, et al. Using time-frequency and wavelet analysis to assess turbulence/rotor interactions[C]//19thAmericanSocietyofMechanicalEngineers(ASME)WindEnergySymposium. Reno, NV, USA: ASME, 2000: 130-149.
[14] SHYU H C, SUN Y S. Construction of a Morlet wavelet power spectrum[J].MultidimensionalSystemsandSignalProcessing, 2002, 13(1): 101-111.
[15] CHENG J S, YU D J, YANG Y. Application of an impulse response wavelet to fault diagnosis of rolling bearings[J].MechanicalSystemsandSignalProcessing, 2007, 21(2): 920-929.
[16] 胡爱军, 马万里, 唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报, 2012, 32(11): 106-111.
HU Aijun, MA Wanli, TANG Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J].ProceedingsoftheCSEE, 2012, 32(11): 106-111.
[17] 卢绪祥, 苏一鸣, 吴家腾, 等. 基于EMD及灰色关联度的滑动轴承润滑状态故障诊断研究[J].动力工程学报, 2016, 36(1): 42-47.
LU Xuxiang, SU Yiming, WU Jiateng, et al. Fault diagnosis on lubrication state of journal bearings based on EMD and grey relational degree[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(1): 42-47.
[18] 安学利, 蒋东翔, 李少华. 基于决策融合的直驱风力发电机组轴承故障诊断[J].电网技术, 2011, 35(7): 36-41.
AN Xueli, JIANG Dongxiang, LI Shaohua. Fault diagnosis of spherical roller bearing of direct-drive wind turbine based on decision fusion[J].PowerSystemTechnology, 2011, 35(7): 36-41.
Automatic Fault Diagnosis and Prediction of Wind Turbines
XIANGJianping1,JIANGNannan1,SimonJonathanWatson2
(1. School of Energy and Power Engineering, Changsha University of Science and Technology,Changsha 410114, China; 2. Faculty of Aerospace Engineering, Delft University of Technology,Kluyverweg 1, 2629 HS, Delft, Netherlands)
2016-08-22
2016-10-03
湖南省长沙市科技局科技计划资助项目(k1508017-11)
向健平(1959-),女,湖南衡阳人,教授,博士,研究方向为风力发电机故障诊断、状态监控和寿命预测. 电话(Tel.):18670734190; E-mail:beth.j.xiang@qq.com.
1674-7607(2017)10-0821-08
TM315
A
480.60
