风力机翼型动态失速的数值模拟

宗涛

（湖北能源集团鄂州发电有限公司，湖北 鄂州 436032）

风力机翼型动态失速的数值模拟

宗涛

（湖北能源集团鄂州发电有限公司，湖北 鄂州 436032）

利用计算流体力学软件FLUENT，对二维翼型NACA23012在非定常流动中的动态失速进行数值模拟研究，分析了翼型在振荡周期内升力系数随攻角的变化，并进一步研究了俯仰运动的几个关键参数对翼型动态失速的影响，得出了翼型升力系数循环曲线在不同攻角、不同振幅、不同衰减频率下的变化规律，并与实验结果相比较。

翼型；动态失速；迟滞效应；数值模拟

0 引言

动态失速是指一个振荡（或做其他非定常运动）的压力面在超过其临界迎角时绕流流场发生非定常分离和失速的现象。对于风力机翼型来说，在大攻角、低雷诺数来流的工况下，当翼型产生振颤时极易出现动态失速现象。当风轮处于失速状态运行时，最大输出功率和最大叶片载荷将会同时出现，而目前不计失速影响的理论计算载荷只有实测值的50%-70%。失速风轮在高风速下所产生的这种很大输出功率可能引起发电机的损坏，因此，在设计时必须认真考虑动态失速的作用。近年来，许多学者针对这一问题进行了大量的研究[1-3]，如刘雄[4]等人通过实验初步分析了NACA4415翼型的动态气动特性，陈旭[5]等人对NREL s809翼型的二维动态流场进行了数值模拟等。本文应用CFD软件FLUENT对二维翼型NACA23012的动态失速现象进行数值模拟。

1 计算网格及边界条件

对数值模拟流场进行网格划分是求解控制方程的基础，网格质量的好坏将直接影响数值计算的结果，而网格的生成关键在于网格点的合理分布。基于不同的网格生成方法，可使用结构化和非结构化网格来离散计算域。本文采用非结构化网格，并采用局部加密的方法，图1所示为网格的局部放大图。网格点在翼型前缘分布较密，整个流场计算域的网格数为69 380个。

图1 网格分布图Fig.1 Grid profile

动态失速中一个关键的问题是翼型在流场中发生了振荡运动，因此，翼型振荡运动的形式对流场的变化起着关键性作用。研究表明，风力机叶片发生的振颤可认为是按照正弦规律变化的运动。当叶片发生振荡时，其截面翼型与流场中来流的相对方位是随时间不断变化的，这个变化所引起的主要影响是来流对翼型的攻角也产生周期性的振荡变化。由流场运动的相对性，可以设翼型振荡运动过程中其攻角的变化形式为α=α0+Δα⋅sin(ω⋅t)，其中α0为平均攻角，Δα为振幅。取翼型的振荡轴心为弦长的四分之一处。边界条件设为无穷远压力边界，空气视为理想气体，雷诺数Re=1.5×106，计算采用k-ω SST模式。

2 结果分析

2.1 模拟值与实验值比较

文献[6]给出了翼型NACA23012静态时、绕振荡轴心规律振荡时升力系数（翼型所受到的升力与气流动压和参考面积的乘积之比）随攻角变化的实验值。图2所示为静态时升力系数随攻角的变化。由图知，升力系数随攻角的增加，先增加后减小，失速攻角在15°左右，升力系数峰值约为1.3。在实验条件与数值模拟条件一致的情况下，模拟值与实验测得的结果吻合。

图2 静态时升力系数随来流攻角的变化Fig.2 Lift coefficient with flow static angle of attack

图3 振荡翼型升力系数随来流攻角的变化Fig.3 Variation of lift coefficient of oscillating airfoil with inflow angle of attack

图4 不同攻角下翼型周围速度矢量图Fig.3 Velocity vector around an airfoil at different angles of attack

图3所示为翼型俯仰振荡时升力系数随攻角的变化，图4为不同攻角下翼型周围速度矢量图。采用的数值计算条件为：自由来流Ma=0.12，衰减频率，其中c为弦长，U∞为远场来流速度；平均攻角α0=15°，振幅Δα=10°。由图易知，振荡上仰阶段升力系数随着攻角的增加而增加，当上仰至最大值时，翼型向下振荡，此时升力系数急速下降，而后有小幅上升。1点为失速延迟点，由于翼型的振荡作用延迟了失速现象的发生，甚至不发生失速，使得升力系数峰值远大于静态时峰值，几乎为静态时峰值的2倍；当翼型上仰至2点时，发生前缘分离，使升力系数明显增加。随着攻角的进一步增加，主分离涡的位置升高，向后缘移动，并在前缘和后缘诱导出二次分离涡；进入下俯过程以后，后缘的分离涡变大，并和主分离涡一起脱离翼型表面，此时翼型上方的涡为前缘诱导出的二次涡，当下俯至4点时该二次涡到达翼型尾缘，并随着翼型的下俯振荡逐渐脱离翼型表面；当下俯至5点时，翼型表面的流动又恢复为附着流动。模拟值与实验所得结果变化趋势一致，但具体值存在有差异，迟滞环小于实验所得结果，数值精度的不足和湍流模式的缺陷是造成这一差异的主要原因，尤其是湍流模式方面[7]。同时上述数值模拟所选择的雷诺数Re、衰减频率k的取值与实际工况相符。

2.2 迟滞效应的影响因素

从俯仰运动的数学表达式可知：简谐俯仰运动的几个关键参数为振幅Δα，振荡角频ω，平均攻角α0，以及俯仰运动的扭转点位置。如果气动计算条件不变，则俯仰运动的迟滞效应由这几个参数决定[8]。

2.2.1 平均攻角的影响

数值计算条件为：自由来流Ma=0.12，衰减频率k=0.10，振幅Δα=10°，取平均攻角分别为6°、12°、20°，如图5-图7所示。

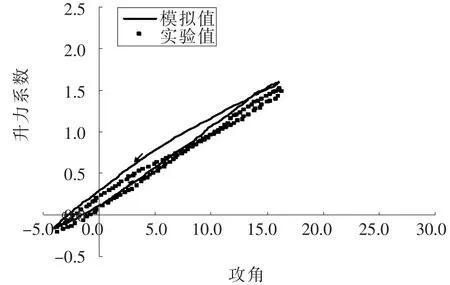
图5 平均攻角为6°时振荡翼型升力系数随攻角的变化Fig.5 The lift coefficient of oscillating airfoil varies with angle of attack when the mean angle of attack is 6°

图6 平均攻角为12°时振荡翼型升力系数随攻角的变化Fig.6 The lift coefficient of oscillating airfoil varies with angle of attack when the mean angle of attack is 12°

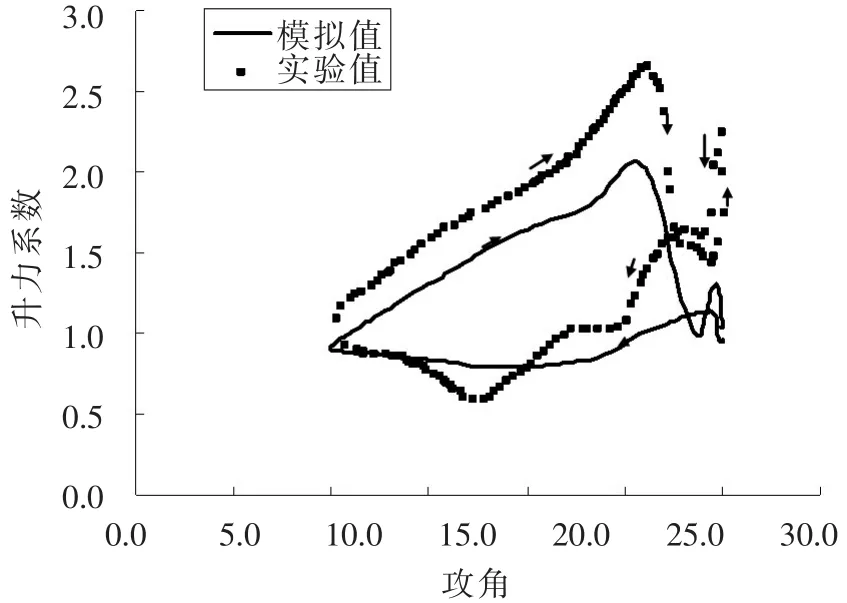
图7 平均攻角为20°时振荡翼型升力系数随攻角的变化Fig.7 The lift coefficient of oscillating airfoil varies with angle of attack when the mean angle of attack is 20°

从图5-图7可见，当平均攻角最小时，流体几乎附着在翼型附近流动，升力系数曲线为特殊的椭圆形。当平均攻角为12°时，出现动态失速，由实验值知直到翼型下俯至4°时升力系数又恢复为附着流动时的值，这表明了下俯振荡延迟了流动恢复为附着流动的过程。当平均攻角为20°时，最大升力系数几乎是静态时升力系数峰值的2倍，在上仰阶段，升力曲线斜率呈现比较大的非线性变化。失速攻角在25°左右，升力系数达到峰值后，先下降后又升高，再次出现峰值。二次峰值的出现和二次涡的形成有关。模拟所得结果与实验结果变化趋势一致，具体值存在有一定差异，模拟所得迟滞效应没有实验结果明显。

2.2.2 振幅的影响

数值计算条件为：自由来流Ma=0.12，衰减频率k=0.10，平均攻角α0=18°，取振幅分别为2°、6°、10°，如图8-图10所示。

图8 振幅为2°时振荡翼型升力系数随攻角的变化Fig.8 The lift coefficient of oscillating airfoil varies with angle of attack when the amplitude is 2°

图9 振幅为6°时振荡翼型升力系数随攻角的变化Fig.9 The lift coefficient of oscillating airfoil varies with angle of attack when the amplitude is 6°

图10 振幅为10°时振荡翼型升力系数随攻角的变化Fig.10 The lift coefficient of oscillating airfoil varies with angle of attack when the amplitude is 10°

从图7-图9可见，当振幅为2°时，翼型完全失速；当振幅为6°时，动态失速圆环曲线再次出现，此时出现轻失速现象，失速由后缘分离引起；当振幅为10°时，迟滞效应更加明显，发生深失速现象，上仰阶段发生前缘分离，升力系数明显增加。上仰过程模拟结果与实验结果变化趋势较吻合，下俯过程差异较大。

2.2.3 衰减频率的影响

数值计算条件为：自由来流Ma=0.12，平均攻角α0=10°，振幅Δα=10°，取衰减频率分别为0.10、0.16、0.20，如图11-图13所示。

图11 衰减频率为0.10时翼型升力系数随攻角的变化Fig.11 Variation of lift coefficient of airfoil with angle of attack when attenuation frequency is 0.10

图12 衰减频率为0.16时翼型升力系数随攻角的变化Fig.12 Variation of lift coefficient of airfoil with angle of attack when attenuation frequency is 0.16

图13 衰减频率为0.20时翼型升力系数随攻角的变化Fig.13 Variation of lift coefficient of airfoil with angle of attack when attenuation frequency is 0.20

从图11-图13可见，当衰减频率为0.1时，典型的动态失速圆环曲线即已出现。随着衰减频率的增加，循环曲线变窄，迟滞效应越来越不明显，流动分离现象出现延迟，失速攻角增加，上仰过程模拟结果与实验结果吻合较好。

3 结论

通过对以上动态失速现象的数值模拟，可以看出：

（1）翼型发生动态失速时，其升力系数峰值大于静态时升力系数峰值，失速造成风力机实际输出功率大于理论计算值。

（2）翼型俯仰振动的几个关键参数对动态失速有很大的影响，平均攻角较小时，流体几乎附着在翼型附近流动，迟滞环不明显。

（3）振幅越大，动态失速越明显，振幅较小时失速多为轻失速，由后缘分离引起；振幅较大时失速多为深失速，首先形成很大的前缘分离涡，该分离涡在翼型表面运动诱发出二次流动，引起升力系数的显著变化。

（4）衰减频率的大小决定了翼型振荡角频的大小，衰减频率较小时失速延迟现象明显。

模拟值较准确地计算了升力系数迟滞曲线的变化趋势，基本趋势与实验结果较符合，但在具体值上与实测值还存在有一定的差异。

（References）

[1]尚丽娜，夏品奇.可变翼型动态失速气动模型研究[J].中国科学:技术科学，2015,(09):975-983.Shang Lina，Xia Pingqi.Study of aerodynamic model for morphing airfoils in dynamic stall[J].Scientia Sinica(Technologica),2015,(09):975-983.

[2]B.Stoevesandt,Joachim Peinke,A.Shishkin,Claus Wag⁃ner.Numerical Simulation of Dynamic Stall using Spectral/hp Method[M].Wind Energy,2004.

[3]O.Frederich,U.Bunge,C.Mockett,F.Thiele.FlowPre⁃diction Around an Oscillating NACA0012 Airfoil at Re= 1,000,000[M],IUTAM Bookseries,IUTAM Symposium on‘Unsteady Separated Flows and their Control’,Corfu,Greece,18-22 June 2007.

[4]刘雄，梁湿，陈严等.风力机翼型动态失速气动特性仿真[J].工程力学,2015,(03):203-211.Liu Xiong，Liang Xiang，Chen Yan,et al.Dynamic stallsimulation ofwind turbine airfoils[J].Engi⁃neering Mechanics,2015,(03):203-211.

[5]陈旭，郝辉，田杰等.水平轴风力机翼型动态失速特性的数值研究[J].太阳能学报,2003,24(6):735-740.Chen Xu，Hao Hui，Tian Jie,et al.Investigation on airfoil dynamic stall of horizontal axis wind turbine [J].Acta Energiae Solaris Sinica,2003,24(6):735-740.

[6]J.G.Leishman.Dynamic stall experiment on the NACA23012 aerofoil[J].Experiments in Fluids,1990, 9(1-2):49-58.

[7]钱炜祺，符松，蔡金狮等.翼型动态失速的数值研究[J].空气动力学学报，2001,19(4):427-433.Qian Weiqi,Fu song,Cai Jinshi,et al.Numerical study of airfoil dynamic stall[J].Acta Aerodynamica Sinica,2001,19(4):427-433.

[8]张正秋，邹正平，刘火星等.振荡翼型非定常流动数值模拟研究[J].燃气涡轮试验与研究，2009,22(3):1-8.Zhang Zhengqiu,Zhou Zhengping,Liu Huoxing,et al.Numerical Study of Two Dimensional Flow on an Oscillating Airfoil[J].Gas Turbine Experiment and Research,2009,22(3):1-8.

Numerical Simulation of Airfoil Dynamic Stall of Wind Turbine

ZONG Tao
（Hubei Energy Group Ezhou Power Generation Company Limited，Ezhou Hubei436032，China）

In this paper,the dynamic stall of the 2-d airfoil NACA23012 is simulated by using the computational fluid mechanics software FLUENT,the change of lift coefficient with power An⁃gle in the oscillating cycle is analyzed,and the influence of several key parameters of pitch motion on the dynamic stall of airfoil is studied.The variation rules of the cyclic curve of the wing lift co⁃efficient in different Angle,amplitude and attenuation frequency are obtained and compared with the experimental results.

airfoil;dynamic stall;hysteresis effect;numerical simulation

TK83

B

1006-3986(2017)04-0050-05

2017-02-21

宗 涛(1986),男,湖北武汉人，硕士，工程师。

10.19308/j.hep.2017.04.011