数学复习课——知识生长的摇篮

王春梅

（江苏省宿迁市沭阳如东实验学校）

数学复习课
——知识生长的摇篮

王春梅

（江苏省宿迁市沭阳如东实验学校）

在培养学生核心素养的视域下，强调知识、能力与态度的统整.数学复习课堂应成为数学知识生长的摇篮，即让基础概念自然生长、核心知识整合生长、基本经验自然增长、学习方式自然延伸，让数学复习课成为学生知识生长的摇篮、培养学生核心素养的沃土.

自然生长；整合生长；自然增长；自然延伸

当前，在培养学生核心素养的视域下，从三维目标到核心素养的改变，更为强调知识、能力与态度的统整.因此，当前的教学改革与实践需要聚焦学习本源，反映学科本质，重构教学价值.数学复习教学，不是已有知识的简单重复，而是引领学生在已有知识的基础上，站在新的起点上，系统回顾知识，综合运用所学知识，感悟数学思想，建构知识的内在体系.让基础概念自然生长、核心知识整合生长、基本经验自然增长、学习方式自然延伸，从而让学生在数学复习中学会学习，学会成长.让数学复习课成为学生知识生长的摇篮、培养学生核心素养的沃土.

一、前沿后续，让基础概念自然生长

好的教育应该让学生听到知识“自由生长”的声音.在复习课中，不是已有基础概念的简单呈现，教师应当引导学生在对相关概念要点已有理解的基础上，自主尝试定义；依据知识要点，自主设计题目；注重问题设计，建立知识内在联系，让学生在学习中实现基础知识的无缝对接，自然生长.

例如，在复习“方程”章节中，根据方程的定义组织学生自主尝试定义一元一次方程、一元二次方程、二元一次方程，理解定义中“元”与“次”的本质及内涵；再引导学生根据一元一次方程的相关考点自主设计一元二次方程、二元一次方程的相关题目；设计内在联系紧密的问题串，强化建立知识的内在联系.例如，2x-y=1是二元一次方程，这个方程有无数组解，如……若通过变形可写成y=2x-1的形式，即为我们所认识的什么内容？一次函数.这些解可以看作什么？直线y=2x-1上的点的坐标.因此，对于二元一次方程可以生长出我们所学过的哪些内容？通过问题引领，让学生体验、建构数学基本概念之间的内在联系，使得概念之树自然生长.

二、润物无声，让核心知识整合生长

在初中数学知识体系中，数学核心知识处于核心地位，在背景材料、数学思想等方面包含了丰富的数学学科思想观念，自我生长和迁移能力强，是保持教学内容逻辑连贯的重要纽带.在数学复习课中，加强数学核心知识教学，有利于把握数学学习的整体性和连贯性，架设数学学科知识之间的桥梁，完善学生数学学科的核心观念，建立数学学科观念.

首先，数学复习课应进一步理清核心知识的内涵和外延、在不同学段的呈现形式、变式联系，以核心知识为中心发散，为学生提供通性、通法的思维方式和解题策略，从而使学生从整体上掌握基于核心知识的层次结构和纵、横联系，形成以核心知识为生长点的认知结构，体验数学知识的连贯性和整体性，提高学生的数学认识和数学核心观念.

其次，数学复习课应以提升学生的数学素养为目标，深入挖掘核心知识所蕴涵的数学思想方法与核心观念，突出重点、难点和关键点，关注典型结构特征及体现通性、通法的解题策略的数学问题，关注学生平时出现的典型错误，指导学生纠错，引导学生究错，促使学生在自主整理和综合应用的过程中对所学知识进行精致加工，系统整合，完善认知结构，领悟数学思想方法的一致性，形成逻辑连贯的思维方式和问题解决能力的认识论和方法论.

例如，在复习作辅助线构造三角形全等时，如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF=90°，且EF交正方形外角的平分线CF于点F.

（1）如图1，若E是边BC的中点，M是边AB的中点，连接EM.求证：AE=EF.

（2）如图2，若点E在线段BC上滑动（不与点B，C重合）.在点E滑动的过程中，AE=EF是否一定成立？试说明理由.

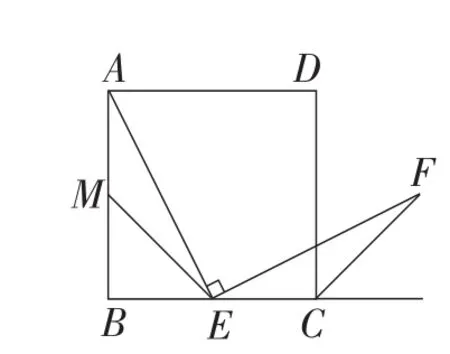
图1

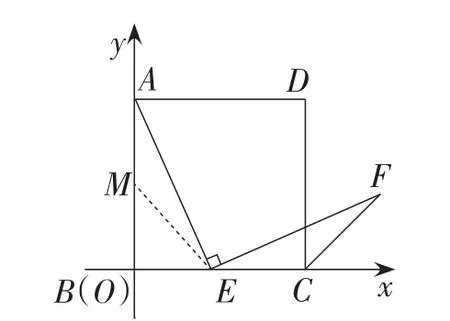
图2

第（1）小题利用△AME≌△ECF证得AE=EF，第（2）小题中如何证明AE=EF？学生直觉感知应该过点F作FH垂直x轴，垂足为点H，但是此时无法证明构造的△EFH与△AEO全等.在这样的情况下，应有效地“疏”，应启发学生在思维受阻时该如何及时调整思路，从第（1）小题中找启发，在AB上截取BM=BE，构造△AME≌△ECF，做到顺势而行、自然而为.

三、化零为整，让基本经验自然增长

学生的学习需要从“经历”走向“经验”.数学复习，应从一节一节的碎片教学中跳出来，应以“主题（单元）”作为进行教学的基本思考对象，如复习中常常将“函数”作为教学设计单元；也可以以数学中的重要主题为教学设计单元，如“最值问题”或“方案设计与实践操作”等；也可以将通性、通法的数学内容作为设计单元，如“全等与相似模型”等.单元复习时，教师应当引领学生不断激活、更新和丰富已有的基本生活经验与数学现实，并且通过前引后连、前呼后应进行强化与优化，实现基本经验在复习过程中的自然生长，实现新、旧经验与数学现实的衍生增长.例如，“函数”的复习内容，其中函数的增减性是一难点.对于一次函数y=kx+b（k，b为常数，k≠0），可以从数形结合的角度在直角坐标系内依据直线的上升或下降的认知经验来认识其增减性.在此经验之上，如何总结、归纳反比例函数（k为常数，且k≠0）的增减性？从反比例函数的图象发现双曲线不是连续的，分布在第一、三象限或第二、四象限，所以反比例函数的增减性应该强调在每个象限内，同样依据此经验可以概括出二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）的增减性应强调对称轴左、右两侧.

四、善用类比，让学习方式自然延伸

“类比”是一种探究式思维方法，是根据不同事物在某些特性上的相似，推理出它们在另一些特性上也可能相似的思维形式.在数学复习课中，通过类比，激活知识结构的联结点，搭建新、旧知识的思维联系，触类旁通，自然延伸思维方式与学习方式，促进知识的有效迁移.

1.在类比中深化理解

在数学复习中，有很多知识之间存在着某些相似或相同点.复习过程中实时地类比学习内容之间的某些共性、差异和特殊性，深化理解知识，使知识系统化，实现知识的意义建构.

例如，在复习“数与式”一章时，从整式与分式的判别入手，下列代数式中哪些是整式，哪些是分式？-2x2，，-3xy+2xy2，发现其中既不是整式也不是分式，那属于哪一种代数式呢？问题引导学生主动分析，类比整式与分式，我们应该从哪几个方面掌握二次根式？并类比对整式与分式的学习，从性质、相关概念、运算等方面对二次根式进行复习.

2.在类比中解决问题

问题解决是以已有的知识经验为基础，如果缺乏足够的先前知识，问题则无法得以顺利解决.即使所谓的“新问题”，也能在贮存的知识系统和方法结果中提取某些相关“原型”，解决问题的关键是能否从已有的知识储备中顺利提取到相关信息.类比能将新问题转化为已有知识经验中相似的问题原型，通过比较在两者之间建立联系，实现知识的有效“迁移”，把当前的情境转换为熟悉的、简单的、清晰的情境，从而使问题得到解决.运用类比的方式，使复习成为基本自主建构概念及相关知识点实现知识迁移和能力提升的过程.复习中学生能类比正方形中含45°特殊角时旋转构造全等得出含60°特殊角时的情形，使相关问题得以轻松解决，这就是数学学习最大的收获.

数学是思维的科学，数学教学是思维的教学.数学复习课中，要在学生已有知识和认知水平的基础上学会发现、学会探究、学会创造，使已有知识得以自然生长，枝繁叶茂.

［1］杨九诠.学生发展核心素养三十人谈［M］.上海：华东师范大学出版社，2017.

［2］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2017—07—16

王春梅（1976—），女，中学高级教师，江苏省特级教师，江苏省教学名师，江苏省“333”工程高层次人才培养对象，江苏省乡村数学骨干教师培育站负责人，主要从事课堂教学及数学学习心理研究.