算术编码算法在图像压缩中的研究∗

吴晓云

算术编码算法在图像压缩中的研究∗

吴晓云

（商洛学院电子信息与电气工程学院 商洛 726000）

算术编码是一种无损的数据压缩方法，可以极大地减小信号的冗余度，由于其比较高的压缩效率使得它被广泛地应用在图像压缩中。论文首先对算术编码算法、编码过程以及有限精度推导过程进行了研究，最后在Matlab对算术编码的静态模型和自适应模型进行了仿真和分析。结果显示算术编码压缩效果良好，能实现图像数据的无损压缩，体现了算术编码图像压缩上的优良性。

无损压缩；算术编码；静态模型；自适应模型

AbstractArithmetic coding is a lossless data compression method，which can greatly reduce the redundancy of the signal.Be⁃cause of its high compression efficiency，it is widely used in image compression.The arithmetic coding algorithm，the coding pro⁃cess and the finite precision derivation process is studied in this paper.Finally，the static model and the adaptive model of arithme⁃tic coding are simulated and analyzed in Matlab.The results show that the arithmetic coding has a good compression effect.It can re⁃alize the lossless compression of image data，and it shows the good performance of arithmetic coding image compression.

Key Wordslossless compression，arithmetic coding，static model，adaptive model

Class NumberTP391

1 引言

在进入信息化时代之后，各种数据量剧增，数据压缩技术的研究受到越来越多的重视。算术编码是一种无损压缩方法，有着非常好的压缩性能［1］。由于计算机硬件及精度过长等方面的限制，算术编码在压缩领域没有得到很好的应用。但是随着对算术编码理论研究的成熟和压缩技术的改进，算术编码作为一种优于其它熵编码方法，将成为图像数据压缩方法的主要编码方法，应用在图像视频压缩领域。

2 算数编码的基本算法

2.1 算数编码原理

假设符号序列为［00，01，10，11］，它们的概率分布p（00）=0.1，p（01）=0.4，p（10）=0.2，p（11）=0.3，对输入10001100101101序列进行编码，编码过程可以如下［2］：

1）对信源符号按照概率的大小排列，将最开始的区间设置为当前区间。信源符号在当前区间所占的大小与它的概率成正比。

2）选择第一个信源符号，找到这个符号在当前区间的比例间隔，将此比例间隔作为新的当前区间。这个区间的上下限就成为新区间的上下限，最后把当前区间的起点指示的数加到编码输出数。

3）再次按照信源符号的概率序列在新区间划分比例间隔。然后选择下一个信源符号，重复第二步。直到输入完信源序列，最后的输出就是其算术编码。具体如图1所示。

图1 算术编码过程

由图1可以看出其算术编码的最后输出在0.5143876～0.514402之间。可以在此区间内任意选择一个小数作为编码的结果，比如0.5143878。

算术编码的优良性众所周知，但是算术编码有一个最大的缺点就是：随着对信源序列编码的逐渐进行，小数点后的位数会逐渐增加，而很多计算机的精度不能无限增加［3］。比如16位、32位或者64位，那么溢出就不可避免，精度的限制就成了必不可少的一部分，所以在描述区间的小数上提出了有限精度描述。

2.2 有限精度描述与推导

1）精度描述［4～5］

设X为无记忆平稳随机过程，Xn表示随机变量的前n个输出。每一个这样的序列对应于实轴［0，1］上的区间［cn，cn+an］。

其中P(xn)表示xn出现的概率。

当p（0）=0.25；p（1）=0.75，对10110编码时如图2所示。

图2 精度描述

最后得出区间为［85/44，367/45］。由此可见越往后其精度越来越大，所以需要有限精度来约束。

2）有限精度推导［6］

有限精度不需要得到长度的精确值，只需满足式（4）可得到唯一解。

根据以上设区间长度an为

即an=0.00..1xxxx，bn表示 an中1前的0的个数，An为N 位整数1xxx..。

当An＜2n-1时，区间上下界相同，最高位可输出。用q位整数表示P(xn)=2-qP(xn)。结合式（2）和式（3）可得：

3 算术编码仿真

3.1 静态模型的M atlab仿真

算术编码的流程如3所示。在输入图像后首先计算其矩阵大小，再统计各个像素的概率，然后在（0，1）上进行编码，从而得出编码的上下限，最后取其中一个元素作为输出结果。解码过程与编码过程相似，利用算术编码的逆作用来锁定区间，进行逐一的推导还原［7～8］。

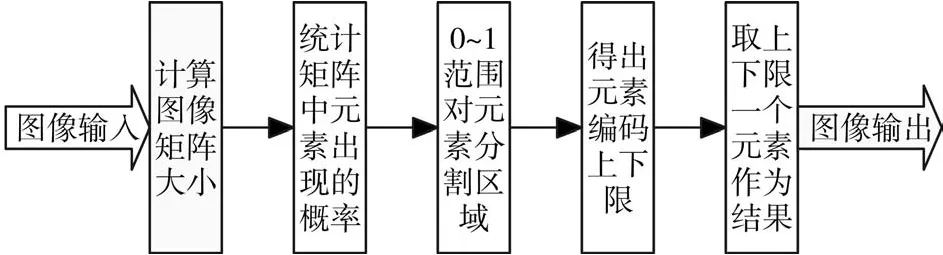
图3 算术编码流程图

图4 为算术编码的压缩图，左边为原始的图像，右边为解压图像，可以看出达到了无损压缩。其编码时间为0.094s算术编码范围上限为0.248453126740064，下限为0.248453061949268。

图4 算术编码压缩图

3.2 自适应模型的M atlab仿真

自适应算术编码在输入图像后首先要建立一个对应的编码模型，也就是上下文建模，对概率进行估计后就可以进行编码，在编码的过程中还要根据输入像素序列来更新概率，直到序列输入完毕即可［9～10］。它的编码流程如图5所示。

图5 自适应算术编码流程图

图6 是自适应算术编码的原文件，图7是对其压缩后的文件，原件的大小为767字节，而压缩后的文件为200字节，压缩率大约为26%，从而在存储中大大减小了数据量，加快了传输速度。图8是解压后的文件，可以看出与原文件相同，实现了无损压缩［11～12］。

图6 自适应编码原图

图7 自适应编码压缩图

图8 自适应编码解压图

4 结语

本文在Matlab中对算术编码的静态模型和自适应模型进行仿真测试，结果表明算术编码的静态模型适合二值图像的压缩，自适应模型比较适合不能预知概率和概率变化的情况，都能实现无损压缩。随着高新技术和电子产业的飞速发展，超大集成电路和CPU的提升，自适应算术编码的运算复杂和精度问题将迎刃而解，使得算术编码将广泛应用于图像视频压缩中。

［1］车晋.数字电视音视频压缩编码技术分析与研究［J］.广播电视信息，2013，18（12）：66-69.

CHE Jin.Analysis and Research of Digital Audio and Vid⁃eo Compression Coding Technology［J］.Radio&Televi⁃sion Information，2013，18（12）：66-69.

［2］曹灿云，王延求.浅仪图像压缩编码技术的发展与应用［J］.信息与电脑，2013，21（3）：127-129.

CAO Canyun，WANG Yanqiu.Development and Applica⁃tion of Image Compression Coding Technology［J］.Com⁃puter&Communication，2013，21（3）：127-129.

［3］邓关宝，杨士元，汪锐.算术编码在图像信号压缩中的应用［J］.计算机工程，2016，32（6）：234-236.

DENG Guanbao，YANG Shiyuan，WAGN Rui.Applica⁃tion of Arithmetic Coding in Image Signal Compression［J］.Computer Engineering，2016，32（6）：234-236.

［4］周晶.图像压缩技术中新型算术编码的研究与应用［J］.自动化与应用，2015，35（4）：47-49.

ZHOU Jin.Research and Application of New Arithmetic Coding in Image Compression［J］.Automation and Appli⁃cation，2015，35（4）：47-49.

［5］张红军，董金明.多媒体数据压缩技术方法研究［J］.忻州师范学院学报，2014，30（2）：20-22.

ZHANG Hongjun，DONG Jinming.Research of Multime⁃dia Data Compression Technology［J］.Journal of Xinzhou Teachers University，2014，30（2）：20-22.

［6］孙倩，岑峰，余有灵.视频压缩中算术编码的研究与发展［J］.高新技术产业发展，2011，10（1）：9-12.

SUN Qian，CEN Feng，YU Youling.Research and Devel⁃opment of Arithmetic Coding in Video Compression［J］.High_tech Industry Development，2011，10（1）：9-12.

［7］韦伟，游彬，万福，等.算术编码理论及误差分析研究［J］.舰船电子工程，2011，32（12）：69-71.

WEI Wei，YOU Bin，WAN Fu，et al.Research of Arithme⁃tic Coding Theory and Error Analysis［J］.Ship Electronic Engineering，2011，32（12）：69-71.

［8］张炜琳，尹聪敏.浅谈算术编码的编解码过程［J］.民营科技，2013，8（12）：8-10.

ZHANG Weilin，YIN Congmin.Discuss of Encoding and Decoding Process of Arithmetic Coding［J］.Private Sci⁃ence and Technology，2013，8（12）：8-10.

［9］李玮，林明.基于自适应算术编码的字符型报文压缩技术［J］.科学技术与工程，2013，13（10）：37-38.

LI Wei，LIN Ming.Character Type Message Compression Technology Based on Adaptive Arithmetic Coding［J］.Sci⁃ence Technology and Engineering，2013，13（10）：37-38.

［10］张丹.基于上下文快速有效的自适应二进制算术编码实现［J］.微型电脑应用，2010，26（7）：56-58.

ZHANG Dan.Implementation of Adaptive Binary Arith⁃metic Coding Based on Context［J］.Microcomputer Ap⁃plications，2010，26（7）：56-58.

［11］韩峥，唐昆，崔慧娟.基于参数模型的自适应二进制算术编码算法［J］.清华大学学报（自然科学版），2009，49（4）：132-534.

HAN Zheng，TANG Kun，CUI Huijuan.Adaptive binary arithmetic coding algorithm based on parameter model［J］.Journal of Tsinghua University（Science and Tech⁃nology），2009，49（4）：132-534.

［12］林德立，蔡建立.基于上下文的自适应二进制算术编码［J］.福建电脑，2009，13（7）：69-70.

LIN Deli，CAI Jianli.Adaptive Binary Arithmetic Coding Based Context［J］.Fujian Computer，2009，13（7）：69-70.

Research of Arithmetic Coding in Image Com pression

WU Xiaoyun
（College of Electronic Information and Electrical Engineering，Shangluo University，Shangluo 726000）

TP391

10.3969/j.issn.1672-9722.2017.09.036

2017年3月9日，

2017年4月20日

商洛学院根植地方专项项目（编号：gz16035）资助。

吴晓云，女，硕士，讲师，研究方向：数据采集与处理，图像处理。